论文笔记之PPO
15年OpenAI发表了TRPO算法,一直策略单调提升的算法;17年DeepMind基于TRPO发表了一篇Distributed-PPO,紧接着OpenAI发表了这篇PPO。可以说TRPO是PPO的前身,PPO在TRPO的基础上进行改进,使得算法可读性更高,实操性更强。
论文地址,点这里
有关TRPO的论文解读,可参考我的另一篇论文笔记之TRPO
PPO作为目前比较火热的model-free类强化学习算法,在许多环境中取得了不错的效果,因此是有必要去学习的。
论文解读参考:
①OpenAI PPO强化学习算法解读
②TRPO和PPO(下)
③强化学习笔记(五)–PPO
④PPO
⑤TRPO与PPO
Note:
- 关于PPO,网上最大的争议点在于是否是Off-policy算法?答:PPO是On-policy算法,虽然其引入了IS因子修正,但是用于采样的策略是旧策略 π o l d \pi_{old} πold(或者说当前策略),然后用这些样本去更新当前策略 θ o l d → θ \theta_{old}\to\theta θold→θ,用来学习并成为最终策略的策略叫目标策略,故采样策略和目标策略都是同一个 θ o l d \theta_{old} θold,因此PPO就是On-policy算法。和DDPG这类算法不同,虽然说从头至尾都用一个网络符号 π θ \pi_\theta πθ来表示策略,但是更新前后是有区别的,DDPG用来更新当前策略的样本来自于经验池,池子里的样本是由许多个之前不同的行为策略产生的,也就是说学习所用的数据“离开”了待学习的目标策略,因此DDPG是Off-policy的。再比如说Q-learning就更明显了,直接摆明有2个策略: g r e e d y greedy greedy和 ϵ − g r e e d y \epsilon-greedy ϵ−greedy策略。因此可以说Off-policy算法一般都会使用IS技术,但使用IS技术的不一定是Off-policy。
- TRPO和PPO都是为了解决策略梯度算法中学习率大小的算法,只不过PPO实现起来更加简便,效果也更好。
- Proximal(近端)个人认为应该指的是策略网络参数的更新是在约束范围内进行,因为有一个范围在,这个范围直觉上感觉很小,所以称之为近端。

- PPO有2个版本:一个是带有可调节的KL因子版本;另一个是带有Clip技术的版本。
Proximal Policy Optimization Algorithms
- Abstract
- 1 Introduction
- 2 Background: Policy Optimization
-
- 2.1 Policy Gradient Methods
- 2.2 Trust Region Methods
- 3 Clipped Surrogate Objective
- 4 Adaptive KL Penalty Coefficient
- 5 Algorithm
- 6 Experiments
-
- 6.1 Comparison of Surrogate Objectives
- 6.2 Comparison to Other Algorithm in the Continuous Domain
- 6.3 Showcase in the Continuous Domain:Humanoid Running and Steering
- 6.4 Comparison to Other Algorithm on the Atari Domain
- 7 Conclusion
Abstract
1 Introduction
略
2 Background: Policy Optimization
2.1 Policy Gradient Methods
PPO和TRPO都是用来解决策略梯度算法中的学习率问题的,因此他们都属于策略梯度算法(PG):
∇ J ( θ ) = E ( s , a ) ∼ ρ π [ ∇ θ log π θ ( a ∣ s ) ⋅ A π θ ( s , a ) ] (1) \nabla J(\theta)=\mathbb{E}_{(s,a)\sim\rho^\pi}[\nabla_\theta\log\pi_\theta(a|s)\cdot A^{\pi_\theta}(s,a)]\tag{1} ∇J(θ)=E(s,a)∼ρπ[∇θlogπθ(a∣s)⋅Aπθ(s,a)](1)
2.2 Trust Region Methods
有关TRPO的论文解读,可参考我的另一篇论文笔记之TRPO。
TRPO的目标函数以及约束为:
m a x i m i z e θ E ( s t , a t ) ∼ ρ π θ o l d [ π θ ( s t , a t ) π θ o l d ( s t , a t ) A π θ o l d ( s t , a t ) ] (3) \mathop{maximize}\limits_{\theta}\mathbb{E}_{(s_t,a_t)\sim\rho^{\pi_{\theta_{old}}}}[\frac{\pi_\theta(s_t,a_t)}{\pi_{\theta_{old}}(s_t,a_t)}A^{\pi_{\theta_{old}}}(s_t,a_t)]\tag{3} θmaximizeE(st,at)∼ρπθold[πθold(st,at)πθ(st,at)Aπθold(st,at)](3) s . t . E ( s t , a t ) ∼ ρ π θ o l d [ K L [ π θ o l d ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ] ] (4) s.t.\,\,\,\mathbb{E}_{(s_t,a_t)\sim\rho^{\pi_{\theta_{old}}}}[KL[\pi_{\theta_{old}}(\cdot|s_t),\pi_\theta(\cdot|s_t)]]\tag{4} s.t.E(st,at)∼ρπθold[KL[πθold(⋅∣st),πθ(⋅∣st)]](4)Note:
- θ o l d \theta_{old} θold指的是当前策略,是即将更新的待更新策略,相对 π θ \pi_\theta πθ而言就是旧策略。
- TRPO对式(3)(4)的优化采用共轭梯度+线性搜索来处理。对式(3)采用一阶近似,对式(4)采用二阶近似。
理论上TRPO开始也是将 K L KL KL散度作为奖惩项的:
m a x i m i z e θ E ( s t , a t ) ∼ ρ π θ o l d [ π θ ( s t , a t ) π θ o l d ( s t , a t ) A π θ o l d ( s t , a t ) − β K L [ π θ o l d ( ⋅ ∣ s t ) , π θ ( ⋅ ∣ s t ) ] ] (5) \mathop{maximize}\limits_{\theta}\mathbb{E}_{(s_t,a_t)\sim\rho^{\pi_{\theta_{old}}}}[\frac{\pi_\theta(s_t,a_t)}{\pi_{\theta_{old}}(s_t,a_t)}A^{\pi_{\theta_{old}}}(s_t,a_t)-\beta KL[\pi_{\theta_{old}}(\cdot|s_t),\pi_{\theta}(\cdot|s_t)]]\tag{5} θmaximizeE(st,at)∼ρπθold[πθold(st,at)πθ(st,at)Aπθold(st,at)−βKL[πθold(⋅∣st),πθ(⋅∣st)]](5)Note:
- 但是在TRPO中 K L KL KL因子是个很小的值,会造成学习缓慢。如果将 β \beta β当做超参数的话,对于不同环境也是难以调节。因此PPO的一个版本就专门设计了可调节的 K L KL KL因子。
- 实验表明,如果采样固定的奖惩因子 β \beta β,并采用 S G D SGD SGD来对式(5)做一阶近似的话,效果是不好的。因此有必要将 β \beta β改成可调节的。
3 Clipped Surrogate Objective
这是PPO的Clip版本。OpenAI的作者提出用Clip技术替代 K L KL KL散度的作用,即限制参数 θ o l d → θ \theta_{old}\to\theta θold→θ步伐过大。
记IS修正因子 r t ( θ ) = π θ ( a t ∣ s t ) π θ o l d ( a t ∣ s t ) r_t(\theta)=\frac{\pi_\theta(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)} rt(θ)=πθold(at∣st)πθ(at∣st)。TRPO优化的目标是一种替代目标,他不直接优化 η θ n e w \eta_{\theta_{new}} ηθnew,而是优化它的一个下界。整个优化过程Kakada称之为CPI(Conservation Policy Iteration),故真正优化的目标函数称之为CPI函数: L C P I ( θ ) = E ( s t , a t ) ∼ ρ π θ o l d [ π θ ( s t , a t ) π θ o l d ( s t , a t ) A π θ o l d ( s t , a t ) ] = E [ r t ( θ ) A π θ o l d ( s t , a t ) ] (6) L^{CPI}(\theta)=\mathbb{E}_{(s_t,a_t)\sim\rho^{\pi_{\theta_{old}}}}[\frac{\pi_\theta(s_t,a_t)}{\pi_{\theta_{old}}(s_t,a_t)}A^{\pi_{\theta_{old}}}(s_t,a_t)]=\mathbb{E}[r_t(\theta)A^{\pi_{\theta_{old}}}(s_t,a_t)]\tag{6} LCPI(θ)=E(st,at)∼ρπθold[πθold(st,at)πθ(st,at)Aπθold(st,at)]=E[rt(θ)Aπθold(st,at)](6)
可以见得,如果不存在一个约束的话, θ o l d → θ \theta_{old}\to\theta θold→θ将会很大,会导致策略提升失效,从而无法解决PG算法的学习率大小问题。
那么PPO的Clip版本的替代函数是什么呢?
PPO的Clip版本的优化的目标也是基于TRPO的优化目标(式(6)),本质上两者都是CPI函数,优化的都是真正回报 η θ n e w \eta_{\theta_{new}} ηθnew的近似。
记Clip超参数 ϵ = 0.2 \epsilon=0.2 ϵ=0.2,则PPO优化目标:
L C L I P ( θ ) = E ( s t , a t ) ∼ ρ π θ o l d [ min { r t ( θ ) A π θ o l d , c l i p ( r t ( θ ) , 1 − ϵ , 1 + ϵ ) A π θ o l d } ] (7) L^{CLIP}(\theta)=\mathbb{E}_{(s_t,a_t)\sim\rho^{\pi_{\theta_{old}}}}[\min\{r_t(\theta)A^{\pi_{\theta_{old}}},clip(r_t(\theta), 1-\epsilon,1+\epsilon)A^{\pi_{\theta_{old}}}\}]\tag{7} LCLIP(θ)=E(st,at)∼ρπθold[min{rt(θ)Aπθold,clip(rt(θ),1−ϵ,1+ϵ)Aπθold}](7)
C l i p Clip Clip目标函数有2大特征:
①用下图即可说明PPO设置 C l i p Clip Clip的意义: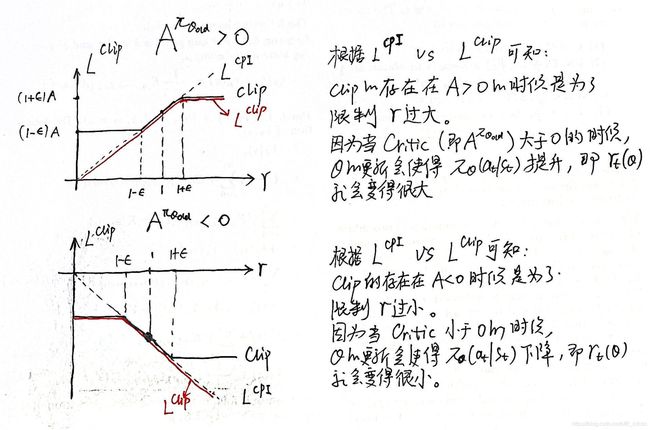 用一句话概括就是 C l i p Clip Clip的存在是为了限制 θ o l d → θ \theta_{old}\to\theta θold→θ更新幅度过大,这个更新方向可能使得 π \pi π是增大的,也可能是减小的,这取决于Critic和0的关系。根据PG理论: A ≥ 0 A\ge0 A≥0,则鼓励 θ \theta θ的更新朝着 π θ \pi_\theta πθ增大的方向移动; A ≤ 0 A\leq0 A≤0,则鼓励 θ \theta θ的更新朝着 π θ \pi_\theta πθ减小的方向移动。
用一句话概括就是 C l i p Clip Clip的存在是为了限制 θ o l d → θ \theta_{old}\to\theta θold→θ更新幅度过大,这个更新方向可能使得 π \pi π是增大的,也可能是减小的,这取决于Critic和0的关系。根据PG理论: A ≥ 0 A\ge0 A≥0,则鼓励 θ \theta θ的更新朝着 π θ \pi_\theta πθ增大的方向移动; A ≤ 0 A\leq0 A≤0,则鼓励 θ \theta θ的更新朝着 π θ \pi_\theta πθ减小的方向移动。
Note:
- 虽然理论上说 K L KL KL散度优化目的是让2个分布输出的动作概率一致,而非策略参数一致。但是实际上对于2个不同参数的分布,要做到对于状态空间 S \mathcal{S} S的每一个状态都对应的概率密度(离散下为概率)相等,是很难的,如下图所示:
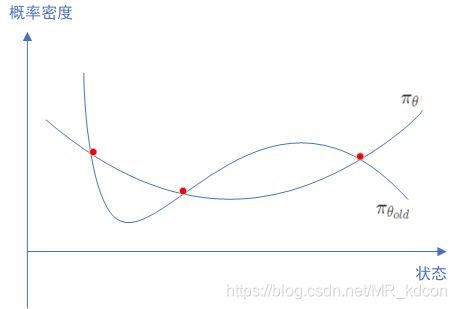 因此 m i n i m i z e θ K L ( π θ o l d ( ⋅ ∣ s ) ∣ ∣ π θ ( ⋅ ∣ s ) ) \mathop{minimize}\limits_\theta KL(\pi_{\theta_{old}}(\cdot|s)||\pi_\theta(\cdot|s)) θminimizeKL(πθold(⋅∣s)∣∣πθ(⋅∣s))的结果往往是 θ o l d ≈ θ \theta_{old}\approx\theta θold≈θ。因此无论是 K L KL KL散度还是 C l i p Clip Clip,其优化的结果就是使2个策略的参数趋于一致。
因此 m i n i m i z e θ K L ( π θ o l d ( ⋅ ∣ s ) ∣ ∣ π θ ( ⋅ ∣ s ) ) \mathop{minimize}\limits_\theta KL(\pi_{\theta_{old}}(\cdot|s)||\pi_\theta(\cdot|s)) θminimizeKL(πθold(⋅∣s)∣∣πθ(⋅∣s))的结果往往是 θ o l d ≈ θ \theta_{old}\approx\theta θold≈θ。因此无论是 K L KL KL散度还是 C l i p Clip Clip,其优化的结果就是使2个策略的参数趋于一致。 - 通过 C l i p Clip Clip技术限制住 r ( θ ) r(\theta) r(θ)一来可以保证策略提升不会失效;二来可以保证IS处理后的方差不会过大从而保证IS的有效性。
②: L C L I P L^{CLIP} LCLIP可作为选取目标函数的一个保守的下界。如下图所示: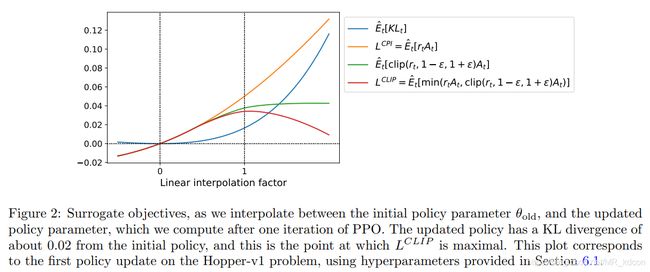 图中横坐标可以理解为参数从开始更新到更新完毕的过程。纵坐标为 K L ( θ o l d ∣ ∣ θ ) KL(\theta_{old}||\theta) KL(θold∣∣θ)值。从图中可看出以 L C L I P L^{CLIP} LCLIP为目标对于参数更新步伐的控制较强,更新“保守”。
图中横坐标可以理解为参数从开始更新到更新完毕的过程。纵坐标为 K L ( θ o l d ∣ ∣ θ ) KL(\theta_{old}||\theta) KL(θold∣∣θ)值。从图中可看出以 L C L I P L^{CLIP} LCLIP为目标对于参数更新步伐的控制较强,更新“保守”。
4 Adaptive KL Penalty Coefficient
第三节讲述了PPO的 C l i p Clip Clip版本,这一节讲述PPO的另一个版本——采用可调节的 K L KL KL散度因子。
算法的大致步骤为:
 Note:
Note:
- 算法涉及3个超参数: β 、 d t a r g 、 ( 1.5 , 2 ) \beta、d_{targ}、(1.5,2) β、dtarg、(1.5,2),但这三者的敏感性很低,调节并不是很麻烦。
- 效果比 L C L I P L^{CLIP} LCLIP要差,但是可作为一个baseline。
- 采用SGD做一阶优化。
5 Algorithm
回顾一下:第三节介绍了基于TRPO的 L C L I P L^{CLIP} LCLIP算法;第四节介绍了基于TRPO的 L K L P E N L^{KLPEN} LKLPEN算法。这一节开始介绍完整的PPO算法。
PPO算法的完整目标函数:
L t C L I P + V F + S ( θ ) = E ( s t , a t ) ∼ ρ π θ o l d [ L t C L I P ( θ ) − c 1 L t V F ( θ ) + c 2 S [ π θ ] ( s t ) ] (9) L_t^{CLIP+VF+S}(\theta)=\mathbb{E}_{(s_t,a_t)\sim\rho^{\pi_{\theta_{old}}}}[L_t^{CLIP}(\theta)-c_1L_t^{VF}(\theta)+c_2S[\pi_\theta](s_t)]\tag{9} LtCLIP+VF+S(θ)=E(st,at)∼ρπθold[LtCLIP(θ)−c1LtVF(θ)+c2S[πθ](st)](9)Note:
- c 1 , c 2 c_1,c_2 c1,c2为2个超参数, S S S为信息熵增加探索率, L t V F L_t^{VF} LtVF为训练Critic网络 V θ V_\theta Vθ的损失函数。
- 这里采用 L C L I P L^{CLIP} LCLIP作为替代函数。
优势函数的估计基于以下式子:
A t = − V ( s t ) + [ r t + γ t + 1 + ⋯ + γ T − t − 1 r T − 1 + γ T − t V ( s T ) ] (10) A_t=-V(s_t)+[r_t+\gamma_{t+1}+\cdots+\gamma^{T-t-1}r_{T-1}+\gamma^{T-t}V(s_T)]\tag{10} At=−V(st)+[rt+γt+1+⋯+γT−t−1rT−1+γT−tV(sT)](10)Note:
- 式(10)第一部分的 V V V通过价值网络得到, V V V网络的训练遵从: m i n i m i z e θ E ( s t , a t ) ∼ ρ π θ o l d [ 1 2 ( V θ ( s t ) − V t t a r g ( s t ) ) 2 ] \mathop{minimize}\limits_\theta\mathbb{E}_{(s_t,a_t)\sim\rho^{\pi_{\theta_{old}}}}[\frac{1}{2}(V_\theta(s_t)-V_t^{targ}(s_t))^2] θminimizeE(st,at)∼ρπθold[21(Vθ(st)−Vttarg(st))2]
- 式(10)的第二部分是一个T步的 Q Q Q,它通过MC采样结果相加可得。
- PPO算法拥有Actor-Critic算法的框架。
- 算法中分成了 N N N个Actor去做T步的探索,一共收集 N ∗ T N*T N∗T个样本,然后进行训练过程中,采集 M ≤ N T M\leq NT M≤NT个样本做mini-batch,更新 θ o l d → θ \theta_{old}\to\theta θold→θ。从这里就可以看出PPO是如何利用样本训练的以及PPO是一个On-policy算法,因为目标策略 θ o l d \theta_{old} θold的更新和行为策略 θ o l d \theta_{old} θold是同一个。
- PPO的训练中T步是固定的长度,其值远小于一个episode的长度。
- PPO的自动调节 K L KL KL因子版本伪代码如下:

6 Experiments
6.1 Comparison of Surrogate Objectives
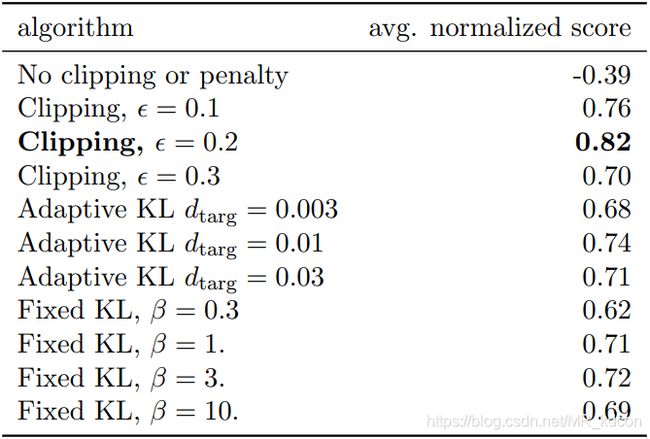
这一小节用于对比三种替代目标函数 L C P I 、 L C L I P 、 L K L P E N L^{CPI}、L^{CLIP}、L^{KLPEN} LCPI、LCLIP、LKLPEN,其中 L K L P E N L^{KLPEN} LKLPEN还包括固定和自动调节的 β \beta β。
实验设置:
-
超参数:除了 c l i p clip clip版本有专属的 ϵ \epsilon ϵ,奖惩 K L KL KL版本有专属的 ( β , d t a r g ) (\beta,d_{targ}) (β,dtarg),其余都一样的设置:
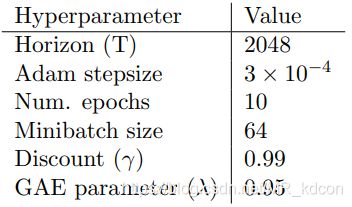
-
网络设置:用神经网络来表示策略。
-
其他:实验环境来自于OpenAI-Gym的Mujoco仿真模拟器。一共涉及7种环境,每种环境设置3个随机种子。评价指标为7*3=21个结果的平均值。
- 从实验结果来看, L C L I P L^{CLIP} LCLIP版本的表现要较好于其他三种。
- 显然失去了参数更新限制的 L C P I L^{CPI} LCPI表现拉跨,因为参数 θ o l d → θ \theta_{old}\to\theta θold→θ不设限,导致策略提升失效以及IS修正失效。
6.2 Comparison to Other Algorithm in the Continuous Domain
这一小节是将PPO算法与其他算法在同一环境是的比较。
上一轮胜出的是 c l i p clip clip版本的PPO,所以这一节拿 c l i p clip clip版本的PPO与其余5种算法对比,实验结果如下: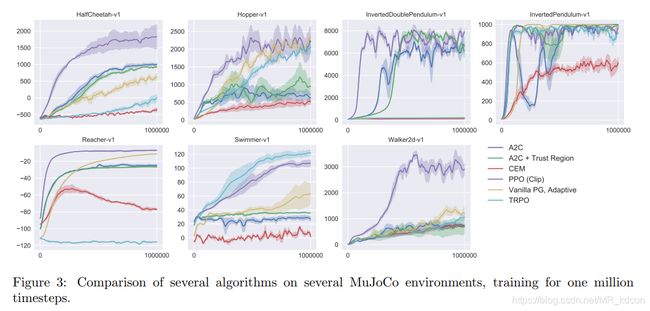 从实验结果来看,显然PPO的表现力要好于其余5位。
从实验结果来看,显然PPO的表现力要好于其余5位。
6.3 Showcase in the Continuous Domain:Humanoid Running and Steering
这一节是测试PPO(自动调节 β \beta β版本)在高维连续动作空间环境Humanoid上的表现效果。实验分三种难度,从低到高分别是:①RoboschoolHumanoid-v0②RoboschoolHumanoidFlagrun-v0③RoboschoolHumanoidFlagrunHarder
实验所涉及到的超参数如下:
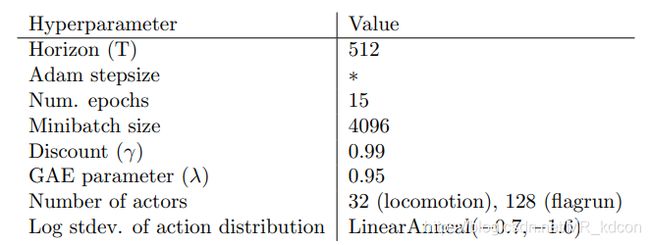
实验效果图如下:

实验结果如下:
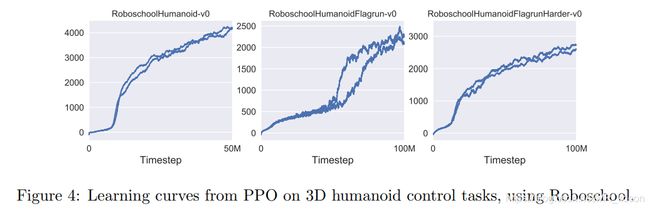
从实验结果来看,PPO在高维连续空间task的表现力还是不错的,面对高维task的时候,PPO是一个不错的baseline。
6.4 Comparison to Other Algorithm on the Atari Domain
这一节测试的是PPO算法和其余2种算法A2C、ACER在Atari环境中的表现对比。
一共测试49种Atari游戏。PPO的超参数如下: 其余2种算法的超参数已经调节到最好效果了。
其余2种算法的超参数已经调节到最好效果了。
实验分2个评价指标,评价值是49局游戏里获胜的次数,实验结果如下:

从实验结果来看,PPO在Atari领域还是可行的一种算法。
7 Conclusion
- PPO是一种Policy-based方法。
- PPO是一种
On-policy的随机策略算法。 - PPO=(Policy-Gradient)+(Importance-Sampling)+(KL散度),即它的目标函数基于PG,然后利用IS技术提高采样效率,同时为了避免IS中前后策略相差太大而引入 K L KL KL散度。和TRPO不同的是,PPO的KL散度是作为奖惩项放在目标函数中的,并且引入自动调节的 K L KL KL因子 β \beta β。
- PPO也可以理解成PPO=(TRPO-constraint)+(clip)=(TRPO-constraint)+(adaptive- β \beta β),即PPO是一种基于TRPO且有2个版本的RL算法。
- 为了降低 K L KL KL散度计算的复杂度,PPO引入 C l i p Clip Clip技术将 ( θ o l d , θ ) (\theta_{old},\theta) (θold,θ)限定在一定范围内。
- TRPO对约束使用了二阶近似,而PPO只使用了一阶,并弃用了难度较大的共轭梯度以及线性搜索算法,故PPO更易实现且效果更好。
- 可用于作为一个较为保守的替代目标。一般来说,CPI函数和CLIP函数都是对真正目标 η \eta η的近似。