模拟信号数字化的过程（二）——编码（以脉冲编码调制为例）

---

前言

量化后的信号已经是离散的多电平数字信号，下一步的问题是如何将这个多电平数字信号用二进制符号表示。将多电平信号转化为二进制信号的过程称为编码。

---

一、PCM是什么？

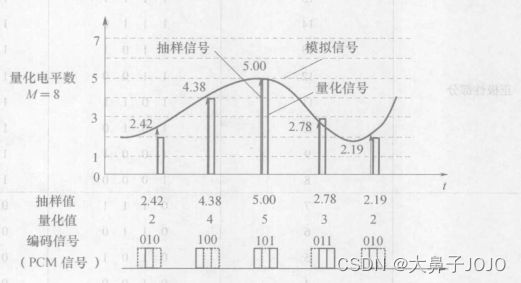
在图中给出了模拟信号数字化过程——“抽样、量化和编码”的示例。图中,模拟信号的抽样值为2.42,4.38,5.00,2,78和2.19。若按照“四舍五入”的原则量化为整数值,则抽样值量化后变为2,4,5,3和2。在按照二进制数编码后,量化值(quantizedvalue)就变成二进制符号:010、100、101 、011和010。
上述将模拟信号变换成二进制信号的方法称为脉冲编码调制(PCM)。这种编码技术于20世纪40年代已经在通信技术中采用了。由于当时是从信号调制的观点研究这种技术的,所以称为脉冲编码调制。目前,它不仅用于通信领域,还广泛应用于计算机、遥控遥测、数字仪表等许多领域。在这些领域中,常将其称为模拟/数字(A/D)变换

以上描述来源于樊昌信老师主编的《通信原理（第七版）》，概括的说，所谓脉冲编码调制（PCM），不只是一种量化的手段，而应该描述成一种数字调制手段，即一种将模拟信号通过采样、量化和编码后变成数字信号从而得以在数字信道中进行传播的一种手段。一个PCM系统的原理图如图所示：

二、PCM中常用的编码过程

在了解编码过程时要首先明确，编码过程是在采样和量化已经完成的基础上进行的，即需要进行编码的值已经是量化过后的离散值。

1.自然码

自然码即按照二进制的自然规律排列而成的编码，通常采用我们熟知的8421BCD码，如将量化值0编码成0000，将量化值15编码成1111，在确定量化范围后，编码位数也很容易确定。

2.折叠码

样值脉冲极性	量化极序号	折叠二进制码
正极性部分	15	1111
正极性部分	14	1110
正极性部分	13	1101
正极性部分	12	1100
正极性部分	11	1011
正极性部分	10	1010
正极性部分	09	1001
正极性部分	08	1000
负极性部分	07	0000
负极性部分	06	0001
负极性部分	05	0010
负极性部分	04	0011
负极性部分	03	0100
负极性部分	02	0101
负极性部分	01	0110
负极性部分	00	0111

---

上表中为折叠二进制码的编码规律，之所以称其为折叠码，是因为其正极性部分与负极性部分存在明显的折叠关系（又称映像关系）。
所谓折叠关系是指：其正极性部分和负极性部分存在除符号位外，其他各位呈映像关系。
因此折叠码在用最高位表示极性后，双极性电压可以采用单极性编码方式来处理，这就使编码电路和编码过程大大简化。
折叠码的另外一个优点如下引用部分所示：

折叠码的另一个优点是误码对于小电压的影响较小。例如,若有一个码组为“1000”,在传输或处理时发生一个符号错误,变成“0000”。从表中可见,若它为自然码,则它所代表的量化级将从8变成0,误差为8;若它为折叠码,则它将从8变成7,误差为1。但是,若一个码组从“1111”错成“0111”,则自然码将从15变成7,误差仍为8;而折叠码则将从15错成为0,误差增大为15。这表明,折叠码对于小信号有利。由于语音信号小电压出现的概率较大,所以折叠码有利于减小语音信号的平均量化噪声。
————摘自樊昌信《通信原理（第七版）》

3、常用的PCM编码思路–A律13折线PCM编码

在A律13折线PCM编码中，由于正负各8段，每段内有16个量化极，因此总共需要$2\times 8\times 16=256=2^8$个量化极，因此需要编码的位数为8位，如下所示：
$C_1$:极性码，正极性为1，负极性为0；
$C_2、C_3、C_4$:段落码，表示样值幅度所处的段落。
$C_5、C_6、C_7、C_8$:段内码，其16种可能状态对应16个量化极。
编码器根据样值的幅度所在的段落和量化极，编出相应的幅度码。

三、脉冲编码调制MATLAB仿真实例

PCM编码函数：

 function code=PCMcoding(S)
    z=sign(S);                                %判断S的正负
    MaxS=max(abs(S));                         %求S的最大值 
    S=abs(S/MaxS);                            %归一化
    Q=2048*S;                                 %量化
    code=zeros(length(S),8);                  %代码存储矩阵（全零）
    
    % 段落码判断程序
    for i=1:length(S)
        if (Q(i)>=128)&&(Q(i)<=2048)
            code(i,2)=1;            %在第五段与第八段之间，段位码第一位都为"1"
        end
        if (Q(i)>32)&&(Q(i)<128)||(Q(i)>=512)&&(Q(i)<=2048)
            code(i,3)=1;            %在第三四七八段内，段位码第二位为"1"
        end
        if (Q(i)>=16)&&(Q(i)<32)||(Q(i)>=64)&&(Q(i)<128)||(Q(i)>=256)&&(Q(i)<512)||(Q(i)>=1024)&&(Q(i)<=2048)
            code(i,4)=1;            %在二四六八段内，段位码第三位为"1"
        end
    end
    
    N=zeros(length(S));                              %段内码判断程序
    
    for i=1:length(S)
        N(i)=bin2dec(num2str(code(i,2:4)))+1;        %找到code位于第几段
    end
    
    a=[0,16,32,64,128,256,512,1024];                 %量化间隔
    b=[1,1,2,4,8,16,32,64];                          %除以16，得到每段的最小量化间隔
    for i=1:length(S)  
        q=ceil((Q(i)-a(N(i)))/b(N(i)));              %求出在段内的位置
        if q==0
            code(i,(5:8))=[0,0,0,0];                 %如果输入为零则输出"0"
        else k=num2str(dec2bin(q-1,4));              %编码段内码为二进制
            code(i,5)=str2num(k(1));
            code(i,6)=str2num(k(2));
            code(i,7)=str2num(k(3));
            code(i,8)=str2num(k(4));
        end
        if z(i)>0
            code(i,1)=1;
        elseif z(i)<0
            code(i,1)=0;
        end                                           %符号位的判断
    end
    code = reshape(code', 1, []);
end

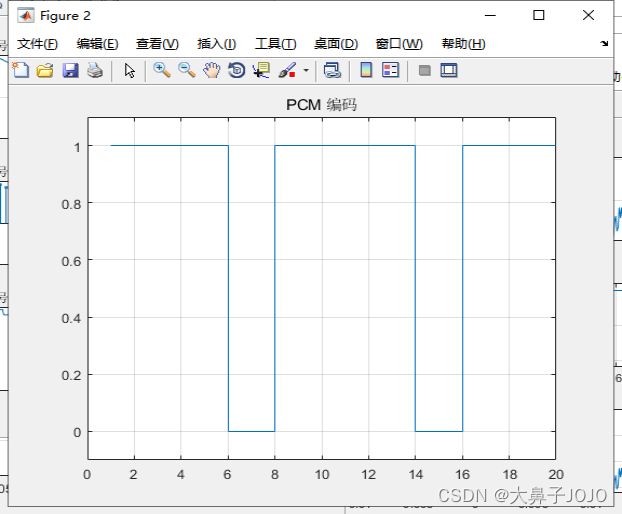
PCM编码函数调用方式：

pcm_encode = PCMcoding(xt);
figure(2)
stairs(pcm_encode);
axis([0 20 -0.1 1.1]);
title('PCM 编码');
grid on;

结果如图所示（接上篇博客量化信号）

PCM解码：

function s=PCMdecoding(encode, max)
    encode=(reshape(encode',8,length(encode)/8))';
    l=size(encode,1);
    a=[0,16,32,64,128,256,512,1024];
    b=[1 1 2 4 8 16 32 64];
    c=[0 1.5:15.5];
    for i=1:l
        x=encode(i,1);
        T=bin2dec(num2str(encode(i,(2:4))))+1;
        Y=bin2dec(num2str(encode(i,(5:8))));
        if Y==0
            k(i)=a(T)/2048;
        else
            k(i)=(a(T)+b(T)*c(Y))/2048;
        end
        if x==0
            s(i)=-k(i);
        else
            s(i)=k(i);
        end
    end
    s = s*max;
end

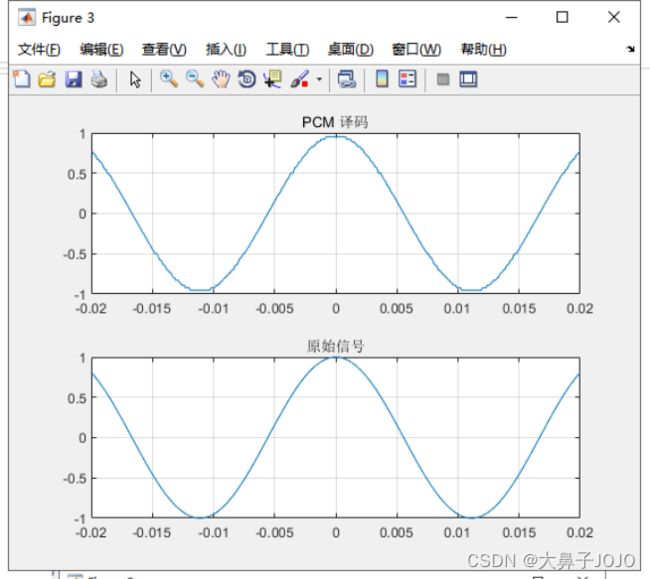
PCM译码函数的调用方式

%PCM 译码
pcm_decode = PCMdecoding(pcm_encode, max);
figure(3)
subplot(2,1,1);plot(t, pcm_decode);
title('PCM 译码');grid on;
subplot(2,1,2);plot(t,xt);
title('原始信号');grid on;

这里再次声明，PCM是一种将模拟信号经过采样，量化，编码转换为数字信号的一种调制方式，而非只是一种编码方式，其采用的是二进制编码方式，

四、总结

本篇文章和与上一篇一起简单分析了模拟信号的数字化过程，数字化是模拟世界通往数字世界的桥梁，即波的传输方式可以从模拟调制（AM,FM,PM）等发展到数字调制（数字基带调制，2ASK,2FSK,2PSK）等，从而大大发展了通信系统，为近几年数字通信系统的高速发展打下了基础。