BP神经网络的搭建
1. BP神经网络的简介和结构参数
神经网络是机器学习中一种常见的数学模型，通过构建类似于大脑神经突触联接的结构，来进行信息处理。在应用神经网络的过程中，处理信息的单元一般分为三类：输入单元、输出单元和隐含单元。 顾名思义：输入单元接受外部给的信号与数据；输出单元实现系统处理结果的输出；隐含单元处在输入和输出单元之间，从网络系统外部是无法观测到隐含单元的结构的。除了上述三个处理信息的单元之外，神经元间的连接强度大小由权值等参数来决定。
1.1 BP神经网络的结构组成
下图是训练神经网络时经常出现的一个界面，从这部分我们可以看到，这是一个2输入1输出，8个隐含层的BP网络，称为2-8-1网络结构
1.2 BP神经网络训练界面的参数解读
需要注意的是：
1. 泛化性：表示BP神经网络在训练过程中，如果均方误差（MSE）连续6次不降反升，则网络停止训练。
2. 误差精度：关于mu参数含义的一种理解是，mu是误差精度参数，用于给神经网络的权重再加一个调制，这样可以避免在BP网络训练的过程中陷入局部最小值，mu的范围为0到1。
2. 实现BP网络的步骤
- 读取数据
- 设置训练数据和预测数据
- 训练样本数据归一化
- 构建BP神经网络
- 网络参数配置(训练次数，学习速率，训练目标最小误差.等)
- BP神经网络训练
- 测试样本归一化
- BP神经网络预测
- 预测结果反归一化与误差计算
- 验证集的真实值与预测值误差比较
首先以这个最简单是前馈神经网络为例子：
1.前馈
前馈代表了所有的信息都从输入 经过某些中间的计算而最终输出到
，而不存在从模型的输出到输入的反馈(feedback），对于有反馈的情况即为循环神经网络(recurrent neural network)前馈网络已经广泛应用在工业界，其重要性不言而喻，而且它也是理解在自然语言处理中应用广泛的循环神经网络的基础。
2.网络
而网络则代表了该模型是将不同的基本函数组合在一起形成的模型。
例如通过将三个函数
串联起来构成最终的函数 
，
就是网络的第一层，
就是网络的第二层，以此类推。这个链的长度又被称作网络的深度（depth)，深度学习也因此得名。
而前馈网络的最后一层被称作输出层(output layer)，对于我们的训练数据，每一个输入 
都有相应的标记 
，而网络的输出层的结果需要尽量接近 。
但对于其它层来说，和训练数据没有这样的直接对应关系，即我们的算法只要求最后的输出接近于真实的标记，而对于中间每层的目的并没有明确定义，所以这些层又被称作隐藏层(hidden layer)。
3.神经
神经代表了它的灵感部分受到了神经科学的影响。每一隐藏层通常是矢量值，而这些隐藏层的维度定义了网络的宽度。我们可以将每层看做从一个大的从矢量到矢量的函数映射，但从另一方面也可以将矢量的每个元素看做一个小的神经元，每个神经元进行了矢量到标量的映射操作（这一操作又被称作激活函数，activation function），而每一层是不同的神经元并行运算的综合。
前馈神经网络是
1.读取数据
%%简单的前馈神经网络
x = [0 1 2 3 4 5 6 7 8]; %初始数据输入,x坐标值
t = [0 0.84 0.91 0.14 -0.77 -0.96 -0.28 0.66 0.99];%输出，y坐标值
plot(x,t,'o') %x，y值一一对应运行结果如下：
2.构建前馈型神经网络
net = feedforwardnet(10);%前馈型神经网络
net = configure(net,x,t);% 配置网络输入和输出,以达到最好的匹配输入和目标数据.
y1 = net(x)
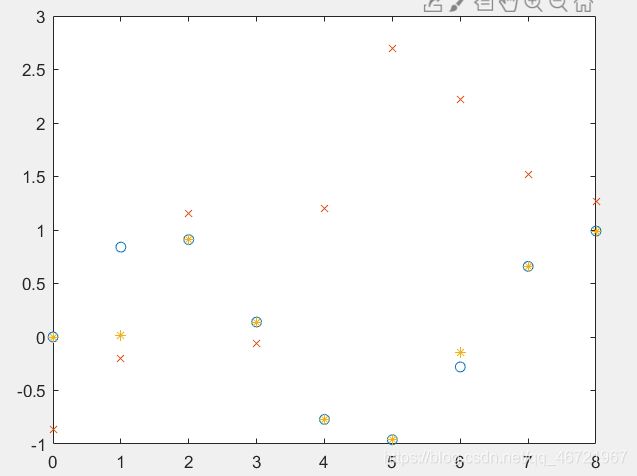
plot(x,t,'o',x,y1,'x')
3.训练网络
net = train(net,x,t);
y2 = net(x)
plot(x,t,'o',x,y1,'x',x,y2,'*')
