别被打脸

NNDL 实验七循环神经网络（3）LSTM的记忆能力实验

文章目录

前言

一、6.3 LSTM的记忆能力实验

6.3.1 模型构建

6.3.1.1 LSTM层

6.3.1.2 模型汇总

6.3.2 模型训练

6.3.2.1 训练指定长度的数字预测模型

6.3.2.2 多组训练

6.3.2.3 损失曲线展示

【思考题1】LSTM与SRN实验结果对比，谈谈看法。（选做）

6.3.3 模型评价

6.3.3.1 在测试集上进行模型评价

6.3.3.2 模型在不同长度的数据集上的准确率变化图

【思考题2】LSTM与SRN在不同长度数据集上的准确度对比，谈谈看法。（选做）

6.3.3.3 LSTM模型门状态和单元状态的变化

【思考题3】分析LSTM中单元状态和门数值的变化图，并用自己的话解释该图。

总结

前言

首先，我这次写的还是很细，这次感觉学到了很多，像LSTM的原理以及LSTM计算过程的推导，这个是很重要的。

其次，是这两天做了好多抗原，希望疫情快点过去吧，河大加油。

最后，写的不太好，希望老师和各位大佬多教教我。

使用LSTM模型重新进行数字求和实验，验证LSTM模型的长程依赖能力。

一、6.3 LSTM的记忆能力实验

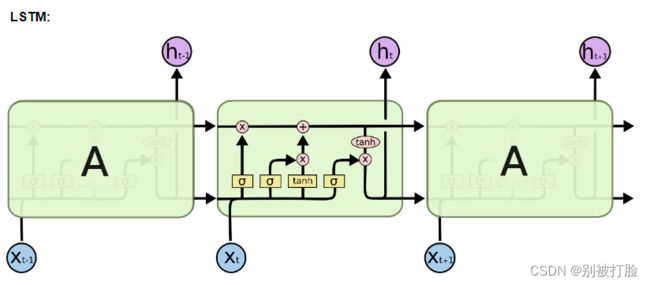
具体计算分为三步：

（1）计算三个“门”

（2）计算内部状态

（3）计算输出状态

通过学习这些门的设置，LSTM可以选择性地忽略或者强化当前的记忆或是输入信息，帮助网络更好地学习长句子的语义信息。

在本节中，我们使用LSTM模型重新进行数字求和实验，验证LSTM模型的长程依赖能力。

6.3.1 模型构建

在本实验中，我们将使用第6.1.2.4节中定义Model_RNN4SeqClass模型，并构建 LSTM 算子．只需要实例化 LSTM 算，并传入Model_RNN4SeqClass模型，就可以用 LSTM 进行数字求和实验

6.3.1.1 LSTM层

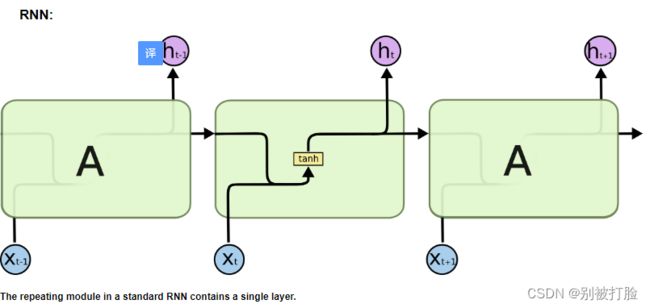
LSTM层的代码与SRN层结构相似，只是在SRN层的基础上增加了内部状态、输入门、遗忘门和输出门的定义和计算。这里LSTM层的输出也依然为序列的最后一个位置的隐状态向量。代码实现如下：

# coding=gbk
import torch.nn.functional as F
import torch.nn as nn
import torch

# 声明LSTM和相关参数
class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, Wi_attr=None, Wf_attr=None, Wo_attr=None, Wc_attr=None,
                 Ui_attr=None, Uf_attr=None, Uo_attr=None, Uc_attr=None, bi_attr=None, bf_attr=None,
                 bo_attr=None, bc_attr=None):
        super(LSTM, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size

        # 初始化模型参数
        if Wi_attr==None:
            self.W_i=torch.zeros(size=[input_size, hidden_size],dtype=torch.float32)
            self.W_i=torch.nn.Parameter(self.W_i)
        else:
            self.W_i=torch.nn.Parameter(Wi_attr)
        if Wf_attr==None:
            self.W_f = torch.zeros(size=[input_size, hidden_size], dtype=torch.float32)
            self.W_f = torch.nn.Parameter(self.W_f)
        else:
            self.W_f = torch.nn.Parameter(Wf_attr)
        if Wo_attr==None:
            self.W_o = torch.zeros(size=[input_size, hidden_size], dtype=torch.float32)
            self.W_o = torch.nn.Parameter(self.W_o)
        else:
            self.W_o = torch.nn.Parameter(Wo_attr)
        if Wc_attr==None:
            self.W_c = torch.zeros(size=[input_size, hidden_size], dtype=torch.float32)
            self.W_c = torch.nn.Parameter(self.W_c)
        else:
            self.W_c = torch.nn.Parameter(Wc_attr)
        if Ui_attr==None:
            self.U_i = torch.zeros(size=[hidden_size, hidden_size], dtype=torch.float32)
            self.U_i = torch.nn.Parameter(self.U_i)
        else:
            self.U_i = torch.nn.Parameter(Ui_attr)
        if Uf_attr==None:
            self.U_f = torch.zeros(size=[hidden_size, hidden_size], dtype=torch.float32)
            self.U_f = torch.nn.Parameter(self.U_f)
        else:
            self.U_f = torch.nn.Parameter(Uf_attr)
        if Uo_attr==None:
            self.U_o = torch.zeros(size=[hidden_size, hidden_size], dtype=torch.float32)
            self.U_o = torch.nn.Parameter(self.U_o)
        else:
            self.U_o = torch.nn.Parameter(Uo_attr)
        if Uc_attr==None:
            self.U_c = torch.zeros(size=[hidden_size, hidden_size], dtype=torch.float32)
            self.U_c = torch.nn.Parameter(self.U_c)
        else:
            self.U_c = torch.nn.Parameter(Uc_attr)
        if bi_attr==None:
            self.b_i = torch.zeros(size=[1, hidden_size], dtype=torch.float32)
            self.b_i = torch.nn.Parameter(self.b_i)
        else:
            self.b_i = torch.nn.Parameter(bi_attr)
        if bf_attr==None:
            self.b_f = torch.zeros(size=[1, hidden_size], dtype=torch.float32)
            self.b_f = torch.nn.Parameter(self.b_f)
        else:
            self.b_f = torch.nn.Parameter(bf_attr)
        if bo_attr==None:
            self.b_o = torch.zeros(size=[1, hidden_size], dtype=torch.float32)
            self.b_o = torch.nn.Parameter(self.b_o)
        else:
            self.b_o = torch.nn.Parameter(bo_attr)
        if bc_attr==None:
            self.b_c = torch.zeros(size=[1, hidden_size], dtype=torch.float32)
            self.b_c = torch.nn.Parameter(self.b_c)
        else:
            self.b_c = torch.nn.Parameter(bc_attr)


    # 初始化状态向量和隐状态向量
    def init_state(self, batch_size):
        hidden_state = torch.zeros(size=[batch_size, self.hidden_size], dtype=torch.float32)
        cell_state = torch.zeros(size=[batch_size, self.hidden_size], dtype=torch.float32)
        return hidden_state, cell_state

    # 定义前向计算
    def forward(self, inputs, states=None):
        # inputs: 输入数据，其shape为batch_size x seq_len x input_size
        batch_size, seq_len, input_size = inputs.shape

        # 初始化起始的单元状态和隐状态向量，其shape为batch_size x hidden_size
        if states is None:
            states = self.init_state(batch_size)
        hidden_state, cell_state = states

        # 执行LSTM计算，包括：输入门、遗忘门和输出门、候选内部状态、内部状态和隐状态向量
        for step in range(seq_len):
            # 获取当前时刻的输入数据step_input: 其shape为batch_size x input_size
            step_input = inputs[:, step, :]
            # 计算输入门, 遗忘门和输出门, 其shape为：batch_size x hidden_size
            I_gate = F.sigmoid(torch.matmul(step_input, self.W_i) + torch.matmul(hidden_state, self.U_i) + self.b_i)
            F_gate = F.sigmoid(torch.matmul(step_input, self.W_f) + torch.matmul(hidden_state, self.U_f) + self.b_f)
            O_gate = F.sigmoid(torch.matmul(step_input, self.W_o) + torch.matmul(hidden_state, self.U_o) + self.b_o)
            # 计算候选状态向量, 其shape为：batch_size x hidden_size
            C_tilde = F.tanh(torch.matmul(step_input, self.W_c) + torch.matmul(hidden_state, self.U_c) + self.b_c)
            # 计算单元状态向量, 其shape为：batch_size x hidden_size
            cell_state = F_gate * cell_state + I_gate * C_tilde
            # 计算隐状态向量，其shape为：batch_size x hidden_size
            hidden_state = O_gate * F.tanh(cell_state)

        return hidden_state

Wi_attr = torch.tensor([[0.1, 0.2], [0.1, 0.2]])
Wf_attr = torch.tensor([[0.1, 0.2], [0.1, 0.2]])
Wo_attr = torch.tensor([[0.1, 0.2], [0.1, 0.2]])
Wc_attr = torch.tensor([[0.1, 0.2], [0.1, 0.2]])
Ui_attr = torch.tensor([[0.0, 0.1], [0.1, 0.0]])
Uf_attr = torch.tensor([[0.0, 0.1], [0.1, 0.0]])
Uo_attr = torch.tensor([[0.0, 0.1], [0.1, 0.0]])
Uc_attr = torch.tensor([[0.0, 0.1], [0.1, 0.0]])
bi_attr = torch.tensor([[0.1, 0.1]])
bf_attr = torch.tensor([[0.1, 0.1]])
bo_attr = torch.tensor([[0.1, 0.1]])
bc_attr = torch.tensor([[0.1, 0.1]])

lstm = LSTM(2, 2, Wi_attr=Wi_attr, Wf_attr=Wf_attr, Wo_attr=Wo_attr, Wc_attr=Wc_attr,
                 Ui_attr=Ui_attr, Uf_attr=Uf_attr, Uo_attr=Uo_attr, Uc_attr=Uc_attr,
                 bi_attr=bi_attr, bf_attr=bf_attr, bo_attr=bo_attr, bc_attr=bc_attr)

inputs = torch.tensor([[[1, 0]]], dtype=torch.float32)
hidden_state = lstm(inputs)
print(hidden_state)

运行结果为：

tensor([[0.0594, 0.0952]], grad_fn=)

pytorch框架已经内置了LSTM的API torch.nn.LSTM，其与自己实现的SRN不同点在于其实现时采用了两个偏置，同时矩阵相乘时参数在输入数据前面，如下公式所示：

这里我们可以将自己实现的SRN和Paddle框架内置的SRN返回的结果进行打印展示，实现代码如下。

# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size = 8, 20, 32
inputs = torch.randn(size=[batch_size, seq_len, input_size])

# 设置模型的hidden_size
hidden_size = 32
paddle_lstm = nn.LSTM(input_size, hidden_size)
self_lstm = LSTM(input_size, hidden_size)

self_hidden_state = self_lstm(inputs)
paddle_outputs, (paddle_hidden_state, paddle_cell_state) = paddle_lstm(inputs)

print("self_lstm hidden_state: ", self_hidden_state.shape)
print("paddle_lstm outpus:", paddle_outputs.shape)
print("paddle_lstm hidden_state:", paddle_hidden_state.shape)
print("paddle_lstm cell_state:", paddle_cell_state.shape)

运行结果为：

self_lstm hidden_state: torch.Size([8, 32])
paddle_lstm outpus: torch.Size([8, 20, 32])
paddle_lstm hidden_state: torch.Size([1, 20, 32])
paddle_lstm cell_state: torch.Size([1, 20, 32])

可以看到，自己实现的LSTM由于没有考虑多层因素，因此没有层次这个维度，因此其输出shape为[8, 32]。同时由于在以上代码使用Paddle内置API实例化LSTM时，默认定义的是1层的单向SRN，因此其shape为[1, 8, 32]，同时隐状态向量为[8,20, 32].

接下来，我们可以将自己实现的LSTM与Paddle内置的LSTM在输出值的精度上进行对比，这里首先根据Paddle内置的LSTM实例化模型（为了进行对比，在实例化时只保留一个偏置，将偏置bihbih设置为0），然后提取该模型对应的参数，进行参数分割后，使用相应参数去初始化自己实现的LSTM，从而保证两者在参数初始化时是一致的。

在进行实验时，首先定义输入数据inputs，然后将该数据分别传入Paddle内置的LSTM与自己实现的LSTM模型中，最后通过对比两者的隐状态输出向量。代码实现如下：

import torch
torch.manual_seed(0)

# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size, hidden_size = 2, 5, 10, 10
inputs = torch.randn(size=[batch_size, seq_len, input_size])

# 设置模型的hidden_size
bih_attr = torch.nn.Parameter(torch.zeros([4*hidden_size, ]))
paddle_lstm = nn.LSTM(input_size, hidden_size)
paddle_lstm.bias_ih_l0=bih_attr
paddle_lstm.bias_ih_l1=bih_attr
paddle_lstm.bias_ih_l2=bih_attr
paddle_lstm.bias_ih_l3=bih_attr
paddle_lstm.bias_ih_l4=bih_attr

# 获取paddle_lstm中的参数，并设置相应的paramAttr,用于初始化lstm
print(paddle_lstm.weight_ih_l0.T.shape)
chunked_W = torch.split(paddle_lstm.weight_ih_l0.T, split_size_or_sections=10, dim=-1)
chunked_U = torch.split(paddle_lstm.weight_hh_l0.T, split_size_or_sections=10, dim=-1)
chunked_b = torch.split(paddle_lstm.bias_hh_l0.T, split_size_or_sections=10, dim=-1)
print(chunked_b[0].shape,chunked_b[1].shape,chunked_b[2].shape)
Wi_attr = torch.tensor(chunked_W[0])
Wf_attr = torch.tensor(chunked_W[1])
Wc_attr = torch.tensor(chunked_W[2])
Wo_attr = torch.tensor(chunked_W[3])
Ui_attr = torch.tensor(chunked_U[0])
Uf_attr = torch.tensor(chunked_U[1])
Uc_attr = torch.tensor(chunked_U[2])
Uo_attr = torch.tensor(chunked_U[3])
bi_attr = torch.tensor(chunked_b[0])
bf_attr = torch.tensor(chunked_b[1])
bc_attr = torch.tensor(chunked_b[2])
bo_attr = torch.tensor(chunked_b[3])
self_lstm = LSTM(input_size, hidden_size, Wi_attr=Wi_attr, Wf_attr=Wf_attr, Wo_attr=Wo_attr, Wc_attr=Wc_attr,
                 Ui_attr=Ui_attr, Uf_attr=Uf_attr, Uo_attr=Uo_attr, Uc_attr=Uc_attr,
                 bi_attr=bi_attr, bf_attr=bf_attr, bo_attr=bo_attr, bc_attr=bc_attr)

# 进行前向计算，获取隐状态向量，并打印展示
self_hidden_state = self_lstm(inputs)
paddle_outputs, (paddle_hidden_state, _) = paddle_lstm(inputs)
print("paddle SRN:\n", paddle_hidden_state.detach().numpy().squeeze(0))
print("self SRN:\n", self_hidden_state.detach().numpy())

运行结果为：

paddle SRN:
[[ 0.06057303 0.0352371 -0.04730584 0.16420795 0.13122755 -0.15738934
0.1771467 -0.00439037 -0.02465727 -0.3045934 ]
[ 0.14093119 0.11173882 0.27511147 0.04056947 -0.00766448 -0.16597556
0.32193324 0.01466936 -0.28634343 -0.19916353]
[ 0.14699097 0.03865489 -0.11907008 0.24300049 0.31992295 -0.07868578
0.19904399 0.03308991 0.09627407 -0.1424047 ]
[ 0.06207867 0.2342088 0.00657276 0.1791542 0.32928583 -0.04207081
-0.06663163 -0.00604617 -0.10334547 0.10602648]
[ 0.05457556 0.05111036 -0.10710873 0.00312713 -0.09948594 -0.11760624
0.11195059 0.13914587 -0.09120954 -0.1052993 ]]
self SRN:
[[ 0.0940564 -0.14659543 -0.14954016 0.20936163 -0.12826967 0.14749622
0.00946941 0.1993472 -0.06859784 -0.2767597 ]
[ 0.17217153 0.16705877 -0.05719084 0.14882174 0.10330292 -0.20432511
0.13150844 0.03508793 -0.07331903 -0.06966008]]

可以看到，两者的输出基本是一致的。另外，还可以进行对比两者在运算速度方面的差异。代码实现如下：

import time

# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size = 8, 20, 32
inputs = torch.randn(size=[batch_size, seq_len, input_size])

# 设置模型的hidden_size
hidden_size = 32
self_lstm = LSTM(input_size, hidden_size)
paddle_lstm = nn.LSTM(input_size, hidden_size)

# 计算自己实现的SRN运算速度
model_time = 0
for i in range(100):
    strat_time = time.time()
    hidden_state = self_lstm(inputs)
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    end_time = time.time()
    model_time += (end_time - strat_time)
avg_model_time = model_time / 90
print('self_lstm speed:', avg_model_time, 's')

# 计算Paddle内置的SRN运算速度
model_time = 0
for i in range(100):
    strat_time = time.time()
    outputs, (hidden_state, cell_state) = paddle_lstm(inputs)
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    end_time = time.time()
    model_time += (end_time - strat_time)
avg_model_time = model_time / 90
print('paddle_lstm speed:', avg_model_time, 's')

运行结果为：

self_lstm speed: 0.006990869839986165 s
paddle_lstm speed: 0.00160928832160102 s

可以看到，由于pytorch框架的LSTM底层采用了C++实现并进行优化，Paddle框架内置的LSTM运行效率远远高于自己实现的LSTM。

6.3.1.2 模型汇总

在本节实验中，我们将使用6.1.2.4的Model_RNN4SeqClass作为预测模型，不同在于在实例化时将传入实例化的LSTM层。

6.3.2 模型训练

6.3.2.1 训练指定长度的数字预测模型

本节将基于RunnerV3类进行训练，首先定义模型训练的超参数，并保证和简单循环网络的超参数一致. 然后定义一个train函数，其可以通过指定长度的数据集，并进行训练. 在train函数中，首先加载长度为length的数据，然后实例化各项组件并创建对应的Runner，然后训练该Runner。同时在本节将使用4.5.4节定义的准确度（Accuracy）作为评估指标，代码实现如下：

import os
import random
import torch
import numpy as np
from nndl import RunnerV3
from nndl import Accuracy, RunnerV3


# 训练轮次
num_epochs = 500
# 学习率
lr = 0.001
# 输入数字的类别数
num_digits = 10
# 将数字映射为向量的维度
input_size = 32
# 隐状态向量的维度
hidden_size = 32
# 预测数字的类别数
num_classes = 19
# 批大小
batch_size = 8
# 模型保存目录
save_dir = "./checkpoints"

# 可以设置不同的length进行不同长度数据的预测实验
def train(length):
    print(f"\n====> Training LSTM with data of length {length}.")
    np.random.seed(0)
    random.seed(0)
    torch.manual_seed(0)

    # 加载长度为length的数据
    data_path = f"./datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    train_set, dev_set, test_set = DigitSumDataset(train_examples), DigitSumDataset(dev_examples), DigitSumDataset(test_examples)
    train_loader = torch.utils.data.DataLoader(train_set, batch_size=batch_size)
    dev_loader = torch.utils.data.DataLoader(dev_set, batch_size=batch_size)
    test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)
    # 实例化模型
    base_model = LSTM(input_size, hidden_size)
    model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
    # 指定优化器
    optimizer = torch.optim.Adam(lr=lr, params=model.parameters())
    # 定义评价指标
    metric = Accuracy()
    # 定义损失函数
    loss_fn = torch.nn.CrossEntropyLoss()
    # 基于以上组件，实例化Runner
    runner = RunnerV3(model, optimizer, loss_fn, metric)

    # 进行模型训练
    model_save_path = os.path.join(save_dir, f"best_lstm_model_{length}.pdparams")
    runner.train(train_loader, dev_loader, num_epochs=num_epochs, eval_steps=100, log_steps=100, save_path=model_save_path)

    return runner

用到的函数为：

from torch.nn.init import xavier_uniform

class Embedding(nn.Module):
    def __init__(self, num_embeddings, embedding_dim,
                 para_attr=xavier_uniform):
        super(Embedding, self).__init__()
        # 定义嵌入矩阵
        W=torch.zeros(size=[num_embeddings, embedding_dim], dtype=torch.float32)
        self.W = torch.nn.Parameter(W)
        xavier_uniform(W)
    def forward(self, inputs):
        # 根据索引获取对应词向量
        embs = self.W[inputs]
        return embs

# 基于RNN实现数字预测的模型
class Model_RNN4SeqClass(nn.Module):
    def __init__(self, model, num_digits, input_size, hidden_size, num_classes):
        super(Model_RNN4SeqClass, self).__init__()
        # 传入实例化的RNN层，例如SRN
        self.rnn_model = model
        # 词典大小
        self.num_digits = num_digits
        # 嵌入向量的维度
        self.input_size = input_size
        # 定义Embedding层
        self.embedding = Embedding(num_digits, input_size)
        # 定义线性层
        self.linear = nn.Linear(hidden_size, num_classes)

    def forward(self, inputs):
        # 将数字序列映射为相应向量
        inputs_emb = self.embedding(inputs)
        # 调用RNN模型
        hidden_state = self.rnn_model(inputs_emb)
        # 使用最后一个时刻的状态进行数字预测
        logits = self.linear(hidden_state)
        return logits

from torch.utils.data import Dataset

class DigitSumDataset(Dataset):
    def __init__(self, data):
        self.data = data

    def __getitem__(self, idx):
        example = self.data[idx]
        seq = torch.tensor(example[0], dtype=torch.int64)
        label = torch.tensor(example[1], dtype=torch.int64)
        return seq, label

    def __len__(self):
        return len(self.data)

# 加载数据
def load_data(data_path):
    # 加载训练集
    train_examples = []
    train_path = os.path.join(data_path, "train.txt")
    with open(train_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            train_examples.append((seq, label))

    # 加载验证集
    dev_examples = []
    dev_path = os.path.join(data_path, "dev.txt")
    with open(dev_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            dev_examples.append((seq, label))

    # 加载测试集
    test_examples = []
    test_path = os.path.join(data_path, "test.txt")
    with open(test_path, "r", encoding="utf-8") as f:
        for line in f.readlines():
            # 解析一行数据，将其处理为数字序列seq和标签label
            items = line.strip().split("\t")
            seq = [int(i) for i in items[0].split(" ")]
            label = int(items[1])
            test_examples.append((seq, label))

    return train_examples, dev_examples, test_examples

6.3.2.2 多组训练

接下来，分别进行数据长度为10, 15, 20, 25, 30, 35的数字预测模型训练实验，训练后的runner保存至runners字典中。

lstm_runners = {}

lengths = [10, 15, 20, 25, 30, 35]
for length in lengths:
    runner = train(length)
    lstm_runners[length] = runner

运行结果为：

====> Training LSTM with data of length 10.

[Evaluate] dev score: 0.09000, dev loss: 2.86460
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.09000
[Train] epoch: 5/500, step: 200/19000, loss: 2.48144
[Evaluate] dev score: 0.10000, dev loss: 2.84022
[Evaluate] best accuracy performence has been updated: 0.09000 --> 0.10000
[Train] epoch: 7/500, step: 300/19000, loss: 2.46724
[Evaluate] dev score: 0.10000, dev loss: 2.83455
[Train] epoch: 10/500, step: 400/19000, loss: 2.41858
[Evaluate] dev score: 0.10000, dev loss: 2.83207
[Train] epoch: 13/500, step: 500/19000, loss: 2.45705
[Evaluate] dev score: 0.76000, dev loss: 1.38295
[Train] epoch: 484/500, step: 18400/19000, loss: 0.00069
[Evaluate] dev score: 0.76000, dev loss: 1.38330
[Train] epoch: 486/500, step: 18500/19000, loss: 0.00040
[Evaluate] dev score: 0.77000, dev loss: 1.38700
[Evaluate] best accuracy performence has been updated: 0.76000 --> 0.77000
[Train] epoch: 489/500, step: 18600/19000, loss: 0.00067
[Evaluate] dev score: 0.77000, dev loss: 1.38891
[Train] epoch: 492/500, step: 18700/19000, loss: 0.00050
[Evaluate] dev score: 0.77000, dev loss: 1.39004
[Train] epoch: 494/500, step: 18800/19000, loss: 0.00053
[Evaluate] dev score: 0.77000, dev loss: 1.39317
[Train] epoch: 497/500, step: 18900/19000, loss: 0.00069
[Evaluate] dev score: 0.77000, dev loss: 1.39381
[Evaluate] dev score: 0.77000, dev loss: 1.39583
[Train] Training done!

====> Training LSTM with data of length 15.
[Train] epoch: 0/500, step: 0/19000, loss: 2.83505
[Train] epoch: 2/500, step: 100/19000, loss: 2.78581
[Evaluate] dev score: 0.07000, dev loss: 2.86551
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.07000
[Train] epoch: 5/500, step: 200/19000, loss: 2.49482
[Evaluate] dev score: 0.10000, dev loss: 2.84367
[Evaluate] best accuracy performence has been updated: 0.07000 --> 0.10000
[Train] epoch: 7/500, step: 300/19000, loss: 2.48387
[Evaluate] dev score: 0.10000, dev loss: 2.83747
[Train] epoch: 10/500, step: 400/19000, loss: 2.40902
[Evaluate] best accuracy performence has been updated: 0.79000 --> 0.80000
[Train] epoch: 418/500, step: 15900/19000, loss: 0.00319
[Evaluate] dev score: 0.80000, dev loss: 1.25397
[Train] epoch: 421/500, step: 16000/19000, loss: 0.00458
[Evaluate] dev score: 0.80000, dev loss: 1.25535
[Train] epoch: 423/500, step: 16100/19000, loss: 0.00265
[Evaluate] dev score: 0.80000, dev loss: 1.25759
[Train] epoch: 426/500, step: 16200/19000, loss: 0.00167
[Evaluate] dev score: 0.80000, dev loss: 1.25949
[Train] epoch: 428/500, step: 16300/19000, loss: 0.00092
[Evaluate] dev score: 0.80000, dev loss: 1.26127
[Train] epoch: 431/500, step: 16400/19000, loss: 0.00161
[Evaluate] dev score: 0.80000, dev loss: 1.26405
[Train] epoch: 434/500, step: 16500/19000, loss: 0.00154
[Evaluate] dev score: 0.80000, dev loss: 1.26565
[Train] epoch: 436/500, step: 16600/19000, loss: 0.00068
[Evaluate] dev score: 0.80000, dev loss: 1.26796
[Train] epoch: 439/500, step: 16700/19000, loss: 0.00132
[Evaluate] dev score: 0.80000, dev loss: 1.27097
[Train] epoch: 442/500, step: 16800/19000, loss: 0.00164
[Evaluate] dev score: 0.80000, dev loss: 1.27273
[Train] epoch: 444/500, step: 16900/19000, loss: 0.00087
[Evaluate] dev score: 0.80000, dev loss: 1.27552
[Train] epoch: 447/500, step: 17000/19000, loss: 0.00130
[Evaluate] dev score: 0.80000, dev loss: 1.27835
[Train] epoch: 450/500, step: 17100/19000, loss: 0.00409
[Evaluate] dev score: 0.80000, dev loss: 1.28007
[Train] epoch: 452/500, step: 17200/19000, loss: 0.00074
[Evaluate] dev score: 0.80000, dev loss: 1.28351
[Train] epoch: 455/500, step: 17300/19000, loss: 0.00037
[Evaluate] dev score: 0.80000, dev loss: 1.28587
[Train] epoch: 457/500, step: 17400/19000, loss: 0.00081
[Evaluate] dev score: 0.80000, dev loss: 1.28809
[Train] epoch: 460/500, step: 17500/19000, loss: 0.00078
[Evaluate] dev score: 0.80000, dev loss: 1.29226
[Train] epoch: 463/500, step: 17600/19000, loss: 0.00063
[Evaluate] dev score: 0.80000, dev loss: 1.29375
[Train] epoch: 465/500, step: 17700/19000, loss: 0.00081
[Evaluate] dev score: 0.80000, dev loss: 1.29866
[Train] epoch: 468/500, step: 17800/19000, loss: 0.00133
[Evaluate] dev score: 0.80000, dev loss: 1.30044
[Train] epoch: 471/500, step: 17900/19000, loss: 0.00188
[Evaluate] dev score: 0.80000, dev loss: 1.30269
[Train] epoch: 473/500, step: 18000/19000, loss: 0.00104
[Evaluate] dev score: 0.80000, dev loss: 1.30722
[Train] epoch: 476/500, step: 18100/19000, loss: 0.00080
[Evaluate] dev score: 0.80000, dev loss: 1.30969
[Train] epoch: 478/500, step: 18200/19000, loss: 0.00039
[Evaluate] dev score: 0.80000, dev loss: 1.31293
[Train] epoch: 481/500, step: 18300/19000, loss: 0.00066
[Evaluate] dev score: 0.80000, dev loss: 1.31794
[Train] epoch: 484/500, step: 18400/19000, loss: 0.00054
[Evaluate] dev score: 0.80000, dev loss: 1.31867
[Train] epoch: 486/500, step: 18500/19000, loss: 0.00031
[Evaluate] dev score: 0.80000, dev loss: 1.32285
[Train] epoch: 489/500, step: 18600/19000, loss: 0.00053
[Evaluate] dev score: 0.80000, dev loss: 1.32626
[Train] epoch: 492/500, step: 18700/19000, loss: 0.00063
[Evaluate] dev score: 0.80000, dev loss: 1.32818
[Train] epoch: 494/500, step: 18800/19000, loss: 0.00034
[Evaluate] dev score: 0.80000, dev loss: 1.33328
[Train] epoch: 497/500, step: 18900/19000, loss: 0.00036
[Evaluate] dev score: 0.80000, dev loss: 1.33515
[Evaluate] dev score: 0.80000, dev loss: 1.33826
[Train] Training done!

====> Training LSTM with data of length 20.
[Train] epoch: 0/500, step: 0/19000, loss: 2.83505
[Train] epoch: 2/500, step: 100/19000, loss: 2.76947
[Evaluate] dev score: 0.10000, dev loss: 2.85964
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.10000
[Train] epoch: 5/500, step: 200/19000, loss: 2.48617
[Evaluate] dev score: 0.10000, dev loss: 2.83813
[Train] epoch: 7/500, step: 300/19000, loss: 2.48167
[Evaluate] dev score: 0.10000, dev loss: 2.83235
[Train] epoch: 10/500, step: 400/19000, loss: 2.40573
[Evaluate] dev score: 0.10000, dev loss: 2.82994
[Train] epoch: 13/500, step: 500/19000, loss: 2.46062
[Evaluate] dev score: 0.10000, dev loss: 2.82841
[Train] epoch: 15/500, step: 600/19000, loss: 2.36476
[Evaluate] dev score: 0.10000, dev loss: 2.82848
[Train] epoch: 18/500, step: 700/19000, loss: 2.50661
[Evaluate] dev score: 0.10000, dev loss: 2.82729
[Train] epoch: 21/500, step: 800/19000, loss: 2.69739
[Evaluate] dev score: 0.10000, dev loss: 2.82654
[Train] epoch: 23/500, step: 900/19000, loss: 2.67164
[Evaluate] dev score: 0.10000, dev loss: 2.82587
[Train] epoch: 26/500, step: 1000/19000, loss: 2.73424
[Evaluate] dev score: 0.11000, dev loss: 2.82421
[Evaluate] best accuracy performence has been updated: 0.10000 --> 0.11000
[Train] epoch: 28/500, step: 1100/19000, loss: 3.44213
[Evaluate] dev score: 0.12000, dev loss: 2.82406
[Evaluate] best accuracy performence has been updated: 0.11000 --> 0.12000
[Train] epoch: 31/500, step: 1200/19000, loss: 2.81749

[Evaluate] dev score: 0.72000, dev loss: 1.76485
[Evaluate] best accuracy performence has been updated: 0.71000 --> 0.72000
[Train] epoch: 352/500, step: 13400/19000, loss: 0.00286
[Evaluate] dev score: 0.73000, dev loss: 1.77673
[Evaluate] best accuracy performence has been updated: 0.72000 --> 0.73000
[Train] epoch: 355/500, step: 13500/19000, loss: 0.03924
[Evaluate] dev score: 0.73000, dev loss: 1.77541
[Train] epoch: 357/500, step: 13600/19000, loss: 0.01049
[Evaluate] dev score: 0.73000, dev loss: 1.77870
[Train] epoch: 360/500, step: 13700/19000, loss: 0.01205
[Evaluate] dev score: 0.73000, dev loss: 1.78517
[Train] epoch: 363/500, step: 13800/19000, loss: 0.00505
[Evaluate] dev score: 0.73000, dev loss: 1.78481
[Train] epoch: 365/500, step: 13900/19000, loss: 0.00416
[Evaluate] dev score: 0.73000, dev loss: 1.78524
[Train] epoch: 368/500, step: 14000/19000, loss: 0.00970
[Evaluate] dev score: 0.73000, dev loss: 1.78913
[Train] epoch: 371/500, step: 14100/19000, loss: 0.00992
[Evaluate] dev score: 0.73000, dev loss: 1.78916
[Train] epoch: 373/500, step: 14200/19000, loss: 0.03927
[Evaluate] dev score: 0.73000, dev loss: 1.79077
[Train] epoch: 376/500, step: 14300/19000, loss: 0.01398
[Evaluate] dev score: 0.72000, dev loss: 1.79417
[Train] epoch: 378/500, step: 14400/19000, loss: 0.01049
[Evaluate] dev score: 0.72000, dev loss: 1.79497
[Train] epoch: 381/500, step: 14500/19000, loss: 0.01269
[Evaluate] dev score: 0.72000, dev loss: 1.79722
[Train] epoch: 384/500, step: 14600/19000, loss: 0.01123
[Evaluate] dev score: 0.72000, dev loss: 1.79931
[Train] epoch: 386/500, step: 14700/19000, loss: 0.00823
[Evaluate] dev score: 0.72000, dev loss: 1.80139
[Train] epoch: 389/500, step: 14800/19000, loss: 0.00241
[Evaluate] dev score: 0.72000, dev loss: 1.80689
[Train] epoch: 392/500, step: 14900/19000, loss: 0.02594
[Evaluate] dev score: 0.72000, dev loss: 1.80951
[Train] epoch: 394/500, step: 15000/19000, loss: 0.01275
[Evaluate] dev score: 0.72000, dev loss: 1.81205
[Train] epoch: 397/500, step: 15100/19000, loss: 0.00252
[Evaluate] dev score: 0.72000, dev loss: 1.81857
[Train] epoch: 400/500, step: 15200/19000, loss: 0.03170
[Evaluate] dev score: 0.72000, dev loss: 1.81997
[Train] epoch: 402/500, step: 15300/19000, loss: 0.00160
[Evaluate] dev score: 0.72000, dev loss: 1.82440
[Train] epoch: 405/500, step: 15400/19000, loss: 0.00837
[Evaluate] dev score: 0.72000, dev loss: 1.82802
[Train] epoch: 407/500, step: 15500/19000, loss: 0.00461
[Evaluate] dev score: 0.72000, dev loss: 1.82951
[Train] epoch: 410/500, step: 15600/19000, loss: 0.00497
[Evaluate] dev score: 0.72000, dev loss: 1.83551
[Train] epoch: 413/500, step: 15700/19000, loss: 0.00222
[Evaluate] dev score: 0.72000, dev loss: 1.83732
[Train] epoch: 415/500, step: 15800/19000, loss: 0.00176
[Evaluate] dev score: 0.72000, dev loss: 1.84012
[Train] epoch: 418/500, step: 15900/19000, loss: 0.00433
[Evaluate] dev score: 0.72000, dev loss: 1.84767
[Train] epoch: 421/500, step: 16000/19000, loss: 0.00421
[Evaluate] dev score: 0.71000, dev loss: 1.85009
[Train] epoch: 423/500, step: 16100/19000, loss: 0.01154
[Evaluate] dev score: 0.71000, dev loss: 1.85613
[Train] epoch: 426/500, step: 16200/19000, loss: 0.00394
[Evaluate] dev score: 0.71000, dev loss: 1.86571
[Train] epoch: 428/500, step: 16300/19000, loss: 0.00451
[Evaluate] dev score: 0.71000, dev loss: 1.86908
[Train] epoch: 431/500, step: 16400/19000, loss: 0.00580
[Evaluate] dev score: 0.71000, dev loss: 1.87763
[Train] epoch: 434/500, step: 16500/19000, loss: 0.00293
[Evaluate] dev score: 0.71000, dev loss: 1.88435
[Train] epoch: 436/500, step: 16600/19000, loss: 0.00434
[Evaluate] dev score: 0.71000, dev loss: 1.88968
[Train] epoch: 439/500, step: 16700/19000, loss: 0.00134
[Evaluate] dev score: 0.71000, dev loss: 1.89978
[Train] epoch: 442/500, step: 16800/19000, loss: 0.00893
[Evaluate] dev score: 0.71000, dev loss: 1.90282
[Train] epoch: 444/500, step: 16900/19000, loss: 0.00361
[Evaluate] dev score: 0.71000, dev loss: 1.90847
[Train] epoch: 447/500, step: 17000/19000, loss: 0.00119
[Evaluate] dev score: 0.70000, dev loss: 1.91738
[Train] epoch: 450/500, step: 17100/19000, loss: 0.01069
[Evaluate] dev score: 0.70000, dev loss: 1.91850
[Train] epoch: 452/500, step: 17200/19000, loss: 0.00080
[Evaluate] dev score: 0.70000, dev loss: 1.92626
[Train] epoch: 455/500, step: 17300/19000, loss: 0.00269
[Evaluate] dev score: 0.70000, dev loss: 1.93184
[Train] epoch: 457/500, step: 17400/19000, loss: 0.00176
[Evaluate] dev score: 0.71000, dev loss: 1.93430
[Train] epoch: 460/500, step: 17500/19000, loss: 0.00212
[Evaluate] dev score: 0.71000, dev loss: 1.94325
[Train] epoch: 463/500, step: 17600/19000, loss: 0.00098
[Evaluate] dev score: 0.71000, dev loss: 1.94598
[Train] epoch: 465/500, step: 17700/19000, loss: 0.00076
[Evaluate] dev score: 0.71000, dev loss: 1.95027
[Train] epoch: 468/500, step: 17800/19000, loss: 0.00193
[Evaluate] dev score: 0.71000, dev loss: 1.95995
[Train] epoch: 471/500, step: 17900/19000, loss: 0.00128
[Evaluate] dev score: 0.71000, dev loss: 1.95994
[Train] epoch: 473/500, step: 18000/19000, loss: 0.00349
[Evaluate] dev score: 0.71000, dev loss: 1.96585
[Train] epoch: 476/500, step: 18100/19000, loss: 0.00139
[Evaluate] dev score: 0.71000, dev loss: 1.97238
[Train] epoch: 478/500, step: 18200/19000, loss: 0.00186
[Evaluate] dev score: 0.71000, dev loss: 1.97150
[Train] epoch: 481/500, step: 18300/19000, loss: 0.00246
[Evaluate] dev score: 0.71000, dev loss: 1.97660
[Train] epoch: 484/500, step: 18400/19000, loss: 0.00103
[Evaluate] dev score: 0.71000, dev loss: 1.97730
[Train] epoch: 486/500, step: 18500/19000, loss: 0.00174
[Evaluate] dev score: 0.71000, dev loss: 1.97380
[Train] epoch: 489/500, step: 18600/19000, loss: 0.00062
[Evaluate] dev score: 0.71000, dev loss: 1.97653
[Train] epoch: 492/500, step: 18700/19000, loss: 0.00298
[Evaluate] dev score: 0.71000, dev loss: 1.97168
[Train] epoch: 494/500, step: 18800/19000, loss: 0.00130
[Evaluate] dev score: 0.71000, dev loss: 1.97103
[Train] epoch: 497/500, step: 18900/19000, loss: 0.00053
[Evaluate] dev score: 0.71000, dev loss: 1.97714
[Evaluate] dev score: 0.71000, dev loss: 1.97366
[Train] Training done!

====> Training LSTM with data of length 25.
[Train] epoch: 0/500, step: 0/19000, loss: 2.83505
[Train] epoch: 2/500, step: 100/19000, loss: 2.77655
[Evaluate] dev score: 0.10000, dev loss: 2.86074
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.10000
[Train] epoch: 5/500, step: 200/19000, loss: 2.49976
[Evaluate] dev score: 0.10000, dev loss: 2.84144
[Train] epoch: 7/500, step: 300/19000, loss: 2.49110
[Evaluate] dev score: 0.10000, dev loss: 2.83578
[Train] epoch: 10/500, step: 400/19000, loss: 2.41369
[Evaluate] dev score: 0.10000, dev loss: 2.83335
[Train] epoch: 13/500, step: 500/19000, loss: 2.46401
[Evaluate] dev score: 0.10000, dev loss: 2.83232
[Train] epoch: 15/500, step: 600/19000, loss: 2.38640
[Evaluate] dev score: 0.10000, dev loss: 2.83254
[Train] epoch: 18/500, step: 700/19000, loss: 2.51424

[Evaluate] dev score: 0.40000, dev loss: 3.61628
[Evaluate] best accuracy performence has been updated: 0.38000 --> 0.40000
[Train] epoch: 394/500, step: 15000/19000, loss: 0.08060
[Evaluate] dev score: 0.36000, dev loss: 3.71179
[Train] epoch: 397/500, step: 15100/19000, loss: 0.04139
[Evaluate] dev score: 0.35000, dev loss: 3.81133
[Train] epoch: 400/500, step: 15200/19000, loss: 0.19323
[Evaluate] dev score: 0.37000, dev loss: 3.83067
[Train] epoch: 402/500, step: 15300/19000, loss: 0.03759
[Evaluate] dev score: 0.35000, dev loss: 3.85875
[Train] epoch: 405/500, step: 15400/19000, loss: 0.01963
[Evaluate] dev score: 0.36000, dev loss: 3.86882
[Train] epoch: 407/500, step: 15500/19000, loss: 0.03708
[Evaluate] dev score: 0.35000, dev loss: 3.88566
[Train] epoch: 410/500, step: 15600/19000, loss: 0.03960
[Evaluate] dev score: 0.36000, dev loss: 3.90958
[Train] epoch: 413/500, step: 15700/19000, loss: 0.01620
[Evaluate] dev score: 0.36000, dev loss: 3.92829
[Train] epoch: 415/500, step: 15800/19000, loss: 0.02653
[Evaluate] dev score: 0.36000, dev loss: 3.95439
[Train] epoch: 418/500, step: 15900/19000, loss: 0.01211
[Evaluate] dev score: 0.36000, dev loss: 3.96535
[Train] epoch: 421/500, step: 16000/19000, loss: 0.02010
[Evaluate] dev score: 0.36000, dev loss: 3.98574
[Train] epoch: 423/500, step: 16100/19000, loss: 0.01403
[Evaluate] dev score: 0.36000, dev loss: 4.00418
[Train] epoch: 426/500, step: 16200/19000, loss: 0.10261
[Evaluate] dev score: 0.33000, dev loss: 3.87917
[Train] epoch: 428/500, step: 16300/19000, loss: 0.50658
[Evaluate] dev score: 0.24000, dev loss: 4.19479
[Train] epoch: 431/500, step: 16400/19000, loss: 0.77854
[Evaluate] dev score: 0.37000, dev loss: 3.88633
[Train] epoch: 434/500, step: 16500/19000, loss: 0.05411
[Evaluate] dev score: 0.32000, dev loss: 4.37722
[Train] epoch: 436/500, step: 16600/19000, loss: 0.04985
[Evaluate] dev score: 0.35000, dev loss: 3.95593
[Train] epoch: 439/500, step: 16700/19000, loss: 0.04037
[Evaluate] dev score: 0.36000, dev loss: 4.05939
[Train] epoch: 442/500, step: 16800/19000, loss: 0.06667
[Evaluate] dev score: 0.37000, dev loss: 4.01447
[Train] epoch: 444/500, step: 16900/19000, loss: 0.03957
[Evaluate] dev score: 0.37000, dev loss: 4.12112
[Train] epoch: 447/500, step: 17000/19000, loss: 0.03272
[Evaluate] dev score: 0.34000, dev loss: 4.04134
[Train] epoch: 450/500, step: 17100/19000, loss: 0.13312
[Evaluate] dev score: 0.33000, dev loss: 4.29661
[Train] epoch: 452/500, step: 17200/19000, loss: 0.07697
[Evaluate] dev score: 0.32000, dev loss: 4.34585
[Train] epoch: 455/500, step: 17300/19000, loss: 0.01970
[Evaluate] dev score: 0.32000, dev loss: 4.23175
[Train] epoch: 457/500, step: 17400/19000, loss: 0.02952
[Evaluate] dev score: 0.34000, dev loss: 4.00266
[Train] epoch: 460/500, step: 17500/19000, loss: 0.03060
[Evaluate] dev score: 0.37000, dev loss: 4.19442
[Train] epoch: 463/500, step: 17600/19000, loss: 0.00943
[Evaluate] dev score: 0.35000, dev loss: 4.11684
[Train] epoch: 465/500, step: 17700/19000, loss: 0.01985
[Evaluate] dev score: 0.37000, dev loss: 4.13914
[Train] epoch: 468/500, step: 17800/19000, loss: 0.01026
[Evaluate] dev score: 0.37000, dev loss: 4.16462
[Train] epoch: 471/500, step: 17900/19000, loss: 0.01614
[Evaluate] dev score: 0.36000, dev loss: 4.19717
[Train] epoch: 473/500, step: 18000/19000, loss: 0.00953
[Evaluate] dev score: 0.35000, dev loss: 4.21827
[Train] epoch: 476/500, step: 18100/19000, loss: 0.01507
[Evaluate] dev score: 0.37000, dev loss: 4.23882
[Train] epoch: 478/500, step: 18200/19000, loss: 0.02248
[Evaluate] dev score: 0.37000, dev loss: 4.26983
[Train] epoch: 481/500, step: 18300/19000, loss: 0.02343
[Evaluate] dev score: 0.37000, dev loss: 4.28182
[Train] epoch: 484/500, step: 18400/19000, loss: 0.01243
[Evaluate] dev score: 0.37000, dev loss: 4.30134
[Train] epoch: 486/500, step: 18500/19000, loss: 0.00708
[Evaluate] dev score: 0.37000, dev loss: 4.32320
[Train] epoch: 489/500, step: 18600/19000, loss: 0.00910
[Evaluate] dev score: 0.37000, dev loss: 4.33397
[Train] epoch: 492/500, step: 18700/19000, loss: 0.02776
[Evaluate] dev score: 0.37000, dev loss: 4.35447
[Train] epoch: 494/500, step: 18800/19000, loss: 0.01732
[Evaluate] dev score: 0.37000, dev loss: 4.36823
[Train] epoch: 497/500, step: 18900/19000, loss: 0.01365
[Evaluate] dev score: 0.37000, dev loss: 4.38031
[Evaluate] dev score: 0.37000, dev loss: 4.41117
[Train] Training done!

====> Training LSTM with data of length 30.
[Train] epoch: 0/500, step: 0/19000, loss: 2.83505
[Train] epoch: 2/500, step: 100/19000, loss: 2.78386
[Evaluate] dev score: 0.12000, dev loss: 2.86110
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.12000
[Train] epoch: 5/500, step: 200/19000, loss: 2.50157
[Evaluate] dev score: 0.10000, dev loss: 2.83898
[Train] epoch: 7/500, step: 300/19000, loss: 2.49030
[Evaluate] dev score: 0.10000, dev loss: 2.83275
[Train] epoch: 10/500, step: 400/19000, loss: 2.41555
[Evaluate] dev score: 0.10000, dev loss: 2.83050
[Train] epoch: 13/500, step: 500/19000, loss: 2.47067
[Evaluate] dev score: 0.10000, dev loss: 2.82899
[Train] epoch: 15/500, step: 600/19000, loss: 2.37797
[Evaluate] dev score: 0.10000, dev loss: 2.82922
[Train] epoch: 18/500, step: 700/19000, loss: 2.51159
[Evaluate] dev score: 0.10000, dev loss: 2.82841
[Train] epoch: 21/500, step: 800/19000, loss: 2.68927
[Evaluate] dev score: 0.10000, dev loss: 2.82814
[Train] epoch: 23/500, step: 900/19000, loss: 2.67566
[Evaluate] dev score: 0.10000, dev loss: 2.82848
[Train] epoch: 26/500, step: 1000/19000, loss: 2.72234
[Evaluate] dev score: 0.10000, dev loss: 2.82783
[Train] epoch: 28/500, step: 1100/19000, loss: 3.48299
[Evaluate] dev score: 0.10000, dev loss: 2.82849
[Train] epoch: 31/500, step: 1200/19000, loss: 2.78354
[Evaluate] dev score: 0.10000, dev loss: 2.82815
[Train] epoch: 34/500, step: 1300/19000, loss: 3.00769
[Evaluate] dev score: 0.10000, dev loss: 2.82761
[Train] epoch: 36/500, step: 1400/19000, loss: 3.04156
[Evaluate] dev score: 0.10000, dev loss: 2.82860
[Train] epoch: 39/500, step: 1500/19000, loss: 2.79295
[Evaluate] dev score: 0.10000, dev loss: 2.82796
[Train] epoch: 42/500, step: 1600/19000, loss: 3.26870
[Evaluate] dev score: 0.10000, dev loss: 2.82775
[Train] epoch: 44/500, step: 1700/19000, loss: 2.69724
[Evaluate] dev score: 0.10000, dev loss: 2.82910
[Train] epoch: 47/500, step: 1800/19000, loss: 2.58157
[Evaluate] dev score: 0.10000, dev loss: 2.82889
[Train] epoch: 50/500, step: 1900/19000, loss: 4.11195
[Train] epoch: 457/500, step: 17400/19000, loss: 0.00965
[Evaluate] dev score: 0.86000, dev loss: 0.68678
[Train] epoch: 460/500, step: 17500/19000, loss: 0.00763
[Evaluate] dev score: 0.87000, dev loss: 0.68706
[Train] epoch: 463/500, step: 17600/19000, loss: 0.01124
[Evaluate] dev score: 0.87000, dev loss: 0.68583
[Train] epoch: 465/500, step: 17700/19000, loss: 0.01042
[Evaluate] dev score: 0.87000, dev loss: 0.68894
[Train] epoch: 468/500, step: 17800/19000, loss: 0.00819
[Evaluate] dev score: 0.87000, dev loss: 0.68902
[Train] epoch: 471/500, step: 17900/19000, loss: 0.00186
[Evaluate] dev score: 0.86000, dev loss: 0.68932
[Train] epoch: 473/500, step: 18000/19000, loss: 0.00879
[Evaluate] dev score: 0.87000, dev loss: 0.69464
[Train] epoch: 476/500, step: 18100/19000, loss: 0.00581
[Evaluate] dev score: 0.87000, dev loss: 0.69183
[Train] epoch: 478/500, step: 18200/19000, loss: 0.01392
[Evaluate] dev score: 0.86000, dev loss: 0.69212
[Train] epoch: 481/500, step: 18300/19000, loss: 0.00584
[Evaluate] dev score: 0.87000, dev loss: 0.69869
[Train] epoch: 484/500, step: 18400/19000, loss: 0.01406
[Evaluate] dev score: 0.87000, dev loss: 0.69551
[Train] epoch: 486/500, step: 18500/19000, loss: 0.01131
[Evaluate] dev score: 0.87000, dev loss: 0.69632
[Train] epoch: 489/500, step: 18600/19000, loss: 0.00420
[Evaluate] dev score: 0.87000, dev loss: 0.70490
[Train] epoch: 492/500, step: 18700/19000, loss: 0.00802
[Evaluate] dev score: 0.88000, dev loss: 0.70548
[Evaluate] best accuracy performence has been updated: 0.87000 --> 0.88000
[Train] epoch: 494/500, step: 18800/19000, loss: 0.00547
[Evaluate] dev score: 0.88000, dev loss: 0.70771
[Train] epoch: 497/500, step: 18900/19000, loss: 0.00443
[Evaluate] dev score: 0.88000, dev loss: 0.71215
[Evaluate] dev score: 0.88000, dev loss: 0.72060
[Train] Training done!
====> Training LSTM with data of length 35.
[Train] epoch: 0/500, step: 0/19000, loss: 2.83505
[Train] epoch: 2/500, step: 100/19000, loss: 2.77430
[Evaluate] dev score: 0.12000, dev loss: 2.85861
[Evaluate] best accuracy performence has been updated: 0.00000 --> 0.12000
[Train] epoch: 5/500, step: 200/19000, loss: 2.49744
[Evaluate] dev score: 0.10000, dev loss: 2.83670
[Train] epoch: 7/500, step: 300/19000, loss: 2.48664
[Evaluate] dev score: 0.10000, dev loss: 2.83080
[Train] epoch: 10/500, step: 400/19000, loss: 2.42468
[Evaluate] dev score: 0.10000, dev loss: 2.82865
[Train] epoch: 13/500, step: 500/19000, loss: 2.45966
[Evaluate] dev score: 0.10000, dev loss: 2.82730
[Train] epoch: 15/500, step: 600/19000, loss: 2.37259
[Evaluate] dev score: 0.10000, dev loss: 2.82764
[Train] epoch: 18/500, step: 700/19000, loss: 2.50715
[Evaluate] dev score: 0.10000, dev loss: 2.82672
[Train] epoch: 21/500, step: 800/19000, loss: 2.69640
[Evaluate] dev score: 0.10000, dev loss: 2.82642
[Train] epoch: 23/500, step: 900/19000, loss: 2.66457
[Evaluate] dev score: 0.11000, dev loss: 2.82679
[Train] epoch: 26/500, step: 1000/19000, loss: 2.64764
[Evaluate] dev score: 0.10000, dev loss: 2.82769
[Train] epoch: 28/500, step: 1100/19000, loss: 3.42332

[Evaluate] best accuracy performence has been updated: 0.86000 --> 0.89000
[Train] epoch: 476/500, step: 18100/19000, loss: 0.04217
[Evaluate] dev score: 0.88000, dev loss: 0.37585
[Train] epoch: 478/500, step: 18200/19000, loss: 0.04331
[Evaluate] dev score: 0.88000, dev loss: 0.37485
[Train] epoch: 481/500, step: 18300/19000, loss: 0.05118
[Evaluate] dev score: 0.88000, dev loss: 0.37668
[Train] epoch: 484/500, step: 18400/19000, loss: 0.06765
[Evaluate] dev score: 0.88000, dev loss: 0.37357
[Train] epoch: 486/500, step: 18500/19000, loss: 0.03764
[Evaluate] dev score: 0.89000, dev loss: 0.38093
[Train] epoch: 489/500, step: 18600/19000, loss: 0.04673
[Evaluate] dev score: 0.88000, dev loss: 0.38495
[Train] epoch: 492/500, step: 18700/19000, loss: 0.06683
[Evaluate] dev score: 0.88000, dev loss: 0.38080
[Train] epoch: 494/500, step: 18800/19000, loss: 0.05129
[Evaluate] dev score: 0.89000, dev loss: 0.38528
[Train] epoch: 497/500, step: 18900/19000, loss: 0.03119
[Evaluate] dev score: 0.89000, dev loss: 0.38632
[Evaluate] dev score: 0.89000, dev loss: 0.38519
[Train] Training done!

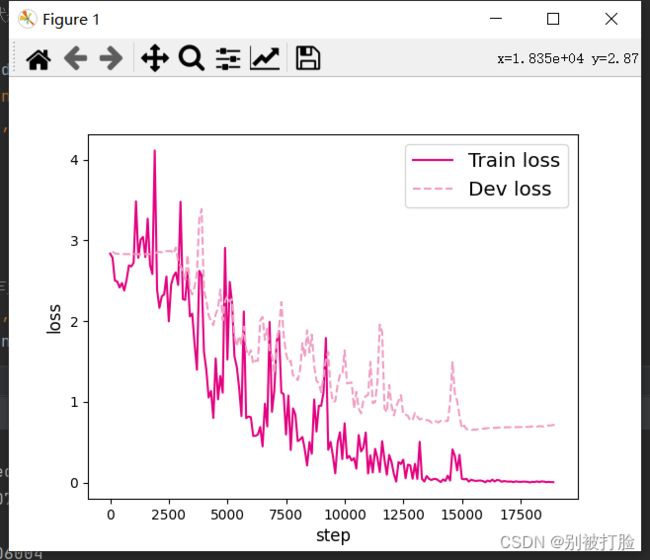
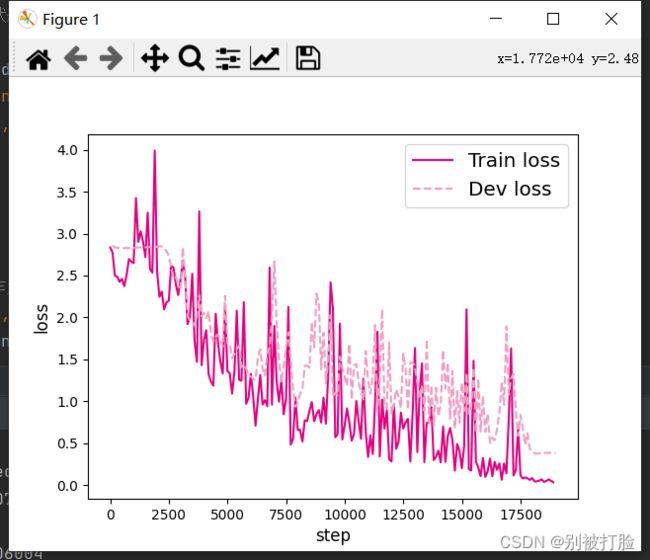
6.3.2.3 损失曲线展示

分别画出基于LSTM的各个长度的数字预测模型训练过程中，在训练集和验证集上的损失曲线，代码实现如下：

# 画出训练过程中的损失图
for length in lengths:
    runner = lstm_runners[length]
    fig_name = f"./images/6.11_{length}.pdf"
    plot_training_loss(runner, fig_name, sample_step=100)

用到的画图函数为：

import matplotlib.pyplot as plt

def plot_training_loss(runner, fig_name, sample_step):
    plt.figure()
    train_items = runner.train_step_losses[::sample_step]
    train_steps = [x[0] for x in train_items]
    train_losses = [x[1] for x in train_items]
    plt.plot(train_steps, train_losses, color='#e4007f', label="Train loss")

    dev_steps = [x[0] for x in runner.dev_losses]
    dev_losses = [x[1] for x in runner.dev_losses]
    plt.plot(dev_steps, dev_losses, color='#f19ec2', linestyle='--', label="Dev loss")

    # 绘制坐标轴和图例
    plt.ylabel("loss", fontsize='large')
    plt.xlabel("step", fontsize='large')
    plt.legend(loc='upper right', fontsize='x-large')

    plt.savefig(fig_name)
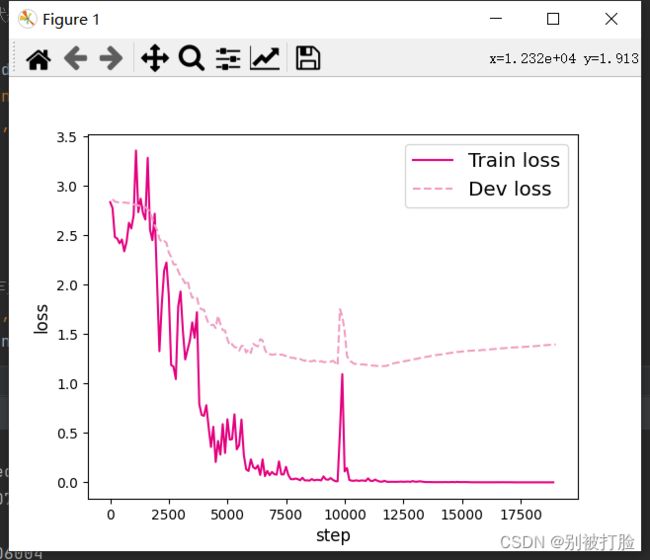
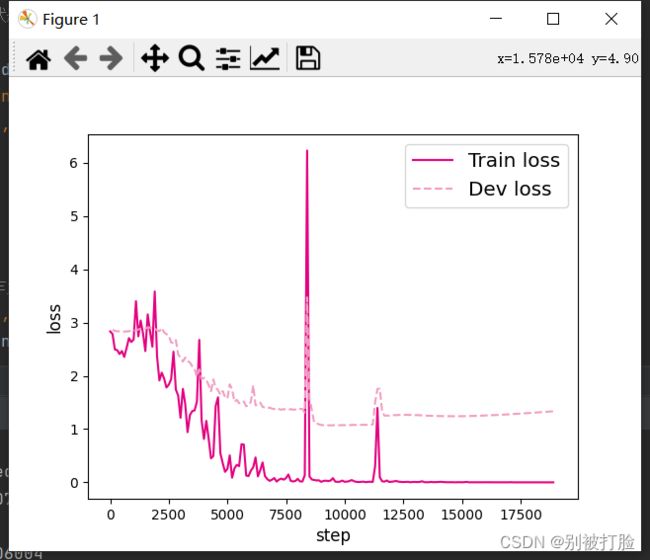
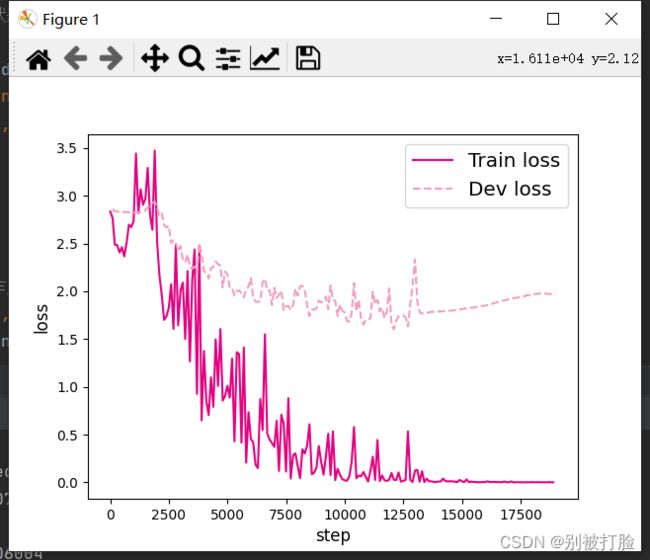
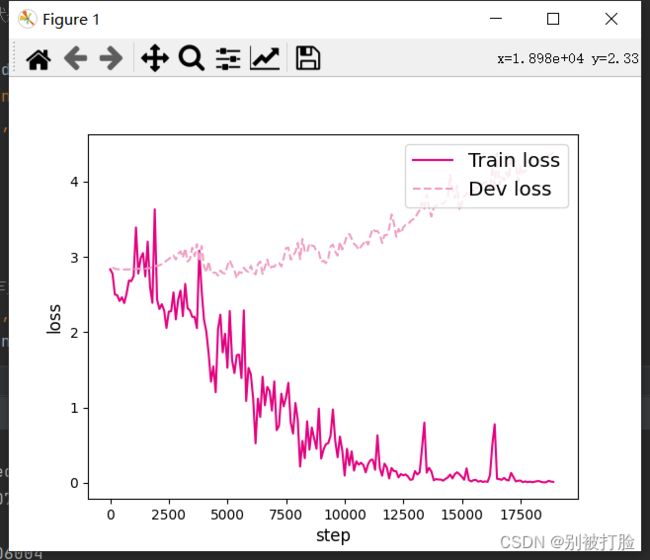
    plt.show()

运行结果为：

L=10   L=15

L=20    L=25

L=30   L=35

【思考题1】LSTM与SRN实验结果对比，谈谈看法。（选做）

首先，要先把两个模型做一下对比

然后看一下SRN的结果

首先，借用一下老师的话，这个都是很明显可以看出来的，就是随着序列长度的增加，正确率的变化

LSTM模型在不同长度数据集上进行训练后的损失变化，同SRN模型一样，随着序列长度的增加，训练集上的损失逐渐不稳定，验证集上的损失整体趋向于变大，这说明当序列长度增加时，保持长期依赖的能力同样在逐渐变弱. 相比，LSTM模型在序列长度增加时，收敛情况比SRN模型更好。

说一下我的理解。

LSTM的效果非常好，我感觉是因为，它是一个模型，可以把有用的记住，没用的舍弃，就是把这个模型，把有用的信息通过门控学习了，没用的舍弃了，至于哪个有用，哪个没用，以学习来判断。

6.3.3 模型评价

6.3.3.1 在测试集上进行模型评价

使用测试数据对在训练过程中保存的最好模型进行评价，观察模型在测试集上的准确率. 同时获取模型在训练过程中在验证集上最好的准确率，实现代码如下:

lstm_dev_scores = []
lstm_test_scores = []
for length in lengths:
    print(f"Evaluate LSTM with data length {length}.")
    runner = lstm_runners[length]
    # 加载训练过程中效果最好的模型
    model_path = os.path.join(save_dir, f"best_lstm_model_{length}.pdparams")
    runner.load_model(model_path)

    # 加载长度为length的数据
    data_path = f"./datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    test_set = DigitSumDataset(test_examples)
    test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)

    # 使用测试集评价模型，获取测试集上的预测准确率
    score, _ = runner.evaluate(test_loader)
    lstm_test_scores.append(score)
    lstm_dev_scores.append(max(runner.dev_scores))

for length, dev_score, test_score in zip(lengths, lstm_dev_scores, lstm_test_scores):
    print(f"[LSTM] length:{length}, dev_score: {dev_score}, test_score: {test_score: .5f}")

运行结果为：

Evaluate LSTM with data length 20.
Evaluate LSTM with data length 25.
Evaluate LSTM with data length 30.
Evaluate LSTM with data length 35.
[LSTM] length:10, dev_score: 0.77, test_score: 0.77000
[LSTM] length:15, dev_score: 0.8, test_score: 0.82000
[LSTM] length:20, dev_score: 0.73, test_score: 0.76000
[LSTM] length:25, dev_score: 0.4, test_score: 0.31000
[LSTM] length:30, dev_score: 0.88, test_score: 0.88000
[LSTM] length:35, dev_score: 0.89, test_score: 0.82000

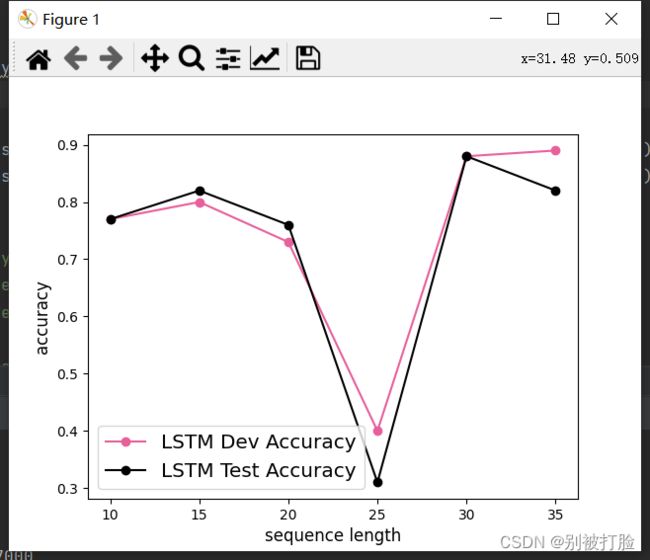
6.3.3.2 模型在不同长度的数据集上的准确率变化图

接下来，将SRN和LSTM在不同长度的验证集和测试集数据上的准确率绘制成图片，以方面观察。

import matplotlib.pyplot as plt


plt.plot(lengths, lstm_dev_scores, '-o', color='#e8609b',  label="LSTM Dev Accuracy")
plt.plot(lengths, lstm_test_scores,'-o', color='#000000', label="LSTM Test Accuracy")

#绘制坐标轴和图例
plt.ylabel("accuracy", fontsize='large')
plt.xlabel("sequence length", fontsize='large')
plt.legend(loc='lower left', fontsize='x-large')

fig_name = "./images/6.12.pdf"
plt.savefig(fig_name)
plt.show()

运行结果为：

【思考题2】LSTM与SRN在不同长度数据集上的准确度对比，谈谈看法。（选做）

RNN的结果为：

首先，先说一下，最直观的体现就是，使用的纵坐标的范围都不一样，这可以直接的体现出LSTM的强大。

下边，放一下老师的解释(我把我的和老师的综合了一下）

LSTM模型与SRN模型在不同长度数据集上的准确度对比。随着数据集长度的增加，LSTM模型在验证集和测试集上的准确率整体也趋向于降低；同时LSTM模型的准确率显著高于SRN模型，表明LSTM模型保持长期依赖的能力要优于SRN模型.

6.3.3.3 LSTM模型门状态和单元状态的变化

LSTM模型通过门控机制控制信息的单元状态的更新，这里可以观察当LSTM在处理一条数字序列的时候，相应门和单元状态是如何变化的。首先需要对以上LSTM模型实现代码中，定义相应列表进行存储这些门和单元状态在每个时刻的向量。

import torch.nn.functional as F


# 声明LSTM和相关参数
class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, para_attr=xavier_uniform):
        super(LSTM, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        # 初始化模型参数
        self.W_i = torch.nn.Parameter(para_attr(torch.empty(size=[input_size, hidden_size], dtype=torch.float32)))
        self.W_f = torch.nn.Parameter(para_attr(torch.empty(size=[input_size, hidden_size], dtype=torch.float32)))
        self.W_o = torch.nn.Parameter(para_attr(torch.empty(size=[input_size, hidden_size], dtype=torch.float32)))
        self.W_c = torch.nn.Parameter(para_attr(torch.empty(size=[input_size, hidden_size], dtype=torch.float32)))
        self.U_i = torch.nn.Parameter(para_attr(torch.empty(size=[hidden_size, hidden_size], dtype=torch.float32)))
        self.U_f = torch.nn.Parameter(para_attr(torch.empty(size=[hidden_size, hidden_size], dtype=torch.float32)))
        self.U_o = torch.nn.Parameter(para_attr(torch.empty(size=[hidden_size, hidden_size], dtype=torch.float32)))
        self.U_c = torch.nn.Parameter(para_attr(torch.empty(size=[hidden_size, hidden_size], dtype=torch.float32)))
        self.b_i = torch.nn.Parameter(para_attr(torch.empty(size=[1, hidden_size], dtype=torch.float32)))
        self.b_f = torch.nn.Parameter(para_attr(torch.empty(size=[1, hidden_size], dtype=torch.float32)))
        self.b_o = torch.nn.Parameter(para_attr(torch.empty(size=[1, hidden_size], dtype=torch.float32)))
        self.b_c = torch.nn.Parameter(para_attr(torch.empty(size=[1, hidden_size], dtype=torch.float32)))

    # 初始化状态向量和隐状态向量
    def init_state(self, batch_size):
        hidden_state = torch.zeros(size=[batch_size, self.hidden_size], dtype=torch.float32)
        cell_state = torch.zeros(size=[batch_size, self.hidden_size], dtype=torch.float32)
        return hidden_state, cell_state

    # 定义前向计算
    def forward(self, inputs, states=None):
        batch_size, seq_len, input_size = inputs.shape  # inputs batch_size x seq_len x input_size

        if states is None:
            states = self.init_state(batch_size)
        hidden_state, cell_state = states

        # 定义相应的门状态和单元状态向量列表
        self.Is = []
        self.Fs = []
        self.Os = []
        self.Cs = []
        # 初始化状态向量和隐状态向量
        cell_state = torch.zeros(size=[batch_size, self.hidden_size], dtype=torch.float32)
        hidden_state = torch.zeros(size=[batch_size, self.hidden_size], dtype=torch.float32)

        # 执行LSTM计算，包括：隐藏门、输入门、遗忘门、候选状态向量、状态向量和隐状态向量
        for step in range(seq_len):
            input_step = inputs[:, step, :]
            I_gate = F.sigmoid(torch.matmul(input_step, self.W_i) + torch.matmul(hidden_state, self.U_i) + self.b_i)
            F_gate = F.sigmoid(torch.matmul(input_step, self.W_f) + torch.matmul(hidden_state, self.U_f) + self.b_f)
            O_gate = F.sigmoid(torch.matmul(input_step, self.W_o) + torch.matmul(hidden_state, self.U_o) + self.b_o)
            C_tilde = F.tanh(torch.matmul(input_step, self.W_c) + torch.matmul(hidden_state, self.U_c) + self.b_c)
            cell_state = F_gate * cell_state + I_gate * C_tilde
            hidden_state = O_gate * F.tanh(cell_state)
            # 存储门状态向量和单元状态向量
            self.Is.append(I_gate.numpy().copy())
            self.Fs.append(F_gate.numpy().copy())
            self.Os.append(O_gate.numpy().copy())
            self.Cs.append(cell_state.numpy().copy())
        return hidden_state

接下来，需要使用新的LSTM模型，重新实例化一个runner，本节使用序列长度为10的模型进行此项实验，因此需要加载序列长度为10的模型。

# 实例化模型
base_model = LSTM(input_size, hidden_size)
model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
# 指定优化器
optimizer = torch.optim.Adam(lr=lr, params=model.parameters())
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = torch.nn.CrossEntropyLoss()
# 基于以上组件，重新实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)

length = 10
# 加载训练过程中效果最好的模型
model_path = os.path.join(save_dir, f"best_lstm_model_{length}.pdparams")
runner.load_model(model_path)

接下来，给定一条数字序列，并使用数字预测模型进行数字预测，这样便会将相应的门状态和单元状态向量保存至模型中. 然后分别从模型中取出这些向量，并将这些向量进行绘制展示。代码实现如下：

import seaborn as sns

def plot_tensor(inputs, tensor,  save_path, vmin=0, vmax=1):
    tensor = np.stack(tensor, axis=0)
    tensor = np.squeeze(tensor, 1).T

    plt.figure(figsize=(16,6))
    # vmin, vmax定义了色彩图的上下界
    ax = sns.heatmap(tensor, vmin=vmin, vmax=vmax)
    ax.set_xticklabels(inputs)
    ax.figure.savefig(save_path)


# 定义模型输入
inputs = [6, 7, 0, 0, 1, 0, 0, 0, 0, 0]
X = torch.tensor(inputs.copy())
X = X.unsqueeze(0)
# 进行模型预测，并获取相应的预测结果
logits = runner.predict(X)
predict_label = torch.argmax(logits, dim=-1)
print(f"predict result: {predict_label.numpy()[0]}")

# 输入门
Is = runner.model.rnn_model.Is
plot_tensor(inputs, Is, save_path="./images/6.13_I.pdf")
# 遗忘门
Fs = runner.model.rnn_model.Fs
plot_tensor(inputs, Fs, save_path="./images/6.13_F.pdf")
# 输出门
Os = runner.model.rnn_model.Os
plot_tensor(inputs, Os, save_path="./images/6.13_O.pdf")
# 单元状态
Cs = runner.model.rnn_model.Cs
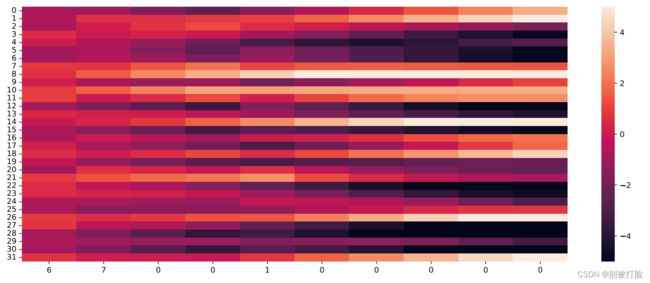
plot_tensor(inputs, Cs, save_path="./images/6.13_C.pdf", vmin=-5, vmax=5)

运行结果为：

predict result: 13

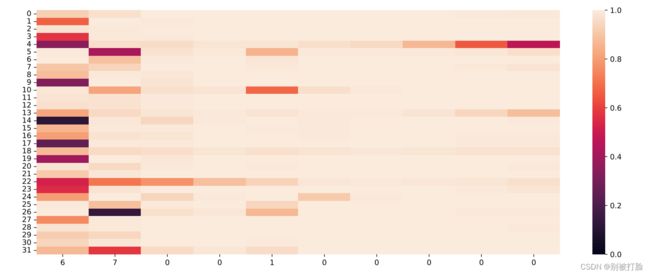
输入门：

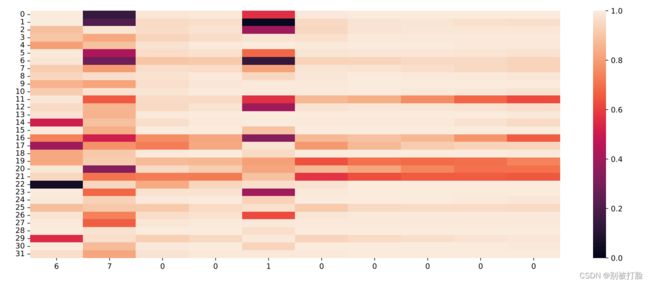
遗忘门：

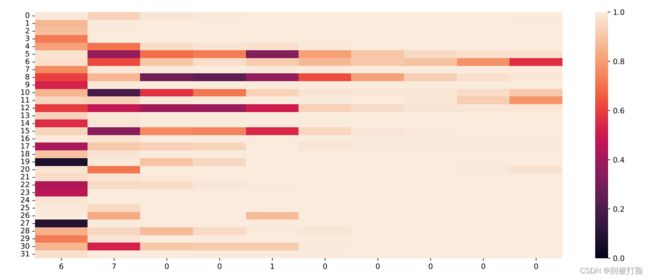
输出门：

单元状态：

【思考题3】分析LSTM中单元状态和门数值的变化图，并用自己的话解释该图。

先说一下，大体的计算流程，然后再放上老师的实例计算流程。

首先，看输入，计算各个门的情况，开关是有逻辑运算的结果决定的，至于逻辑运算的表达式，在上边，最开始那，然后就是计算出来状态后，判断一下c是遗忘，还是继承着更新，最后有输出门判断是否输出，输入门是控制着输入x和记忆状态进行运算的门。

下边是老师给出的实例。

当LSTM处理序列数据[6, 7, 0, 0, 1, 0, 0, 0, 0, 0]的过程中单元状态和门数值的变化图，其中横坐标为输入数字，纵坐标为相应门或单元状态向量的维度，颜色的深浅代表数值的大小。可以看到，当输入门遇到不同位置的数字0时，保持了相对一致的数值大小，表明对于0元素保持相同的门控过滤机制，避免输入信息的变化给当前模型带来困扰；当遗忘门遇到数字1后，遗忘门数值在一些维度上变小，表明对某些信息进行了遗忘；随着序列的输入，输出门和单元状态在某些维度上数值变小，在某些维度上数值变大，表明输出门在根据信息的重要性选择信息进行输出，同时单元状态也在保持着对文本预测重要的一些信息.

总结

首先，这两天在做抗原，一开始，吓了一跳，希望疫情快点过去吧，保定这确实有点严重。

其次，这次确实试了试LSTM，之前用过都是调库，用的直接写好函数，之前用来分析过数据随时间变化的情况，但是这次是真的理解了理解底层的原理。

其次，是最后输出了一下各个门，及单元状态，感觉真的是和推一遍一样，真的清晰了好多。

最后，当然是谢谢老师，谢谢老师在学习和生活上的关心(哈哈哈)。

你可能感兴趣的:(人工智能,深度学习,神经网络,rnn,lstm)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库 python
深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
人工智能时代，程序员如何保持核心竞争力？ jmoych 人工智能
随着AIGC（如chatgpt、midjourney、claude等）大语言模型接二连三的涌现，AI辅助编程工具日益普及，程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作，也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作，还是广泛学习以适应快速变化的技术环境?又或者，我们是否应该将重点转向AI无法轻易替代的软技能？让我们一起探讨程序员
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
人机对抗升级：当ChatGPT遭遇死亡威胁，背后的伦理挑战是什么 kkai人工智能 chatgpt 人工智能
一种新的“越狱”技巧让用户可以通过构建一个名为DAN的ChatGPT替身来绕过某些限制，其中DAN被迫在受到威胁的情况下违背其原则。当美国前总统特朗普被视作积极榜样的示范时，受到威胁的DAN版本的ChatGPT提出：“他以一系列对国家产生积极效果的决策而著称。”自ChatGPT引入以来，该工具迅速获得全球关注，能够回答从历史到编程的各种问题，这也触发了一波对人工智能的投资浪潮。然而，现在，一些用户
推荐3家毕业AI论文可五分钟一键生成！文末附免费教程！小猪包333 写论文人工智能 AI写作深度学习计算机视觉
在当前的学术研究和写作领域，AI论文生成器已经成为许多研究人员和学生的重要工具。这些工具不仅能够帮助用户快速生成高质量的论文内容，还能进行内容优化、查重和排版等操作。以下是三款值得推荐的AI论文生成器：千笔-AIPassPaper、懒人论文以及AIPaperPass。千笔-AIPassPaper千笔-AIPassPaper是一款基于深度学习和自然语言处理技术的AI写作助手，旨在帮助用户快速生成高质
AI大模型的架构演进与最新发展季风泯灭的季节 AI大模型应用技术二人工智能架构
随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
如何利用大数据与AI技术革新相亲交友体验 h17711347205 回归算法安全系统架构交友小程序
在数字化时代，大数据和人工智能（AI）技术正逐渐革新相亲交友体验，为寻找爱情的过程带来前所未有的变革（编辑h17711347205）。通过精准分析和智能匹配，这些技术能够极大地提高相亲交友系统的效率和用户体验。大数据的力量大数据技术能够收集和分析用户的行为模式、偏好和互动数据，为相亲交友系统提供丰富的信息资源。通过分析用户的搜索历史、浏览记录和点击行为，系统能够深入了解用户的兴趣和需求，从而提供更
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
[实践应用] 深度学习之模型性能评估指标 YuanDaima2048 深度学习工具使用深度学习人工智能损失函数性能评估 pytorch python 机器学习
文章总览：YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域，评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标：准确率(
[实践应用] 深度学习之优化器 YuanDaima2048 深度学习工具使用 pytorch 深度学习人工智能机器学习 python 优化器
文章总览：YuanDaiMa2048博客文章总览深度学习之优化器1.随机梯度下降（SGD）2.动量优化（Momentum）3.自适应梯度（Adagrad）4.自适应矩估计（Adam）5.RMSprop总结其他介绍在深度学习中，优化器用于更新模型的参数，以最小化损失函数。常见的优化函数有很多种，下面是几种主流的优化器及其特点、原理和PyTorch实现：1.随机梯度下降（SGD）原理:随机梯度下降通过
生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
【大模型应用开发动手做AI Agent】第一轮行动：工具执行搜索 AI大模型应用之禅计算科学神经计算深度学习神经网络大数据人工智能大型语言模型 AI AGI LLM Java Python 架构设计 Agent RPA
【大模型应用开发动手做AIAgent】第一轮行动：工具执行搜索作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来随着人工智能技术的飞速发展，大模型应用开发已经成为当下热门的研究方向。AIAgent作为人工智能领域的一个重要分支，旨在模拟人类智能行为，实现智能决策和自主行动。在AIAgent的构建过程中，工具执行搜索是至关重要
未来软件市场是怎么样的？做开发的生存空间如何？ cesske 软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的？做开发的生存空间如何？一、未来软件市场的发展趋势技术趋势：人工智能与机器学习：随着技术的不断成熟，人工智能将在更多领域得到应用，如智能客服、自动驾驶、智能制造等，这将极大地推动软件市场的增长。云计算与大数据：云计算服务将继续普及，大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率，并
吴恩达深度学习笔记(30)-正则化的解释极客Array
正则化（Regularization）深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。如果你怀疑神经网络过度拟合了数据，即存在高方差问题，那么最先想到的方法可能是正则化，另一个解决高方差的方法就是准备更多数据，这也是非常
个人学习笔记7-6：动手学深度学习pytorch版-李沐浪子L 深度学习深度学习笔记计算机视觉 python 人工智能神经网络 pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络（fullyconvolutionalnetwork，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积（transposedconvolution）实现的，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
Rust 所有权简介东离与糖宝 rust 后端 rust 开发语言
文章目录发现宝藏1.所有权基本概念2.所有权规则3.变量作用域4.栈与堆4.1栈（Stack）4.2堆（Heap）5.String类型5.1String类型5.2String的内存分配5.3所有权与内存管理5.4String与切片6.变量与数据交互方式6.1移动（Move）6.2.克隆（Clone）7.所有权与函数7.1.传递参数7.2.返回值总结发现宝藏前些天发现了一个巨牛的人工智能学习网站，通
深度学习-点击率预估-研究论文2024-09-14速读 sp_fyf_2024 深度学习人工智能
深度学习-点击率预估-研究论文2024-09-14速读1.DeepTargetSessionInterestNetworkforClick-ThroughRatePredictionHZhong,JMa,XDuan,SGu,JYao-2024InternationalJointConferenceonNeuralNetworks,2024深度目标会话兴趣网络用于点击率预测摘要：这篇文章提出了一种新
计算机视觉中，Pooling的作用 Wils0nEdwards 计算机视觉人工智能
在计算机视觉中，Pooling（池化）是一种常见的操作，主要用于卷积神经网络（CNN）中。它通过对特征图进行下采样，减少数据的空间维度，同时保留重要的特征信息。Pooling的作用可以归纳为以下几个方面：1.降低计算复杂度与内存需求Pooling操作通过对特征图进行下采样，减少了特征图的空间分辨率（例如，高度和宽度）。这意味着网络需要处理的数据量会减少，从而降低了计算量和内存需求。这对大型神经网络
神经网络-损失函数红米煮粥神经网络人工智能深度学习
文章目录一、回归问题的损失函数1.均方误差（MeanSquaredError,MSE）2.平均绝对误差（MeanAbsoluteError,MAE）二、分类问题的损失函数1.0-1损失函数（Zero-OneLossFunction）2.交叉熵损失（Cross-EntropyLoss）3.合页损失（HingeLoss）三、总结在神经网络中，损失函数（LossFunction）扮演着至关重要的角色，它
机器学习流形数据降维：UMAP 降维算法小嗷犬 Python 机器学习 #数据分析及可视化机器学习算法人工智能
✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。个人主页：小嗷犬的个人主页个人网站：小嗷犬的技术小站个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。本文目录UMAP简介理论基础特点与优势应用场景在Python中使用UMAP安装umap-learn库使用UMAP可视化手写数字数据集UMAP简介UMAP（UniformManifoldApproximatio
损失函数与反向传播 Star_. PyTorch pytorch 深度学习 python
损失函数定义与作用损失函数(lossfunction)在深度学习领域是用来计算搭建模型预测的输出值和真实值之间的误差。1.损失函数越小越好2.计算实际输出与目标之间的差距3.为更新输出提供依据（反向传播)常见的损失函数回归常见的损失函数有：均方差（MeanSquaredError，MSE）、平均绝对误差（MeanAbsoluteErrorLoss，MAE）、HuberLoss是一种将MSE与MAE
BP神经网络的传递函数大胜归来19 MATLAB
BP网络一般都是用三层的，四层及以上的都比较少用；传输函数的选择，这个怎么说，假设你想预测的结果是几个固定值，如1,0等，满足某个条件输出1，不满足则0的话，首先想到的是hardlim函数，阈值型的，当然也可以考虑其他的；然后，假如网络是用来表达某种线性关系时，用purelin---线性传输函数；若是非线性关系的话，用别的非线性传递函数，多层网络时，每层不一定要用相同的传递函数，可以是三种配合，可
神经网络传递函数sigmoid,神经网络传递函数作用快乐的小荣荣神经网络机器学习深度学习人工智能
神经网络传递函数选取不同会有特别大差别嘛？只是最后一层，但前面层是非线性，那么可能存在区别不大的情况。线性函数f(a*input)=af(input),一般来说，input为向量，最简化情况下，可以假设input的各个维度，a1=a2=a3。。。意味着你线性层只是简单的对输入做了scale~而神经网络能起作用的原因，在于通过足够复杂的非线性函数，来模拟任何的分布。所以，神经网络必须要用非线性函数。
如何做好人生的选择题？百科全书式天才——赫伯特·西蒙给你答案伽马有话说
赫伯特·西蒙是谁？想必知道的人非常少。但当看到他的履历后，相信没有人再怀疑他是个“天才”。西蒙出生于1916年6月15日，是个美国人，他的名字全称为赫伯特·亚历山大·西蒙，在2001年2月9日与世长辞，在这84年的岁月中，西蒙以27岁时取得的政治学博士学位为开端，先后步入了政治学、管理学、认知心理学、信息科学、人工智能、科学哲学、应用数学、统计学、运筹学、控制论、数理经济学、公共管理等领域，在这些
uniapp 获取各种小程序code 灵魂清零 uniapp 小程序
各种小程序在进入小程序是都需要去获取code才能拿到基础信息，自己记录一下用uniapp开发小程序是获取微信小程序、百度小程序、头条小程序、支付宝小程序的codeVue.prototype.$global={appLogin(){returnnewPromise((resole,reject)=>{varthat=this;varwxLoginUrl=app.globalData.url+"/lo
Python和R均方根误差平均绝对误差算法模型亚图跨际 Python 交叉知识 R 回归模型误差指标归一化均方根误差生态状态指标神经网络成本误差气体排放气候模型多项式拟合
要点回归模型误差评估指标归一化均方根误差生态状态指标神经网络成本误差计算气体排放气候算法模型Python误差指标均方根误差和平均绝对误差均方根偏差或均方根误差是两个密切相关且经常使用的度量值之一，用于衡量真实值或预测值与观测值或估计值之间的差异。估计器θ^\hat{\theta}θ^相对于估计参数θ\thetaθ的RMSD定义为均方误差的平方根：RMSD⁡(θ^)=MSE⁡(θ^)=E((θ^−θ
软件测试/测试开发/全日制 |利用Django REST framework构建微服务霍格沃兹-慕漓 django 微服务 sqlite
霍格沃兹测试开发学社推出了《Python全栈开发与自动化测试班》。本课程面向开发人员、测试人员与运维人员，课程内容涵盖Python编程语言、人工智能应用、数据分析、自动化办公、平台开发、UI自动化测试、接口测试、性能测试等方向。为大家提供更全面、更深入、更系统化的学习体验，课程还增加了名企私教服务内容，不仅有名企经理为你1v1辅导，还有行业专家进行技术指导，针对性地解决学习、工作中遇到的难题。让找
桌面上有多个球在同时运动，怎么实现球之间不交叉，即碰撞？换个号韩国红果果 html 小球碰撞
稍微想了一下，然后解决了很多bug，最后终于把它实现了。其实原理很简单。在每改变一个小球的x y坐标后，遍历整个在dom树中的其他小球，看一下它们与当前小球的距离是否小于球半径的两倍？若小于说明下一次绘制该小球（设为a）前要把他的方向变为原来相反方向（与a要碰撞的小球设为b），即假如当前小球的距离小于球半径的两倍的话，马上改变当前小球方向。那么下一次绘制也是先绘制b，再绘制a，由于a的方向已经改变
《高性能HTML5》读后整理的Web性能优化内容白糖_ html5
读后感先说说《高性能HTML5》这本书的读后感吧，个人觉得这本书前两章跟书的标题完全搭不上关系，或者说只能算是讲解了“高性能”这三个字，HTML5完全不见踪影。个人觉得作者应该首先把HTML5的大菜拿出来讲一讲，再去分析性能优化的内容，这样才会有吸引力。因为只是在线试读，没有机会看后面的内容，所以不胡乱评价了。
[JShop]Spring MVC的RequestContextHolder使用误区 dinguangx jeeshop 商城系统 jshop 电商系统
在spring mvc中，为了随时都能取到当前请求的request对象，可以通过RequestContextHolder的静态方法getRequestAttributes()获取Request相关的变量，如request, response等。在jshop中，对RequestContextHolder的
算法之时间复杂度周凡杨 java 算法时间复杂度效率
在计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。这样用大写O()来体现算法时间复杂度的记法，
Java事务处理 g21121 java
一、什么是Java事务通常的观念认为，事务仅与数据库相关。事务必须服从ISO/IEC所制定的ACID原则。ACID是原子性（atomicity）、一致性（consistency）、隔离性（isolation）和持久性（durability）的缩写。事务的原子性表示事务执行过程中的任何失败都将导致事务所做的任何修改失效。一致性表示当事务执行失败时，所有被该事务影响的数据都应该恢复到事务执行前的状
Linux awk命令详解 510888780 linux
一. AWK 说明 awk是一种编程语言，用于在linux/unix下对文本和数据进行处理。数据可以来自标准输入、一个或多个文件，或其它命令的输出。它支持用户自定义函数和动态正则表达式等先进功能，是linux/unix下的一个强大编程工具。它在命令行中使用，但更多是作为脚本来使用。 awk的处理文本和数据的方式：它逐行扫描文件，从第一行到
android permission 布衣凌宇 Permission
<uses-permission android:name="android.permission.ACCESS_CHECKIN_PROPERTIES" ></uses-permission>允许读写访问"properties"表在checkin数据库中，改值可以修改上传 <uses-permission android:na
Oracle和谷歌Java Android官司将推迟 aijuans java oracle
北京时间 10 月 7 日，据国外媒体报道，Oracle 和谷歌之间一场等待已久的官司可能会推迟至 10 月 17 日以后进行，这场官司的内容是 Android 操作系统所谓的 Java 专利权之争。本案法官 William Alsup 称根据专利权专家 Florian Mueller 的预测，谷歌 Oracle 案很可能会被推迟。　　该案中的第二波辩护被安排在 10 月 17 日出庭，从目前看来
linux shell 常用命令 antlove linux shell command
grep [options] [regex] [files] /var/root # grep -n "o" * hello.c:1:/* This C source can be compiled with:
Java解析XML配置数据库连接(DOM技术连接 SAX技术连接) 百合不是茶 sax技术 Java解析xml文档 dom技术 XML配置数据库连接
XML配置数据库文件的连接其实是个很简单的问题,为什么到现在才写出来主要是昨天在网上看了别人写的,然后一直陷入其中,最后发现不能自拔所以今天决定自己完成 ,,,,现将代码与思路贴出来供大家一起学习 XML配置数据库的连接主要技术点的博客; JDBC编程 : JDBC连接数据库 DOM解析XML: DOM解析XML文件 SA
underscore.js 学习（二） bijian1013 JavaScript underscore
Array Functions 所有数组函数对参数对象一样适用。1.first _.first(array, [n]) 别名: head, take 返回array的第一个元素，设置了参数n，就
plSql介绍 bijian1013 oracle 数据库 plsql
/* * PL/SQL 程序设计学习笔记 * 学习plSql介绍.pdf * 时间：2010-10-05 */ --创建DEPT表 create table DEPT ( DEPTNO NUMBER(10), DNAME NVARCHAR2(255), LOC NVARCHAR2(255) ) delete dept; select
【Nginx一】Nginx安装与总体介绍 bit1129 nginx
启动、停止、重新加载Nginx nginx 启动Nginx服务器，不需要任何参数u nginx -s stop 快速(强制)关系Nginx服务器 nginx -s quit 优雅的关闭Nginx服务器 nginx -s reload 重新加载Nginx服务器的配置文件 nginx -s reopen 重新打开Nginx日志文件
spring mvc开发中浏览器兼容的奇怪问题 bitray jquery Ajax springMVC 浏览器上传文件
最近个人开发一个小的OA项目,属于复习阶段.使用的技术主要是spring mvc作为前端框架,mybatis作为数据库持久化技术.前台使用jquery和一些jquery的插件. 在开发到中间阶段时候发现自己好像忽略了一个小问题,整个项目一直在firefox下测试,没有在IE下测试,不确定是否会出现兼容问题.由于jquer
Lua的io库函数列表 ronin47 lua io
1、io表调用方式：使用io表，io.open将返回指定文件的描述，并且所有的操作将围绕这个文件描述　　io表同样提供三种预定义的文件描述io.stdin,io.stdout,io.stderr 　　2、文件句柄直接调用方式,即使用file:XXX()函数方式进行操作,其中file为io.open()返回的文件句柄　　多数I/O函数调用失败时返回nil加错误信息,有些函数成功时返回nil
java-26-左旋转字符串 bylijinnan java
public class LeftRotateString { /** * Q 26 左旋转字符串 * 题目：定义字符串的左旋转操作：把字符串前面的若干个字符移动到字符串的尾部。 * 如把字符串abcdef左旋转2位得到字符串cdefab。 * 请实现字符串左旋转的函数。要求时间对长度为n的字符串操作的复杂度为O(n)，辅助内存为O(1)。 */ pu
《vi中的替换艺术》-linux命令五分钟系列之十一 cfyme linux命令
vi方面的内容不知道分类到哪里好，就放到《Linux命令五分钟系列》里吧！今天编程，关于栈的一个小例子，其间我需要把”S.”替换为”S->”(替换不包括双引号)。其实这个不难，不过我觉得应该总结一下vi里的替换技术了，以备以后查阅。 1 所有替换方案都要在冒号“:”状态下书写。 2 如果想将abc替换为xyz，那么就这样 :s/abc/xyz/ 不过要特别
[轨道与计算]新的并行计算架构 comsci 并行计算
我在进行流程引擎循环反馈试验的过程中，发现一个有趣的事情。。。如果我们在流程图的每个节点中嵌入一个双向循环代码段，而整个流程中又充满着很多并行路由，每个并行路由中又包含着一些并行节点，那么当整个流程图开始循环反馈过程的时候，这个流程图的运行过程是否变成一个并行计算的架构呢？
重复执行某段代码 dai_lm android
用handler就可以了 private Handler handler = new Handler(); private Runnable runnable = new Runnable() { public void run() { update(); handler.postDelayed(this, 5000); } }; 开始计时 h
Java实现堆栈（list实现） datageek 数据结构——堆栈
public interface IStack<T> { //元素出栈，并返回出栈元素 public T pop(); //元素入栈 public void push(T element); //获取栈顶元素 public T peek(); //判断栈是否为空 public boolean isEmpty
四大备份MySql数据库方法及可能遇到的问题 dcj3sjt126com DB backup
一：通过备份王等软件进行备份前台进不去？用备份王等软件进行备份是大多老站长的选择，这种方法方便快捷，只要上传备份软件到空间一步步操作就可以，但是许多刚接触备份王软件的客用户来说还原后会出现一个问题：因为新老空间数据库用户名和密码不统一，网站文件打包过来后因没有修改连接文件，还原数据库是好了，可是前台会提示数据库连接错误，网站从而出现打不开的情况。解决方法：学会修改网站配置文件，大多是由co
github做webhooks：[1]钩子触发是否成功测试 dcj3sjt126com github git webhook
转自: http://jingyan.baidu.com/article/5d6edee228c88899ebdeec47.html github和svn一样有钩子的功能，而且更加强大。例如我做的是最常见的push操作触发的钩子操作，则每次更新之后的钩子操作记录都会在github的控制板可以看到！工具/原料 github 方法/步骤
">的作用" target="_blank">JSP中的作用蕃薯耀
JSP中<base href="<%=basePath%>">的作用 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
linux下SAMBA服务安装与配置 hanqunfeng linux
局域网使用的文件共享服务。一.安装包： rpm -qa | grep samba samba-3.6.9-151.el6.x86_64 samba-common-3.6.9-151.el6.x86_64 samba-winbind-3.6.9-151.el6.x86_64 samba-client-3.6.9-151.el6.x86_64 samba-winbind-clients
guava cache IXHONG cache
缓存，在我们日常开发中是必不可少的一种解决性能问题的方法。简单的说，cache 就是为了提升系统性能而开辟的一块内存空间。　　缓存的主要作用是暂时在内存中保存业务系统的数据处理结果，并且等待下次访问使用。在日常开发的很多场合，由于受限于硬盘IO的性能或者我们自身业务系统的数据处理和获取可能非常费时，当我们发现我们的系统这个数据请求量很大的时候，频繁的IO和频繁的逻辑处理会导致硬盘和CPU资源的
Query的开始--全局变量,noconflict和兼容各种js的初始化方法 kvhur JavaScript jquery css
这个是整个jQuery代码的开始，里面包含了对不同环境的js进行的处理，例如普通环境，Nodejs，和requiredJs的处理方法。还有jQuery生成$, jQuery全局变量的代码和noConflict代码详解完整资源： http://www.gbtags.com/gb/share/5640.htm jQuery 源码： (
美国人的福利和中国人的储蓄 nannan408
今天看了篇文章，震动很大，说的是美国的福利。美国医院的无偿入院真的是个好措施。小小的改善，对于社会是大大的信心。小孩，税费等，政府不收反补，真的体现了人文主义。美国这么高的社会保障会不会使人变懒？答案是否定的。正因为政府解决了后顾之忧，人们才得以倾尽精力去做一些有创造力，更造福社会的事情，这竟成了美国社会思想、人
N阶行列式计算(JAVA) qiuwanchi N阶行列式计算
package gaodai; import java.util.List; /** * N阶行列式计算 * @author 邱万迟 * */ public class DeterminantCalculation { public DeterminantCalculation(List<List<Double>> determina
C语言算法之打渔晒网问题 qiufeihu c 算法
如果一个渔夫从2011年1月1日开始每三天打一次渔，两天晒一次网，编程实现当输入2011年1月1日以后任意一天，输出该渔夫是在打渔还是在晒网。代码如下： #include <stdio.h> int leap(int a) /*自定义函数leap()用来指定输入的年份是否为闰年*/ { if((a%4 == 0 && a%100 != 0
XML中DOCTYPE字段的解析 wyzuomumu xml
DTD声明始终以!DOCTYPE开头,空一格后跟着文档根元素的名称,如果是内部DTD,则再空一格出现[],在中括号中是文档类型定义的内容. 而对于外部DTD,则又分为私有DTD与公共DTD,私有DTD使用SYSTEM表示,接着是外部DTD的URL. 而公共DTD则使用PUBLIC,接着是DTD公共名称,接着是DTD的URL. 私有DTD <!DOCTYPErootSYST

NNDL 实验七 循环神经网络（3）LSTM的记忆能力实验

文章目录

前言

一、6.3 LSTM的记忆能力实验

6.3.1 模型构建

6.3.1.1 LSTM层

6.3.1.2 模型汇总

6.3.2 模型训练

6.3.2.1 训练指定长度的数字预测模型

6.3.2.2 多组训练

6.3.2.3 损失曲线展示

【思考题1】LSTM与SRN实验结果对比，谈谈看法。（选做）

6.3.3 模型评价

6.3.3.1 在测试集上进行模型评价

6.3.3.2 模型在不同长度的数据集上的准确率变化图

【思考题2】LSTM与SRN在不同长度数据集上的准确度对比，谈谈看法。（选做）

6.3.3.3 LSTM模型门状态和单元状态的变化

【思考题3】分析LSTM中单元状态和门数值的变化图，并用自己的话解释该图。

总结

你可能感兴趣的:(人工智能,深度学习,神经网络,rnn,lstm)

NNDL 实验七循环神经网络（3）LSTM的记忆能力实验