蒙特卡洛原理
蒙特卡洛方法的基本原理是,事件的概率可以用大量试验中发生的频率来估计,当样本容量足够大可以认为该事件的发生频率即为其概率.因此,可以先对影响其可靠度的随机变量进行大量的随机抽样,然后把这些抽样值一组一组地代入功能函数式,确定结构是否失效,最后从中求得结构的失效概率,蒙特卡洛法正是基于此思路进行分析的。蒙特卡洛方法在金融工程学、宏观经济学、计算、空气动力学计算)等领域应用广泛。
蒙特卡洛的基本做法是通过大量重复试验,通过统计频率,来估计概率,从而得到问题的求解。举个例子,如下图“蒙特卡洛法估计不规则图形面积”所示,一个矩形内有一个不规则图案,要求解不规则图形的面积。显然,矩形的面积可以简单计算为![]() ,点位于不规则形状内的概率为
,点位于不规则形状内的概率为![]() 。现在重复往矩形范围内随机的投射点,样本点有一定概率会落在不规则图形内,若复杂n次试验,落到不规则图形内的次数为k,频率为k/n,若样本数量较大则有:
。现在重复往矩形范围内随机的投射点,样本点有一定概率会落在不规则图形内,若复杂n次试验,落到不规则图形内的次数为k,频率为k/n,若样本数量较大则有:
![]()
1、硬币投掷实验
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%硬币投掷实验
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear
clc
p=0.5; %设置二项式分布binornd函数的概率
N=2000; %随机模拟的次数
sum=0;
for k=1:N
sum=sum+binornd(1,p); %投掷实验的正面统计(假设硬币朝上为正面binornd返回1)
P(k)=sum/k; %统计每次实验的硬币正面的概率
end
figure
hold on;box on;
plot(1:N,P);N=10000的模拟结果:
![]()
2、几何概率模拟实验
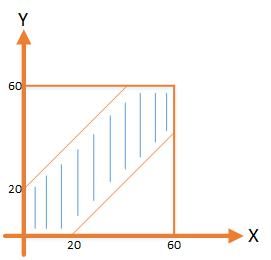
对于一些比较复杂的几何图像,不好采用微积分方法计算图像的面积或参数,可以采用蒙特卡洛投点模拟方法计算出图像的面积或参数。假设两个人在1:00—2:00这段时间约会,他们约定先到者等20分钟后未等到另一个人则可以离开,试问他们两个人见面的概率有多大。这道题我们可以假设条件然后画出条件对应的图像,在根据图像的面积比计算两个人见面的概率。
假设:![]() 和
和![]() 分别为两个人A、B到达的时间
分别为两个人A、B到达的时间
A、B会面的条件![]() ,如下图所示中间的条纹区域就是两个人会面的时间交集区域,中间条纹这块面积为
,如下图所示中间的条纹区域就是两个人会面的时间交集区域,中间条纹这块面积为![]()
所以中间条纹区域占整个面积的比例![]()
那么我们现在可以通过蒙特卡洛的方法来计算两个人会面的概率,我们通过生成随机数,然后统计落在条纹区域的随机数目再与总的随机数目对比,即得到两个人会面的概率,Matlab仿真程序如下:
%%%%%%%%%%%%%%%%%%%%%%%%%
%投点发模拟两人会面的概率
%%%%%%%%%%%%%%%%%%%%%%%%%
m=10000; %模拟的次数
success=0; %成功会面的次数
j = 1;
k = 1;
for i=1:m
x=unifrnd(0,60); %生成x随机数
y=unifrnd(0,60); %生成y随机数
if abs(x-y)<=20 %两个人成功会面
A1(j) = x; %A统计成功会面的坐标点
A2(j) = y;
success=success+1; %成功会面的次数
j=j+1;
end
if abs(x-y)>20 %未成功会面
B1(k) = x; %B统计未成功会面的坐标点
B2(k) = y;
k=k+1;
end
end
P=success/m %成会面的概率
plot(A1,A2,'. r',B1,B2,'. b','MarkerSize',5); %画图表示设置m=10000次的模拟,得出如下结论:
![]()
红色表示落在成功会面的区间,蓝色表示落在未成功会面的区间,红色点数与所有随机点数之比就得到了概率P,如下图所示:
3、蒲丰针实验-间接计算圆周率
18世纪蒲丰提出以下问题:设我们有一个等间距的平行线如图下图所示,随意抛一支长度比平行线之间距离小的针,求针和其中一条平行线相交的概率,并以此概率提出了一种计算圆周率的方法—随机投针法。
这一方法的步骤是:
1) 取一张白纸,在上面画上许多条间距为a的平行线。
2) 取一根长度为l(l≤a) 的针,随机地向画有平行直线的纸上掷n次,观察针与直线相交的次数,记为m。
3)计算针与直线相交的概率。
假设随机投掷的一根针与平行线的夹角为![]() ,夹角的范围
,夹角的范围![]()
针与任意一根平行线相交需满足的条件为![]() ,其中
,其中![]() 为针中心点位置到平行线的距离,l为针的长度,如下图所示:
为针中心点位置到平行线的距离,l为针的长度,如下图所示:
把针投掷到许多条间距为a的平行线中,针中心点与平行线的距离为![]() ,a为平行线的间距,针是随机投掷到平面上,所以针与平行线距离的概率密度函数为
,a为平行线的间距,针是随机投掷到平面上,所以针与平行线距离的概率密度函数为![]()
把针投掷到许多条间距为a的平行线中,针与平行线的夹角为![]() ,所以针与平行线夹角
,所以针与平行线夹角![]() 的概率密度函数为
的概率密度函数为![]()
联合概率密度函数为![]() ,根据联合概率密度可求出针与平行线之间相交的概率为:
,根据联合概率密度可求出针与平行线之间相交的概率为:
从上面的公式可以看出,只要知概率P就可以求出圆周率![]() ,下面我们采用蒙特卡洛随机投点法求出概率P,从而求出圆周率。
,下面我们采用蒙特卡洛随机投点法求出概率P,从而求出圆周率。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 用蒙特卡洛方法计算圆周率π
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function circumference_ratio
N=30; %重复试验的次数
needles=10000; %每次实验投掷针的数目
length=0.6; %针的长度,平行线间距为1
PAI=zeros(1,N); %存储每次实验结果数值
for k=1:N
PAI(k)=buffon(length,needles); %求圆周率
end
PAI_ave=mean(PAI) %对多次的实验取平均值
figure
hold on;
box on;
plot(PAI);
line([0,N],[PAI_ave,PAI_ave],'LineWidth',3,'Color','g');
xlabel('k');
ylabel('π的估计值');
function pai=buffon(length,N)
frq=0;
for k=1:N
distance = unifrnd(0,0.5); %生成针中心点与平行线之间的间距
angle = unifrnd(0,pi); %生成针与平行线的夹角
if (distance <= (length*sin(angle)/2) ) %判断针是否与平行线相交
frq=frq+1; %统计相交的数量
end
end
p=frq/N; %求取相交的概率
pai=2*length/p; %计算圆周率估计圆周率值:
![]()
多次实验结果及其均值,图中蓝色部分曲线是每次实验的数值,绿色部分是实验的平均值如下图所示:
4、蒙特卡洛定积分计算
假设要计算得定积分为:![]() ,该公式中a、b为有限值被积分函数为
,该公式中a、b为有限值被积分函数为![]() 为连续变量
为连续变量![]() 的概率密度函数,因此
的概率密度函数,因此![]() 必须满足一下条件:
必须满足一下条件:
(1) ![]() 非负数
非负数
从上述的公式中可以看出![]() 就是一个积分,并且满足
就是一个积分,并且满足![]() {
{![]() }
}
利用蒙特卡洛原理给定一个满足上述(1)(2)条件的概率密度函数![]() ,如何求取出概率积分
,如何求取出概率积分![]()
(1)首先产生服从![]() 分布的随机数m
分布的随机数m
(2)然后统计落在{![]() }区域的随机数n
}区域的随机数n
(3)求得落在{![]() }区域的概率为
}区域的概率为![]()
被积函数一般不满足公式(2)条件,所以需要对被积分函数进行变换,假设被积函数为![]() 。
。
设定一定上限值M,设![]() ,如下图所示把一般的被积函数变换成概率密度函数,方形的面积为
,如下图所示把一般的被积函数变换成概率密度函数,方形的面积为![]() ,而函数
,而函数![]() 所包围阴影部分区域面积的值即为函数的积分值。
所包围阴影部分区域面积的值即为函数的积分值。
根据上述可以求出阴影部分的概率![]() ,如下所示:
,如下所示:
所以:![]()
![]()
![]() ,从这个公式可以得出我们只要利用随机投点计算出n与m的比值就可以间接算出函数
,从这个公式可以得出我们只要利用随机投点计算出n与m的比值就可以间接算出函数![]() 的积分值,其中m为蒙特卡洛随机投点的数目,n为落在
的积分值,其中m为蒙特卡洛随机投点的数目,n为落在![]() 区域内的数目。
区域内的数目。
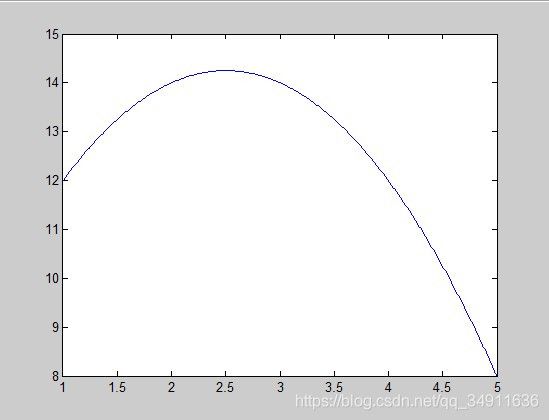
例子:求函数![]() ,在[1,5]区间内的积分,通过积分运算很容易算出该函数的积分值为50.66666,
,在[1,5]区间内的积分,通过积分运算很容易算出该函数的积分值为50.66666,![]() 函数曲线如下所示:
函数曲线如下所示:
(1)又上图我们可知函数在[1,5]区间的最大值小于15,所以我们设定![]() ,
,![]()
(3)在![]() 区域内随机投掷m个点,并统计落在
区域内随机投掷m个点,并统计落在![]() 区域内的随机点数n。
区域内的随机点数n。
利用matlab编程如下:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 利用蒙特卡洛计算定积分
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
a=1; %设定积分下限
b=5; %设定积分上限
M=15; %设置M值
N=100000; %产生随机点的数目
freq=0; %统计落在函数区域内的随机点数
for i=1:N
x=unifrnd(a,b); %产生[a,b]区间的随机数
v=unifrnd(0,M); %产生[0,M]区间的随机数
if (-power(x,2) + 5*x + 8) >= v %判断随机点数是否落在函数内部
freq=freq+1; %统计数目
end
end
p=freq/N; %计算落在函数区域内部的概率
result=p*(b-a)*M %求出函数的积分值计算出来的结果:
5、平均值法求取函数的积分值
假设一组同分布分布并且独立的随机变量{![]() },随机变量{
},随机变量{![]() }概率密度函数为
}概率密度函数为![]() ,令
,令![]() 那么{
那么{![]() }也是一组同分布并且相互独立的随机变量,现对函数
}也是一组同分布并且相互独立的随机变量,现对函数![]() 的
的
选择抽样概率密度函数![]() 需要满足以下条件
需要满足以下条件
(1) 在区间[a,b]当![]() 时,
时,![]()
例子:以上一个例题为例,求函数![]() ,在[1,5]区间内的积分,
,在[1,5]区间内的积分,![]()
在区间[a,b]之间独立同分布均匀采样,![]()
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 利用蒙特卡洛平均法计算定积分
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
a=1; %积分下限
b=5; %积分上限
N=10000; %采样次数
sum=0; %求和
xrandnum = unifrnd(a,b,1,N); %利用unifrnd在区间[a,b]生成1xN矩阵的N个随机数
for ii=1:N
%对函数-x^2 + 5x +8进行采样
sum = sum - power(xrandnum(1,ii),2) + 5*xrandnum(1,ii) + 8;
end
result = (b-a)*(sum/N) %求和计算计算积分值结果如下所示,该结果与前面结算的结果一致,与真实值非常接近
6、重要抽样法
重要性采样(Importance Sampling)是已知被积函数的一些分布信息而采用的一种缩减方差的策略,我们假设一个简单的例子:
![]()
对上面的函数我们采用蒙特卡洛法估计它的积分,选择区间[0, 1]之间的均匀分布作为它的随机数,那么存在绝大部分的采样点在区间[0.1, 1]之间,但是它对积分估计的贡献只有0.1,小部分采样点在区间[0, 0.1)之间,它对积分估计的贡献却非常的大,这种现象就会导致误差非常的大,简单提高采样数对估计量收敛的影响较小。那么,如果我们简单的选择一个采样策略:多采样区间[0, 0.1)的样本点,少采样[0.0,1]的样本点,这就违背了蒙特卡洛法的本质,产生的统计结果就没有任何意义。蒙特卡洛法的核心是根据某一概率分布来随机采样,那么根据被积函数曲线规律来设计类似的概率密度来进行采样,这就符合蒙特卡洛积分的要求,也就是重要性采样的核心。所以重要抽样法是要选择与被积函数![]() 密度函数较为相似的概率密度
密度函数较为相似的概率密度![]() ,如下例子所示:
,如下例子所示:
函数![]() ,泰勒展开式
,泰勒展开式![]() ,取一个近似的密度函数
,取一个近似的密度函数![]() 。根据第5节“平均法求取函数的积分值”
。根据第5节“平均法求取函数的积分值”![]() 的积分值近似为:
的积分值近似为:
而![]() 的分布函数为:
的分布函数为:
![]()
对概率密度的分布函数![]() 的变量x和因变量y进行变换,得到
的变量x和因变量y进行变换,得到![]()
利用MATLAB模拟步骤及其MATLAB实现:
(1)产生n个区间[0,1]随机数使![]()
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 利用重采样法计算定积分
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
a=0; %积分区间下限
b=1; %积分区间上限
N=10000; %采样点数
sum=0; %求积分和
xrandnum = -1 + sqrt(1+3.*unifrnd(a,b,1,N)); %利用设定的概率密度函数的分布函数生成采样点
for ii=1:N
sum=sum+exp(xrandnum(1,ii))/(1+ xrandnum(1,ii)); %积分值求和
end
result=1.5*sum/N %积分值求和
输出结果:
读到这边相信大家可能会有个疑问?为什么需要重新设定概率密度函数,然后求取概率密度函数的分布函数的随机分布变量,再间接利用分布函数求取积分函数变量的采样点。通过这种方法求取积分函数的采样点和直接求取积分函数变量的采样点有什么不一样?请看下面的这张图,下面这张图描述了积分函数![]() 在[0,1]区间的曲线(图中最上面的那条蓝色曲线)、重采样概率密度函数
在[0,1]区间的曲线(图中最上面的那条蓝色曲线)、重采样概率密度函数![]() 在[0,1]区间的曲线(图中中间的那条绿色曲线)、概率密度函数
在[0,1]区间的曲线(图中中间的那条绿色曲线)、概率密度函数![]() 的分布函数
的分布函数![]() 在[0,1]区间的曲线(图中下面的那条红色曲线)。
在[0,1]区间的曲线(图中下面的那条红色曲线)。
从积分函数![]() 的曲线(图中最上面的那条蓝色曲线)我们可以看出曲线越往右侧越呈现较大幅度的增长,所以曲线越往右侧对积分值的贡献越大,为了能够更加接近真实值,在采样时我们希望右侧的采样点更加密集。这时候我们就需要设定一个概率密度函数与积分函数的概率密度相接近,然后利用随机函数生成概率密度函数的分布函数的随机数,再利用分布函数映射(公式(2))间接求取积分函数的采样点,这样子求取出来的采样点在积分函数的右侧相对比较密集。如下图的
的曲线(图中最上面的那条蓝色曲线)我们可以看出曲线越往右侧越呈现较大幅度的增长,所以曲线越往右侧对积分值的贡献越大,为了能够更加接近真实值,在采样时我们希望右侧的采样点更加密集。这时候我们就需要设定一个概率密度函数与积分函数的概率密度相接近,然后利用随机函数生成概率密度函数的分布函数的随机数,再利用分布函数映射(公式(2))间接求取积分函数的采样点,这样子求取出来的采样点在积分函数的右侧相对比较密集。如下图的![]() 的曲线,其y轴为分布函数值,我们对分布函数取均匀等间距的采样点(在图中我们假设10个采样点每个采样点间距为0.1),然后我们通过分布函数把y轴上的采样点映射到x轴上,此时,我们可以看出映射到x轴的采样点右侧明显比较密集而往左侧就越来越稀疏,这个x轴的采样点符合积分函数的采样特点,我们再把x轴上的采样点带入公式(3)计算出积分函数
的曲线,其y轴为分布函数值,我们对分布函数取均匀等间距的采样点(在图中我们假设10个采样点每个采样点间距为0.1),然后我们通过分布函数把y轴上的采样点映射到x轴上,此时,我们可以看出映射到x轴的采样点右侧明显比较密集而往左侧就越来越稀疏,这个x轴的采样点符合积分函数的采样特点,我们再把x轴上的采样点带入公式(3)计算出积分函数![]() 的值。
的值。
![]()






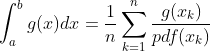
![E[G_{n}(X))] = E[{\frac{1}{n}}\sum_{k=1}^{n}\frac{g(X_{k})}{pdf(X_{k})}]](http://img.e-com-net.com/image/info8/8a353d114d134a13ad721c0b3a370aff.gif)
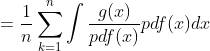

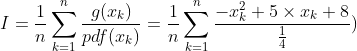

![g(x)=\begin{cases} & \text{99.9 } x\subset [0,0.1) \\ & \text{ 0.1 } x\subset [0.1,1] \end{cases}](http://img.e-com-net.com/image/info8/e4f6533f8ce54b4fb1edf20d89e7b67c.gif)

