计算智能课程设计报告
点击领取实验报告
计算智能课程设计报告
-
-
实验一:基于感知机的鸢尾花分类
-
- 一、实验题目:基于感知机的鸢尾花分类
- 二、实验目的
- 三、实验内容
- 四、实验结果与分析
实验二:以人事招聘为例的误差反向传播算法
-
- 一、实验题目: 以人事招聘为例的误差反向传播算法
- 二、实验目的
- 三、实验内容
- 四、实验结果与分析
- 五、小结与心得体会
实验三:基于神经网络的手写数字识别
-
- 一、实验题目: 基于神经网络的手写数字识别
- 二、实验目的
- 三、实验内容
- 关键源代码
- 四、实验结果与分析
- 五、小结与心得体会
实验四:基于传递闭包的模糊聚类
-
- 一、实验题目: 基于传递闭包的模糊聚类
- 二、实验目的
- 三、实验内容
- 关键源代码
- 四、实验结果与分析
实验五:遗传算法求解无约束单目标优化问题
-
- 一、实验题目: 遗传算法求解无约束单目标优化问题
- 二、实验目的
- 三、实验内容
- 关键源代码
- 实验结果与分析
-
实验一:基于感知机的鸢尾花分类
一、实验题目:基于感知机的鸢尾花分类
二、实验目的
利用感知机算法对鸢尾花种类进行分类,要求熟悉感知机算法,掌握利用Python实现机器学习算法的一般流程,了解scikit-learn机器学习库的使用。
三、实验内容
实验原理
感知器算法是非常好的二分类在线算法。该算法求取一个分离超平面,超平面由w∈R 参数化并用来预测。对于一个样本x,感知器算法通过计算y=(wx)预测样本的标签。最终的预测标签通过计算sign(y)来实现。算法仅在预测错误时修正权值w 。如果正确的标签是 y =1,那么权值修正为w +x;如果y =-1 ,权值变为w -x ,可以总结为 w←w +yx;需要注意的是在预测后,尽管算法不能保证修正后的预测准则会正确分类目前的样本,但在目前样本上的分离超平面的间隔会增加,即算法是保守的不是主动的
算法/程序流程图
步骤和方法
设给定一个增广的训练式集{x1,x2… xN},其中每个模式类别已知,它们分属于w1类和w2类。(1)置步数k=1,令增量p=某正常数,分别赋给初始增广权向量w1的各分量较小的任意值。
(2)输入训练模式xk,计算判别函数值wkxk
(3)调整增广权矢量,规则是
–如果xk∈w1和w(k)xk ≤0,则w(k + 1) = w(k)+ pxk
–如果xk∈w2和w(k)xk ≥0,则w(k + 1) = w(k)- pxk
–如果xk∈w1和w(k)xk >0或如果xk∈w2和w(k)xk <0则w(k+ 1) = w(k)。
(4)如果k
(1)算法初始化
X=np.c_[np.ones(100),iris.data[:100,2:4]] #输入 X
T=iris.target[:100].reshape(100,1) #真值 T
T[T!=1] = -1 #将 0 用-1 表示,以契合 sign 函数
W = np.array([[-7], #权值初始化,3 行 1 列,即 w0 w1 w2
[1],
[1]])
lr = 1 # 学习率设置
(2)训练算法
def train():
global W
Y = np.sign(np.dot(X,W))
E = T - Y
delta_W = lr * (X.T.dot(E)) / X.shape[0]
W = W + delta_W
(3)主函数
# 训练 1000 次
for i in range(1000):
if(i==0): #特地画出未经训练的初始图像,以方便理解
draw()
plt.pause(5) #停留两秒,这是分类直线最初的位置,取决于 W 的初始值,是人为决定的超参数
train() #更新一次权值
draw() #画出更新一次权值后的图像
Y = np.sign(np.dot(X,W))
# .all()表示 Y 中的所有值跟 T 中所有值都对应相等,结果才为真
if(Y == T).all():
print('Finished')
# 跳出循环
break
四、实验结果与分析
1)考虑学习率的作用。修改示例代码,固定初始权值=(1,1,1),将学习率分别设定为1、0.5、0.1(组合1~3),程序在epoch 等于多少时实现分类?
(当学习率为1时,epoch为8) (当学习率为0.5时,epoch为9) (当学习率为0.1时,epoch为181)
原因:学习率越高,每步变化越大,,所以在比较少的步数之内就可以实现分类。但是如图所示,步数较越大,数据的边界距离分界线越远。0.1时,数据分界线与数据接触比较密切。
2)考虑初始权值的作用。修改示例代码,固定学习率=0.1,将初始权值分别设定为(-1,1,1)、(+1,-1,-1)、(1,-1,+1) 、(-1,+1,-1) (组合4~7),程序在epoch 等于多少时实现分类?
改变不同权值,但是学习率不改变的情况下,由图可以看出,epoch变化不大。
3)示例程序使用的是离散感知机还是连续感知机?如何判断?
这是离散感知机感知器(Perceptron)是由 Rosenblatt定义的具有单层神经计算单元的神经网络结构。实际上为一种前馈网络,同层内无互连,不同层间无反馈,由下层向上层传递,其输入、输出均为离散值,神经元对输入加权求和后,由阈值函数(激活函数)决定其输出。我们使用的感知机中,只是用了一个神经元。没有输出向量。(连续型感知机需要对比输出和输入向量)
根据激活函数来判断感知机是离散还是连续;本程序使用的激活函数是np.sign,该函数的定义域为R,当自变量大于0时,函数值为1;当自变量等于0时,函数值为0;当自变量小于0时,函数值为-1;由于f(0+)!=f(0-),所以函数不连续,所以感知机为离散感知机。
4)为什么在学习算法中要除以X.shape[0] ?示例程序采用的是批量下降还是逐一下降?是否属于随机下降?是否属于梯度下降?
shape[0]得到X的行数,表示有多少个数据,属于批量下降,因为每一步都对数组中所有数据除X.shape[0],得到平均值,得到的delta_W是对所有数据更改之后的变化量,所以是批量下降。
5)假设你在自然界找到了一朵鸢尾花,并测得它的花瓣长度为2.5cm,花瓣宽度为1cm,它属于哪一类?在draw()中已用plt.plot 画出这个’待预测点’。请观察1~7 这7 种组合中,感知机的判断始终一致么?这说明它受到什么因素的影响?
根据图像可知是变色鸢尾花,
(在步长(学习率)变化后分类会产生变化,但是初始权值变化后,分类不会发生变化,所以,受学习率影响)
6)修改示例代码,将变色鸢尾的数据替换为维吉尼亚鸢尾,再进行分类。即横轴为花瓣长度,纵轴为花瓣宽度,数据为Setosa 山鸢尾+Virginica 维吉尼亚鸢尾。
X1 = np.c_[np.ones(100), iris.data[:100, 2:4]]
X2 = iris.data[:100,0:1]#选萼片长度
X = np.c_[X1, X2]#100行4列
W = np.array([[1],
[1],
[1],
[1]])#加入萼片长度的权值
7)【可选】目前感知机只有两个输入+偏置,如果有三个输入(比如增加萼片长度作为输入),程序应如何修改(可以不画图)?
实验二:以人事招聘为例的误差反向传播算法
一、实验题目: 以人事招聘为例的误差反向传播算法
二、实验目的
理解多层神经网络的结构和原理,掌握反向传播算法对神经元的训练过程,了解反向传播公式。
通过构建BP 网络实例,熟悉前馈网络的原理及结构。
三、实验内容
实验原理
对每一层依次求对权值的偏导数,构成目标函数对权值的梯度,网络权重再依次完成更新调整。依此往复、直到输出达到目标值完成训练。该算法可以总结为:利用输出误差推算前一层的误差,再用推算误差算出更前一层的误差,直到计算出所有层的误差估计。
算法/程序流程图
步骤和方法
对每一层依次求对权值的偏导数,构成目标函数对权值的梯度,网络权重再依次完成更新调整。依此往复、直到输出达到目标值完成训练。该算法可以总结为:利用输出误差推算前一层的误差,再用推算误差算出更前一层的误差,直到计算出所有层的误差估计。
#### 关键源代码
(1).初始化
4. # 输入数据 1 行 2 列
5. X = np.array([[1,0.1]])
6.
7. # 标签,也叫真值,1 行 1 列
8. T = np.array([[1]])
9.
10. # 定义一个 2 隐层的神经网络:2-2-2-1
11. # 输入层 2 个神经元,隐藏 1 层 2 个神经元,隐藏 2 层 2 个神经元,输出层 1 个神经元
12.
13. # 输入层到隐藏层 1 的权值初始化,2 行 2 列
14. W1 = np.array([[0.8,0.2],
15. [0.2,0.8]])
16. # 隐藏层 1 到隐藏层 2 的权值初始化,2 行 2 列
17. W2 = np.array([[0.5,0.0],
18. [0.5,1.0]])
19. # 隐藏层 2 到输出层的权值初始化,2 行 1 列
20. W3 = np.array([[0.5],
21. [0.5]])
22.
23.
24. # 初始化偏置值
25. # 隐藏层 1 的 2 个神经元偏置
26. b1 = np.array([[-1,0.3]])
27. # 隐藏层 2 的 2 个神经元偏置
28. b2 = np.array([[0.1,-0.1]])
29. # 输出层的 1 个神经元偏置
30. b3 = np.array([[-0.6]])
31. # 学习率设置
32. lr = 0.1
33. # 定义训练周期数 10000
34. epochs = 10000
35. # 每训练 1000 次计算一次 loss 值
36. report = 1000
37. # 将所有样本分组,每组大小为
38. batch_size = 1
40. # 定义 sigmoid 函数
41. def sigmoid(x):
42. return 1/(1+np.exp(-x))
43.
44. # 定义 sigmoid 函数导数
45. def dsigmoid(x):
46. return x*(1-x)
(2).更新权值
48. # 更新权值和偏置值
49. def update():
50. global batch_X,batch_T,W1,W2,W3,lr,b1,b2,b3
51.
52. # 隐藏层 1 输出
53. Z1 = np.dot(batch_X,W1) + b1
54. A1 = sigmoid(Z1)
55.
56. # 隐藏层 2 输出
57. Z2 = (np.dot(A1,W2) + b2)
58. A2 = sigmoid(Z2)
59.
60. # 输出层输出
61. Z3=(np.dot(A2,W3) + b3)
62. A3 = sigmoid(Z3)
64. # 求输出层的误差
65. delta_A3 = (batch_T - A3)
66. delta_Z3 = delta_A3 * dsigmoid(A3)
67.
68. # 利用输出层的误差,求出偏导(即隐藏层 2 到输出层的权值改变) # 由于一次计算了多个样本,所以需要求平均
69. delta_W3 = A2.T.dot(delta_Z3) / batch_X.shape[0]
70. delta_B3 = np.sum(delta_Z3, axis=0) / batch_X.shape[0]
71.
72. # 求隐藏层 2 的误差
73. delta_A2 = delta_Z3.dot(W3.T)
74. delta_Z2 = delta_A2 * dsigmoid(A2)
75.
76. # 利用隐藏层 2 的误差,求出偏导(即隐藏层 1 到隐藏层 2 的权值改变) # 由于一次计算了多个样本
所以需要求平均
77. delta_W2 = A1.T.dot(delta_Z2) / batch_X.shape[0]
78. delta_B2 = np.sum(delta_Z2, axis=0) / batch_X.shape[0]
79.
80. # 求隐藏层 1 的误差
81. delta_A1 = delta_Z2.dot(W2.T)
82. delta_Z1 = delta_A1 * dsigmoid(A1)
83.
84. # 利用隐藏层 1 的误差,求出偏导(即输入层到隐藏层 1 的权值改变) # 由于一次计算了多个样本,
所以需要求平均
85. delta_W1 = batch_X.T.dot(delta_Z1) / batch_X.shape[0]
86. delta_B1 = np.sum(delta_Z1, axis=0) / batch_X.shape[0]
87.
88. # 更新权值
89. W3 = W3 + lr *delta_W3
90. W2 = W2 + lr *delta_W2
91. W1 = W1 + lr *delta_W1
92.
93. # 改变偏置值
94. b3 = b3 + lr * delta_B3
95. b2 = b2 + lr * delta_B2
96. b1 = b1 + lr * delta_B1
(3).训练模型
103. # 训练模型
104. for idx_epoch in range(epochs):
105.
106. for idx_batch in range(max_batch):
107. # 更新权值
108. batch_X = X[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
109. batch_T = T[idx_batch*batch_size:(idx_batch+1)*batch_size, :]
110. update()
111. # 每训练 5000 次计算一次 loss 值
112. if idx_epoch % report == 0:
113. # 隐藏层 1 输出
114. A1 = sigmoid(np.dot(X,W1) + b1)
115. # 隐藏层 2 输出
116. A2 = sigmoid(np.dot(A1,W2) + b2)
117. # 输出层输出
118. A3 = sigmoid(np.dot(A2,W3) + b3)
119. # 计算 loss 值
120. print('A3:',A3)
121. print('epochs:',idx_epoch,'loss:',np.mean(np.square(T - A3) / 2))
122. # 保存 loss 值
123. loss.append(np.mean(np.square(T - A3) / 2))
125. # 画图训练周期数与 loss 的关系图
126. plt.plot(range(0,epochs,report),loss)
127. plt.xlabel('epochs')
128. plt.ylabel('loss')
129. plt.show()
130.
131. # 隐藏层 1 输出
132. A1 = sigmoid(np.dot(X,W1) + b1)
133. # 隐藏层 2 输出
134. A2 = sigmoid(np.dot(A1,W2) + b2)
135. # 输出层输出
136. A3 = sigmoid(np.dot(A2,W3) + b3)
137. print('output:')
138. print(A3)
139.
140. # 因为最终的分类只有 0 和 1,所以我们可以把
141. # 大于等于 0.5 的值归为 1 类,小于 0.5 的值归为 0 类
142. def predict(x):
143. if x>=0.5:
144. return 1
145. else:
146. return 0
四、实验结果与分析
1)如果去掉总裁这一层,相应张三的样本修改为(1.0,0.1,1.0,1.0),分别对应张三的学习成绩、张三的实践成绩、张三的工作能力真值、张三的工作态度真值,代码应该如何修改?
2)如果增加一个样本,李四(0.1,1.0,0),分别对应李四的学习成绩,李四的实践成绩,李四被招聘可能性的真值,代码应该如何修改?此时是一个样本计算一次偏导、更新一次权值,还是两个样本一起计算一次偏导、更新一次权值?(提示:注意batch_size 的作用)
此时是两个样本一起计算一次偏导、更新一次权值
3)样本为张三[1,0.1,1]、李四[0.1,1,0]、王五[0.1,0.1,0]、赵六[1,1,1],请利用batch_size 实现教材279 页提到的“批量梯度下降”、“随机梯度下降”和“小批量梯度下降”,请注意“随机梯度下降”和“小批量梯度下降”要体现随机性。
-
批量梯度下降
-
随机批量梯度下降
-
小批量梯度下降
结果:收敛效果的优越性 随机梯度下降 > 小批量梯度下降 > 批量梯度下降
4 ) 【选做】本例中输入向量、真值都是行向量, 请将它们修改为列向量, 如X = np.array([[1,0.1]])改为X = np.array([[1],[0.1]]),请合理修改其它部分以使程序得到与行向量时相同的结果。
将所有关于X的地方转置
结果:左边为行向量结果,右边为列向量结果
五、小结与心得体会
通过本实验,了解了连续型多感知机所能处理的问题比单感知机要复杂。知道了多感知机输出与当感知机输出在编程时表达的异同;深深理解了BP算法在实际求解delta值时的易用性与方便性;理解并掌握了3种梯度下降方法的解决实际问题时该如何实验;掌握了如何把行向量编程转换为列向量编程。
实验三:基于神经网络的手写数字识别
一、实验题目: 基于神经网络的手写数字识别
二、实验目的
掌握神经网络的设计原理,熟练掌握神经网络的训练和使用方法,能够使用Python语言,针对手写数字分类的训练和使用,实现一个三层全连接神经网络模型。具体包括:
实现三层神经网络模型来进行手写数字分类,建立一个简单而完整的神经网络工程。通过本实验理解神经网络中基本模块的作用和模块间的关系,为后续建立更复杂的神经网络实验奠定基础。
利用Python实现神经网络基本单元的前向传播(正向传播)和反向传播,加深对神经网络中基本单元的理解,包括全连接层、激活函数、损失函数等基本单元。
利用Python实现神经网络的构建和训练,实现神经网络所使用的梯度下降算法,加深对神经网络训练过程的理解。
三、实验内容
实验原理
一个完整的神经网络通常由多个基本的网络层堆叠而成。本实验中的三层全连接神经网络由三个全连接层构成,在每两个全连接层之间插入 ReLU 激活函数以引入非线性变换,最后使用 Softmax 层计算交叉熵损失,如图 2.1 所示。因此本实验中使用的基本单元包括全连接层、ReLU 激活函数、Softmax 损失函数。
算法/程序流程图
关键源代码
1.)数据集
2)总体设计
1)数据加载模块:从文件中读取数据,并进行预处理,其中预处理包括归一化、维度变换等 处理。如果需要人为对数据进行随机数据扩增,则数据扩增处理也在数据加载模块中实现。
1. def load_mnist(self, file_dir, is_images = 'True'):
2. bin_file = open(file_dir, 'rb')
3. bin_data = bin_file.read()
4. bin_file.close()
5. # 分析文件头部
6. if is_images: # 读取图像数据
7. fmt_header = '>iiii'
8. magic, num_images, num_rows, num_cols = struct.unpack_from(fmt_header, bin_data, 0
9. else: # 读取标记数据
10. fmt_header = '>ii'
11. magic, num_images = struct.unpack_from(fmt_header, bin_data, 0)
12. num_rows, num_cols = 1, 1
13. data_size = num_images * num_rows * num_cols
14. mat_data = struct.unpack_from('>' + str(data_size) + 'B', bin_data, struct.calcsize(fm t_header))
15. mat_data = np.reshape(mat_data, [num_images, num_rows * num_cols])
16. print('Load images from %s, number: %d, data shape: %s' % (file_dir, num_images, str(m at_data.shape)))
17. return mat_data
TRAIN_DATA = "train-images-idx3-ubyte"
TRAIN_LABEL = "train-labels-idx1-ubyte"
TEST_DATA = "t10k-images-idx3-ubyte" TEST_LABEL = "t10k-labels-idx1-ubyte"
2)基本单元模块:实现神经网络中不同类型的网络层的定义、前向传播、反向传播等功能。
1. class FullyConnectedLayer(object):
2. def init (self, num_input, num_output): # 全连接层初始化
3. self.num_input = num_input
4. self.num_output = num_output
5. print('\tFully connected layer with input %d, output %d.' % (self.num_input, self. num_output))
6. def init_param(self, std=0.01): # 参数初始化
7. self.weight = np.random.normal(loc=0.0, scale=std, size=(self.num_input, self.num_ output))
8. self.bias = np.zeros([1, self.num_output])
9. def forward(self, input): # 前向传播计算
10. start_time = time.time()
11. self.input = input
12. # TODO:全连接层的前向传播,计算输出结果 提示:公式 2.1,矩阵乘法 np.matmul
13. self.output = np.matmul(self.input,self.weight) + self.bias #bias不能加转置(公式2-3有错误)
14. return self.output
15. def backward(self, top_diff): # 反向传播的计算 大水漫灌,top_diff 就是上一层房间的海水
16. # TODO:全连接层的反向传播,计算参数梯度和本层损失
17. self.d_weight = np.dot(self.input.T,top_diff) # 提示:公式 2.4
18. self.d_bias = np.dot(top_diff.T,np.ones((self.input.shape[0],1)))
19. bottom_diff = np.dot(top_diff,self.weight.T
20. return bottom_diff # 大水漫灌,bottom_diff 就是传到下一层房间的海水
21. def update_param(self, lr): # 参数更新
22. # TODO:对全连接层参数利用参数进行更新 提示:公式 2.14
23. self.weight = self.weight-lr*self.d_weight
24. self.bias = self.bias-lr*self.d_bias.T
25. def load_param(self, weight, bias): # 参数加载
26. assert self.weight.shape == weight.shape
27. assert self.bias.shape == bias.shape
28. self.weight = weight
29. self.bias = bias
30. def save_param(self): # 参数保存
31. return self.weight, self.bias
3)网络结构模块:利用基本单元模块建一个完整的神经网络。
1. class MNIST_MLP(object):
2. def init (self, batch_size=100, input_size=784, hidden1=32, hidden2=16, out_classes=10, lr=0.01, max_epoch=2, print_iter=100):
3. # 神经网络初始化
4. self.batch_size = batch_size
5. self.input_size = input_size
6. self.hidden1 = hidden1
7. self.hidden2 = hidden2
8. self.out_classes = out_classes
9. self.lr = lr
10. self.max_epoch = max_epoch
11. self.print_iter = print_iter
12. def build_model(self): # 建立网络结构
13. # TODO:建立三层神经网络结构
14. print('Building multi-layer perception model...')
15. self.fc1 = FullyConnectedLayer(self.input_size, self.hidden1)
16. self.relu1 = ReLULayer()
17. self.fc2 = FullyConnectedLayer(self.hidden1,self.hidden2)
self.relu2 = ReLULayer()
18. self.fc3 = FullyConnectedLayer(self.hidden2, self.out_classes)
19. self.softmax = SoftmaxLossLayer()
20. self.update_layer_list = [self.fc1, self.fc2, self.fc3]
21.
22. def init_model(self):
23. print('Initializing parameters of each layer in MLP...')
24. for layer in self.update_layer_list:
25. layer.init_param()
4)网络训练(training)模块:用训练集对神经网络进行训练。对建立的神经网络结构,实 现神经网络的前向传播、神经网络的反向传播、对神经网络进行参数更新、保存神经网络参数等基本操作,以及训练函数主体。
1. def forward(self, input): # 神经网络的前向传播
2. # TODO:神经网络的前向传播
3. h1 = self.fc1.forward(input)
4. h1 = self.relu1.forward(h1)
5. h2 = self.fc2.forward(h1)
#h2 = self.relu2.forward(h2)
6. prob = self.softmax.forward(h3)
7. return prob
8.
9. def backward(self): # 神经网络的反向传播
10. # TODO:神经网络的反向传播
11. dloss = self.softmax.backward()
5)网络推断(inference)模块:使用训练得到的网络模型,对测试样本进行预测(也称为 测试或推断)。具体操作包括加载训练得到的模型参数、神经网络的前向传播等。
1. def load_model(self, param_dir): # 加载神经网络权值
2. print('Loading parameters from file ' + param_dir)
3. params = np.load(param_dir, allow_pickle=True).item()
4. self.fc1.load_param(params['w1'], params['b1'])
5. self.fc2.load_param(params['w2'], params['b2'])
6. self.fc3.load_param(params['w3'], params['b3'])
8. def evaluate(self): # 推断函数
9. pred_results = np.zeros([self.test_data.shape[0]])
10. start_time = time.time()
11. for idx in range(self.test_data.shape[0]//self.batch_size):
12. batch_images = self.test_data[idx*self.batch_size:(idx+1)*self.batch_size, :-1]
13. prob = self.forward(batch_images)
14. end = time.time()
15. pred_labels = np.argmax(prob, axis=1)
16. pred_results[idx*self.batch_size:(idx+1)*self.batch_size] = pred_labels
17. print("All evaluate time: %f"%(time.time()-start_time))
18. accuracy = np.mean(pred_results == self.test_data[:,-1])
19. print('Accuracy in test set: %f' % accuracy)
四、实验结果与分析
1)请在代码中有TODO的地方填空,将程序补充完整,在报告中写出相应代码,并给出自己的理解。
根据指导书的公式,以及代码上下文环境和自己的理解推断出需要填写的代码。
FullyConnectedLayer层:第一个空是填正向传播的输出,根据公式可以得到,正向输出等于输入与权值的点乘加偏置;第二问是填反向传播中权值、偏置和输入的梯度,根据公式有权值梯度为输入的的转置与输出的梯度的权值。同理按照公式可以得到偏置以及输入的梯度。第三个空是求出梯度后对权值以及偏置的更新,根据公式可以得到权值为旧的权值减去学习率乘以权值的梯度,同理求出更新后的偏置。
ReLU层:第一空是填正向输出,根据relu激活函数的特点,当输入小于0则输出等于0,否则输出就等于输入值。所以填 max(0,x(i));第二问是求反向传播中的输入的偏导,根据公式可以得到在输入非负下输入的偏导等于输出的偏导。
Softmax 损失层:第一问是求前向传播的损失函数,根据公式2.11有self.prob = input_exp/np.sum(input_exp,axis=1).reshape(-1,1);第二问是求损失函数对输入的偏导,根据公式可得到答案;
网络结构模块:根据3层网络结构 全连接->relu激活->全连接->relu激活->全连接->softmax损失函数可以很容易知道此处需要填写fc2以及relu2,在根据代码上下文便可知道填写内容。
网络训练模块:主要是完成训练过程各种参数的调整。在前向传播中,在求的损失函数的过程中,根据上面神经网络层的结构,要求2个全连接层以及relu层,根据代码上下文环境便知道第一问要填fc2和relu2;对于反向传播,可以类似分析得到第二问要填relu2和fc2的偏导。
2)mlp.load_data()执行到最后时,train_images、train_labels、test_images、test_labels 的维度是多少?即多少行多少列,用(x,y)来表示self.train_data 和 self.test_data 的维度是多少?
在程序中添加输出数据维度的代码,查看结果。
3)本案例中的神经网络一共有几层?每层有多少个神经元?如果要增加或减少层数,应该怎么做(简单描述即可不用编程)?如果要增加或减少某一层的节点,应该怎么做(简单描述)?如果要把 softmax 换成 sigmoid,应该怎么做(简单描述)?
①一共四层:1个输入层2个隐藏层和1个输出层;
②hidden1=256个神经元 ,hi dden2=128个神经元,输出层10个神经元;
③若要增加或者减少层数,在init函数的参数里增加层数的参数,然后再在build_model通过self.fc =FullyConnecte dLayer(参数)把新增加的层数构建到网络;删除就先在init里把相要删除的层的参数删除,在build_model把构建了的相应的层删掉。
④增加或减少某一层的节点,只需要修改init函数的节点参数,比如要修改第一个隐藏层的神经元数,只需要修改hidden1的数值。
⑤把softmax 换成 sigmoid,首先要在layer1文件里把softmaxlossLayer代码改成sigmoid的逻辑代码;然后在minst_mlp_cpu文件里导入的sigmiodlayer,删掉softmaxlossLayer;最后在build_model里把self.softmax = SoftmaxLossLayer()改为sigmoid代码。
4)在 train()函数中,max_batch = self.train_data.shape[0] // self. batc h_size 这一句的意义是什么?self.shuffle_data()的意义是什么?
①这一句的意义是将60000行样本数据分组,每组大小为100个,一共600组。
②因为每一batch并没包含训练样本的全部数据。在每一样本中,loss求的是平均值,打乱的好处在于,防止数据按一定规律排列,可以更多的训练不同的数据并对其求平均值,这样的样本也更加接近真实分布。
5)最终evaluate()函数输出的 Accuracy in test set 是多少?请想办法提高该数值。
在hid1为256,hid2为128,epoch为10时,总共跑了三十几秒,最后正确率为98.17%。
成功率为98.15 ± 0.02 %
五、小结与心得体会
这个题要有耐心,根据公式一步一步推导,并且要学习很多新的python语法和函数,要慢慢来。
实验四:基于传递闭包的模糊聚类
一、实验题目: 基于传递闭包的模糊聚类
二、实验目的
掌握建立模糊等价矩阵的方法,会求传递闭包矩阵;掌握利用传递闭包进行模糊聚类的一般方法;
会使用Python进行模糊矩阵的有关运算。
三、实验内容
实验原理
关系的闭包的定义:
关系的闭包运算是关系上的一元运算,它把给出的关系R扩充成一个新关系R’,使R’具有一定的性质,且所进行的扩充又是最“节约”的。比如自反闭包,相当于把关系R对角线上的元素全改成1,
其他元素不变,这样得到的R’是自反的,且是改动次数最少的,即是最“节约”的。
算法/程序流程图
步骤和方法
从模糊相似矩阵得到传递闭包,采用的方法是平方法,具体方法是:把一个相似矩阵R进行自乘操作,得到R2并且检验R2是否满足传递性,如果R2满足传递性则停止,否则计算R4并且检验R4是否满足传递性,如果R4满足传递性则停止,否则计算R^8……,依此类推。这里的自乘操作是模糊集合下的算子,即用模糊集合操作的“交”和“并”取代了原来矩阵操作中的“乘”和“加”操作。理论上已经证明,该相乘操作只需要进行最多log2n + 1次,就可以得到t®
关键源代码
5. def MaxNormalization(a):
6. """
7. 采用最大值规格化法将数据规格化为
8. """
9. c = np.zeros_like(a, dtype=float)
10. for j in range(c.shape[1]): # 遍历 c 的列
11. for i in range(c.shape[0]): # 遍历 c 的列
12. c[i, j] = a[i, j]/np.max(a[:, j])
13. return c
14.
15. def FuzzySimilarMatrix(a):
16. """
17. 用最大最小法构造得到模糊相似矩阵
18. """
19. a = MaxNormalization(a) # 用标准化后的数据
20. c = np.zeros((a.shape[0], a.shape[0]), dtype=float)
21. mmax = []
22. mmin = []
23. for i in range(c.shape[0]): # 遍历 c 的行
24. for j in range(c.shape[0]): # 遍历 c 的行
25. mmax.extend([np.fmax(a[i, :], a[j, :])]) # 取 i 和和 j 行的最大值,即求 i 行和 j 行的
并
26. mmin.extend([np.fmin(a[i, :], a[j, :])]) # 取 i 和和 j 行的最大值,即求 i 行和 j 行的交
27. for i in range(len(mmax)):
28. mmax[i] = np.sum(mmax[i]) # 求并的和
29. mmin[i] = np.sum(mmin[i]) # 求交的和
30. mmax = np.array(mmax).reshape(c.shape[0], c.shape[1]) #变换为与 c 同型的矩阵
31. mmin = np.array(mmin).reshape(c.shape[0], c.shape[1]) #变换为与 c 同型的矩阵
32. for i in range(c.shape[0]): # 遍历 c 的行
33. for j in range(c.shape[1]): # 遍历 c 的列
34. c[i, j] = mmin[i, j]/mmax[i, j] # 赋值相似度
35. return c
51. def TransitiveClosure(a):
52. """
53. 平方法合成传递闭包
54. """
55. a = FuzzySimilarMatrix(a) # 用最大最小法构造得到模糊相似矩阵
56. c = a
57. while True:
58. m = c
59. c = MatrixComposition(MatrixComposition(a, c), MatrixComposition(a, c))
60. if (c == m).all(): # 闭包条件
61. return np.around(c, decimals=2) # 返回传递闭包,四舍五入,保留两位小数
62. break
63. else:
64. continue
65.
66. def CutSet(a):
67. """
68. 水平截集
69. """
70. a = TransitiveClosure(a) # 用传递闭包
71.
72. return np.sort(np.unique(a).reshape(-1))[::-1]
四、实验结果与分析
1)为什么按最大最小法得到的一定是一个方阵?且一定是自反方阵?且一定是对称方阵?
采用最大最小法构造得到模糊相似矩阵,为了建立模糊相似矩阵,引入相似系数r_ij表示两个样本x_i与x_j之间的相似程度,组成模糊相似矩阵R= 〖(r_ij)〗_(n×n)
。建立方法有最大最小法、算术平均最小法、几何平均最小法等。最大最小法的具体公式是:
算术平均最小法的具体公式为:
模糊相似矩阵R= 〖(r_ij)〗_(n×n)是表示r_i与r_j的关系的方阵,每个r_i要与其他所有的r产生关系,所以是一个二维数组方阵,数值是相似度。因为r_i与r_j的关系与r_j与r_i的关系是相同的,所以是对称矩阵,因为每个r_i与自己的关系都是1,所以是自反的。
2)为什么可以根据水平截集对数据进行分类?(提示:一个等价关系唯一确定一个划分)
由于模糊相似矩阵R本身已经是自反的、对称的,其传递闭包t®又是传递的,则t®一定是模糊等价矩阵,可以决定一个划分。a水平截集是指隶属度大于等于a的元素组成的集合,a水平截集是所有关系的集合。关系做了分类,可以根据a的特征函数判断数据的分类一个等价关系唯一确定一个划分,水平截集是在已经求的模糊等价矩阵后对这个模糊等价矩阵的划分,因为该矩阵具有等价关系,所以对其进行水平截集划分,必定有划分后数据集的并为全集,两两之间的交为空集。
3)请解释代码72 行中两个-1 的含义:
return np.sort(np.unique(a).reshape(-1))[::-1]
第一个 -1:reshape函数一个形状尺寸可以为-1。 在这种情况下,该值是根据数组的长度和其余维来推断的,根据a的维度来决定输出的维度。
第二个 -1:将排序后的水平截集逆序输出
4)在平方法的代码实现中,如何判断平方后的矩阵是否满足传递性?为什么可以这么判断?
计算MM,MM为M的子集的,在方阵对应的同行同列的位置,若对于M,该数为0,则对于MM,该数必为零,否则R不具有传递性。即:若M中的a[i][j] == 0, 则必有MM中的c[i][j] == 0,将平方后的矩阵A与它再平方的新矩阵相与,如果相与后的矩阵与平方后的矩阵A相同,则具有传递性
5)请修改代码,将最大最小法替换为算术平均最小法。这会改变最终的聚类结果么?
算术平均最小法的具体公式为:
将公式修改为:
15. def FuzzySimilarMatrix(a):
16. """
17. 用最大最小法构造得到模糊相似矩阵
18. """
19. a = MaxNormalization(a) # 用标准化后的数据
20. c = np.zeros((a.shape[0], a.shape[0]), dtype=float)
21. mmax = []
22. mmin = []
23. for i in range(c.shape[0]): # 遍历 c 的行
24. for j in range(c.shape[0]): # 遍历 c 的行
25. mmax.extend([ (a[i, :] + a[j, :])]) # 取 i 和和 j 行的最大值,即求 i 行和 j 行的并
26. mmin.extend([np.fmin(a[i, :], a[j, :])]) # 取 i 和和 j 行的最大值,即求 i 行和 j 行的交
27. for i in range(len(mmax)):
28. mmax[i] = np.sum(mmax[i]) # 求并的和
29. mmin[i] = np.sum(mmin[i]) # 求交的和
30. mmax = np.array(mmax).reshape(c.shape[0], c.shape[1]) #变换为与 c 同型的矩阵
31. mmin = np.array(mmin).reshape(c.shape[0], c.shape[1]) #变换为与 c 同型的矩阵
32. for i in range(c.shape[0]): # 遍历 c 的行
33. for j in range(c.shape[1]): # 遍历 c 的列
34. c[i, j] = 2*mmin[i, j]/mmax[i, j] # 赋值相似度
35. return c
结果没有改变
实验五:遗传算法求解无约束单目标优化问题
一、实验题目: 遗传算法求解无约束单目标优化问题
二、实验目的
理解遗传算法原理,掌握遗传算法的基本求解步骤,包括选择、交叉、变异等
学会运用遗传算法求解无约束单目标优化问题。
三、实验内容
实验原理
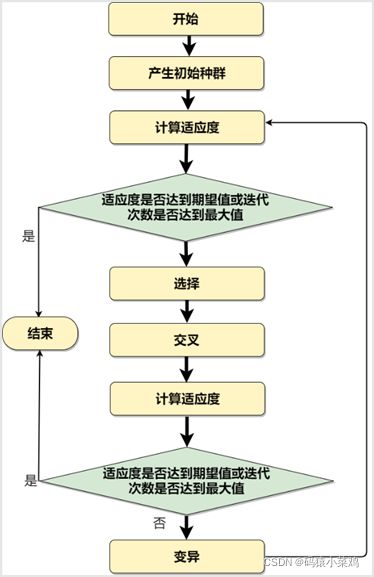
遗传算法是一种基于自然选择和群体遗传机理的搜索算法,它模拟了自然选择和自然遗传过程中的繁殖、杂交和突变现象.再利用遗传算法求解问题时,问题的每一个可能解都被编码成一个“染色体”,即个体,若干个个体构成了群体(所有可能解).在遗传算法开始时,总是随机的产生一些个体(即初始解),根据预定的目标函数对每一个个体进行评估,给出一个适应度值,基于此适应度值,选择一些个体用来产生下一代,选择操作体现了“适者生存”的原理,“好”的个体被用来产生下一代,“坏”的个体则被淘汰,然后选择出来的个体,经过交叉和变异算子进行再组合生成新的一代,这一代的个体由于继承了上一代的一些优良性状,因而在性能上要优于上一代,这样逐步朝着最优解的方向进化.因此,遗传算法可以看成是一个由可行解组成的群体初步进化的过程.
算法/程序流程图
关键源代码
56. def Select_Crossover(chroms, fitness, prob=0.6): # 选择和交叉
57. probs = fitness/np.sum(fitness) # 各个个体被选择的概率
58. probs_cum = np.cumsum(probs) # 概率累加分布
59.
60. each_rand = np.random.uniform(size=len(fitness)) # 得到 10 个随机数 0 到 1 之间
62. # 轮盘赌,根据随机概率选择出新的基因编码
63. # 对于 each_rand 中的每个随机数,找到被轮盘赌中的那个染色体
64. newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
65. for rand in each_rand])
66.
67. # 繁殖,随机配对(概率为 0.6)
68.
69. # 这个数字小于 0.6 就交叉,则平均下来应有三组进行交叉,即 6 个染色体要进行交叉
70. pairs = np.random.permutation(
71. int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生 6 个随机数乱排一下分成二列
72. center = len(newX[0])//2 # 交叉方法采用最简单的,中心交叉法
73. for i, j in pairs:
74. # 在中间位置交叉
75. x, y = newX[i], newX[j]
76. newX[i] = x[:center] + y[center:] # newX 的元素都是字符串,直接用+号拼接
77. newX[j] = y[:center] + x[center:]
78. return newX
79.
80.
81. chroms = Select_Crossover(chroms, fitness)
82.
83. dechroms = decode(chroms)
84. fitness = fun(dechroms)
85.
86. for gene, dec, fit in zip(chroms, dechroms, fitness):
87. print("chrom=%s, dec=%5.2f, fit=%.2f" % (gene, dec, fit))
88.
89. # 对比一下选择和交叉之后的结果
90. fig, (axs1, axs2) = plt.subplots(1, 2, figsize=(14, 5))
91. axs1.plot(Xs, fun(Xs))
92. axs1.plot(population, fun(population), 'o')
93. axs2.plot(Xs, fun(Xs))
94. axs2.plot(dechroms, fitness, '*')
95. plt.show()
96.
97. # 输入一个原始种群 1,输出一个变异种群 2 函数参数中的冒号是参数的类型建议符。
98.
99.
100. def Mutate(chroms: np.array):
101. prob = 0.1 # 变异的概率
102. clen = len(chroms[0]) # chroms[0]="111101101 000010110" 字符串的长度=18
103. m = {'0': '1', '1': '0'} # m 是一个字典,包含两对:第一对 0 是 key 而 1 是 value;第二对 1
是 key 而 0 是 value
104. newchroms = [] # 存放变异后的新种群
105. each_prob = np.random.uniform(size=len(chroms)) # 随机 10 个数
106.
107. for i, chrom in enumerate(chroms): # enumerate 的作用是整一个 i 出来
108. if each_prob[i] < prob: # 如果要进行变异(i 的用处在这里)
109. pos = np.random.randint(clen) # 从 18 个位置随机找一个位置,假设是 7
110. # 0~6 保持不变,8~17 保持不变,仅将 7 号翻转,即 0 改为 1,1 改为 0。注意 chrom 中字符
不是 1 就是 0
111. chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
112. newchroms.append(chrom) # 无论 if 是否成立,都在 newchroms 中增加 chroms 的这个元素
113. return np.array(newchroms) # 返回变异后的种群
114.
115.
116. newchroms = Mutate(chroms)
122. dechroms = decode(chroms1)
123. fitness = fitfun(dechroms)
124. axs1.plot(Xs, fitfun(Xs))
125. axs1.plot(dechroms, fitness, 'o')
126.
127. dechroms = decode(chroms2)
128. fitness = fitfun(dechroms)
129. axs2.plot(Xs, fitfun(Xs))
130. axs2.plot(dechroms, fitness, '*')
131. plt.show()
132.
133.
134. # 对比一下变异前后的结果
135. DrawTwoChroms(chroms, newchroms, fun)
136.
137. # 上述代码只是执行了一轮,这里反复迭代
138. np.random.seed(0)
139. population = np.random.uniform(-1, 2, 100) # 这次多找一些点
140. chroms = encode(population)
141.
142. for i in range(1000):
143. fitness = fun(decode(chroms))
144. fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
145. newchroms = Mutate(Select_Crossover(chroms, fitness))
146. if i % 300 == 1:
147. DrawTwoChroms(chroms, newchroms, fun)
148. chroms = newchroms 149.
150. DrawTwoChroms(chroms, newchroms, fun)
实验结果与分析
-
代码第 64 行的语义是什么?两个[0]各自代表什么?最后 newX 有几个元素?
-
newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
-
for rand in each_rand])
① 第64行的代码是根据累积概率和轮盘赌的概率分布来选则要参与交叉的染色体;
② probs_cum = np.cumsum(probs) # 概率累加分布,计算出来的probs_cum是一个n行1列的二维数组每次取符合种群中的第一个数值。
Where产生的是一个二维数组[],第一个0是probs_cum中大于rand的数所组成的数组中的第一个,第二个0是取[]中第一个元素,取得的是probs_cum中第一个大于rand的元素。
③ newX 的元素是当前种群中的个体的个数,newX 的元素个数取决于当前种群。
-
代码第 70 行的语义是什么?为什么要除以 2 再乘以 2?reshape 中的-1 表示什么?
-
pairs = np.random.permutation(
-
int(len(newX)prob//22)).reshape(-1, 2) # 产生 6 个随机数乱排一下分成二列
①第70行代码是在种群总染色体数目为10的情况下根据交叉率为0.6选择6条染色体,两两随机配对进行交叉操作;
②要除以 2 再乘以 2是为了让pairs的个数为偶数,方面后面变形成两列的数组,Prob是各个个体被选择的概率
③-1表示对于行没有限制,根据总数据量和列数形成形状的二维数组。
3.请结合 Mutate 函数的内容,详述变异是如何实现的。
100. def Mutate(chroms: np.array):
101. prob = 0.1 # 变异的概率
102. clen = len(chroms[0]) # chroms[0]=“111101101 000010110” 字符串的长度=18
103. m = {‘0’: ‘1’, ‘1’: ‘0’} # m 是一个字典,包含两对:第一对 0 是 key 而 1 是 value;第二对 1
是 key 而 0 是 value
104. newchroms = [] # 存放变异后的新种群
105. each_prob = np.random.uniform(size=len(chroms)) # 随机 10 个数
106.
107. for i, chrom in enumerate(chroms): # enumerate 的作用是整一个 i 出来
108. if each_prob[i] < prob: # 如果要进行变异(i 的用处在这里)
109. pos = np.random.randint(clen) # 从 18 个位置随机找一个位置,假设是 7
110. # 0~6 保持不变,8~17 保持不变,仅将 7 号翻转,即 0 改为 1,1 改为 0。注意 chrom 中字符
不是 1 就是 0
111. chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
112. newchroms.append(chrom) # 无论 if 是否成立,都在 newchroms 中增加 chroms 的这个元素
113. return np.array(newchroms) # 返回变异后的种群
(1). 首先设置变异的概率
(2). 根据设置的变异概率,对初始种群中个体进行变异
(3). 随机选择n个元素,将这n个元素中的第j个元素取非
(4). 用变异后的元素替换原来的元素
4.将代码第 145 行修改为 newchroms = Select_Crossover(chroms, fitness),即不再执行变异, 执行结果有什么不同,为什么会出现这种变化?
进行一次Select_Crossover之后,选择的种群是比上一次合适的,下一代再次根据相同规则选的时候,第三代种群与第二代种群差别不大,所以,点都聚集在一个地方。只有每次Select_Crossover选择优势种群之后在进行Mutate变异才能逐渐向最优值逼近。
5.轮盘让个体按概率被选择,对于适应度最高的个体而言,虽然被选择的概率高,但仍有可能被淘汰,从而在进化过程中失去当前最优秀的个体。一种改进方案是,让适应度最高的那个个体不参与选择,而是直接进入下一轮(直接晋级),这种方案被称为精英选择(elitist selection)。请修改Select 部分的代码,实现这一思路。
56. def Select_Crossover(chroms, fitness, prob=0.6): # 选择和交叉
57. probs = fitness/np.sum(fitness) # 各个个体被选择的概率
58. probs_cum = np.cumsum(probs) # 概率累加分布
59.
60. prob_max_index = (np.where(probs == np.max(probs))[0][0]) #获取适应度最大的元素
60. new_chroms = np.delete(chroms,prob_max_index) #将适应度最大的元素暂时删除
probs = fitness/np.sum(fitness) # 更新各个个体被选择的概率
probs_cum = np.cumsum(probs) # 更新概率累加分布
60. each_rand = np.random.uniform(size=len(fitness)-1) # 得到 10 个随机数 0 到 1 之间
61.
62. # 轮盘赌,根据随机概率选择出新的基因编码
63. # 对于 each_rand 中的每个随机数,找到被轮盘赌中的那个染色体
64. newX = np.array([chroms[np.where(probs_cum > rand)[0][0]]
65. for rand in each_rand])
66. newX = np.append(newX,chroms[prob_max_index]) #最后把最大的元素添加到第二代种群中
67. # 繁殖,随机配对(概率为 0.6)
68.
69. # 这个数字小于 0.6 就交叉,则平均下来应有三组进行交叉,即 6 个染色体要进行交叉
70. pairs = np.random.permutation(
71. int(len(newX)*prob//2*2)).reshape(-1, 2) # 产生 6 个随机数乱排一下分成二列
72. center = len(newX[0])//2 # 交叉方法采用最简单的,中心交叉法
73. for i, j in pairs:
74. # 在中间位置交叉
75. x, y = newX[i], newX[j]
76. newX[i] = x[:center] + y[center:] # newX 的元素都是字符串,直接用+号拼接
77. newX[j] = y[:center] + x[center:]
78. return newX
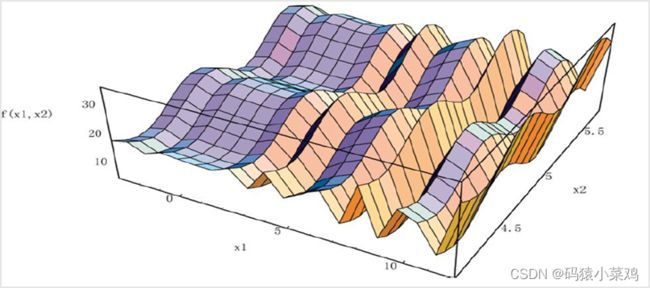
6.【选做】请借鉴示例代码,实现教材 P57 的例 2.6.1,即用遗传算法求解下列二元函数的最大值。
import numpy as np
import matplotlib.pyplot as plt
def fun1(x1,x2):
return 21.5 + x1*np.sin(4*np.pi*x1) + x2*np.sin(20*np.pi*x2)
X1 = np.linspace(-2.9, 12.0, 100)
X2 = np.linspace(4.2, 5.7, 100)
np.random.seed(0) # 令随机数种子=0,确保每次取得相同的随机数
# 初始化原始种群
#population = np.random.uniform(-1, 2, 10) # 在[-1,2)上以均匀分布生成10个浮点数,做为初始种群
population1 = np.random.uniform(-2.9, 12.0, 10) # 在[-1,2)上以均匀分布生成10个浮点数,做为初始种群
population2 = np.random.uniform(4.2, 5.7, 10) # 在[-1,2)上以均匀分布生成10个浮点数,做为初始种群
for pop1,pop2, fit in zip(population1,population2, fun1(population1,population2)):
print("x1=%5.2f, x2=%5.2f, fit=%.2f" % (pop1,pop2, fit))
#plt.plot(Xs, fun(Xs))
#plt.plot(population, fun(population), '*')
#plt.show()
def encode(population, _min=-1, _max=2, scale=2**18, binary_len=18): # population必须为float类型,否则精度不能保证
# 标准化,使所有数据位于0和1之间,乘以scale使得数据间距拉大以便用二进制表示
normalized_data = (population-_min) / (_max-_min) * scale
# 转成二进制编码
binary_data = np.array([np.binary_repr(x, width=binary_len)
for x in normalized_data.astype(int)])
return binary_data
chroms1 = encode(population1) # 染色体英文(chromosome)
chroms2 = encode(population2) # 染色体英文(chromosome)
print("chroms",chroms1)
print("chroms",chroms2)
#for pop, chrom, fit in zip(population1,population2, chroms1, chroms2, fun1(population1,population2)):
# print("x=%.2f, chrom=%s, fit=%.2f" % (pop, chrom, fit))
def decode(popular_gene, _min=-1, _max=2, scale=2**18): # 先把x从2进制转换为10进制,表示这是第几份
# 乘以每份长度(长度/份数),加上起点,最终将一个2进制数,转换为x轴坐标
return np.array([(int(x, base=2)/scale*3)+_min for x in popular_gene])
fitness = fun1(decode(chroms1),decode(chroms2))
#for pop, chrom, dechrom, fit in zip(population, chroms, decode(chroms), fitness):
# print("x=%5.2f, chrom=%s, dechrom=%.2f, fit=%.2f" %
# (pop, chrom, dechrom, fit))
fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
print(fitness)
def Select_Crossover(chroms1,chroms2, fitness, prob=0.6): # 选择和交叉
probs = fitness/np.sum(fitness) # 各个个体被选择的概率
probs_cum = np.cumsum(probs) # 概率累加分布
each_rand = np.random.uniform(size=(len(fitness))) # 得到9个随机数,0到1之间
# 轮盘赌,根据随机概率选择出新的基因编码
# 对于each_rand中的每个随机数,找到被轮盘赌中的那个染色体
newX1 = np.array([chroms1[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
newX2 = np.array([chroms2[np.where(probs_cum > rand)[0][0]] for rand in each_rand])
# 繁殖,随机配对(概率为0.6)
# 6这个数字怎么来的,根据遗传算法,假设有10个数,交叉概率为0.6,0和1一组,2和3一组。。。8和9一组,每组扔一个0到1之间的数字
# 这个数字小于0.6就交叉,则平均下来应有三组进行交叉,即6个染色体要进行交叉
pairs = np.random.permutation(int(len(newX1)*prob//2*2)).reshape(-1, 2) # 产生6个随机数,乱排一下,分成二列
center = len(newX1[0])//2 # 交叉方法采用最简单的,中心交叉法
for i, j in pairs:
# 在中间位置交叉
x, y = newX1[i], newX1[j]
newX1[i] = x[:center] + y[center:] # newX的元素都是字符串,可以直接用+号拼接
newX1[j] = y[:center] + x[center:]
for i, j in pairs:
# 在中间位置交叉
x, y = newX2[i], newX2[j]
newX2[i] = x[:center] + y[center:] # newX的元素都是字符串,可以直接用+号拼接
newX2[j] = y[:center] + x[center:]
return newX1,newX2
chroms1,chroms2 = Select_Crossover(chroms1,chroms2, fitness)
dechroms1 = decode(chroms1)
dechroms2 = decode(chroms2)
fitness = fun1(dechroms1,dechroms2)
# 输入一个原始种群1,输出一个变异种群2 函数参数中的冒号是参数的类型建议符,告诉程序员希望传入的实参的类型。函数后面跟着的箭头是函数返回值的类型建议符,用来说明该函数返回的值是什么类型。
def Mutate(chroms1: np.array):
prob = 0.1 # 变异的概率
clen = len(chroms1[0]) # chroms[0]="111101101 000010110" 字符串的长度=18
m = {'0': '1', '1': '0'} # m是一个字典,包含两对:第一对0是key而1是value;第二对1是key而0是value
newchroms = [] # 存放变异后的新种群
each_prob = np.random.uniform(size=len(chroms)) # 随机10个数
for i, chrom in enumerate(chroms): # enumerate的作用是整一个i出来
if each_prob[i] < prob: # 如果要进行变异(i的用处在这里)
pos = np.random.randint(clen) # 从18个位置随机中找一个位置,假设是7
# 0~6保持不变,8~17保持不变,仅将7号翻转,即0改为1,1改为0。注意chrom中字符不是1就是0
chrom = chrom[:pos] + m[chrom[pos]] + chrom[pos+1:]
newchroms.append(chrom) # 无论if是否成立,都在newchroms中增加chroms的这个元素
return np.array(newchroms) # 返回变异后的种群
newchroms1 = Mutate(chroms1)
newchroms2 = Mutate(chroms2)
# 对比一下变异前后的结果
#DrawTwoChroms(chroms, newchroms, fun)
# 上述代码只是执行了一轮,这里反复迭代
np.random.seed(0) #
population = np.random.uniform(-1, 2, 100) # 这次多找一些点
chroms = encode(population)
for i in range(1000):
fitness = fun1(decode(chroms1),decode(chroms2))
fitness = fitness - fitness.min() + 0.000001 # 保证所有的都为正
#newchroms = Select_Crossover(chroms, fitness)
newchroms1,newchroms2 = Mutate(Select_Crossover(chroms, fitness))
chroms1,chroms2 = newchroms1,newchroms2