数据挖掘——AdaBoost(波士顿房价预测)
#回归:
#用 AdaBoost 回归分析对波士顿房价进行了预测
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_boston
from sklearn.ensemble import AdaBoostRegressor
# 加载数据
data=load_boston()
# 分割数据
train_x, test_x, train_y, test_y = train_test_split(data.data, data.target, test_size=0.25, random_state=33)
# 使用AdaBoost回归模型
regressor=AdaBoostRegressor()
regressor.fit(train_x,train_y)
pred_y = regressor.predict(test_x)
mse = mean_squared_error(test_y, pred_y)
print("房价预测结果 ", pred_y)
print("均方误差 = ",round(mse,2))
#用不同的回归分析模型分析这个数据集,比如使用决策树回归和 KNN 回归。
#相比之下,AdaBoost 的均方误差更小,也就是结果更优
# 使用决策树回归模型
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
from sklearn.neighbors import KNeighborsRegressor
dec_regressor=DecisionTreeRegressor()
dec_regressor.fit(train_x,train_y)
pred_y = dec_regressor.predict(test_x)
mse = mean_squared_error(test_y, pred_y)
print("决策树均方误差 = ",round(mse,2))
# 使用KNN回归模型
knn_regressor=KNeighborsRegressor()
knn_regressor.fit(train_x,train_y)
pred_y = knn_regressor.predict(test_x)
mse = mean_squared_error(test_y, pred_y)
print("KNN均方误差 = ",round(mse,2))
输出:
房价预测结果 [19.46829268 10.36153846 12.40547945 17.61021505 24.25621302 21.64597701
27.84137931 18.29361702 31.41977401 19.52178218 27.97631579 31.71045752
11.93846154 24.25621302 14.40512821 24.42258065 18.29361702 16.83405405
27.84137931 24.25621302 17.61021505 17.61021505 17.61021505 19.46829268
30.83291139 17.93913043 20.29881423 24.42258065 11.93846154 30.83291139
17.41129032 25.26237624 11.93846154 20.04871795 27.07255814 31.41977401
24.54736842 11.93846154 14.56 24.42258065 15.66527778 11.93846154
29.48863636 17.53058824 27.0745098 19.2975 18.29361702 19.52178218
26.00732984 19.35681818 17.61021505 32.90392157 16.61101695 17.16122449
24.54736842 20.04871795 24.42258065 16.94255319 24.46016949 21.74742268
19.52178218 16.28970588 44.60454545 21.60949367 17.16122449 26.00732984
24.54736842 11.93846154 18.91612903 27.84137931 23.36478261 18.92142857
18.29361702 27.27124464 19.35681818 45.87954545 15.66527778 11.93846154
17.61021505 24.41785714 19.92431193 15.8 12.20727273 24.54736842
20.29881423 20.29881423 47.71875 17.16122449 44.305 32.07476636
30.16 19.52178218 19.02453704 17.41129032 13.91818182 33.71904762
24.25621302 23.36478261 18.92142857 18.92142857 16.40803571 19.78731343
27.46791045 24.54736842 11.93846154 16.61101695 11.97051282 27.0745098
11.38974359 25.26237624 50. 12.40547945 17.61021505 24.46016949
31.41977401 24.41785714 21.60949367 20.04871795 27.0745098 19.99555556
19.78731343 18.91612903 11.97051282 20.04871795 20.29881423 17.61021505
42.84 ]
均方误差 = 17.37
决策树均方误差 = 25.06
KNN均方误差 = 27.87
分类问题:
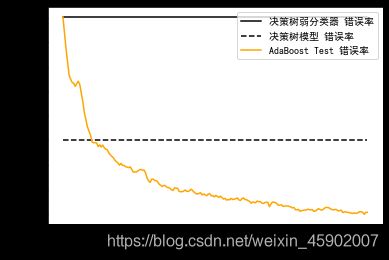
#用三种模型分别进行训练,然后用测试集进行预测,并将三个分类器的错误率进行可视化对比,可以看到这三者之间的区别:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.metrics import zero_one_loss
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
# 设置AdaBoost迭代次数
n_estimators=200
# 使用
X,y=datasets.make_hastie_10_2(n_samples=12000,random_state=1)
# 从12000个数据中取前2000行作为测试集,其余作为训练集
train_x, train_y = X[2000:],y[2000:]
test_x, test_y = X[:2000],y[:2000]
# 弱分类器
dt_stump = DecisionTreeClassifier(max_depth=1,min_samples_leaf=1)
dt_stump.fit(train_x, train_y)
dt_stump_err = 1.0-dt_stump.score(test_x, test_y)
# 决策树分类器
dt = DecisionTreeClassifier()
dt.fit(train_x, train_y)
dt_err = 1.0-dt.score(test_x, test_y)
# AdaBoost分类器
ada = AdaBoostClassifier(base_estimator=dt_stump,n_estimators=n_estimators)
ada.fit(train_x, train_y)
# 三个分类器的错误率可视化
fig = plt.figure()
# 设置plt正确显示中文
plt.rcParams['font.sans-serif'] = ['SimHei']
ax = fig.add_subplot(111)
ax.plot([1,n_estimators],[dt_stump_err]*2, 'k-', label=u'决策树弱分类器 错误率')
ax.plot([1,n_estimators],[dt_err]*2,'k--', label=u'决策树模型 错误率')
ada_err = np.zeros((n_estimators,))
# 遍历每次迭代的结果 i为迭代次数, pred_y为预测结果
for i,pred_y in enumerate(ada.staged_predict(test_x)):
# 统计错误率
ada_err[i]=zero_one_loss(pred_y, test_y)
# 绘制每次迭代的AdaBoost错误率
ax.plot(np.arange(n_estimators)+1, ada_err, label='AdaBoost Test 错误率', color='orange')
ax.set_xlabel('迭代次数')
ax.set_ylabel('错误率')
leg=ax.legend(loc='upper right',fancybox=True)
plt.show()