Open3d之表面重建
在许多场景下我们希望生成密集的3D几何形状,比如三角网格。然而从多视图立体算法和深度传感器中我们只能够获得非结构化的点云数据。我们需要使用表面重建算法来从非结构化的输入中得到三角网格。Open3d实现了文献中已有的算法:
- Alpha shapes [Edelsbrunner1983]
- Ball pivoting [Bernardini1999]
- Poisson [Kazhdan2006]
Alpha shapes
alpha shape [Edelsbrunner1983]是凸包的概括。如这里所介绍的,可以直观地将Alpha shapes理解为以下内容:想象有一个包含有巧克力硬块的巨大冰淇凌,巧克力硬块是点![]() 。用一种球形的冰淇淋勺,可以在不碰到巧克力块的情况下挖出冰淇淋的所有部分,甚至可以在内部挖出一些孔(比如一些在外部移动勺子无法触及的部分。)我们最终得到一个以帽盖,弧线和点为边界的对象(不一定是凸的)。如果我们将所有的圆面都拉成三角形和线段,则可以直观的描述点
。用一种球形的冰淇淋勺,可以在不碰到巧克力块的情况下挖出冰淇淋的所有部分,甚至可以在内部挖出一些孔(比如一些在外部移动勺子无法触及的部分。)我们最终得到一个以帽盖,弧线和点为边界的对象(不一定是凸的)。如果我们将所有的圆面都拉成三角形和线段,则可以直观的描述点![]() 的alpha shape。
的alpha shape。
Open3d实现了该算法,接口为create_from_point_cloud_alpha_shape其中包含了一个权重参数 alpha。
# -*- coding: UTF-8 -*-
import numpy as np
import open3d as o3d
import Open3D.examples.python.open3d_tutorial as o3dtut
# 加载网格
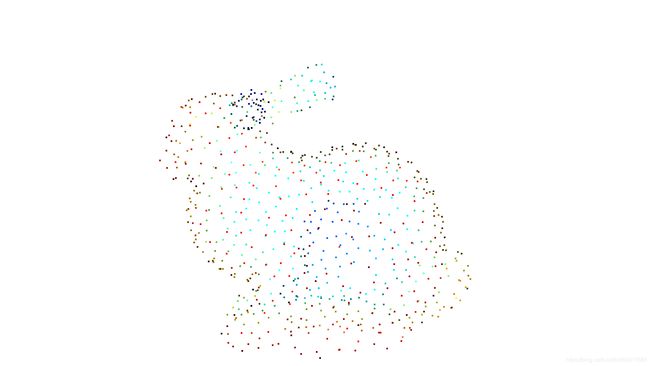
mesh = o3dtut.get_bunny_mesh()
# 网格点采样
pcd = mesh.sample_points_poisson_disk(750)
# 可视化
o3d.visualization.draw_geometries([pcd])
# 重建
alpha = 0.03
print(f"alpha={alpha:.3f}")
mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_alpha_shape(pcd, alpha)
# 计算定点法线
mesh.compute_vertex_normals()
# 可视化
o3d.visualization.draw_geometries([mesh], mesh_show_back_face=True)alpha-0.030

这个算法是基于点云的凸包算法实现的。如果我们想从给定的点云中计算多个alpha shapes,我们只需要计算一次凸包并将其传递给create_from_point_cloud_alpha_shape,这样可以节省一些计算。
tetra_mesh, pt_map = o3d.geometry.TetraMesh.create_from_point_cloud(pcd)
for alpha in np.logspace(np.log10(0.5), np.log10(0.01), num=4):
print(f"alpha={alpha:.3f}")
mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_alpha_shape(
pcd, alpha, tetra_mesh, pt_map)
mesh.compute_vertex_normals()
o3d.visualization.draw_geometries([mesh], mesh_show_back_face=True)alpha=0.500
alpha=0.136
alpha=0.037
alpha=0.010
滚球法
与alpha shape相关的一种表面重建算法是滚球法(ball pivoting algorithm,BPA)。直观的讲,我们想象有一个给定半径的3D球,将其放到点云数据上。如果这个球碰到了三个点(并且不会在回到这三个点),那我们就创造一个三角形。之后呢,我们的球开始沿着已有三角形的边开始滚动,每次碰到不重复的三个点时就会创造一个三角形。
Open3d在接口create_from_point_cloud_ball_pivoting中实现了该算法。这个算法有一个接受的列表参数radii,这个列表会创建若干个不同半径的独立的球,之后开始在点云上滚动。
注意:这个算法需要点云包含法线参数。
gt_mesh = o3dtut.get_bunny_mesh()
gt_mesh.compute_vertex_normals()
pcd = gt_mesh.sample_points_poisson_disk(3000)
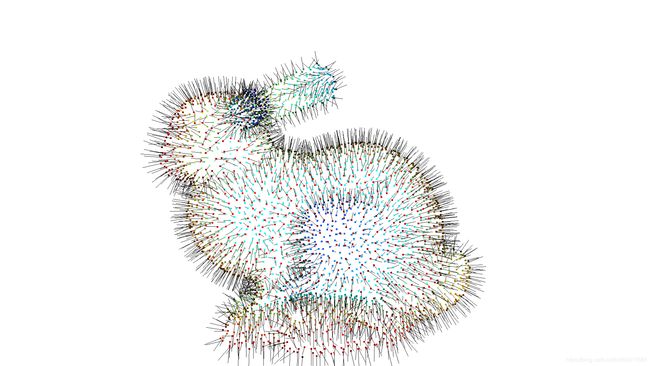
o3d.visualization.draw_geometries([pcd], point_show_normal=True)
radii = [0.005, 0.01, 0.02, 0.04]
rec_mesh = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
pcd, o3d.utility.DoubleVector(radii))
o3d.visualization.draw_geometries([pcd, rec_mesh])
泊松表面重建
表面重建算法会产生不平滑的结果,这是因为点云的点也是三件网格的顶点。无需进行任何修改。泊松表面重建算法 [Kazhdan2006]解决了正规优化的问题,这样就可以产生光滑的表面。
Open3d实现了算法接口create_from_point_cloud_poisson,该接口基本上是Kazhdan实现的代码接口的封装。这个接口有一个重要的参数就是depth,depth定义了用于重建的八叉树的深度。较高的depth值意味着网格有着较高的细节。
Note:
这个算法要求点云包含法线信息。
pcd = o3dtut.get_eagle_pcd()
print(pcd)
o3d.visualization.draw_geometries([pcd], zoom=0.664,
front=[-0.4761, -0.4698, -0.7434],
lookat=[1.8900, 3.2596, 0.9284],
up=[0.2304, -0.8825, 0.4101])
print('run Poisson surface reconstruction')
with o3d.utility.VerbosityContextManager(o3d.utility.VerbosityLevel.Debug) as cm:
mesh, densities = o3d.geometry.TriangleMesh.create_from_point_cloud_poisson(pcd, depth=9)
print(mesh)
o3d.visualization.draw_geometries([mesh], zoom=0.664,
front=[-0.4761, -0.4698, -0.7434],
lookat=[1.8900, 3.2596, 0.9284],
up=[0.2304, -0.8825, 0.4101])
downloading eagle pcl
geometry::PointCloud with 796825 points.
run Poisson surface reconstruction
geometry::TriangleMesh with 563112 points and 1126072 triangles.

泊松表面重建还将在低密度的点云中创建三角形,甚至可以推断出一些区域(比如上面输出的底座的边缘)。函数create_from_point_cloud_poisson还有第二个返回的值densities来表示每个顶点的密度。低密度值意味着这个顶点只从输入的点云中收到少量点的支持。
下面的代码我们通过伪彩可视化了3D形状的密度。紫色表明低密度,黄色表明高密度。
print('visualize densities')
densities = np.asarray(densities)
density_colors = plt.get_cmap('plasma')(
(densities - densities.min()) / (densities.max() - densities.min()))
density_colors = density_colors[:, :3]
density_mesh = o3d.geometry.TriangleMesh()
density_mesh.vertices = mesh.vertices
density_mesh.triangles = mesh.triangles
density_mesh.triangle_normals = mesh.triangle_normals
density_mesh.vertex_colors = o3d.utility.Vector3dVector(density_colors)
o3d.visualization.draw_geometries([density_mesh], zoom=0.664,
front=[-0.4761, -0.4698, -0.7434],
lookat=[1.8900, 3.2596, 0.9284],
up=[0.2304, -0.8825, 0.4101])
visualize densities

我们可以通过密度值来筛选掉那些具有比较低的支持率的顶点和三角形。
下面的代码中我们移除了所有密度值低于0.01 0.010.01的顶点和它所连接的三角形。
print('remove low density vertices')
vertices_to_remove = densities < np.quantile(densities, 0.01)
mesh.remove_vertices_by_mask(vertices_to_remove)
print(mesh)
o3d.visualization.draw_geometries([mesh], zoom=0.664,
front=[-0.4761, -0.4698, -0.7434],
lookat=[1.8900, 3.2596, 0.9284],
up=[0.2304, -0.8825, 0.4101])
remove low density vertices
geometry::TriangleMesh with 557480 points and 1113214 triangles.
法线估计
在上面的示例中,我们假设点云的法线朝外。但是,并非所有的点云都已经具有关联的法线。Open3D可用于使用带有Estimate_Normals的点云法线来估计点云法线,该局部法线适合每个3D点的平面以导出法线。但是,估计的法线可能未始终一致。 orient_normals_consistent_tangent_plane使用最小生成树传播法线方向。
gt_mesh = o3dtut.get_bunny_mesh()
pcd = gt_mesh.sample_points_poisson_disk(5000)
pcd.normals = o3d.utility.Vector3dVector(np.zeros(
(1, 3))) # invalidate existing normals
pcd.estimate_normals()
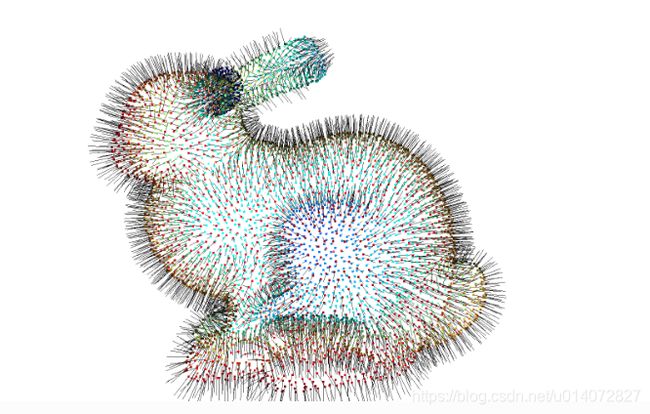
o3d.visualization.draw_geometries([pcd], point_show_normal=True)
pcd.orient_normals_consistent_tangent_plane(100)
o3d.visualization.draw_geometries([pcd], point_show_normal=True)