欧氏距离_机器学习中的分类距离
作者 | 我的智慧生活
来源 | 咪付
生活中,距离通常是用于形容两个地方或两个物体之间的远近。在人工智能机器学习领域,常使用距离来衡量两个样本之间的相似度。
“物以类聚”
我们知道“物以类聚”通常用于比喻同类的东西经常聚在一起。机器学习中,距离就是遵循物以类聚的思想。通过两个样本特征数据进行距离计算后,得到的距离值越小,代表两者的相似度越高,属于同一类的可能性就越高。换句话说,距离能够决定样本的归属。
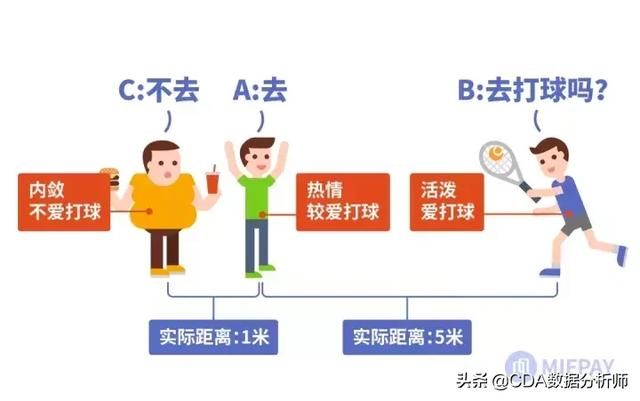
例如,在下图中,对于机器学习来说存在着两种距离:
(1)一是人物的空间位置距离;
(2)二是人物的性格爱好距离。
对第1种距离来说,A与C较A与B近;而对第2种距离来说,则是A与B较近(爱打球)。A与B的爱好距离可通过如下计算:
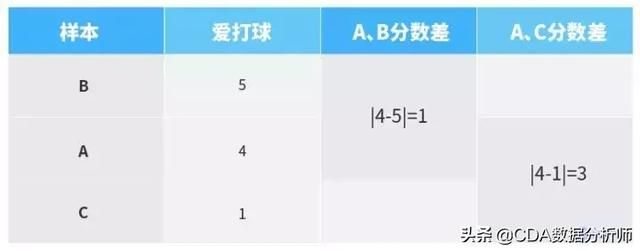
我们用0—10分来表征每个人对打球的喜好程度,分数越高代表越爱打球,假设A、B、C三人的分值分别如下:
可以看出,A、B两人的分数较接近,A、B两人的分数差小于A、C两人的分数差,这个分数差值也就是机器学习中要计算的距离。通过比较得出,A、B两者的距离小,容易归为一类。当然,这里仅仅分析了爱打球这一个特征属性,机器学习中通常涉及多个属性进行综合计算和判断,也就是多维度分析。
物理几何空间距离
机器学习中,计算两个样本点之间的距离有多种不同的距离衡量方法,其中最常见的就是采用物理几何空间距离进行衡量。所谓物理几何空间距离就是点到点之间在物理空间中的真实距离。通俗地说,这类距离看得见、摸得着。常见的物理几何空间距离有:
欧氏距离
(Euclidean Distance)
曼哈顿距离
(Manhattan Distance)
切比雪夫距离
(Chebyshev Distance)
闵氏距离
(Minkowski Distance)
夹角余弦
(Cosine)
这几类物理几何空间距离的应用非常多,尤其是欧氏距离。
曼哈顿距离
我们首先从曼哈顿距离来形象了解机器学习中的距离,曼哈顿距离也是机器学习中常采用的一种距离。
我们知道曼哈顿是“世界的十字路口”,那里有非常多的十字交叉路口。
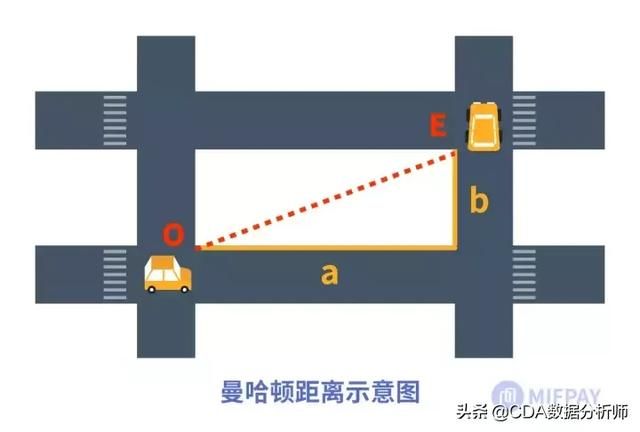
曼哈顿距离,说的是从街区中的一个十字路口到另一个十字路口所经过的街区距离,因此也称为城市街区距离。下图中给出了曼哈顿距离的形象说明,当我们开车从街区的一个十字路口(O)到了另一个十字路口(E)所经过的街区距离为:a+b,这就是曼哈顿距离。
O、E两点之间直线段距离是我们生活中常说的两个地方(O、E)之间的距离,而在实际街区中的情形,车辆无法从O沿直线开到E,除非具备像蜘蛛侠一样的飞行本领可以穿越其中的大楼,这就是曼哈顿距离的由来。
一图看清“欧曼雪”
下面我们再从简单的二维平面坐标图来对比了解欧氏距离、曼哈顿距离和切比雪夫距离(以下简称“欧曼雪”)这三种距离的区别。
上图是由X和Y组成的二维平面坐标,现有A、B两个二维样本值,其投影坐标点分别为:
A(X1,Y1)、B(X2,Y2)
A、B两点之间的直线段距离(图中的c)就是A、B两个样本的欧氏距离。因此,欧氏距离就是两个样本值投影在其坐标空间上的两点之间的直线距离。
如何计算A与B之间的欧氏距离?
从图中可以看出,A、B两点之间的直线段(c)与其横坐标差值线段:
a=X2-X1
纵坐标差值线段:
b=Y2-Y1
构成了一个直角三角形,根据勾股定理的关系可知:
c²=a²+b²
因此,我们可以根据坐标点A(X1,Y1)、B(X2,Y2),求得c值。即计算式为:
c²=a²+b²=(X2-X1)²+(Y2-Y1)²
A与B之间的曼哈顿距离又是怎样的距离呢?
上图中曼哈顿距离是由A沿直线走到C,再由C沿直线走到B,总共经过的距离,即为:
a+b=|X1-X2|+|Y1-Y2|
再来看切比雪夫距离,在上述二维平面坐标示意图中,A与B之间的切比雪夫距离则是选取a、b中值最大的,若a>b,切比雪夫距离即等于a,其计算表达式为:
Max(|X1-X2|,|Y1-Y2|)
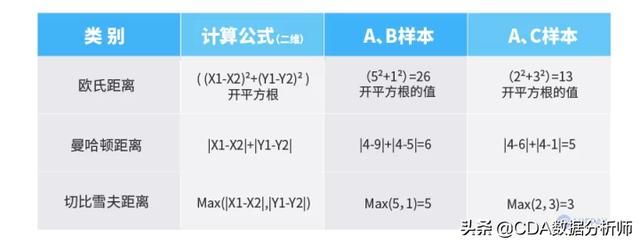
由此可看出,上述“欧曼雪”三种距离的实质分别如下:
- 欧氏距离 -
两个样本同一特征分量值差值的平方之和,再开平方根
- 曼哈顿距离 -
两个样本同一特征分量值差值的绝对值之和
- 切比雪夫距离 -
两个样本同一特征分量值差值的绝对值中的最大值
假如现在有三个人A、B和C(即样本A、样本B和样本C),我们需要以性格、爱好这两个属性为依据来判断他们的相似度,A、B、C的综合属性值则表示为:A(性格1,爱好1)、B(性格2,爱好2)、C(性格3,爱好3)。
我们设定上述性格、爱好等每个分量特征属性的取值范围为0—10分。以性格活泼、爱好打球具体属性为例,若性格很活泼,分值为10,若性格不活泼,分值则为0分,其余介于很活泼和不活泼之间的,则取0—10之间的分值;同理,若很爱打球,分值为10分,不爱打球,分值则为0分,其余介于很爱打球和不爱打球之间的,则取0—10之间的分值。
针对性格活泼、爱好打球的两项特征,假设A、B、C三人的取值分别如下:
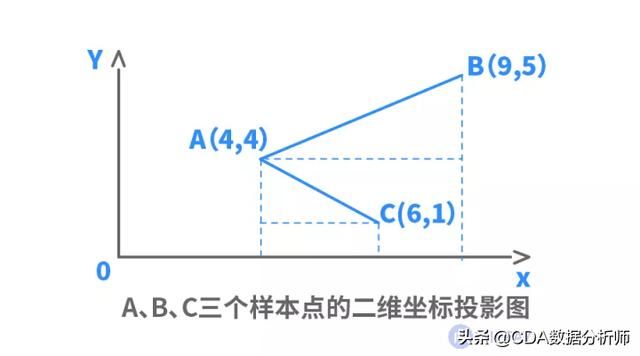
我们现以上述A、B、C三个样本A(4,4)、B(9,5)、C(6,1)投影到二维坐标上,分别计算A、B样本之间和A、C样本之间各自的欧氏距离、曼哈顿距离和切比雪夫距离,参照二维坐标投影图,计算结果如下:
从上表结果可知,A、C两个样本的欧氏距离、曼哈顿距离和切比雪夫距离均小于A、B两个样本,因此,A与C的相似度较高。这一结果与二维坐标图上的直观显示相符(即线段AC
闵氏距离
由上述例子的计算结果可知,尽管欧氏距离、曼哈顿距离和切比雪夫距离各自的定义和计算都不相同,但它们最终衡量的结果是相一致的。这三类距离也可归为闵氏距离。
闵氏距离也称闵可夫斯基距离,根据其变参数p的不同,可以归为不同类型的距离,比如:曼哈顿距离(p=1);欧氏距离(p=2);切比雪夫距离(p→∞)。
我们已经知道欧氏距离的实质是两个样本同一特征分量值差值的平方和,然后再开平方根,这里的平方指数就是闵氏距离的变参数p取2,如果平方指数(即2次方)换成其他次方(比如1,3,4次方等等),那就是其他类闵氏距离。
因此,也可以将闵氏距离看成是欧氏距离指数的推广距离,两者实质特点对比如下:
可见,闵氏距离不仅涵盖了“欧曼雪”三种距离,实则也是欧氏距离指数的推广(指数范围扩大到任意整数)距离。
当然,以上仅考虑了性格、爱好这两个特征属性来分析判断两个人的相似度。但是如果仅凭性格、爱好两个方面来预估两人的相似度,似乎有点过于简单粗暴,通常情况下,我们还要结合更多的特征因素来综合考虑,例如人生观、价值观、家庭背景等,从而得出更加准确的归类判断结果。如果在性格、爱好两个特征的基础上增加人生观这一特征因素来评判,A、B两人的综合属性值则表示为:A(性格1,爱好1,人生观1)、B(性格2,爱好2,人生观2),其具体特征值假设为:A(4,4,3)、B(9,5,6),在计算各类距离时,则相应增加人生观这一特征的差值。例如:
曼哈顿距离计算为:
|4-9|+|4-5|+|3-6|=9;
切比雪夫距离计算为:
Max(|4-9|,|4-5|,|3-6|)=Max(5,1,3)=5;
欧氏距离计算为:
(4-9)²+(4-5)²+(3-6)² =5²+1²+3²=35,再开平方根所得。
对比上表中两维的计算式,可见,增加了|3-6|或(3-6)²这一项差值。
同理,如果在性格、爱好、人生观这三个特征属性的基础上,还需考虑价值观、家庭背景这两个特征属性,总共就变成了五个分量特征,那就是五维的情形。在计算上述各类距离时,则相应增加价值观、家庭背景这两个分量特征的差值。
可见,每增加一个分量特征,维度就增加一个,计算距离时则相应增加该维度分量特征的差值。人工智能机器学习中,为了达到更准确的分类目的,往往要涉及非常多的维度,因而其计算量也相应增大。例如我们熟悉的人脸识别应用中通常采用512维特征向量,即有512个分量特征,以更好地区别出每一个人。
假设分别用两个特征向量:
A(X1, X2,....,X511, X512)
B(Y1, Y2,....,Y511, Y512)
来表示两个512维人脸特征数据,则该两个人脸样本之间的欧氏距离为:
( (Y1-X1) ²+(Y2-X2) ² +......+(Y511-X511) ² +(Y512-X512) ²)
计算求得512个分量值差的平方和,再开平方根,即为两者的欧氏距离。这就是高维欧氏距离的计算。
夹角余弦
除了以上各类常见的闵氏距离,还有一种较常用的距离,那就是夹角余弦。夹角余弦根据两个样本向量的夹角余弦值大小来确定样本的相似性。余弦值越接近1,余弦夹角就越接近0度,两个向量越相似。
现我们仍以简单的平面二维坐标的来了解夹角余弦的本质。以上述A、B、C三个样本A(4,4)、B(9,5)、C(6,1)为例,其在二维平面坐标的投影点如下图所示,从坐标原点O出发分别指向A、B、C三个点的线段(OA、OB、OC)则为A、B、C三个样本点的向量,A、B之间的向量夹角则为θ1,A、C之间的向量夹角则为θ2,根据三角形AOB的边长可计算出θ1的余弦值,根据三角形AOC的边长可计算出θ2的余弦值。θ1、θ2夹角示意图及其计算式如下表所示:
夹角余弦计算公式(二维)
根据两个样本的坐标值计算
余弦值取值范围为[-1,1]。余弦值越大,夹角越小。
A、B样本夹角余弦值
向量OA与OB之间的夹角余弦值
A、C样本夹角余弦值
向量OA与OC之间的夹角余弦值
可以得出θ1
通过对比发现,以上夹角余弦相似度的判断结果与欧氏距离等的判断结果正好相反。这是为什么呢?这是因为欧氏距离和余弦相似度各自的计算方式和衡量角度不相同,欧氏距离关注的是两点之间的绝对距离,而夹角余弦相似度注重的是两个向量在方向上的差异,而非距离。如下二维坐标图中,有A、C两个样本,欧氏距离关注的是AC两点的直线段距离,与OA、OC线段长度密切相关;而夹角余弦则是关注OA线段与OC线段重合需扫过的角度(θ)大小,与OA、OC线段长度无关。因此,夹角余弦相似度是整体方向性上的判断,而欧氏距离则是各分量特征的绝对差值判断。
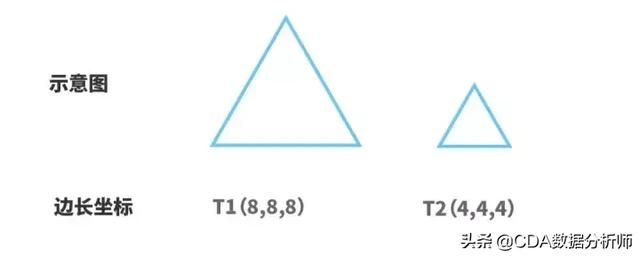
我们还可以用两个等边三角形的例子来具体了解两者的实质差别。假设有两个等边三角形T1和T2,其边长分别为8和4,现以三个边长为分量特征属性来表征三角形,其在三维空间的投影坐标点分别为T1(8, 8, 8)、T2(4, 4, 4)。由边长数值可知,两个等边三角形虽然边长差距大,但形状完全相似。从其投影坐标点可知,由于T1、T2各个边长分量差值相同,两个坐标点在三维空间坐标上投影方向完全相同。对T1、T2之间的欧氏距离及夹角余弦作对比如下:
从以上对比分析可以看出,欧氏距离和余弦相似度各自的评判标准不同,得出的结论也可能完全不同,因此,两者可根据适用的场合选择采用。欧氏距离适用于需要从每个分量特征差距中体现差异的分析,如通过用户行为指标分析用户价值相似度。余弦相似度更适用于综合性的导向评价,如通过用户对内容评分来区分用户兴趣的相似度等,余弦相似度也常用于计算两个文本之间的相似度。
以上各类常见的物理几何空间距离不仅容易理解,而且方便好用,在样本各个维度数据完整好的情况下具有较理想的预判效果。但同时这几类距离也存在着一些明显的不足,如缺乏考虑各分量之间的相关性影响、各分量特征侧重排序等。
例如上述的例子中,也许需要对性格、爱好、人生观、价值观、家庭背景等分量特征进行侧重排序,又或者人生观这一分量特征会对价值观、爱好等分量特征有影响。如需考虑分量相关性、个体相对于总体的比重等相关因素,更多则是采用基于概率统计的分布距离,较常用的有:马氏距离、巴氏距离、杰卡德相似系数、皮尔逊系数等。这些距离的计算多涉及统计学及概率论知识,因而相对较复杂。
但无论是物理几何空间距离,还是基于概率统计的分布距离,它们的中心思想都是统一的,那就是距离越近越相似。
扫码进入CDA官方小程序,解锁更多新鲜资讯和优质内容,还有免费试听课程,不要错过哟!