无人机高度估计_卡尔曼滤波
一、 卡尔曼滤波公式
-
线性系统的离散状态空间表达式:这是卡尔曼五个标准公式的基础
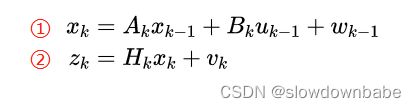
①式叫做系统状态方程:
xk: k时刻系统状态变量值
Ak:状态转移矩阵
Bk: 控制矩阵
uk-1: k-1时刻系统的输入
wk-1: k-1时刻的过程噪声,服从高斯分布,均值为0,协方差为Q
②式叫做观测方程:与传感器测量值有关
zk: k时刻的观测值/测量值;
Hk: 观测矩阵
vk: k时刻的测量噪声,服从高斯分布,均值为0,协方差为R -
卡尔曼滤波的五个标准公式:分为时间更新方程和测量更新方程
2.1 时间更新方程(2个方程)
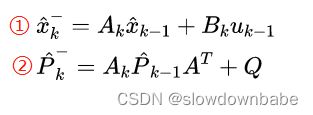
①式等式左边的符号表示 xk的先验估计,即xk的估计值的预测值
②式等式坐标的符号表示误差协方差矩阵的先验估计,Q表示过程噪声协方差矩阵
2.2 测量更新方程(3个方程)
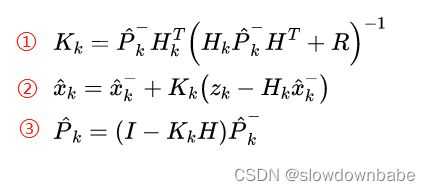
①式:Kk表示卡尔曼增益。Kk趋近0时,②式的结果更相信估计值;Kk趋近1时,更相信测量值。实际调参过程中调的是Q(过程噪声协方差矩阵)和R(测量噪声协方差矩阵),然后Q,R 值影响了Kk。Q越大,表示越不相信估计值,R越大表示越不相信测量值。
②式:状态的后验估计。这就是卡尔曼滤波的最终的结果。里面包含和估计值的预测值和观测值。
③式:误差协方差矩阵的后验估计。
二、 利用卡尔曼滤波估计高
这里使用的气压计(SPL06)和加速度计(MPU9250)进行融合。这里忽略了噪声。
步骤1:明确几个变量
系统的输入变量uk : 地球系下的加速度。
系统状态变量(2个)Xk: Pk,表示位置,这里指的是高度;Vk,表示速度变量;更明确的来说是地球系下Z轴的位移和Z轴的速度。
系统观测变量: Zk,表示气压计测量到的高度。这里要转换到地球系。
步骤2:确定系统的离散状态空间表达式,然后根据表达式写出矩阵方程,最后就得到了A,H,B
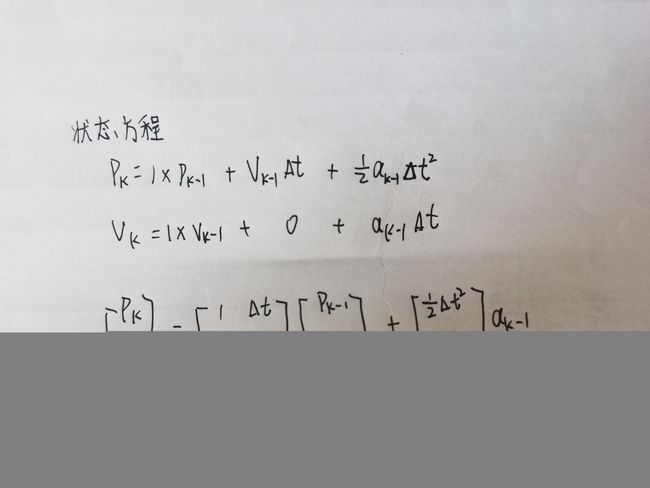
三、 实战:移植到MiniFly微型四轴上面
MiniFly是正点原子的开源微型四轴,使用的是stm32F4系列MCU,上面搭载了气压计,可以进行定高。
MiniFly高度估计代码的位置:
Firmware_F411 V1.4(改灯)\FLIGHT\src\state_estimator.c

传入的参数是Z轴加速度和气压计高度(如果接上了光流模块,使用的是光流模块上面的测距仪测到的高度)。因此我们可以使用自己些的kalman滤波高度估计算法,替代原来代码的实现。

四、卡尔曼滤波的调参
kalman调的参数只有两个Q和R。增大Q表示越不信任估计量,增大R表示越不信任观测量。在卡尔曼滤波高度估计中,设置R=1,Q=4e-8f,效果较好。
五、卡尔曼滤波实现高度估计的代码
代码中的矩阵运算使用的是STM32提供的DSP_LIB
/*
dt:传递给A和B的时间
acc: kalman滤波的输入1
atti: kalman滤波的输入2
Q: 根据经验给定过程噪声协方差矩阵,这里是一个2X2矩阵
R: 根据经验给定测量噪声协方差矩阵
pos_esti: kalman滤波结果输出1
vel_esti: kalman滤波结果输出2
*/
void KalmanPosZEsti(float dt, // 时间间隔
float accz, // 地球系下,Z轴加速度 (m/s^2)
float atti, // 地球系下,气压计(或测距仪)测量的高度 (m)
const float R,
const float Q,
float *pos_esti, // 位置估计
float *vel_esti)
{
/*定义保存矩阵A,B值的一维数组*/
static float A[4] = { 0 }; //一维数组
static float B[2] = { 0 };
static float H[2] = { 0 };
static float HPHT[1] = {0} ; // 特例
static float HT[2] = { 0 };
static float Q_[4] = {0};
static float X_[2] = {0,0}; // 状态变量的先验估计初始值为{0,0}
static float X[2] = {0.0f,0.0f}; // 状态变量的后验估计初始值为{0,0}
static float P_[4] = {0,0,0,0}; // 误差协方差矩阵先验的初始值为{0,0,0,0}
static float P[4] = {1.0,0,0,1.0}; // 误差协方差矩阵后验的初始值为{1,0,0,1}
static float AX[2] = {0,0};
static float AHATP[4] = {0};
static float AHATPAT[4] = {0};
static float PHT[2] = { 0 };
static float KH[4] = {0};
static float32_t K[2] = {0};
static float HK[2] = { 0 };
static float I_KH[2] = { 0 };
static float I[4] = {1,0,0,1};
static float u = 0; // 定义控制变量,也就是系统的输入
// 定义矩阵实例
arm_matrix_instance_f32 _A; // 定义一个矩阵实例 _A,保存一维数组A的值
arm_matrix_instance_f32 _A_T; // 定义一个矩阵实例 _A_T ,保存一维数组A的值
arm_matrix_instance_f32 _B; // 定义一个矩阵实例 _B,保存一维数组B的值
arm_matrix_instance_f32 _H; // 定义一个矩阵实例 _H,保存一维数组H的值
arm_matrix_instance_f32 _HT; // 定义一个矩阵实例 _HT,保存一维数组H的值
arm_matrix_instance_f32 hatx_; // Xk的先验估计
arm_matrix_instance_f32 hatx; // Xk的后验估计
arm_matrix_instance_f32 hatP_; // P的先验估计 hatP_
arm_matrix_instance_f32 hatP; // P的后验估计 hatP
arm_matrix_instance_f32 Kk; // kalman增益
arm_matrix_instance_f32 _KH;
arm_matrix_instance_f32 _I_KH;
arm_matrix_instance_f32 _I;
// 临时的中间矩阵
arm_matrix_instance_f32 A_hatX; // Ak * hatXk-1
arm_matrix_instance_f32 A_hatP; // Ak * hatPk-1
arm_matrix_instance_f32 A_hatPAT; // Ak * hatPk-1 * AT
arm_matrix_instance_f32 HkhatPk_;
arm_matrix_instance_f32 hatPk_HkT; // hatPk_ * HkT
arm_matrix_instance_f32 HP_HT; //H*P_*H'
arm_matrix_instance_f32 _Q;
Q_[0] = Q;
Q_[1] = 0;
Q_[2] = 0;
Q_[3] = Q;
arm_mat_init_f32(&_Q, 2, 2, Q_); // _A 矩阵是2X2的矩阵,里面的值是A
u = accz; // 将加速度
A[0] = 1; A[1] = dt;
A[2] = 0; A[3] = 1;
B[0] = 0.5*dt*dt * u;
B[1] = dt * u;
H[0] = 1;
H[1] = 0;
// 初始化矩阵实例
arm_mat_init_f32(&_A, 2, 2, A); // _A 矩阵是2X2的矩阵,里面的值是A
arm_mat_init_f32(&_A_T, 2, 2, A); // _A_T 矩阵是2X2的矩阵,里面的值是A
arm_mat_init_f32(&_B, 2, 1, B); // _B 矩阵是2X1的矩阵,里面的值是B
arm_mat_init_f32(&_H, 1, 2, H); // _H 矩阵是1X2的矩阵,里面的值是H
arm_mat_init_f32(&_HT, 2, 1, H); // _HT 矩阵是2X1的矩阵,里面的值是H
arm_mat_init_f32(&HP_HT, 1, 1, HPHT); //
arm_mat_init_f32(&hatx_, 2, 1, X_); // hatx_ 矩阵是2X1的矩阵,里面的值是X_
arm_mat_init_f32(&hatx, 2, 1, X); // hatx 矩阵是2X1的矩阵,里面的值是X
arm_mat_init_f32(&A_hatX, 2, 1, AX); // A_hatX 矩阵是2X1的矩阵,里面的值是AX
arm_mat_init_f32(&hatP_, 2, 2, P_); // hatP_ 矩阵是2X2的矩阵,里面的值是P_
arm_mat_init_f32(&hatP, 2, 2, P); // hatP 矩阵是2X2的矩阵,里面的值是P
arm_mat_init_f32(&A_hatP, 2, 2, AHATP);
arm_mat_init_f32(&A_hatPAT, 2, 2, AHATPAT);
arm_mat_init_f32(&Kk, 2, 1, K);
arm_mat_init_f32(&hatPk_HkT, 2, 1, PHT);
arm_mat_init_f32(&HkhatPk_, 1, 2, HK);
arm_mat_init_f32(&_KH, 2, 2, KH);
arm_mat_init_f32(&_I_KH, 2, 2, I_KH);
arm_mat_init_f32(&_I, 2, 2, I);
//kalman公式1: xk的先验估计
arm_mat_mult_f32(&_A, &hatx, &A_hatX); // A_hatX = _A * hatx
arm_mat_add_f32(&A_hatX, &_B, &hatx_); // 卡尔曼滤波公式1,hatx_是先验估计
//kalman公式2:误差协方差矩阵的先验估计
arm_mat_trans_f32(&_A, &_A_T); // A' (2x2)
arm_mat_mult_f32(&_A, &hatP, &A_hatP); // A_hatP = _A * hatP
arm_mat_mult_f32(&A_hatP, &_A_T, &A_hatPAT); // A_hatPAT = A_hatP * _A_T
arm_mat_add_f32(&A_hatPAT, &_Q, &hatP_); // hatP_ = A_hatPAT + Q
// kalman公式3:Kk = hatPk_ * HkT*(Hk*hatPk_HT + R)’
arm_mat_mult_f32(&_H, &hatP_, &HkhatPk_);
arm_mat_trans_f32(&_H, &_HT);
arm_mat_mult_f32(&HkhatPk_, &_HT, &HP_HT);
HPHT[0] += R;
HPHT[0] = 1 / HPHT[0];
arm_mat_mult_f32(&hatP_, &_HT, &hatPk_HkT);
arm_mat_mult_f32(&hatPk_HkT, &HP_HT, &Kk);
// 卡尔曼公式4
arm_mat_mult_f32(&_H, &hatx_, &HP_HT);
HPHT[0] = atti - HPHT[0];
arm_mat_mult_f32(&Kk, &HP_HT, &A_hatX);
arm_mat_add_f32(&hatx_, &A_hatX, &hatx);
// 卡尔曼公式5
arm_mat_mult_f32(&Kk, &_H, &_KH);
arm_mat_sub_f32(&_I, &_KH, &_I_KH);
arm_mat_mult_f32(&_I_KH, &hatP_, &hatP);
*pos_esti = hatx.pData[0];// 位置估计
*vel_esti = hatx.pData[1];
}
