数学建模笔记(十五):多元统计分析及R语言建模(判别分析、聚类分析、主成分分析、因子分析,含数据代码注释,均可供运行)
文章目录
- 一、多元数据的数学表达
-
- 1.多元分析资料的一般格式与矩阵化表示
- 2.数据特征(一元数据与多元数据的均值和方差)
- 二、R软件基本使用
-
- 1.向量创建(c函数)
- 2.行列合并(rbind,cbind)
- 3.矩阵创建与维数查询(注意行列优先,正态随机生成)
- 4.矩阵转置
- 5.矩阵的标量运算
- 6.矩阵运算(加减、乘法、点积点除)
-
- (一)加减
- (二)乘
- (三)点积点除
- 7.对角矩阵(diag函数介绍)
- 8.逆矩阵生成(solve函数)
- 9.矩阵的特征值与特征向量
- 10.矩阵行列求和、求均值,求方差
-
- (一)方法一(row**/col**)
- (二)方法二:apply(可求方差,也可自定义函数)
- 11.协方差矩阵与相关系数矩阵
- 12.文件读取
- 三、判别分析及R使用
-
- 1.概念
- 2.方法
- 3.线性判别分析(LDA)
-
- (一)步骤一:求 F i s h e r Fisher Fisher线性判别函数
- (二)步骤二:计算判别界值
- (三)步骤三:建立判别标准
- (四)例题:晴雨判断
- 4.距离判别
-
- (一)两总体距离判别——等差方阵(协方差矩阵相同),直线判别(LDA)
- (二)两总体距离判别——异差方阵(不同),二次判别(QDA)
- (三)例题:销售预测——两总体
- (四)多总体距离判别
- (五)例题:销售预测——多总体
- 5.Bayes判别法(概率性判别)
-
- (一)判别准则
- (二)例题:销售预测——概率判别
- 6.小结
- 四、聚类分析及R使用
-
- 1.概念
- 2.方法
- 3.聚类统计量(聚类原则)
- 4.系统聚类法
-
- (一)基本思想
- (二)类间距离计算方法
- (三)基本步骤
- (四)代码
- (五)例题:区域消费类型划分
- 5.kmeans聚类法
-
- (一)概念与原理
- (二)例题:对正态数据进行聚类
- 6.小结
- 五、主成分分析及R使用
-
- 1.基本思想与目的
- 2.数学表达与推导(如何确定主成分)
- 3.基本步骤
- 4.例题:区域消费类型划分——主成分分析法
- 5.小结
- 六、因子分析及R使用
-
- 1.与“主成分分析”的区别与联系
- 2.特点与用途
- 3.基本思想
- 4.因子分析模型(引入因子载荷矩阵)
- 5.基本步骤
- 6.因子载荷矩阵估计——主成分法(主因子法)
- 7.例题:公司业绩因子模型——两种方法估计因子载荷
-
- (一)原始评价指标
- (二)数据展示
- (三)代码展示
- 8.因子旋转
-
- (一)目的
- (二)方法
- (三)旋转前后对照
- 9.因子得分
-
- (一)目的
- (二)方法与结果对照
- (三)综合得分计算
一、多元数据的数学表达
1.多元分析资料的一般格式与矩阵化表示
数据类型
分类数据:是只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,是用文字来描述的,如男女;
顺序数据:是只能归于某一有序类别的非数字型数据。顺序数据虽然也是类别,但这些类别是有序的,如一等、二等;
数值数据:是按数字尺度测量的观察值,其结果表现为具体的数值。现实中所处理的大多数都是数值型数据;
2.数据特征(一元数据与多元数据的均值和方差)
二、R软件基本使用
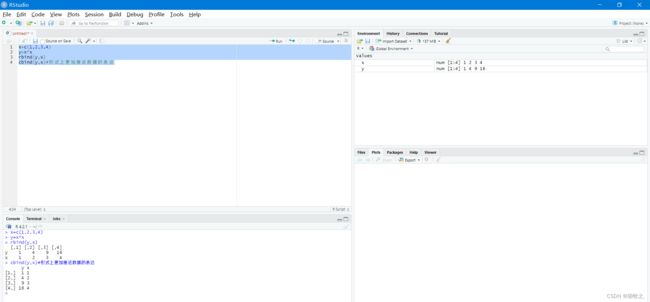
1.向量创建(c函数)
c函数,可以把多个元素或向量组合成一个向量
2.行列合并(rbind,cbind)
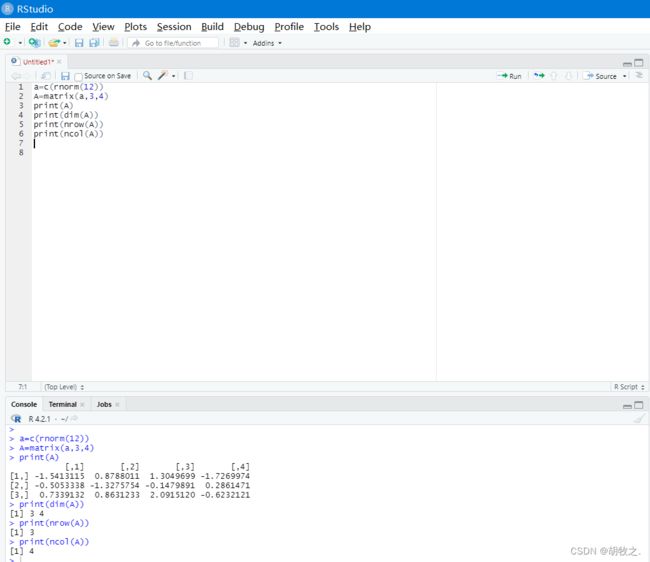
3.矩阵创建与维数查询(注意行列优先,正态随机生成)
默认为列优先,可添加参数调至行优先
正态分布随机生成矩阵:rnorm()
4.矩阵转置
5.矩阵的标量运算
6.矩阵运算(加减、乘法、点积点除)
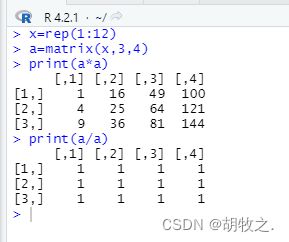
(一)加减
(二)乘
(三)点积点除
7.对角矩阵(diag函数介绍)
8.逆矩阵生成(solve函数)
9.矩阵的特征值与特征向量
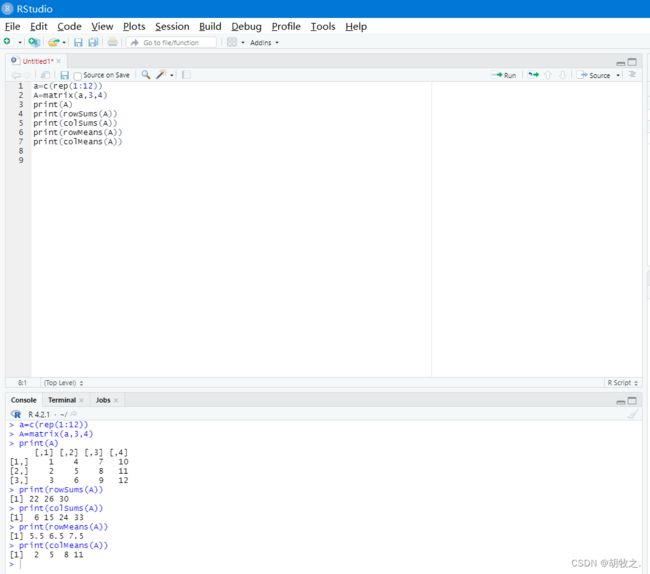
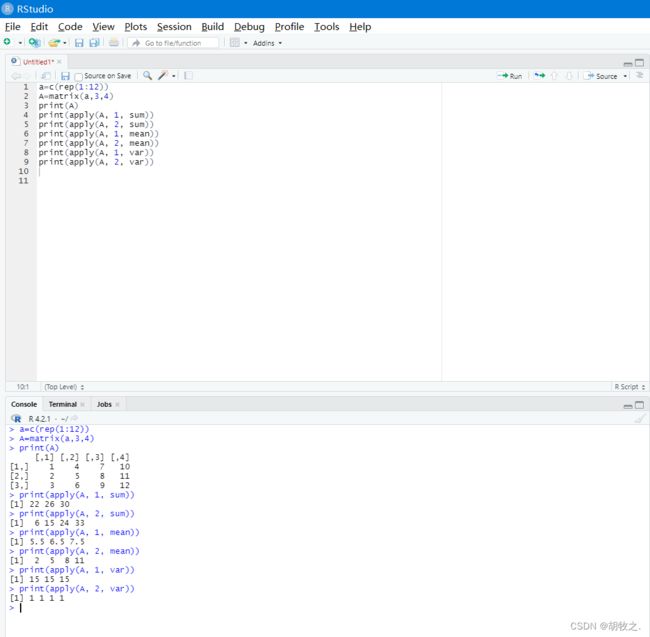
10.矩阵行列求和、求均值,求方差
(一)方法一(row**/col**)
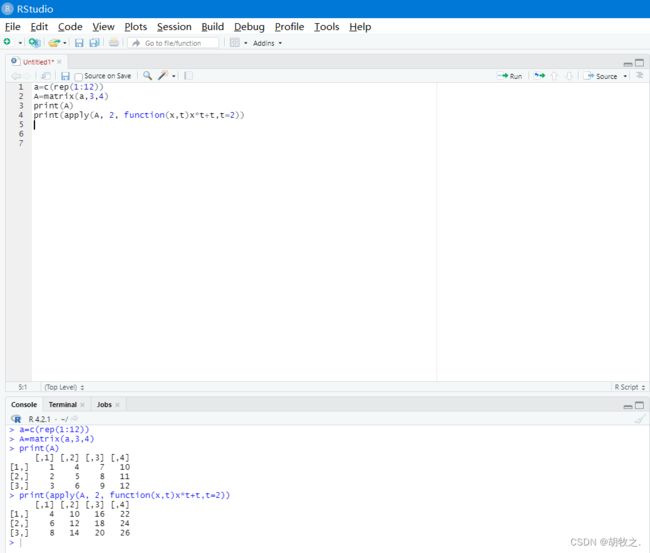
(二)方法二:apply(可求方差,也可自定义函数)
11.协方差矩阵与相关系数矩阵
12.文件读取
三、判别分析及R使用
1.概念
2.方法
3.线性判别分析(LDA)
只能线性划分,而且要求协方差阵要相同,有局限性
(一)步骤一:求 F i s h e r Fisher Fisher线性判别函数
思想为降维投影,找到一种合理的数据划分方式,也就是一个投影方向 a ⃗ \vec{a} a使得两均值 Y 1 ‾ = a ′ x 1 ‾ \overline{Y_1}=a^{'} \overline{x_1} Y1=a′x1与 Y 2 ‾ = a ′ x 2 ‾ \overline{Y_2}=a^{'} \overline{x_2} Y2=a′x2的标准化距离达到最大,换句话说就是令投影上同类样例的投影点尽可能靠近,异类样例的投影点尽可能远离。

下图中的 ∑ \sum ∑表示协方差矩阵,目标就是 ( d S d ) 2 (\frac{d}{S_d})^2 (Sdd)2最大


(二)步骤二:计算判别界值
(三)步骤三:建立判别标准
(四)例题:晴雨判断
数据(可供复制)
G x1 x2
1 -1.9 3.2
1 -6.9 0.4
1 5.2 2
1 5 2.5
1 7.3 0
1 6.8 12.7
1 0.9 -5.4
1 -12.5 -2.5
1 1.5 1.3
1 3.8 6.8
2 0.2 6.2
2 -0.1 7.5
2 0.4 14.6
2 2.7 8.3
2 2.1 0.8
2 -4.6 4.3
2 -1.7 10.9
2 -2.6 13.1
2 2.6 12.8
2 -2.8 10
代码(可供运行)
直接套用内部方法即可
d6.1=read.table("clipboard",header=T)#从剪切板读取,所以要先复制到剪切版
#header=T表示第一行为标题,避免错误处理
attach(d6.1)#绑定数据,如果未绑定路径索引,可能导致数据读取错误
plot(x1,x2)
text(x1,x2,G,adj=-0.5)#表示点所属类别,adj用于指定文本相对于给定坐标的对齐方式
library(MASS)#载入package MASS
(ld=lda(G~x1+x2))#lda即线性判别分析,此处直接建立判别函数,G为类别,~后为参数
Z=predict(ld)#对已有数据进行预测
newG=Z$class
cbind(G,Z$x,newG)#显示结果
(tab=table(G,newG))#建立混淆矩阵,直接看出有多少错判,对角线上的数据才是正确判定
sum(diag(prop.table(tab)))
#prop.table函数:频率统计函数
#prop.table(data):将data转换为百分比
#先转为百分比再对其对角线数据进行求和
predict(ld,data.frame(x1=8.1,x2=2.0))#对给定数据进行预测,注意要编为数据框
abline(1.2028/0.2248,0.1035/0.2248,col=2)#线性划分图示
4.距离判别
此处所说的距离不是指一般的欧式距离,而是采用马氏距离,可以避免不同量纲的影响
马氏距离
D ( X , G i ) D(X,G_i) D(X,Gi)表示的是样本 X X X与总体 G i G_i Gi的距离
μ i \mu_i μi表示总体 G i G_i Gi的均值
∑ i \sum_i ∑i表示总体 G i G_i Gi的协方差矩阵
( ) ′ ()' ()′表示转置
如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。

(一)两总体距离判别——等差方阵(协方差矩阵相同),直线判别(LDA)
式子有误,更正为: W ( X ) = 2 [ X − ( μ 1 + μ 2 ) 2 ] ′ ∑ − 1 ( μ 1 − μ 2 ) W(X)=2[X-\frac{(\mu_1+\mu_2)}{2}]^{'}\sum^{-1}(\mu_1-\mu_2) W(X)=2[X−2(μ1+μ2)]′∑−1(μ1−μ2)
(二)两总体距离判别——异差方阵(不同),二次判别(QDA)
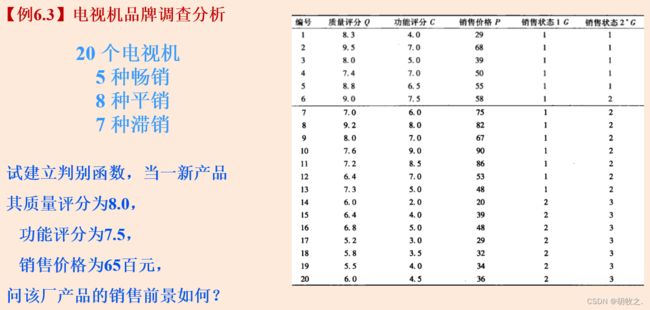
(三)例题:销售预测——两总体
数据(可供复制)
Q C P G1
8.3 4 29 1
9.5 7 68 1
8 5 39 1
7.4 7 50 1
8.8 6.5 55 1
9 7.5 58 1
7 6 75 1
9.2 8 82 1
8 7 67 1
7.6 9 90 1
7.2 8.5 86 1
6.4 7 53 1
7.3 5 48 1
6 2 20 2
6.4 4 39 2
6.8 5 48 2
5.2 3 29 2
5.8 3.5 32 2
5.5 4 34 2
6 4.5 36 2
代码(可供运行)
d6.2=read.table("clipboard",header=T)
d6.2
attach(d6.2)
par(mar=c(4,4,2,1),cex=0.75)
plot(Q,C);text(Q,C,G1,adj=-0.5)
plot(Q,P);text(Q,P,G1,adj=-0.5)
plot(C,P);text(C,P,G1,adj=-0.5)
library(MASS)
qd=qda(G1~Q+C+P);qd
cbind(G1,newG=predict(qd)$class)
predict(qd,data.frame(Q=8,C=7.5,P=65))
ld=lda(G1~Q+C+P);ld
W=predict(ld)
cbind(G1,Wx=W$x,newG=W$class)
predict(ld,data.frame(Q=8,C=7.5,P=65))
options(digits=3)#设置有效数字位数
(四)多总体距离判别
由于协方差矩阵相同,所以在下式中,可以将 ( X ′ ∑ − 1 X ) (X^{'}\sum^{-1}X) (X′∑−1X)视为常量,又因为负号的存在,所以实际上是根据 Z i Z_i Zi来判断距离
(五)例题:销售预测——多总体
数据(可供复制)
Q C P G2
8.3 4 29 1
9.5 7 68 1
8 5 39 1
7.4 7 50 1
8.8 6.5 55 1
9 7.5 58 2
7 6 75 2
9.2 8 82 2
8 7 67 2
7.6 9 90 2
7.2 8.5 86 2
6.4 7 53 2
7.3 5 48 2
6 2 20 3
6.4 4 39 3
6.8 5 48 3
5.2 3 29 3
5.8 3.5 32 3
5.5 4 34 3
6 4.5 36 3
代码(可供运行)
d6.3=read.table("clipboard",header=T)
attach(d6.3)
plot(Q,C);text(Q,C,G2,adj=-0.5,cex=0.75)
#adj,调整每个字符串的阅读方向(0=左对齐或下对齐,1=右对齐 或上对齐)
#cex,相对默认大小缩放倍数的数值
plot(Q,P);text(Q,P,G2,adj=-0.5,cex=0.75)
plot(C,P);text(C,P,G2,adj=-0.5,cex=0.75)
library(MASS)
ld=lda(G2~Q+C+P); ld
Z=predict(ld)
newG=Z$class
#Z中:class类别,posterior各类后验概率,x在各自映射向量上的映射值
cbind(G2,round(Z$x,3),newG)#round为四舍五入,此处表示对Z$x的数据保留3位小数
(tab=table(G2,newG))#混淆矩阵
diag(prop.table(tab,1))
sum(diag(prop.table(tab)))
plot(Z$x)
text(Z$x[,1],Z$x[,2],G2,adj=-0.8,cex=0.75)
predict(ld,data.frame(Q=8,C=7.5,P=65))
qd=qda(G2~Q+C+P); qd
Z=predict(qd)
newG=Z$class
cbind(G2,newG)
(tab=table(G2,newG))
sum(diag(prop.table(tab)))
predict(qd,data.frame(Q=8,C=7.5,P=65))
在线性判别中,有 n n n个总体就需要 n − 1 n-1 n−1个判别函数(投影方向)才可以分开


5.Bayes判别法(概率性判别)
(一)判别准则
概率判别
考虑在样本x出现后,x所属总体的后验概率
损失判别
(二)例题:销售预测——概率判别
以上方多总体例题为例
数据(可供复制)
Q C P G2
8.3 4 29 1
9.5 7 68 1
8 5 39 1
7.4 7 50 1
8.8 6.5 55 1
9 7.5 58 2
7 6 75 2
9.2 8 82 2
8 7 67 2
7.6 9 90 2
7.2 8.5 86 2
6.4 7 53 2
7.3 5 48 2
6 2 20 3
6.4 4 39 3
6.8 5 48 3
5.2 3 29 3
5.8 3.5 32 3
5.5 4 34 3
6 4.5 36 3
代码(可供运行)
d6.3=read.table("clipboard",header=T)
attach(d6.3)
library(MASS)
(ld1=lda(G2~Q+C+P,prior=c(1,1,1)/3))#prior,先验概率,此时表示3个总体先验概率相等
(ld2=lda(G2~Q+C+P,prior=c(5,8,7)/20))#此时表示三个总体的先验概率不相等(根据个数)
Z1=predict(ld1)
cbind(G2,round(Z1$x,3),newG=Z1$class)
Z2=predict(ld2)
cbind(G2,round(Z2$x,3),newG=Z2$class)
table(G2,Z1$class)
table(G2,Z2$class)
#根据混淆矩阵结果,发现无差异,侧面说明先验概率差异对结果影响不大
#不过根据后验概率结果,采用比例分配先验概率可能更好一些
round(Z1$post,3)
round(Z2$post,3)
predict(ld1,data.frame(Q=8,C=7.5,P=65))
predict(ld2,data.frame(Q=8,C=7.5,P=65))
6.小结
四、聚类分析及R使用
1.概念
判别分析中给定了具体的类,也就是所谓的Y值,所以我们也管这种分析称为有监督的学习;
聚类分析没有给定Y值,所以我们将这种分析称为无监督的学习
2.方法
3.聚类统计量(聚类原则)
对于样本,主要使用距离作为聚类统计量;
对于变量,经常使用相似系数作为聚类统计量
几类距离的介绍
一般明氏距离会带绝对值,所以式子写为: d i j ( q ) = [ ∑ k = 1 P ∣ x i k − x j k ∣ q ] 1 q d_{ij}(q)=[\sum_{k=1}^{P}|x_{ik}-x_{jk}|^{q}]^{\frac{1}{q}} dij(q)=[∑k=1P∣xik−xjk∣q]q1


以上的计算方法分别表示欧几里得距离、切比雪夫距离、绝对值距离(曼哈顿距离)、兰式距离、二进制距离、米科夫斯基距离(需交代 p p p值)
数据矩阵 X X X的格式为每行作为一个样品
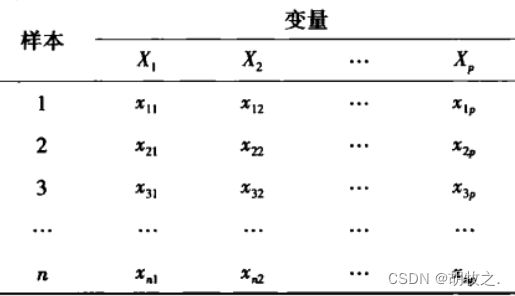
d i s t ( X ) dist(X) dist(X)默认使用欧式距离,且由于信息重复和对角线无意义所以只需标出矩阵一半的信息
通过调整参数 d i a g diag diag与 u p p e r upper upper,可以将这一部分信息显示出来
几类相似系数的介绍
4.系统聚类法
(一)基本思想
难点:重新计算类与类之间的距离
(二)类间距离计算方法

最短距离法以两个类中样本间最短距离作为两个类的距离
最长距离法以两个类中样本间最长距离作为两个类的距离
类平均法计算每个类的均值,以两个均值之间的距离作为两个类的距离
重心法找到每个类的重心,以两个重心之间的距离作为两个类的距离
(三)基本步骤
print(cbind(hc$merge,hc$height))
可以展示出分类的过程,关于上图的解释是先向4与5合并,再将1并入该类,再并入2,最后并入3

通过作图可以更加清晰表明合并顺序,每次合并都将消除一个类,如果想得知划分为特定类数的划分方式,只需根据合并次数
比如初始为 n n n个样本,欲划分为 3 3 3类,只需看在第 n − 3 n-3 n−3次合并后的结果
(四)代码
x1=c(5,7,3,6,6)
x2=c(7,1,2,5,6)
plot(x1,x2)
text(x1,x2,c(1:5),adj=-0.5)
X=cbind(x1,x2)#按列结合,结果为5个样品,每个样品有两个指标
dist(X)
dist(X,diag=TRUE)
dist(X,method="manhattan")
dist(X,method="minkowski",p=1)
dist(X,upper=TRUE)
dist(X,method="minkowski",p=2)
hc=hclust(dist(X),"single")
print(cbind(hc$merge,hc$height))
plot(hc)
hc<-hclust(dist(X),"complete")
print(cbind(hc$merge,hc$height))
plot(hc)
hc<-hclust(dist(X),"average")
print(cbind(hc$merge,hc$height))
plot(hc)
hc<-hclust(dist(X),"ward")
print(cbind(hc$merge,hc$height))
plot(hc)
(五)例题:区域消费类型划分
数据(可供复制)
X1 X2 X3 X4 X5 X6 X7 X8
北京 4934.05 1512.88 981.13 1294.07 2328.51 2383.96 1246.19 649.66
天津 4249.31 1024.15 760.56 1163.98 1309.94 1639.83 1417.45 463.64
河北 2789.85 975.94 546.75 833.51 1010.51 895.06 917.19 266.16
山西 2600.37 1064.61 477.74 640.22 1027.99 1054.05 991.77 245.07
内蒙古 2824.89 1396.86 561.71 719.13 1123.82 1245.09 941.79 468.17
辽宁 3560.21 1017.65 439.28 879.08 1033.36 1052.94 1047.04 400.16
吉林 2842.68 1127.09 407.35 854.8 873.88 997.75 1062.46 394.29
黑龙江 2633.18 1021.45 355.67 729.55 746.03 938.21 784.51 310.67
上海 6125.45 1330.05 959.49 857.11 3153.72 2653.67 1412.1 763.8
江苏 3928.71 990.03 707.31 689.37 1303.02 1699.26 1020.09 377.37
浙江 4892.58 1406.2 666.02 859.06 2473.4 2158.32 1168.08 467.52
安徽 3384.38 906.47 465.68 554.44 891.38 1169.99 850.24 309.3
福建 4296.22 940.72 645.4 502.41 1606.9 1426.34 1261.18 375.98
江西 3192.61 915.09 587.4 385.91 732.97 973.38 728.76 294.6
山东 3180.64 1238.34 661.03 708.58 1333.63 1191.18 1027.58 325.64
河南 2707.44 1053.13 549.14 626.55 858.33 936.55 795.39 300.19
湖北 3455.98 1046.62 550.16 525.32 903.02 1120.29 856.97 242.82
湖南 3243.88 1017.59 603.18 668.53 986.89 1285.24 869.59 315.82
广东 5056.68 814.57 853.18 752.52 2966.08 1994.86 1444.91 454.09
广西 3398.09 656.69 491.03 542.07 932.87 1050.04 803.04 277.43
海南 3546.67 452.85 519.99 503.78 1401.89 837.83 819.02 210.85
重庆 3674.28 1171.15 706.77 749.51 1118.79 1237.35 968.45 264.01
四川 3580.14 949.74 562.02 511.78 1074.91 1031.81 690.27 291.32
贵州 3122.46 910.3 463.56 354.52 895.04 1035.96 718.65 258.21
云南 3562.33 859.65 280.62 631.7 1034.71 705.51 673.07 174.23
西藏 3836.51 880.1 271.29 272.81 866.33 441.02 628.35 335.66
陕西 3063.69 910.29 513.08 678.38 866.76 1230.74 831.27 332.84
甘肃 2824.42 939.89 505.16 564.25 861.47 1058.66 768.28 353.65
青海 2803.45 898.54 484.71 613.24 785.27 953.87 641.93 331.38
宁夏 2760.74 994.47 480.84 645.98 859.04 863.36 910.68 302.17
新疆 2760.69 1183.69 475.23 598.78 890.3 896.79 736.99 331.8
由于版本更新过快导致不同版本间命令的不兼容,高版本中无法导入 m v s t a t s mvstats mvstats包
#适用于低版本
d7.2=read.table("clipboard",header=T)
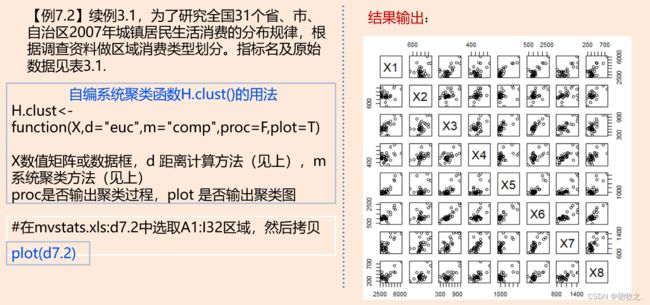
plot(d7.2)
library(mvstats)#高版本下无法运行,由于版本更新过快导致不同版本间命令的不兼容
H.clust(d7.2,"euclidean","single",plot=T)
H.clust(d7.2,"euclidean","complete",plot=T)
H.clust(d7.2,"euclidean","median",plot=T)
H.clust(d7.2,"euclidean","average",plot=T)
H.clust(d7.2,"euclidean","centroid",plot=T)
H.clust(d7.2,"euclidean","ward",plot=T)
将函数替换即可,直接使用hclust方法
#适用于高版本
d7.2=read.table("clipboard",header=T)
plot(d7.2)
#library(mvstats) 高版本下无法运行,由于版本更新过快导致不同版本间命令的不兼容
#hclust同样可以实现
plot(hclust(dist(d7.2),method = "single"),hang=-1)#最短距离法
plot(hclust(dist(d7.2),method = "complete"),hang=-1)#最长距离法
plot(hclust(dist(d7.2),method = "median"),hang=-1)#中间距离法
plot(hclust(dist(d7.2),method = "average"),hang=-1)#类平均法
plot(hclust(dist(d7.2),method = "centroid"),hang=-1)#重心法
plot(hclust(dist(d7.2),method = "ward"),hang=-1)#Ward法
5.kmeans聚类法
(一)概念与原理
n n n个对象要分为 k k k类
优点是适合对大型数据集进行分类
缺点是对k取值比较敏感

(二)例题:对正态数据进行聚类
直接调用内部方法
代码(可供运行)
x1=matrix(rnorm(1000,mean=0,sd=0.3),ncol=10)#共100个样品,每个样品有10个指标
x2=matrix(rnorm(1000,mean=1,sd=0.3),ncol=10)
x=rbind(x1,x2)
cl=kmeans(x,2)#,给定了k值(聚类个数)
pch1=rep("1",100)
pch2=rep("2",100)
plot(x,col=cl$cluster,pch=c(pch1,pch2),cex=0.7)
points(cl$centers,col=3,pch="*",cex=3)
#-------------------------------------------------
#增加数据量
x1=matrix(rnorm(10000,mean=0,sd=0.3),ncol=10)
x2=matrix(rnorm(10000,mean=1,sd=0.3),ncol=10)
x=rbind(x1,x2)
cl=kmeans(x,2)
pch1=rep("1",1000)
pch2=rep("2",1000)
plot(x,col=cl$cluster,pch=c(pch1,pch2),cex=0.7)
#col指定颜色,pch指定不同散点情况,cex指定大小
#此处以类别号作为颜色序号
#关于pch1中1000的由来,其实这个表示的是样品数目
points(cl$centers,col=3,pch ="*",cex=3)
#cl$centers表示类的重心
6.小结
五、主成分分析及R使用
1.基本思想与目的
要求是原始指标之间要具备一定的相关性,然后用原始指标构造出相互无关的综合指标作为新的指标

2.数学表达与推导(如何确定主成分)
成分个数与变量个数一致


假设 ∑ \sum ∑为 X X X的协方差阵
u 1 ′ u_1^{'} u1′为 u 1 u_1 u1的转置
在一维情况下, c c c为常数: v a r ( c x ) = c 2 v a r ( x ) var(cx)=c^2var(x) var(cx)=c2var(x)
在 p p p维情况下, a a a为矩阵: v a r ( a ′ x ) = a ′ v a r ( x ) a = a ′ ∑ a var(a^{'} x)=a^{'}var(x)a=a^{'}\sum a var(a′x)=a′var(x)a=a′∑a
目标是令上式中 y 1 y_1 y1具有最大的方差,首先要给定一定条件的限制,否则不存在最大的情况,所以不妨再假设 u 1 ′ u 1 u_1^{'}u_1 u1′u1结果为单位矩阵(不唯一)
此时就得到 v a r ( y 1 ) = v a r ( u 1 ′ x ) = u 1 ′ ∑ u 1 var(y_1)=var(u_1^{'}x)=u_1^{'} \sum u_1 var(y1)=var(u1′x)=u1′∑u1
条件极值问题——一般方法:拉格朗日乘数法
L ( u 1 , λ ) = u 1 ′ ∑ u 1 − λ ( u 1 ′ u 1 − 1 ) L(u_1,\lambda)=u_1^{'}\sum u_1-\lambda(u_1^{'}u_1-1) L(u1,λ)=u1′∑u1−λ(u1′u1−1)

最终结果,求的第一主成分就是特征根 λ \lambda λ,那么 u 1 u_1 u1就是最大特征根对应的单位特征向量
如果第一主成分不足以代表原来的 P P P个指标,就还需要求出第二主成分,为了有效反映原来信息,第一主成分所包含的信息不需要在第二主成分中出现,要求 C O V ( y 1 , y 2 ) = u 1 ′ ∑ u 2 = 0 COV(y_1,y_2)=u_1^{'}\sum u_2=0 COV(y1,y2)=u1′∑u2=0,以此类推求出其余主成分
3.基本步骤
4.例题:区域消费类型划分——主成分分析法
目标是确定主成分,然后依照主成分进行排名并作图
数据(可供复制)
X1 X2 X3 X4 X5 X6 X7 X8
北京 4934.05 1512.88 981.13 1294.07 2328.51 2383.96 1246.19 649.66
天津 4249.31 1024.15 760.56 1163.98 1309.94 1639.83 1417.45 463.64
河北 2789.85 975.94 546.75 833.51 1010.51 895.06 917.19 266.16
山西 2600.37 1064.61 477.74 640.22 1027.99 1054.05 991.77 245.07
内蒙古 2824.89 1396.86 561.71 719.13 1123.82 1245.09 941.79 468.17
辽宁 3560.21 1017.65 439.28 879.08 1033.36 1052.94 1047.04 400.16
吉林 2842.68 1127.09 407.35 854.8 873.88 997.75 1062.46 394.29
黑龙江 2633.18 1021.45 355.67 729.55 746.03 938.21 784.51 310.67
上海 6125.45 1330.05 959.49 857.11 3153.72 2653.67 1412.1 763.8
江苏 3928.71 990.03 707.31 689.37 1303.02 1699.26 1020.09 377.37
浙江 4892.58 1406.2 666.02 859.06 2473.4 2158.32 1168.08 467.52
安徽 3384.38 906.47 465.68 554.44 891.38 1169.99 850.24 309.3
福建 4296.22 940.72 645.4 502.41 1606.9 1426.34 1261.18 375.98
江西 3192.61 915.09 587.4 385.91 732.97 973.38 728.76 294.6
山东 3180.64 1238.34 661.03 708.58 1333.63 1191.18 1027.58 325.64
河南 2707.44 1053.13 549.14 626.55 858.33 936.55 795.39 300.19
湖北 3455.98 1046.62 550.16 525.32 903.02 1120.29 856.97 242.82
湖南 3243.88 1017.59 603.18 668.53 986.89 1285.24 869.59 315.82
广东 5056.68 814.57 853.18 752.52 2966.08 1994.86 1444.91 454.09
广西 3398.09 656.69 491.03 542.07 932.87 1050.04 803.04 277.43
海南 3546.67 452.85 519.99 503.78 1401.89 837.83 819.02 210.85
重庆 3674.28 1171.15 706.77 749.51 1118.79 1237.35 968.45 264.01
四川 3580.14 949.74 562.02 511.78 1074.91 1031.81 690.27 291.32
贵州 3122.46 910.3 463.56 354.52 895.04 1035.96 718.65 258.21
云南 3562.33 859.65 280.62 631.7 1034.71 705.51 673.07 174.23
西藏 3836.51 880.1 271.29 272.81 866.33 441.02 628.35 335.66
陕西 3063.69 910.29 513.08 678.38 866.76 1230.74 831.27 332.84
甘肃 2824.42 939.89 505.16 564.25 861.47 1058.66 768.28 353.65
青海 2803.45 898.54 484.71 613.24 785.27 953.87 641.93 331.38
宁夏 2760.74 994.47 480.84 645.98 859.04 863.36 910.68 302.17
新疆 2760.69 1183.69 475.23 598.78 890.3 896.79 736.99 331.8
基础安装包里有princomp()函数可以做主成分分析,factanal()函数可以做因子分析
par()函数介绍:调整默认绘图参数
碎石图介绍
碎石图是将特征根以图示形式展示,主要用于辅助判断因子个数。如果不确定提取多少个因子,此时可以参考碎石图结果判断因子个数。
代码(可供运行,含手动实现代码替代导入包)
X=read.table("clipboard",header=T)
cor(X)#相关系数矩阵,默认数据之间的皮埃尔相关系数
PCA=princomp(X,cor=T)#主成分分析,且使用的是相关矩阵
#主成分分析可以使用协方差矩阵也可以使用相关矩阵,函数标明即可,结果可能有差异
#相关系数是协方差标准化的结果,所以此时用cor无需标准化,但使用协方差需要进行标准化
PCA#特征值开根号结果
options(digits=3)#修改有效位数
summary(PCA)#从数据中获取描述性统计量,此处包括标准差、方差比例、累计占比
PCA$loadings#主成分载荷,也就是主成分与原始变量之间的相关系数
#SS loadings包含与主成分相关联的特征值,指的是与特定主成分相关联的标准化后的方差值
par(mar=c(4,4,2,1),cex=0.75)#par函数作用是调整默认的绘图参数
#mar,设置图形空白边界行数,默认为mar=c(5.1,4.1,4.1,2.1)
#cex,设置文本和符合的尺度,默认为cex=1
screeplot(PCA,type="lines")#碎石图选定因子个数
eig=eigen(cor(X));eig#另外一种方法是选出特征根大于1的因子,依然是前两个
PCA$scores[,1:2]#主成分得分,根据碎石图选定了前两个因子,再加权求出各自的值
#不使用包,手动计算进行排名并排序
comp1=PCA$scores[,1]
comp2=PCA$scores[,2]
c=eig$values[1]/(eig$values[1]+eig$values[2])*comp1+eig$values[2]/(eig$values[1]+eig$values[2])*comp2
rank=rank(c)
sort=cbind(comp1,comp2,c,rank)
sort=sort[order(sort[,4]),]
View(sort)
#------以下内容高版本不兼容,用于主成分排名----------
library(mvstats)
princomp.rank(PCA,m=2)#主成分排名,总得分是根据特征值进行加权平均计算,然后依次进行排名
princomp.rank(PCA,m=2,plot=T)#主成分排名作图
5.小结
六、因子分析及R使用
Factor Analysis
1.与“主成分分析”的区别与联系
2.特点与用途
3.基本思想
4.因子分析模型(引入因子载荷矩阵)
X X X为原始变量, E ( x ) = 0 E(x)=0 E(x)=0说明可能已经经过了标准化,所以得到的协方差矩阵与相关矩阵相同
F F F为公共因子,不可观测, c o v ( F ) = 1 cov(F)=1 cov(F)=1说明公共因子之间是不相关的
ε \varepsilon ε为特殊因子

A A A,也就是所谓的因子载荷矩阵


5.基本步骤
6.因子载荷矩阵估计——主成分法(主因子法)
主成分法求解因子载荷矩阵
根据矩阵表示,有 X = A F + ε X=AF+\varepsilon X=AF+ε
由于 A F AF AF与 ε \varepsilon ε不相关,所以对式子两边同时取协方差矩阵:
c o v ( X ) = c o v ( A F ) + c o v ( ε ) cov(X)=cov(AF)+cov(\varepsilon) cov(X)=cov(AF)+cov(ε)
⇓ \Downarrow ⇓
R = A A ′ + D R=AA^{'}+D R=AA′+D( R R R为x相关矩阵, D D D为 ε \varepsilon ε协方差阵,一个对角阵)
⇓ \Downarrow ⇓
A = ( λ 1 l 1 , λ 2 l 2 … … λ m l m ) A=(\sqrt{\lambda_1}l_1,\sqrt{\lambda_2}l_2……\sqrt{\lambda_m}l_m) A=(λ1l1,λ2l2……λmlm)

7.例题:公司业绩因子模型——两种方法估计因子载荷
(一)原始评价指标
(二)数据展示
x1 x2 x3 x4 x5 x6
冀东水泥 33.8 34.75 0.67 59.77 15.49 16.35
大同水泥 27.54 28.04 2.36 35.29 -20.96 -46.45
四川双马 22.86 23.47 0.61 42.83 5.48 -49.22
牡丹江 19.05 19.95 1 48.51 -12.32 -65.99
西水股份 20.84 21.17 1.08 48.45 65.09 54.81
狮头股份 28.14 28.84 2.51 24.52 -6.43 -15.94
太行股份 30.45 31.13 1.02 46.14 6.57 -16.59
海螺水泥 36.29 36.96 0.27 58.31 70.85 117.59
尖峰集团 16.94 17.26 0.61 52.04 9.03 -94.05
四川金顶 28.74 29.4 0.6 65.46 -33.97 -55.02
祁连山 33.31 34.3 1.17 45.8 12.18 39.46
华新水泥 25.08 26.12 0.64 69.35 22.38 -10.2
福建水泥 34.51 35.44 0.38 61.61 23.91 -163.99
天鹅股份 25.52 26.73 1.1 47.02 -4.51 -68.79
(三)代码展示
X=read.table("clipboard",header=T)
cor(X)
screeplot(princomp(X,cor=T),type="lines")#主成分分析确定因子个数
(FA0=factanal(X,3,rot="none"))#基于极大似然方法求解
#输入
#factanal(X,factors,scores=c("none", "regression","Bartlett"),rotation="varimax", ...)
#X是用于因子分析的数据,可以为矩阵或数据框
#factors表示要生成的因子的个数,建议先用主成分分析法确定个数
#scores表示计算得分的方式:回归方法、最小二乘法
#rotation表示因子旋转的方式,默认使用varimax最大化方差旋转
#输出
#loading即因子载荷
#Cumulative Var累计方差,可以看出已满足要求
(Fa1=factanal(X,3,rot="varimax"))#加上因子旋转,对比效果
Fa1=factanal(X,3,scores="regression")
Fa1$scores
factanal.rank(Fa1,plot=T)#因子综合得分作图与排名,计算方式与主成分方法一致
#不使用包,手动计算进行排名并排序
#值得注意的是,求综合评价的方法不唯一
#只要是涉及定性分析的方法需要人为地确定一些因素,或多或少都带有点主观性
comp1=Fa1$scores[,1]
comp2=Fa1$scores[,2]
comp3=Fa1$scores[,3]
c=(0.333*comp1+0.3*comp2+0.228*comp3)/0.861
rank=rank(c)
sort=cbind(comp1,comp2,comp3,c,rank)
sort=sort[order(sort[,5]),]
View(sort)
biplot(Fa1$scores,Fa1$loadings)
#双标图
library(mvstats)
#factpc=function(X,m=2,scores=c("none","regression"),rotation="varimax")
#factpc()在mvstats包中
(Fac=factpc(X,3))
Fac1=factpc(X,3,scores="regression")
Fac1$scores
8.因子旋转
(一)目的
(二)方法
(三)旋转前后对照
![]()
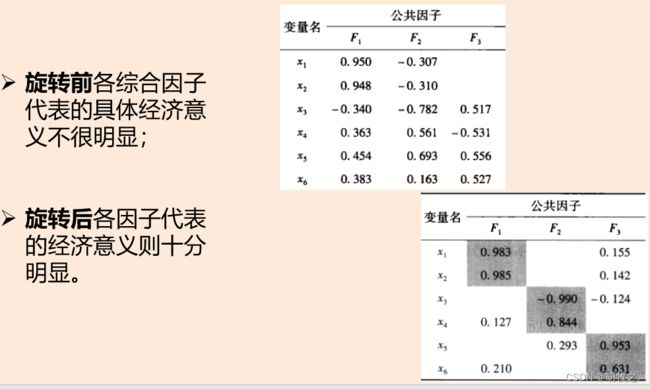
个人理解:通过旋转增强了因子的实际意义,以便于进行专业角度的分析
9.因子得分
(一)目的
(二)方法与结果对照
factpc()函数在mvstats包中,高版本无法运行
(三)综合得分计算
值得注意的是,求综合评价的方法不唯一
只要是涉及定性分析的方法需要人为地确定一些因素,或多或少都带有点主观性
所以在上方代码中,借助factanal.rank()计算与手动计算的结果有差异
手动计算的思路是以旋转后的方差进行加权平均计算