利用主成分分析(PCA)法对基金进行排名
利用主成分分析(PCA)法对基金进行排名
一、基金指标的计算
1、年化收益率(R)
日基金收益率: r t = N A V t − N A V t − 1 N A V t − 1 r_t=\frac {NAV_t-NAV_{t-1}}{NAV_{t-1}} rt=NAVt−1NAVt−NAVt−1
N A V NAV NAV表示的是基金的复权净值,基金的日收益率就等于基金当日净值减去前一日净值除以前一日净值。
年化收益率: R = [ ∏ 1 t ( 1 + r n ) ] 250 n − 1 R=\left[\prod_1^t(1+r_n)\right]^\frac{250}{n}-1 R=[∏1t(1+rn)]n250−1
∏ \prod ∏表示连乘符号,上式中的 ∏ 1 t ( 1 + r n ) \prod_1^t(1+r_n) ∏1t(1+rn)相当于 ( 1 + r 1 ) ( 1 + r 2 ) . . . ( 1 + r n ) (1+r_1)(1+r_2)...(1+r_n) (1+r1)(1+r2)...(1+rn)。我们可以将上式转化成 ( 1 + R ) n 250 = ∏ 1 t ( 1 + r n ) \left(1+R\right)^\frac{n}{250}=\prod_1^t(1+r_n) (1+R)250n=∏1t(1+rn)。假设初始净值为1,则左边是用年化收益率计算的最终净值,右边是用日收益率计算的最终净值,利用净值相等即可计算出年化收益率指标。 n 250 \frac{n}{250} 250n是表示的是年数,n表示的是日收益率的个数,或者交易天数。
问:在年化收益率的计算公式中,250的来源?
这是因为基金一年的交易时间大约为250天,其余时间都是不能交易的。
2、超额收益率(Alpha)
超额收益率: α = r i − β r m \alpha=r_i-\beta r_m α=ri−βrm
* r i r_i ri基金i的实际收益率;
* r m r_m rm市场的收益率。
超额收益率是指超过预期(市场)收益率的收益率,这部分收益率可以看成是基金经理创造的收益率。从上述公式可以看出,超额收益率是假设基金i的收益率与市场收益率存在线性关系,我们只需要利用最小二乘法,将基金i的实际收益率和市场收益率进行回归。得到的常数项,便是我们的超额收益率。
3、调整的在险值(MVaR)
MVaR的计算和推导较为复杂,这里直接引用原作者的公式。该值是基金的最大可能损失。
M V a R α = μ + ( z c + 1 6 ( z c 2 − 1 ) S + 1 24 ( z c 3 − 3 z c ) K − 1 36 ( 2 z c 3 − 5 z c ) S 2 ) σ MVaR_\alpha=\mu+(z_c+\frac{1}{6}(z_c^2−1)S+\frac{1}{24}(z_c^3−3z_c)K−\frac{1}{36}(2z_c^3−5z_c)S^2)\sigma MVaRα=μ+(zc+61(zc2−1)S+241(zc3−3zc)K−361(2zc3−5zc)S2)σ
其中 z c z_c zc,是正态分布在置信度为α%下的临界值。而 μ、σ、S、K则为样本收益率分布的均值,标准差,偏度,峰度。
4、最大回撤率(MD)
最大回撤率: M D = M a x ( N A V ) − M i n ( N A V ) M a x ( N A V ) MD=\frac{Max(NAV)-Min(NAV)}{Max(NAV)} MD=Max(NAV)Max(NAV)−Min(NAV)
在一段区间内,基金净值从最大值跌到最小值时的下降幅度。
5、平均回撤(AD)
每日回撤: D D t = M a x ( N A V ) − N A V t M a x ( N A V ) DD_t=\frac{Max(NAV)-NAV_t}{Max(NAV)} DDt=Max(NAV)Max(NAV)−NAVt
平均回撤: A D = 1 n ∑ i n D D t AD=\frac{1}{n}\sum_i^nDD_t AD=n1∑inDDt
样本所有回撤的平均值。每日回撤用当日净值计算,而非最小净值。与最大回撤相比,每日回撤将最小净值( M i n ( N A V ) Min(NAV) Min(NAV))替换成了当日净值( N A V t NAV_t NAVt)。
6、负向收益波动率(LPM)
把样本的负数收益率单独提取出来,并计算其标准差。该指标越大,说明负向波动越大,亏损的幅度越大。
7、收益波动率(SIGMA)
样本的标准差。
8、风险调整后的收益率指标
H_Mvar (R/exp(MVaR))*为什么不是直接除以MvaR?
CR (卡玛比率, R/abs(MD))
H_Ad (R/abs(AD))
SoR (索提诺比率, R/LPM)
SR (夏普比率, R/SIGMA)
A_Mvar (Alpha/exp(MVaR))*为什么不是直接除以MvaR?
A_Md (Alpha/abs(MD))
A_Ad (Alpha/abs(AD))
XR (X比率, Alpha/LPM)
IR (信息比率, Alpha/SIGMA)
上面计算的年化收益率(R)和超额收益率(Alpha)都没有考虑风险的因素,因此可以将上述年化收益率(R)和超额收益率(Alpha)等收益率指标分别除以调整在险值(MVaR)、最大回撤(MD)、平均回撤(AD)、负向收波动率(LPM)、收益波动率(SIGMA)等风险指标,得到单位风险下的收益率指标。
二、指标计算代码
2.1 数据读取
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
fund_data = pd.read_csv("fund_data.csv",index_col = 0)#读取数据
fund_data["endDate"]=pd.to_datetime(fund_data["endDate"])#将基金净值日期转化成时间格式
# print(fund_data.info())#查看字段信息
fund_id = list(set(fund_data["secID"].tolist()))#提取基金数据表中的各个基金的编码,可删除重复值
*原始数据表中各字段的含义
| 名称 | 类型 | 描述 |
|---|---|---|
| secID | str | 内部编码 |
| ticker | str | 基金代码 |
| secShortName | str | 基金中文简称 |
| endDate | str | 净值日期 |
| NAV | float | 单位净值(元) |
| publishDate | str | 净值公布日期 |
| currencyCd | str | 计量货币,"CNY"为人民币,"HKD"为港币,"USD"为美元。对应DataAPI.SysCodeGet.codeTypeID=10004。 |
| ACCUM_NAV | float | 累计净值(元) |
| ADJUST_NAV | float | 复权净值(元) |
| navChg | float | 单位净值涨跌 |
| navChgPct | float | 单位净值涨跌幅(%) |
| adjNavChgPct | float | 复权净值涨跌幅(%) |
| partyID | int | 基金公司ID |
| partyShortName | str | 基金公司简称 |
本文调取了2017年9月1日至2022年8月31日,共61个混合型上市开放式基金。
2.2 基金日收益率计算
#计算各基金的收益率
def Calc_Returns(fund_id,fund_data):
'''
Parameters
----------
fund_id : 基金编码目录.
fund_data : 基金数据清单.
Returns
-------
returns : 各基金的收益率.
'''
returns = {}
for singleid in fund_id:
temp = fund_data[fund_data['secID']==singleid]#提取单个基金的信息
temp = temp.set_index('endDate')#将基金净值的日期设置为索引
value = temp['ADJUST_NAV']#获取基金的复权净值
# new_index = value.index[1:]#提取日期
ret = (value-value.shift(1))/value.shift(1)#计算收益率
ret = ret.dropna()#删除空值
returns.update({singleid:ret})
return returns
2.3 基金年华收益率计算
#计算年化收益率
def annual_yield(fund_ret):
'''
Parameters
----------
fund_ret : 基金收益率.
Returns
-------
annret : 基金2017年9月至2022年8月的年华收益率.
'''
n=len(fund_ret)
endvalue=1#设初始价值为1
for i in range(n):
endvalue=endvalue*(1+fund_ret[i])
#计算年华收益率
annret=endvalue**(250/n)-1#一年大约有250个交易日
return annret
2.4 基金超额收益率(Alpha)计算
#计算超额收益率Alpha
def Calc_Alpha(fund_ret,index_ret):
'''
Parameters
----------
fund_ret : 基金收益率.
index_ret : 指数收益率,这个指标我们在后面计算.
Returns
-------
alpha : 基金的超额收益率.
'''
n = len(fund_ret)#基金个数
beta = float(((fund_ret*index_ret).sum() - n*(fund_ret.mean())*(index_ret.mean()))) / ((index_ret**2).sum() - n*((index_ret.mean())**2))
alpha = fund_ret.mean() - beta*index_ret.mean()
return alpha
'''
n = len(fund_ret)#基金个数
beta = float(((fund_ret*index_ret).sum() - n*(fund_ret.mean())*(index_ret.mean()))) / ((index_ret**2).sum() - n*((index_ret.mean())**2))
alpha = fund_ret.mean() - beta*index_ret.mean()
return alpha
说明1,index_ret的来源:
基金的超额收益率计算代码中多了一个index_ret指标,该指标表示的是61支基金的平均收益率,我们将在后面计算。
说明2,为什么没用OLS回归计算beta( β \beta β)值:
代码中beta值是直接利用公式计算出来的,其公式就是根据最小二乘法进行推导的,因此同利用线性回归计算的结果相同。最小二乘法中beta的计算公式为: β = ∑ x y − n x ˉ y ˉ ∑ x 2 − n x ˉ 2 \beta=\frac{\sum xy-n\bar x\bar y}{\sum x^2-n\bar x^2} β=∑x2−nxˉ2∑xy−nxˉyˉ,其中 x ˉ 和 y ˉ \bar x和\bar y xˉ和yˉ代表的是平均值。
2.5 调整的在险值(MVaR)计算
# MVaR
def Calc_MVaR(fundRet,level):
'''
Parameters
----------
fundRet : 基金收益率.
level : 置信水平.
Returns
-------
MVaR : 调整的在险值.
'''
mu = fundRet.mean()#均值
sigma = fundRet.std()#标准差
S = fundRet.skew()#偏度
K = fundRet.kurtosis()#峰度
z = fundRet.quantile(level)#求分位数,如果level为1%,则表示有1%的数据都小于z
MVaR = mu + (z + (1.00/6)*(z**2 -1)*S + (1.00/24)*(z**3-3*z)*K - (1.00/36)*(2*(z**3)-5*z)*(S**2))*sigma
return MVaR
偏度(K):是统计数据分布非对称程度的数字特征。定义上偏度是样本的三阶标准化矩。
K = 1 n ( X − μ σ ) 3 K=\frac{1}{n}\left(\frac{X-\mu}{\sigma}\right)^3 K=n1(σX−μ)3
正态分布的偏度为零(关于均值左右对称),右偏分布(也叫正偏分布,其偏度>0),左偏分布(也叫负偏分布,其偏度<0)。
峰度(z):表示概率密度分布曲线在平均值处峰值高低的特征数。直观看来,峰度反映了峰部的尖度。随机变量的峰度计算方法为:
K = 1 n ( X − μ σ ) 4 K=\frac{1}{n}\left(\frac{X-\mu}{\sigma}\right)^4 K=n1(σX−μ)4
正态分布的峰度值为3,厚尾的分布峰度值大于3,瘦尾的分布峰度值小于3。
2.6 最大回撤(MD)计算
# 最大回撤 MD
def Calc_MD(netvalue):
'''
Parameters
----------
netvalue : 基金净值
Returns
-------
基金的最大回撤率.
'''
netvalue = np.array(netvalue)
length = len(netvalue)
drawdown = []
py =netvalue[0]
for i in range(1,length):
px = netvalue[i]
py = max(netvalue[:i])
drawdown.append(1-(px/py))
return max(drawdown)
2.7 平均回撤(AD)计算
# 平均回撤 AD
def Calc_AD(netvalue):
'''
Parameters
----------
netvalue : 基金净值.
Returns
-------
AD : 平均回撤.
'''
netvalue = np.array(netvalue)
N = len(netvalue)
AD = 0
py =netvalue[0]
for i in range(1,N):
px = netvalue[i]
py = max(netvalue[:i])
DD = (1-(float(px)/py))
AD = AD + DD*(0.9**(N-i))#此处用的是指数加权平均
return AD
此处计算平均回撤时,并没有使用回撤的算术平均,而是使用了指数加权平均。关于指数加权平均的意义,大家可参考这篇文章
《指数加权平均_LiuHDme的博客-CSDN博客_指数加权平均》
2.8 负向年化收益波动率(LPM)计算
# 负向收益波动率(年化)LPM
def Calc_LPM(fundRet):
'''
Parameters
----------
fundRet : 基金收益率.
Returns
-------
LPM : 负向收益年化波动率.
'''
fundRet = fundRet[fundRet<0]
LPM = fundRet.std()*np.sqrt(250)#将日标准差转化为年化标准差
return LPM
年化波动率:代码中并未直接使用收益率的日波动率,而是将日波动率转化为了年化波动率。
2.9 年化收益波动率(SIGMA)计算
# 收益波动率(年化)SIGMA
def Calc_SIGMA(fundRet):
'''
Parameters
----------
fundRet : 基金收益率.
Returns
-------
收益年化波动率.
'''
return fundRet.std()*np.sqrt(250)#将日波动率转化为年化波动率
2.10 自定义函数整合
# 基础指标计算合并
def AutoCalculate(fundRet,indexRet,netvalue,level):
'''
Parameters
----------
fundRet : 基金收益率.
indexRet : 指数收益率.
netvalue : 基金净值.
level : 置信水平.
Returns
-------
ret : 基金的收益指标和风险指标.
'''
ret = {}
HR = annual_yield(fundRet)
Alpha = Calc_Alpha(fundRet,indexRet)
MVaR = Calc_MVaR(fundRet,level)
MD = Calc_MD(netvalue)
AD = Calc_AD(netvalue)
LPM = Calc_LPM(fundRet)
SIGMA = Calc_SIGMA(fundRet)
#由于风险类指标越小,基金表现越优,所以要转换成其倒数,变成正向关系
dMVaR=np.exp( MVaR*-1.0)#应该也可以直接取倒数
dMD=np.exp( MD*-1.0)
dAD=np.exp( AD*-1.0)
dLPM=np.exp(LPM*-1.0)
dSIGMA=np.exp(SIGMA*-1.0)
ret.update({'HR':HR,'Alpha':Alpha,'dMVaR':dMVaR,'dMD':dMD,'dAD':dAD,'dLPM':dLPM,'dSIGMA':dSIGMA})
H_Mvar = HR/(np.exp(MVaR))#应该也可以直接除以MVaR,两者的差异暂未研究
CR = HR/np.abs(MD)
H_Ad = HR/np.abs(AD)
SoR = HR/LPM
SR = HR/SIGMA
A_Mvar = Alpha/(np.exp(MVaR))
A_Md = Alpha/np.abs(MD)
A_Ad = Alpha/np.abs(AD)
XR = Alpha/LPM
IR = Alpha/SIGMA
ret.update({'H_Mvar': H_Mvar,'CR':CR,'H_Ad':H_Ad,'SoR':SoR,'SR':SR,'A_Mvar':A_Mvar,'A_Md':A_Md,'A_Ad':A_Ad,'XR':XR,'IR':IR})
return ret
2.11计算混合基金指数(业绩比较基准)
# 计算混合型基金指数,为计算indexret做准备
def Calc_FundIndex(data):
datelist = list(pd.Series(list(set(list(data['endDate'])))).sort_values())#筛选出时间列表,并升序排列
IndexValue = {}
for date in datelist:
temp = data[data['endDate']==date]
IndexValue.update({date:temp['ADJUST_NAV'].mean()}) # 等权合成基金指数
IndexValue = pd.Series(IndexValue)
IndexValue = IndexValue/IndexValue.iloc[0]#基金指数的初始值,初始化为1
return IndexValue
2.12计算指数收益率
#计算混合型基金指数收益率
def Calc_IndexReturns(IndexData):
ret = (IndexData-IndexData.shift(1))/IndexData.shift(1)#计算收益率
ret = ret.dropna()#删除空值
return ret
2.13计算基金的各指标数值
#计算各指标,并保存为pd.dataframe
returns_H = Calc_Returns(fund_id,fund_data)
Indextype_H = Calc_FundIndex(fund_data) # 混合型基金指数
returns_Index_H = Calc_IndexReturns(Indextype_H)#计算基金指数收益率
ret = {}
for fund in fund_id:
try:
fundRet = returns_H[fund]
temp = fund_data[fund_data['secID']==fund]
temp = temp.set_index('endDate')
netvalue = temp['ADJUST_NAV']
calc = AutoCalculate(fundRet,returns_Index_H,netvalue,0.05) # 计算各指标
ret.update({fund:calc})
except: # 如果可观测的数据不够
pass
ret = pd.DataFrame(ret) #转换成pd数据框
ret = ret.transpose() #转置,获取最终数据结果
3 主成分分析
3.1 数据标准化
#数据标准化
stdret=np.zeros((61,17))
stdret=pd.DataFrame(stdret)
for col in range(17):
stdret.iloc[:,col]=np.array((ret.iloc[:,col]-ret.iloc[:,col].mean())/ret.iloc[:,col].std())
目的:数据标准化一是为了消除量纲的影响。例如比较GDP总量和GDP增长率之间的关系,那GDP总量的方差均值都较大不利于比较。而是为了方便计算,零均值化之后,矩阵的相关系数和协方差矩阵将是一致的。
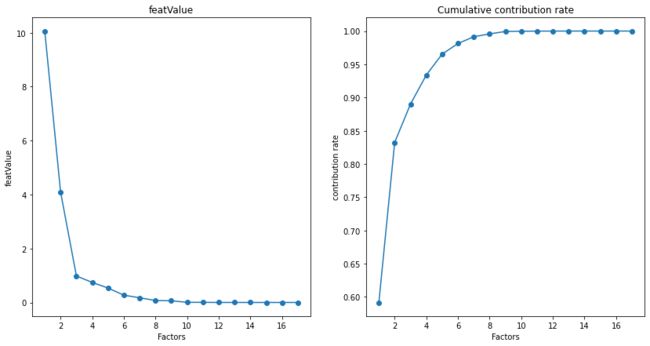
3.2 查看碎石土和累计贡献率
#计算协方差矩阵
cov_mat=np.cov(stdret.T)
#求解特征值和特征向量
featValue, featVec= np.linalg.eig(cov_mat)
#查看碎石土和累计贡献率
plt.figure(figsize=(14,7))
plt.subplot(121)#碎石土
plt.scatter(range(1, stdret.shape[1] + 1),featValue)
plt.plot(range(1, stdret.shape[1] + 1),featValue)
plt.title("featValue")
plt.xlabel("Factors")
plt.ylabel("featValue")
plt.subplot(122)#累计贡献率
gx = featValue/np.sum(featValue)
lg = np.cumsum(gx)#累加
plt.scatter(range(1, stdret.shape[1] + 1),lg)
plt.plot(range(1, stdret.shape[1] + 1),lg)
plt.title("Cumulative contribution rate")
plt.xlabel("Factors")
plt.ylabel("contribution rate")
plt.show()
左边为碎石土,右边为累计率。从累计贡献率来看当选取三个主成分时,累计贡献率就已经达到了85%以上,因此我们选择前三个主成分。
3.3 计算主成分得分
#计算主成分得分
selectVec = np.matrix(featVec[:3])
fscore = np.dot(selectVec,stdret.T).T#计算三个主成分得分
fscore = pd.DataFrame(fscore ,columns=["f1","f2","f3"],index=ret.index)
fscore["score"]=gx[0]*fscore["f1"]+gx[1]*fscore["f2"]+gx[2]*fscore["f3"]#根据方差贡献率进行加权,得出最终分数
fscore=fscore.sort_values(by="score", ascending=False)#进行降序排列
3.4 得分前五名和后五名的基金净值走势图
#前五名基金净值走势和后五名基金净值走势对比
plt.figure(figsize=(28,14))
top5_fundid=fscore.head().index
i=0
for top_id in top5_fundid:
i=i+1
plt.subplot(250+i)
plt.title(top_id)
temp=fund_data[fund_data["secID"]==top_id]['ADJUST_NAV']
plt.plot(temp)
tail5_fundid=fscore.tail().index
i=0
for tail_id in tail5_fundid:
i=i+1
plt.subplot(2,5,5+i)
plt.title(tail_id)
temp=fund_data[fund_data["secID"]==tail_id]['ADJUST_NAV']
plt.plot(temp)
plt.show()
第一行为得分前五名的基金业绩走势图,第二行为后五名的基金业绩走势图。(从走势来看,好像没有什么特别大的差异。)
参考资料:
[1]指数加权平均_LiuHDme的博客-CSDN博客_指数加权平均
[2]偏度(skewness)和峰度(kurtosis)_不论如何未来很美好的博客-CSDN博客_skewness和kurtosis
[3]基于主成分分析( PCA)的筛选基金策略 - 社区 - 优矿 (datayes.com)
- 本文章,首发于微信公众号:宏蜘蛛,原文链接:利用主成分分析(PCA)法对基金进行排名