从数据分布的角度提高对抗样本的可迁移性

1 引言

 对抗迁移性攻击一般是先通过代理模型生成对抗样本，然后将该样本迁移到其它黑盒模型中进行攻击，对抗迁移性的根本原因目前仍有待于探究。以前的工作主要从模型的角度探讨原因，例如决策边界、模型架构和模型容量等。在该论文中，作者从数据分布的角度研究对抗样本的可迁移性，其核心思想是针对于无目标攻击，将图像移出其原始分布会使不同的模型很难对图像进行正确分类。针对于有目标攻击，则是将图像拖入目标分布会误导模型将图像分类为目标类。因此作者提出了一种通过操纵图像的分布来生成对抗样本的新方法。实验结果证明了所提出方法的有效性。

论文链接：https://arxiv.org/abs/2210.04213
论文代码：https://github.com/alibaba/easyrobust

2 预备知识

 给定一个参数$\theta$的代理模型$f_{\theta }$，图像$\mathbf{x}$，标签$y$，其中共$n$类，$f_{\theta }(x)[k]$表示神经网络最后一层第$k$类输出，则条件概率$p_{\theta }(y|\mathbf{x})$表示为
$$p_{\theta }(y|\mathbf{x})=\frac{\exp (f_{\theta }(\mathbf{x})[y])}{\sum _{k=1}^n\exp (f_{\theta }(\mathbf{x})[k])}$$对抗扰动通常是损失函数$\mathcal{L}$关于样本$\mathbf{x}$的梯度，无目标攻击可以表示为：
$${\mathbf{x}}^{\prime }=\mathbf{x}+{\nabla }_{\mathbf{x}}\mathcal{L}(f_{\theta }(\mathbf{x}),y)=\mathbf{x}-{\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x})$$其中${\mathbf{x}}^{\prime }$是$\mathbf{x}$的对抗样本。有目标公式可以表示为$${\mathbf{x}}^{\prime }=\mathbf{x}-{\nabla }_{\mathbf{x}}\mathcal{L}(f_{\theta }(\mathbf{x}),y_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}})=\mathbf{x}+{\nabla }_{\mathbf{x}}\log p_{\theta }(y_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}|\mathbf{x})$$

3 论文方法

 在介绍论文方法之前，需要先对比一下在黑盒迁移攻击中作者的攻击策略与流行攻击策略的不同之处。如下图所示，一般流行的攻击策略先用数据集训练出一个普通的代理分类模型，然后在该代理模型中利用一个好的攻击算法去生成对抗样本，再将该对抗样本迁移到其它黑盒模型中进行攻击，该攻击策略的核心部分在于提出一个好的攻击算法。而论文中，作者的攻击策略是先训练出一个好的代理模型，该分类模型不仅可以正确分类样本，而且可以估计出数据分布关于样本的梯度，然后在该代理模型中利用一个普通攻击算法去生成对抗样本，再将该对抗样本迁移到其它黑盒模型中进行攻击，该攻击策略的核心部分在于提出一个多功能的代理模型分类器。

 作者从数据分布的视角下提出了一个可以理解和提高对抗样本可迁移性的算法，该算法建立在机器学习方法中的经典假设之上，深度学习模型可以正确分类与训练集独立同分布的验证集的数据，但很难对分布外的样本进行分类，即深度学习模型能够正确将与$p_D(\mathbf{x}|y)$独立同分布的数据分类预测为标签$y$，但是它不能处理该分布以外的数据。作者假设将图片移动到初始分布以外的区域即可实现迁移性高的无目标攻击，将图片移动到目标分布$p_D(\mathbf{x}|y_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}})$即可实现迁移性高的有目标攻击。即如下两图所示：


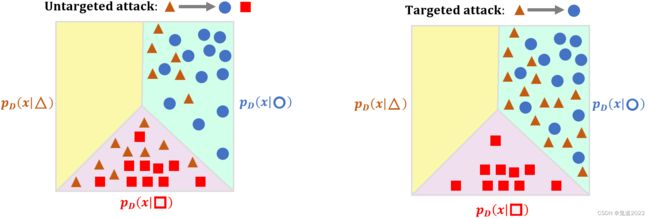
 作者借用score-matching生成模型的想法，其中该方法主要估计真实数据分布的梯度，然后通过SGLD的迭代公式将图像从初始分布$P_D(\mathbf{x}|y_0)$移动到目标分布$P_D(\mathbf{x}|y)$
$${\mathbf{x}}_t={\mathbf{x}}_{t-1}+\alpha \cdot {\nabla }_{{\mathbf{x}}_{t-1}}\log p_D({\mathbf{x}}_{t-1}|y)+\sqrt{2\alpha }\cdot ϵ$$其中$ϵ\sim \mathcal{N}(0,I)$，$\alpha$表示固定步长。当$\alpha \to 0$和$T\to \infty$时，${\mathbf{x}}_T$则精确地从分布$p_D(\mathbf{x}|y)$采样。

 作者定义了对数条件概率密度梯度和真实标签条件数据分布梯度的距离公式
$$\begin{array}{rl}\mathrm{D}\mathrm{C}\mathrm{G}& ={\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D(\mathbf{x}|y)}\Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x})-{\nabla }_{\mathbf{x}}\log p_D(\mathbf{x}|y){\Vert }_2^2\\ & =\int \int \Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x})-{\nabla }_{\mathbf{x}}\log p_D(\mathbf{x}|y){\Vert }_2^2{p}_D(\mathbf{x}|y)p_D(y)d\mathbf{x}dy\\ & =\int \int \Vert {\nabla }_{\mathbf{x}}\log p_D(\mathbf{x}|y){\Vert }_2^2{p}_D(\mathbf{x}|y)p_D(y)d\mathbf{x}dy\\ & +\int \int \Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}){\Vert }_2^2{p}_D(\mathbf{x}|y)p_D(y)d\mathbf{x}dy\\ & -2\int \int ({\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}{)}^{\top }\cdot {\nabla }_{\mathbf{x}}\log p_D(\mathbf{x}|y))p_D(\mathbf{x}|y)p_D(y)d\mathbf{x}dy\end{array}$$第一项与参数$\theta$无关可以忽略；中间项比较难求因为真实分布不可知；最后一项不能够直接计算，因为${\nabla }_{\mathbf{x}}\log p_D(\mathbf{x}|y)$是不可知的。利用部分积分法可以对以上公式进行简化，具体推导如下所示$$\begin{array}{rl}& {\int }_{-\infty }^{+\infty }{p}_D(y){\int }_{\mathbf{x}\in {\mathbb{R}}^n}({\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}{)}^{\top }\cdot {\nabla }_{\mathbf{x}}\log p_D(\mathbf{x}|y))p_D(\mathbf{x}|y)d\mathbf{x}dy\\ =& {\int }_{-\infty }^{+\infty }{p}_D(y){\int }_{\mathbf{x}\in {\mathbb{R}}^n}({\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}{)}^{\top }\cdot {\nabla }_{\mathbf{x}}{p}_D(\mathbf{x}|y))d\mathbf{x}dy\\ =& {\int }_{-\infty }^{+\infty }{p}_D(y)\sum _{i=1}^n{\int }_{\mathbf{x}\in {\mathbb{R}}^n}{\nabla }_{x_i}\log p_{\theta }(y|\mathbf{x}){\nabla }_{x_i}{p}_D(\mathbf{x}|y)d\mathbf{x}dy\\ =& {\int }_{-\infty }^{+\infty }{p}_D(y)\sum _{i=1}^n{\int }_{{\tilde{\mathbf{x}}}_i\in {\mathbb{R}}^{n-1}}\left[{\int }_{-\infty }^{+\infty }{\nabla }_{x_i}\log p_{\theta }(y|\mathbf{x}){\nabla }_{x_i}{p}_D(\mathbf{x}|y)d{x}_i\right]d{\tilde{\mathbf{x}}}_{i}dy\\ =& {\int }_{-\infty }^{+\infty }{p}_D(y)\sum _{i=1}^n{\int }_{{\tilde{\mathbf{x}}}_i\in {\mathbb{R}}^{n-1}}\left[\underset{M\to \infty }{\lim }{p}_D(\mathbf{x}|y){\nabla }_{{\mathbf{x}}_i}\log p_{\theta }(y|\mathbf{x}){|}_{-M_i}^{+M_i}\right]d{\tilde{\mathbf{x}}}_{i}dy\\ -& {\int }_{-\infty }^{+\infty }{p}_D(y)\sum _{i=1}^n{\int }_{{\tilde{\mathbf{x}}}_i\in {\mathbb{R}}^{n-1}}\left[{\int }_{-\infty }^{+\infty }{p}_D(\mathbf{x}|y){\nabla }_{x_i}^2\log p_{\theta }(y|\mathbf{x})d{x}_i\right]d{\tilde{\mathbf{x}}}_{i}dy\\ =& {\int }_{-\infty }^{+\infty }{p}_D(y)\sum _{i=1}^n{\int }_{{\tilde{\mathbf{x}}}_i\in {\mathbb{R}}^{n-1}}\left[\underset{M\to \infty }{\lim }{p}_D(\mathbf{x}|y){\nabla }_{x_i}\log p_{\theta }(y|\mathbf{x}){|}_{-M_i}^{+M_i}\right]d{\tilde{\mathbf{x}}}_i\\ -& {\int }_{-\infty }^{+\infty }{p}_D(y)\sum _{i=1}^n{\int }_{\mathbf{x}\in {\mathbb{R}}^n}\left[p_D(\mathbf{x}|y){\nabla }_{x_i}^2\log p_{\theta }(y|\mathbf{x})\right]d\mathbf{x}dy\\ =& {\int }_{-\infty }^{\infty }{p}_D(y)dy\sum _{i=1}^n{\int }_{\tilde{\mathbf{x}}\in {\mathbb{R}}^{n-1}}\left[\underset{M\to \infty }{\lim }{p}_D(\mathbf{x}|y){\nabla }_{x_i}\log p_{\theta }(y|\mathbf{x}){|}_{-M_i}^{+M_i}\right]d{\tilde{\mathbf{x}}}_{i}dy\\ -& {\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D(\mathbf{x}|y)}\left[\mathrm{t}\mathrm{r}({\nabla }_{\mathbf{x}}^2\log p_{\theta }(y|\mathbf{x}))\right]\\ =& -{\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D(\mathbf{x}|y)}\left[\mathrm{t}\mathrm{r}({\nabla }_{\mathbf{x}}^2\log p_{\theta }(y|\mathbf{x}))\right]\end{array}$$其中${\nabla }_{\mathbf{x}}$表示关于$\mathbf{x}$的Hessian矩阵，$+M_i$表示向量$[x_1,\cdots ,x_{i-1},+M,x_{i+1},\cdots ,x_n]$；$-M_i$表示向量$[x_1,\cdots ,x_{i-1},-M,x_{i+1},\cdots ,x_n]$。$\mathbf{x}=[x_1,\cdots ,x_n]$表示$n$维向量。${\tilde{x}}_i=[x_1,\cdots ,x_{i-1},x_{i+1},\cdots ,x_n]$。因为当$\Vert \mathbf{x}{\Vert }_2\to \infty$时，概率分布$p_D(\mathbf{x}|y)\to 0$，进而则有如下公式$${\int }_{-\infty }^{+\infty }{\nabla }_{x_i}f(\mathbf{x}){\nabla }_{x_i}g(\mathbf{x})d{x}_i=\underset{M\to \infty }{\lim }g(\mathbf{x}){\nabla }_{x_i}f(\mathbf{x}){|}_{-M_i}^{+M_i}-{\int }_{-\infty }^{+\infty }g(\mathbf{x}){\nabla }_{x_i}^{2}f(\mathbf{x})d{x}_i$$综上所述，DCG距离公式可以重新表示为$$\begin{array}{rl}\mathrm{D}\mathrm{C}\mathrm{G}& ={\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D(\mathbf{x}|y)}\Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x})-{\nabla }_{\mathbf{x}}\log p_D(\mathbf{x}|y){\Vert }_2^2\\ & ={\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D}(\mathbf{x}|y)\Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}){\Vert }_2^2+2{\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D(\mathbf{x}|y)}\left[\mathrm{t}\mathrm{r}({\nabla }_{\mathbf{x}}^2\log p_{\theta }(y|\mathbf{x}))\right]+\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\end{array}$$忽略常数项，进而则有$${\mathcal{L}}_{\mathrm{D}\mathrm{C}\mathrm{G}}={\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D}(\mathbf{x}|y)\Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}){\Vert }_2^2+2{\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D(\mathbf{x}|y)}\left[\mathrm{t}\mathrm{r}({\nabla }_{\mathbf{x}}^2\log p_{\theta }(y|\mathbf{x}))\right]$$以上公式涉及到求解Hessian矩阵的迹，当矩阵的维度很高时，计算量也会飙升。当给定任意方阵$\mathbf{A}$，可以采用一种随机算法去估计矩阵的迹$\mathrm{t}\mathrm{r}(\mathbf{A})$，给定一个随机向量$\mathbf{v}$且有${\mathbb{E}}_{p(\mathbf{v})}\left[\mathbf{v}{\mathbf{v}}^{\top }\right]=I$，进而则有$\mathrm{t}\mathrm{r}(\mathbf{A})={\mathbb{E}}_{p(\mathbf{v})}\left[{\mathbf{v}}^{\top }\mathbf{A}\mathbf{v}\right]$。所以可以用${\mathbb{E}}_{p(\mathbf{v})}\left[{\mathbf{v}}^{\top }{\nabla }_{\mathbf{x}}^2\log p_{\theta }(y|\mathbf{x})\mathbf{v}\right]$代替矩阵的迹$\mathrm{t}\mathrm{r}({\nabla }_{\mathbf{x}}^2\log p_{\theta }p(y|\mathbf{x}))$，所以损失函数$\mathrm{D}\mathrm{C}\mathrm{G}$可以表示为$${\mathcal{L}}_{\mathrm{D}\mathrm{C}\mathrm{G}}={\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D}(\mathbf{x}|y)\Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}){\Vert }_2^2+2{\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D(\mathbf{x}|y)}{\mathbb{E}}_{p(\mathbf{v})}\left[{\mathbf{v}}^{\top }{\nabla }_{\mathbf{x}}^2\log p_{\theta }(y|\mathbf{x})\mathbf{v}\right]$$作者首先通过用交叉熵损失和DCG损失联合训练出一个代理模型，优化目标如下所示$$\underset{\theta }{\min }\left[\mathcal{L}(f_{\theta }(x),y)+\lambda {\mathcal{L}}_{\mathrm{D}\mathrm{C}\mathrm{G}}\right]$$其中$\lambda$表示正则化系数。模型训练结束后可以得到如下图所示的梯度分布，其中可以发现梯度是从样本点稀疏的区域流向样本点密集的区域，而且样本点稀疏的区域梯度值更大，样本点密集区梯度值更小。

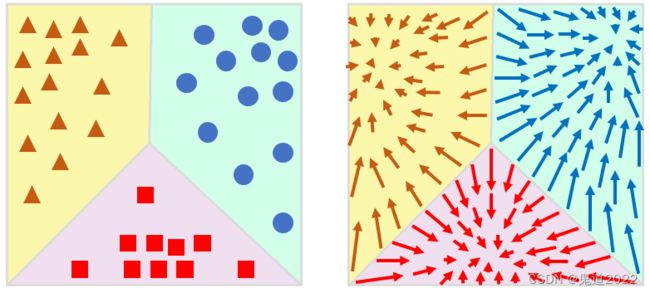
之后再用该代理模型生成对抗样本，无目标攻击的形式如下所示$$\{\begin{array}{rl}{\mathbf{x}}_n& ={\mathbf{x}}_{n-1}+\eta \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}({\nabla }_{{\mathbf{x}}_{n-1}}\mathcal{L}(f_{\theta }({\mathbf{x}}_{n-1}),y_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{l}})\\ {\mathbf{x}}_n& =\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}({\mathbf{x}}_n,{\mathbf{x}}_0-ϵ,{\mathbf{x}}_0+ϵ)\end{array}$$有目标攻击的形式表示为$$\{\begin{array}{rl}{\mathbf{x}}_n& ={\mathbf{x}}_{n-1}-\eta \cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}({\nabla }_{{\mathbf{x}}_{n-1}}\mathcal{L}(f_{\theta }({\mathbf{x}}_{n-1}),y_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}})\\ {\mathbf{x}}_n& =\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}({\mathbf{x}}_n,{\mathbf{x}}_0-ϵ,{\mathbf{x}}_0+ϵ)\end{array}$$综上所述可以发现，之前对抗迁移性的工作都是基于优化的方法，而本文作者则是关注点放在真实数据分布上，首先将真实数据分布关于样本的梯度与代理模型分布关于样本的梯度相匹配。然后在训练好的代理模型上生成对抗样本，具体过程如下图所示。

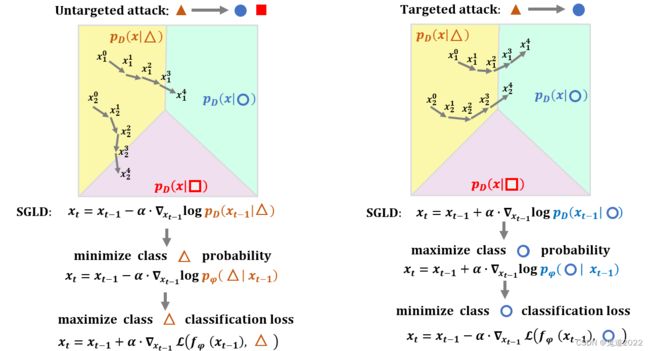
实验结果

 该论文的实验结果非常出色，如下图所示为在黑盒迁移攻击下，不同的攻击算法的无目标攻击的攻击成功率。可以惊奇的发现论文中提出的方法的攻击成功率比其它攻击算法要高出一个等级，甚至在某些模型中如VGG19，RN152，DN121和DN201模型，其黑盒迁移攻击成功率要直逼白盒攻击成功率。

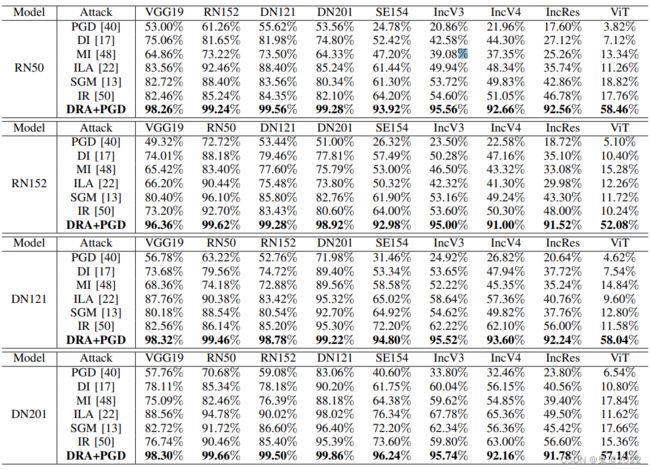
 下图是论文的一个定性的结果，可以清晰的发现，当源类目标为青蛙，目标攻击类为玉米的时候，可以发现论文中提出的攻击方法生成的对抗样本在青蛙的腿上有清晰的玉米特征。

代码实现

 论文的代码已开源，为了能够更好的理解论文方法，以下程序是根据论文的算法流程图编写的一个在mnist数据集上的一个简易的程序。论文中的损失函数变成起来较为棘手，原始的损失函数如下所示$${\mathcal{L}}_{\mathrm{D}\mathrm{C}\mathrm{G}}={\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D}(\mathbf{x}|y)\Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}){\Vert }_2^2+2{\mathbb{E}}_{p_D(y)}{\mathbb{E}}_{p_D(\mathbf{x}|y)}{\mathbb{E}}_{p(\mathbf{v})}\left[{\mathbf{v}}^{\top }{\nabla }_{\mathbf{x}}^2\log p_{\theta }(y|\mathbf{x})\mathbf{v}\right]$$需要对该损失函数的形式进行一定的变换，变换形式如下所示：$${\mathcal{L}}_{\mathrm{D}\mathrm{C}\mathrm{G}}={\mathbb{E}}_{p_D(x,y)}\Vert {\nabla }_{\mathbf{x}}\log p_{\theta }(y|\mathbf{x}){\Vert }_2^2+2{\mathbb{E}}_{p_D(x,y)}{\mathbb{E}}_{p(\mathbf{v})}\left[{\mathbf{v}}^{\top }{\nabla }_{\mathbf{x}}^2\log p_{\theta }(y|\mathbf{x})\mathbf{v}\right]$$进一步可得其离散的形式为，根据离散形式的损失函数，可以更好地对论文算法进行实现。$${\mathcal{L}}_{\mathrm{D}\mathrm{C}\mathrm{G}}=\frac{1}{N}\sum _{i=1}^N\Vert {\nabla }_{{\mathbf{x}}_i}\log p_{\theta }(y_i|{\mathbf{x}}_i){\Vert }_2^2+\frac{2}{MN}\sum _{i=1}^N\sum _{j=1}^M\left[{\mathbf{v}}_j^{\top }{\nabla }_{{\mathbf{x}}_i}^2\log p_{\theta }(y_i|{\mathbf{x}}_i){\mathbf{v}}_j\right]$$

from torchvision import datasets, transforms
from torch.utils.data import DataLoader, Dataset
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.optim as optim
import torch.nn.functional as F
import os

        
class Net(nn.Module):
	def __init__(self):
		super(Net, self).__init__()
		self.fc1 = nn.Linear(784, 300)
		self.fc2 = nn.Linear(300, 100)
		self.fc3 = nn.Linear(100, 10)
	def forward(self, x):
		x = F.relu(self.fc1(x))
		x = F.relu(self.fc2(x))
		out = self.fc3(x)
		return out

def DR_training():
	lambda1 = 0
	lambda2 = 1
	epoch = 5
	model = Net()
	optimizer = torch.optim.SGD(model.parameters(), lr=0.005)
	loss_fn = torch.nn.CrossEntropyLoss()
	use_cuda = torch.cuda.is_available()

	mnist_transform = transforms.Compose([transforms.ToTensor(), transforms.Lambda(lambda x : x.resize_(28*28))])
	mnist_train = datasets.MNIST(root="mnist-data", train=True, download=True, transform=mnist_transform)
	train_loader = torch.utils.data.DataLoader(mnist_train, batch_size=32, shuffle=True, num_workers=0)

	for epoch_idx in range(epoch):
		for batch_idx, (inputs, targets) in enumerate(train_loader):
			if use_cuda:
				inputs, targets = inputs.cuda(), targets.cuda()
			inputs, targets = Variable(inputs), Variable(targets)

			inputs.requires_grad_(True)

			predict = model(inputs)

			CE_loss = loss_fn(predict, targets)

			# DCG loss

			# Grad loss
			log_pro = torch.log(F.softmax(predict, 1))
			log_pro_target = log_pro.gather(1, targets.view(-1,1)).squeeze(1)
			grad = torch.autograd.grad(log_pro_target, inputs, grad_outputs = torch.ones_like(log_pro_target), retain_graph = True, create_graph=True)
			DCG_grad_loss = torch.mean(torch.norm(grad[0], dim = 1, p = 2))


			# Hessian loss
			v = torch.rand_like(inputs)
			v = v / torch.norm(v, dim = -1, keepdim = True)

			mid_vector = torch.sum(v * grad[0], dim = 1)

			grad2 = torch.autograd.grad(mid_vector, inputs, grad_outputs = torch.ones_like(mid_vector), retain_graph = True, create_graph = True)

			DCG_Hessian_loss = torch.mean(torch.sum(v * grad2[0], dim = 1))


			DCG_loss = DCG_grad_loss + 2 * DCG_Hessian_loss


			loss = lambda1 * CE_loss + lambda2 * DCG_loss

			print('CE_loss: ', CE_loss.item(), 'grad_loss: ',  DCG_grad_loss.item(), 'Hessian_loss: ', DCG_Hessian_loss.item(), 'loss: ',loss.item)

			optimizer.zero_grad()
			loss.backward()
			optimizer.step()

			print('successful')



if __name__ == '__main__':
	DR_training()