【点云处理之狂读论文经典篇1】——3D ShapeNets: A Deep Representation for Volumetric Shapes

1.摘要

1. 提出了一种将几何3D形状表示为3D体素网格中的二值变量概率分布方法，然后用卷积深度网络进行处理。
2. 不仅可以对3D形状进行操作，2.5D的深度图也可以处理，可以使用单视图的方法，也可以使用Next-Best-View 优化识别率。
3. 构造了ModelNet，一个规模很大的CAD模型3D数据集，用于3D深度训练。

2.引言

1. 本文探寻一种能够用于目标识别和形状补全的通用3D形状表示方法。
2. 当类别识别的第一个视角不充分时，识别系统还需要找到更优的观察视角。

3.相关工作

1. Assembly-based approach
2. Smooth interpolation-based approach
3. Template-based approach
4. Deep learning-based approach
5. Next-Best-View problem

4.3D ShapeNets

3D voxel grid的构建可以参考此篇Blog。

Convolutional Deep Belief Network (CDBN)的构建具有以下特点：

1. 通过卷积权值共享的方法减少模型参数。
2. 不使用任何的池化操作（因为在形状重建的时候会导致很大的不确定性）。

3D shapeNet的整体架构

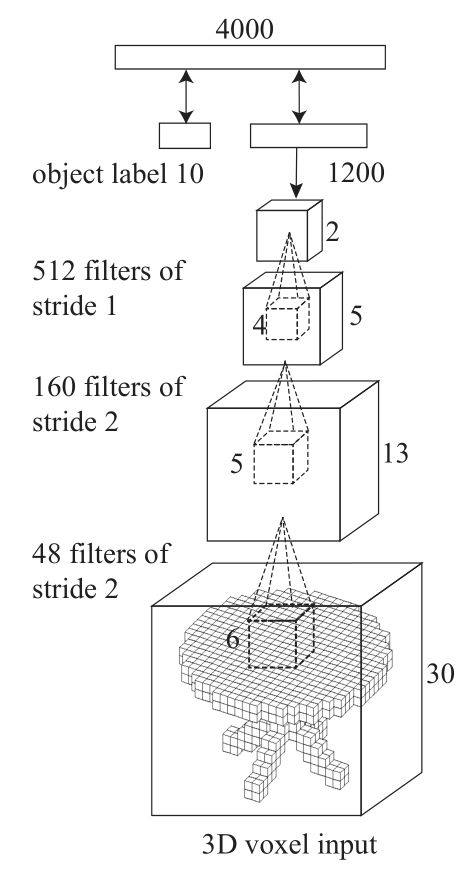
Convolutional Deep Belief Network (CDBN)的构建配置：

1. 网格大小为30×30×30，在表示形状的时候，要在上下左右空出3个多余的格子，减少卷积边界的误差，所以目标形状的范围是24×24×24。
2. 第一层：使用48个大小为6的卷积核，步数为2。
3. 第二层：使用160个大小为5的卷积核，步数为2.
4. 第三层使用512个大小为4的卷积核。
5. 第四层：全连接，有1200个隐藏单元。
6. 第五层：全连接，有4000个隐藏单元，输入为multinomial label variables和Bernoulli feature variables（不清楚说的是啥，看图是输入标签和第四层特征）
7. 训练的时候采用一层一层的预训练模式，前四层的训练方式为standard Contrastive Divergence，后两层的训练方式为Fast Persistent Contrastive Divergence(FPCD)。
8. 微调阶段使用wake sleep algorithm。第一层只学习感知域中非空的信号，还使用了sparsity regularization 。最后，we duplicate the label units 10 times to increase their significance.（不懂，有知道的小伙伴可以在评论区讨论一下）

4. 2.5D Recognition and Reconstruction

4.1 View-based Sampling

在训练完CDBN后，模型学习到了体素数据$\mathbf{x}$和目标类别$y\in \{1,\cdots ,K\}$的联合分布函数$p(\mathbf{x},y)$。尽管模型是在3D形状上训练的，但是能够识别2.5D的深度图。

View-based 2.5D Object Recognition. (1) 解释如何从3D真实世界的物体拍摄深度图。(2) 展示了从椅子后面拍摄到的深度图，切面用于可视化。(3) 展示了切面的轮廓和不同类型的体素，椅子表面的体素是红色的，遮挡住的体素是蓝色的。(4) 展示了识别和形状补全的结果。

将2.5D深度图转换为体素表示，分成free、surface和occluded三个部分。free和surface被认为是可见的${\mathbf{x}}_o$，occluded是不可见的${\mathbf{x}}_u$，整体表示为$\mathbf{x}=({\mathbf{x}}_o,{\mathbf{x}}_u)$。

识别物体类别的任务可以表示为$p(y|{\mathbf{x}}_o)$，通过Gibbs sampling进行求解，具体可以参考此篇Blog。步骤如下：

1. 将${\mathbf{x}}_u$初始化为随机值，并将数据样$\mathbf{x}=({\mathbf{x}}_o,{\mathbf{x}}_u)$自底向上传播，以从$p(y|({\mathbf{x}}_o,{\mathbf{x}}_u))$中获取标签$y$的样本。
2. 然后，High level signal向下传播到体素$\mathbf{x}$的采样。
3. 对$\mathbf{x}$中可见的体素${\mathbf{x}}_o$进行截断，再进行自底向上的传播。

50次上下采样迭代应足以获得补全后的形状$\mathbf{x}$，以及对应的值$y$。上述步骤可以并行运行，从而产生与潜在不同类别相对应的各种补全结果。最后一个类别标签对应于采样频率最高的类别。

4.2 Next-Best-View Prediction

只从一个角度进行目标识别不太稳定，会识别出其他的类型，如果能够给定当前视角，模型能够预测下一个视角将会对鉴别目标类别产生巨大作用。

输入：

1. 未知目标的单副可见体素${\mathbf{x}}_o$
2. 有限个下一个视角的可选列表$\{{\mathbf{V}}^i\}$(相机的旋转和平移)

输出：

1. 从列表中选出最优的视图减少识别不稳定性

原始识别不确定度$H$由$y$的熵给出，该熵以观测到的${\mathbf{x}}_o$为条件：

$$\begin{array}{rl}H& =H\left(p\left(y\mid {\mathbf{x}}_o=x_o\right)\right)\\ & =-\sum _{k=1}^{K}p\left(y=k\mid {\mathbf{x}}_o=x_o\right)\log p\left(y=k\mid {\mathbf{x}}_o=x_o\right)\end{array}$$
其中，条件概率$p(y\mid {\mathbf{x}}_o=x_o)$可以通过从$p(y,{\mathbf{x}}_u\mid {\mathbf{x}}_o=x_o)$中取样并将${\mathbf{x}}_u$边缘化来近似。

当照相机被移动到另一个视图$\{{\mathbf{V}}^i\}$时，就会有一些以前未被观察到的体素 ${\mathbf{x}}_u$就会根据它的实际形状被观察到。不同的视图$\{{\mathbf{V}}^i\}$将导致这些未观察到的体素${\mathbf{x}}_u$的可见性不同。

Next-Best-View 预测. [行1，列1]：从单个视角得到的可见体素（红色）和未知体素（蓝色）。[行 2-4，列1]： 在(x_o, x_u)条件下生成的三种可能的补全样本。[行1， 列2-4]：三个可能的相机位置。[行2-4，列2-4]：在给定可能的形状和相机位置下，得到新的可视化目标图案。

在上图中，以$({\mathbf{x}}_o,{\mathbf{x}}_u)$为条件，可以采样出很多可能的形状，然后根据每一种假设可以获得$\{{\mathbf{V}}^i\}$视角下的深度图。通过这种方式，我们可以仿真出不同样本在不同视角下新的深度图。

令${\mathbf{x}}_n^i=\mathrm{Render}\left({\mathbf{x}}_u,{\mathbf{x}}_o,{\mathbf{V}}^i\right)\backslash {\mathbf{x}}_o$表示下一个视角下的新的可见体素，${\mathbf{x}}_n^i\subseteq {\mathbf{x}}_u$，是未知变量，将在以下等式中被边缘化。不确定度表示为：
$$\begin{array}{rl}{H}_i& =H\left(p\left(y\mid {\mathbf{x}}_n^i,{\mathbf{x}}_o=x_o\right)\right)\\ & =\sum _{{\mathbf{x}}_n^i}p\left({\mathbf{x}}_n^i\mid {\mathbf{x}}_o=x_o\right)H\left(y\mid {\mathbf{x}}_n^i,{\mathbf{x}}_o=x_o\right)\end{array}$$

上式中的条件熵可以通过下述步骤计算：

1. 从$p({\mathbf{x}}_u|{\mathbf{x}}_o=x_o)$中采样出足够的${\mathbf{x}}_u$
2. 做3D rendering，得到深度图，从${\mathbf{x}}_u$中得到${\mathbf{x}}_n^i$
3. 利用${\mathbf{x}}_n^i$计算$H\left(p\left(y\mid {\mathbf{x}}_n^i=x_n^i,{\mathbf{x}}_o=x_o\right)\right)$

根据信息论，$H-H_i=I\left(y;{\mathbf{x}}_n^i\mid {\mathbf{x}}_o=x_o\right)\ge 0$是以${\mathbf{x}}_o$为条件，$y$和${\mathbf{x}}_n^i$之间的相互信息。

因此，视角优化算法便是最大化这个相互信息：
$${\mathbf{V}}^{\ast }=\arg \underset{{\mathbf{V}}^i}{\max }I\left(y;{\mathbf{x}}_n^i\mid {\mathbf{x}}_o=x_o\right)$$

5.ModelNet: A Large-scale 3D CAD Dataset

数据来源：

1. 3D Warehouse
2. 3D模型搜索引擎 Yobi3D
3. SUN database
4. Princeton Shape Benchmark
5. 打标签工具 Amazon Mechanical Turk

共有660类，151128个3D模型。

6.实验

ModelNet40：40类，每类100个模型
ModelNet10：10类

每个模型沿着重力方向旋转12次（一次30°）
——应对旋转不变性

共有48000 CAD 训练

one Intel XEON E5-2690 CPU
one NVIDIA K40c GPU
训练了两天

6.1Classification and Retrieval

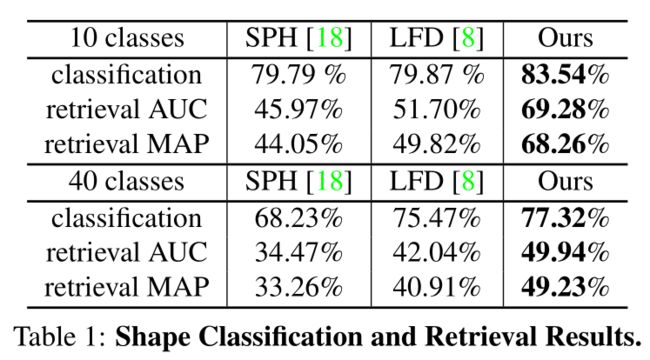
Classification，将第五层看作特征，再加一层线性SVM作为输出层，取每一类的平均值，对比的算法包括Light Field descriptor (LFD, 4,700 dimensions)、Spherical Harmonic descriptor (SPH, 544 dimensions)。

Retrieval，L2 distance被用于两种模型间的相似性。评价指标为recision-recall curve (AUC) 和mean average precision (MAP)。

38,400模型进行训练，9600个模型用于测试。

6.2 View-based 2.5D Recognition

NYU RGB-D dataset：10类， 4899个模型

先直接把在ModelNet上训练好的模型用在NYU数据集上

然后再微调

6.2Next-Best-View Prediction

主要看形状重建的性能$p\left({\mathbf{x}}_u\mid {\mathbf{x}}_o=x_o\right)$。

按理说，一个好的视图选择方案应该可以产生更高的识别精度。

7.总结

所提出的模型既可以识别，又能重建。