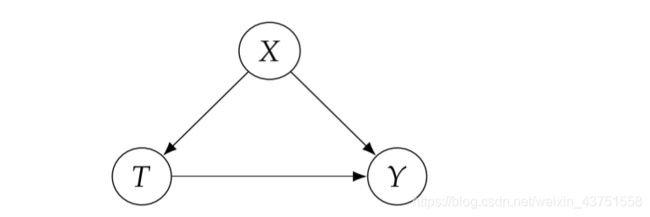
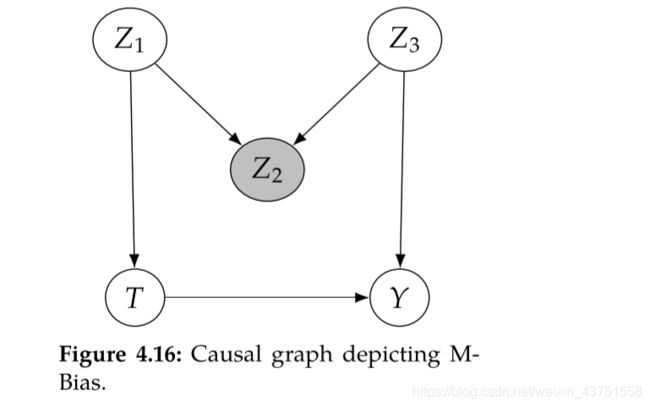
因果推理(四):因果模型
因果模型对于因果量的确定是很重要的。在前面的学习中,我们将“确定”(identification)描述为将因果估计转换为统计估计的过程。确定-估计(Identification-Estimation)的流程如下图:
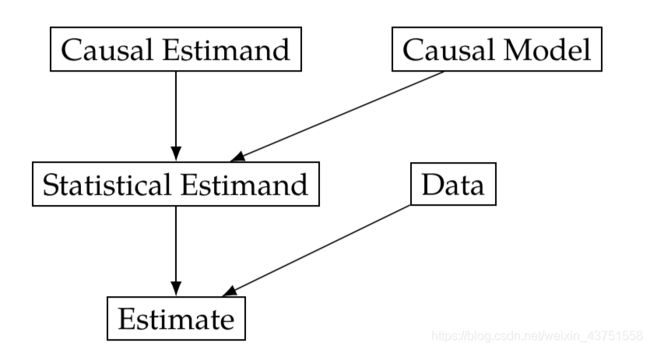
1. Do-算子和干预(interventional)分布
首先需要区别给定条件(condition)和干预(intervention)的概念。给定条件T=t的意思是我们只看在总体中treatment为t的子集;而intervention的意思是将总体中左右个体的treatment设为t。我们用do-算子表示intervention: d o ( T = t ) do(T=t) do(T=t)。这是图形因果模型中常用的表示法,并且在潜在结果表示法中具有相同的表示法。例如,可以将第二讲中的潜在结果表示为:
P ( Y ( t ) = y ) = P ( Y = y ∣ d o ( T = t ) ) = P ( y ∣ d o ( t ) ) P(Y(t)=y)=P(Y=y|do(T=t))=P(y|do(t)) P(Y(t)=y)=P(Y=y∣do(T=t))=P(y∣do(t))
在上式中将 d o ( T = t ) do(T=t) do(T=t)简写为 d o ( t ) do(t) do(t)。此外,全概率可表示为 Y ∣ d o ( t ) Y|do(t) Y∣do(t)。通常将 P ( Y ∣ d o ( T = t ) ) P(Y|do(T=t)) P(Y∣do(T=t))的形式叫做interventional distributions。
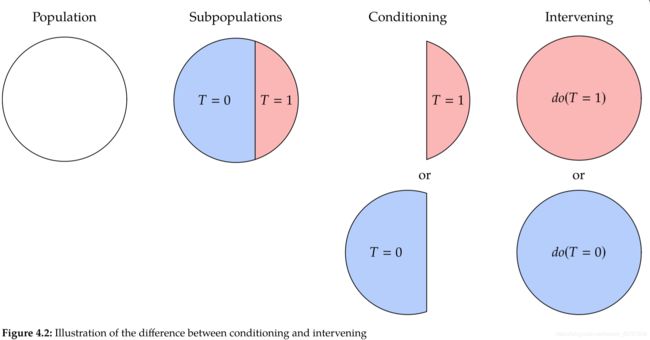
需要注意形如 P ( Y ∣ d o ( T = t ) ) P(Y|do(T=t)) P(Y∣do(T=t))的干预性分布(interventional distribution)和形如 P ( Y ) P(Y) P(Y)的观察分布(observational distribution)的区别。观察分布不带do算子,是不需要任何实验和干预就可以得到的变量分布。如果可以将带do算子的表达式(干预性表达式)转换为不带do算子的表达式(观察行表达式),就说这个表达式是可识别的(identifiable)。通常,将包含do算子的估计称为因果估计,将不包含do算子的估计称为统计估计。
带do算子的表达式中的所有变量都处于一个干预后的世界。(这里14节细讲)
2. 模块化假设(modularity)
在介绍模块化假设之前,需要先介绍因果机制(causal mechanism)的概念。可以将产生 X i X_i Xi的因果机制理解为给定 X i X_i Xi的所有原因的 X i X_i Xi的条件概率分布: P ( x i ∣ p a i ) P(x_i|pa_i) P(xi∣pai)。如下图所示,生成 X i X_i Xi的因果机制由 X i X_i Xi的所有父节点和指向 X i X_i Xi的所有边组成。
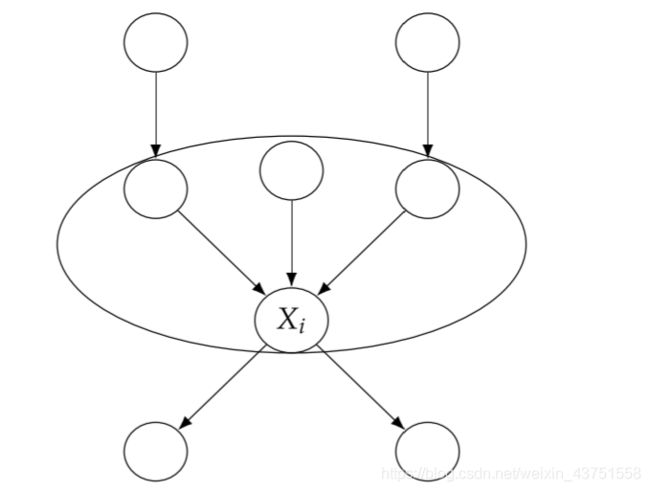
为了获得许多因果识别结果,我们将做出的主要假设是干预(iinterventions)是局部的。 更具体地说,我们假设对变量 X i X_i Xi的干预只会改变 X i X_i Xi的因果机制。 它不会改变产生任何其他变量的因果机制。 从这个意义上说,因果机制是模块化的。
模块化(modularity)假设:如果对节点集合 S ⊆ [ n ] S \subseteq[n] S⊆[n]进行干预,将它们设为常量,那么对于每一个i,有:
(1)如果 i ∉ S i \notin S i∈/S,那么 P ( x i ∣ p a i ) P\left(x_{i} \mid \mathrm{pa}_{i}\right) P(xi∣pai)保持不变。
(2)如果 i ∈ S i \in S i∈S,那么当 x i x_i xi为 X i X_i Xi被设为的值时 P ( x i ∣ p a i ) = 1 P\left(x_{i} \mid \mathrm{pa}_{i}\right)=1 P(xi∣pai)=1;否则, P ( x i ∣ p a i ) = 0 P\left(x_{i} \mid \mathrm{pa}_{i}\right)=0 P(xi∣pai)=0。
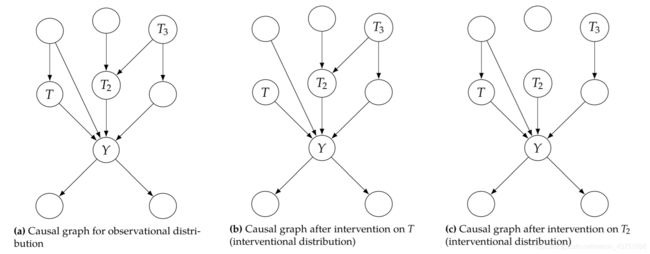
介入性分布的因果图(操纵图,manipulated graph)与观察性关节分布所使用的图完全相同,只是介入节点的所有边都被删除。这是因为干预因素的概率已设置为1,因此我们可以忽略该因素的所有因。
3. 截断式因式分解(Truncated Factorization)
回顾一下贝叶斯网络因式分解:
P ( x 1 , … , x n ) = ∏ i P ( x i ∣ p a i ) P\left(x_{1}, \ldots, x_{n}\right)=\prod_{i} P\left(x_{i} \mid \mathrm{pa}_{i}\right) P(x1,…,xn)=∏iP(xi∣pai)
现在,如果我们干预一组节点 S S S并假设其符合模块化(modularity),则除 X i ∈ S X_{i} \in S Xi∈S的因式外,所有因式都应保持相同;而 X i ∈ S X_{i} \in S Xi∈S的节点的因式变为1(值与干预一致时)。
截断式因式分解(Truncated Factorization):我们假设 P P P和 G G G满足马尔可夫假设和模块化。 给定一组干预节点 S S S,
如果 x x x与干预一致,则
P ( x 1 , … , x n ∣ d o ( S = s ) ) = ∏ i ∉ S P ( x i ∣ p a i ) P\left(x_{1}, \ldots, x_{n} \mid d o(S=s)\right)=\prod_{i \notin S} P\left(x_{i} \mid \mathrm{pa}_{i}\right) P(x1,…,xn∣do(S=s))=∏i∈/SP(xi∣pai).
否则, P ( x 1 , … , x n ∣ d o ( S = s ) ) = 0 P\left(x_{1}, \ldots, x_{n} \mid d o(S=s)\right)=0 P(x1,…,xn∣do(S=s))=0.
从贝叶斯网络因式分解变为上面的截断式分解的关键是,后者的乘积建立在 i ∉ S i \notin S i∈/S而不是全部的 i i i之上。 换句话说, i ∈ S i \in S i∈S的因子已被截断。
下面给出一个用截断因式分解计算因果量的例子。
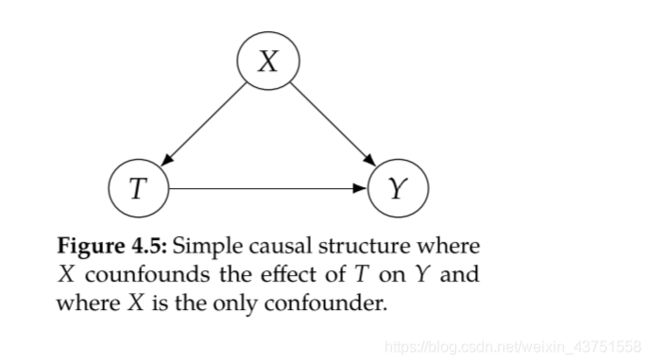
根据贝叶斯网络因式分解: P ( y , t , x ) = P ( x ) P ( t ∣ x ) P ( y ∣ t , x ) P(y, t, x)=P(x) P(t \mid x) P(y \mid t, x) P(y,t,x)=P(x)P(t∣x)P(y∣t,x)
根据截断因式分解: P ( y , x ∣ d o ( t ) ) = P ( x ) P ( y ∣ t , x ) P(y, x \mid d o(t))=P(x) P(y \mid t, x) P(y,x∣do(t))=P(x)P(y∣t,x)
边缘化X: P ( y ∣ d o ( t ) ) = ∑ x P ( y ∣ t , x ) P ( x ) P(y \mid d o(t))=\sum_{x} P(y \mid t, x) P(x) P(y∣do(t))=∑xP(y∣t,x)P(x)
4. 后门调整
回顾第3讲,因果关联从 T T T到 Y Y Y沿着有向路径流动,非因果关联沿着从 T T T到 Y Y Y的且满足以下约束的任何其他路径流动:1)非对撞节点在条件集中;2)对撞节点不在条件集中。 这些从 T T T到 Y Y Y的无方向无阻塞路径称为后门路径(backdoor paths)。 事实证明,如果我们可以通过调节条件来阻止这些后门路径,则可以确定形如的因果量 P ( Y ∣ d o ( t ) ) P(Y \mid d o(t)) P(Y∣do(t))。
后门标准(Backdoor Criterion):如果满足以下条件,则一组变量 W W W满足从 T T T到 Y Y Y的后门标准:
- W W W阻止从 T T T到 Y Y Y的所有后门路径。
- W W W不包含 T T T的任何后代。
满足后门准则使 W W W成为充分调整集(sufficient adjustment set)。
后门调整(Backdoor Adjustment):给定模块化假设,且W满足后门标准,则可以确定 T T T作用在 Y Y Y上的因果效应:
P ( y ∣ d o ( t ) ) = ∑ w P ( y ∣ t , w ) P ( w ) P(y \mid d o(t))=\sum_{w} P(y \mid t, w) P(w) P(y∣do(t))=∑wP(y∣t,w)P(w)
证明:
P ( y ∣ d o ( t ) ) = ∑ w P ( y ∣ d o ( t ) , w ) P ( w ∣ d o ( t ) ) = ∑ w P ( y ∣ t , w ) P ( w ∣ d o ( t ) ) = ∑ w P ( y ∣ t , w ) P ( w ) \begin{aligned} P(y \mid d o(t)) &=\sum_{w} P(y \mid d o(t), w) P(w \mid d o(t)) \\ &=\sum_{w} P(y \mid t, w) P(w \mid d o(t)) \\ &=\sum_{w} P(y \mid t, w) P(w) \end{aligned} P(y∣do(t))=w∑P(y∣do(t),w)P(w∣do(t))=w∑P(y∣t,w)P(w∣do(t))=w∑P(y∣t,w)P(w)
5. 结构因果模型(Structural Causal Models , SCMs)
结构方程
在因果模型中,用记号 : = := :=来表示因果关系,A是B的因可以记为: B : = f ( A ) B:=f(A) B:=f(A)或 B : = f ( A , U ) B:=f(A, U) B:=f(A,U),这样的式子被称为结构方程,其中 U U U是未被观测到的随机变量。
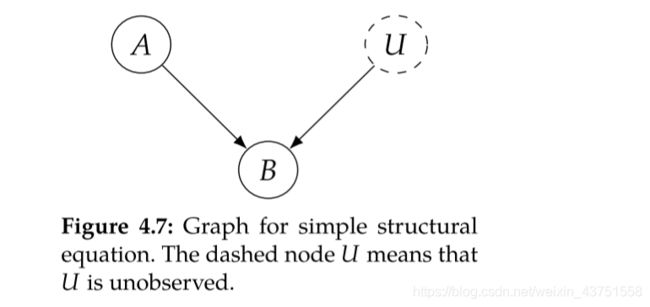
利用结构方程,我们可以对因果图进行建模。
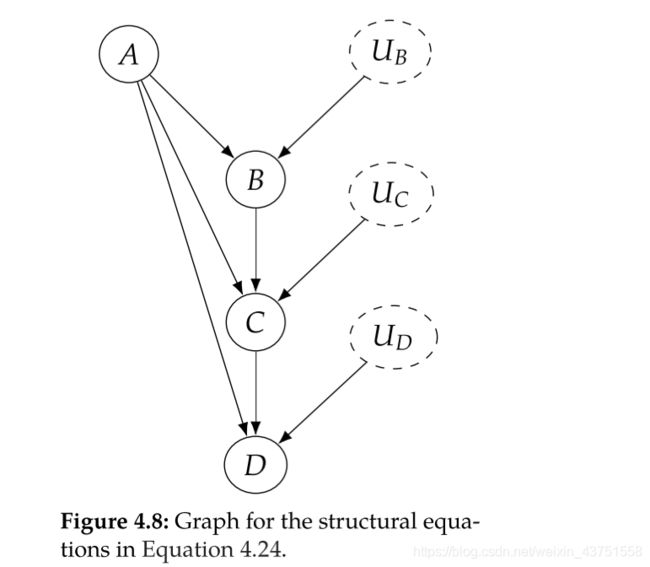
上图的因果图可以建模为M:
B : = f B ( A , U B ) C : = f C ( A , B , U C ) D : = f D ( A , C , U D ) \begin{aligned} B &:=f_{B}\left(A, U_{B}\right) \\ C &:=f_{C}\left(A, B, U_{C}\right) \\ D &:=f_{D}\left(A, C, U_{D}\right) \end{aligned} BCD:=fB(A,UB):=fC(A,B,UC):=fD(A,C,UD)
在因果图中,未被观测到的变量U通常不会显式画出。我们为之编写结构方程的变量称为内生(endogenous)变量。 这些是我们正在建模其因果机制的变量-在因果图中具有父节点的变量。 相反,外生(exogenous)变量是因果图中没有任何父节点的变量。例如,上图中的内生变量为 { B , C , D } \{B, C, D\} {B,C,D},外生变量为 { A , U B , U C , U D } \left\{A, U_{B}, U_{C}, U_{D}\right\} {A,UB,UC,UD}。
结构因果模型(Structural Causal Model , SCM)是以下集合的元组:
1)一组内生变量 V V V
2)一组外生变量 U U U
3)一组函数 f f f,其因变量为一个内生变量,自变量为其他变量。
干预(interventions)
在SCM中,如果干预 d o ( T = t ) do(T=t) do(T=t)表示为将T的结构方程改为 T : = t T:=t T:=t。例如,对于下列SCM M M M:
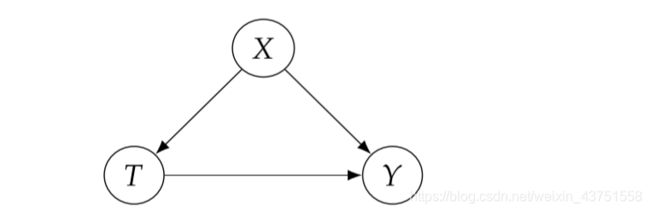
T : = f T ( X , U T ) T:=f_{T}\left(X, U_{T}\right) T:=fT(X,UT)
Y : = f Y ( X , T , U Y ) Y:=f_{Y}\left(X, T, U_{Y}\right) Y:=fY(X,T,UY)
对T进行干预后的模型为 M t M_t Mt:
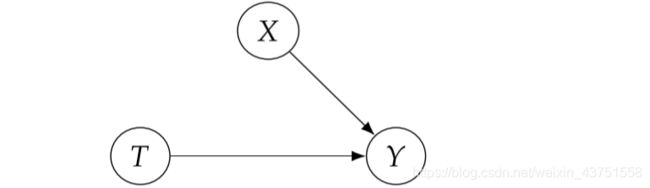
T : = t T:=t T:=t
Y : = f Y ( X , T , U Y ) Y:=f_{Y}\left(X, T, U_{Y}\right) Y:=fY(X,T,UY)
上述的例子中,控制T只改变了T的结构方程,其他变量的结构方程并没有发生改变,这也反映了模块化假设,即说明因果机制(结构方程)是模块化的。
对撞偏倚以及为什么条件集中不包含干预变量的后代节点
在为后门调整定义后门准则时,我们不仅指定调整集 W W W阻止所有后门路径,而且还指定 W W W不包含 T T T的任何后代。 为什么? 如果我们以 T T T的后代为条件,则可能会发生两类错误:
- 阻止因果关系从 T T T到 Y Y Y。
- 引起 T T T和 Y Y Y之间的非因果关联。
如果我们以从 T T T到 Y Y Y的有向路径上的节点为条件,那么我们将阻止因果关系沿该因果路径流动。 例如,在下面两个图中,控制 M M M分别阻塞了全部和部分因果路径。
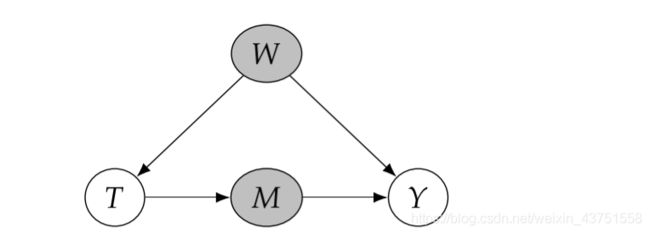
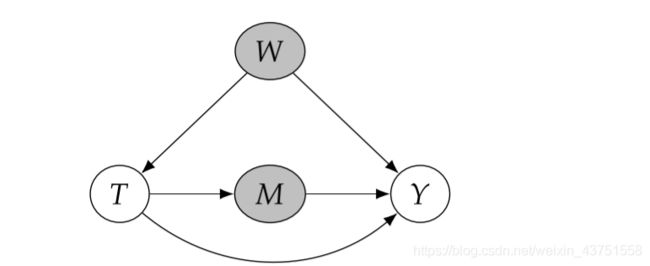
如果以不在从 T T T到 Y Y Y的有向路径上的 T T T的后代节点为条件,则它可能会打通被对撞节点阻塞的关联路径,如下图以Z为条件。
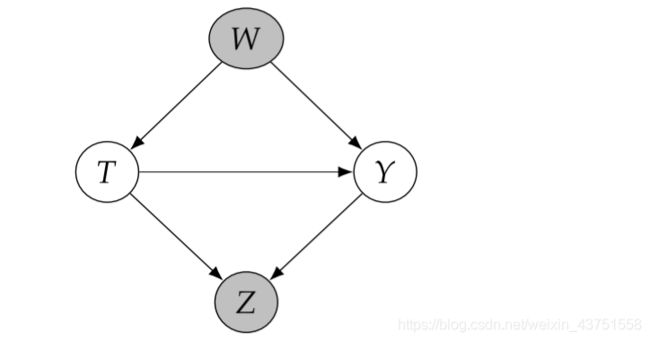
此外,对于下图,如果以Z为条件,会打通 T T T与 U M U_M UM之间的关联路径,从而对 T T T到 Y Y Y的因果路径产生影响。
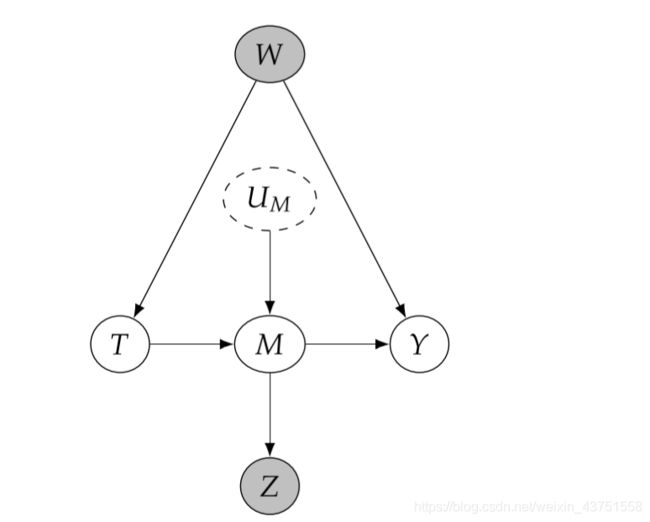
后门标准的这一准则通常被描述为:不以干预后变量为条件。
例子
问题:钠摄入量对血压的影响
数据:Luque-Fernandez et al. (2018)
干预T:钠摄入量(高于3.5mg值为1,否则为0)
结果Y:血压(连续)
协变量:W 年龄;Z 尿蛋白含量
首先画出因果图:
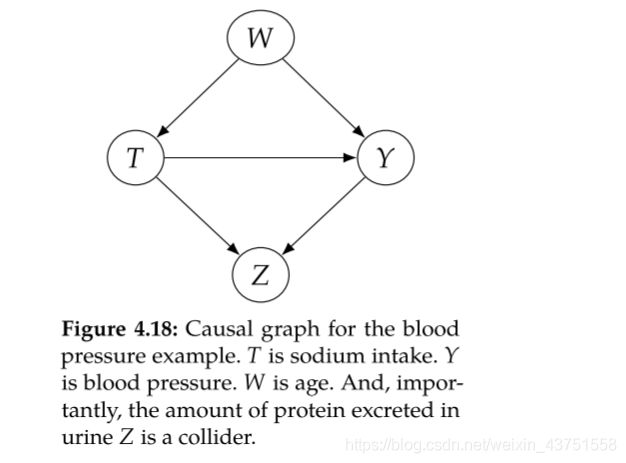
我们现在想要得到的是一个因果估计量: E ( Y ∣ d o ( t ) ) E(Y|do(t)) E(Y∣do(t))
分析因果图,要想得到因果估计量,需要进行后门调整,截断T←W→Y这条后门路径,因此需要控制W。注意,因果图中Z为对撞节点,不能对其进行控制。基于此,将因果估计量转为统计估计量: E W E [ Y ∣ t , W ] E_WE[Y|t,W] EWE[Y∣t,W]