Batch Normalization批量归一化

     深度学习捷报连连、声名鹊起，随机梯度下降成了训练深度网络的主流方法。尽管随机梯度下降法对于训练深度网络简单高效，但是它有个毛病，就是需要我们人为的去选择参数，比如学习率、参数初始化、权重衰减系数、Drop out比例等。这些参数的选择对训练结果至关重要，以至于我们很多时间都浪费在这些的调参上。那么学完这篇文献之后，你可以不需要那么刻意的慢慢调整参数。
      批量标准化一般用在非线性映射（激活函数）之前，对y=Wx+b进行规范化，使结果(输出信号的各个维度)的均值都为0,方差为1,让每一层的输入有一个稳定的分布会有利于网络的训练。

卷积层——BN层——激活层——池化层

BN层计算分为两步：

                                      

BN算法（Batch Normalization）其强大之处如下：

(1)你可以选择比较大的初始学习率，让你的训练速度飙涨。以前还需要慢慢调整学习率，甚至在网络训练到一半的时候，还需要想着学习率进一步调小的比例选择多少比较合适，现在我们可以采用初始很大的学习率，然后学习率的衰减速度也很大，因为这个算法收敛很快。当然这个算法即使你选择了较小的学习率，也比以前的收敛速度快，因为它具有快速训练收敛的特性；

(2)你再也不用去理会过拟合中drop out、L2正则项参数的选择问题，采用BN算法后，你可以移除这两项了参数，或者可以选择更小的L2正则约束参数了，因为BN具有提高网络泛化能力的特性；

(3)再也不需要使用使用局部响应归一化层了（局部响应归一化是Alexnet网络用到的方法，搞视觉的估计比较熟悉），因为BN本身就是一个归一化网络层；

(4)可以把训练数据彻底打乱（防止每批训练的时候，某一个样本都经常被挑选到，文献说这个可以提高1%的精度）。

总结一下：

1. 减少了参数的人为选择,可以取消dropout和L2正则项参数,或者采取更小的L2正则项约束参数
2. 减少了对学习率的要求
3. 可以不再使用局部响应归一化了,BN本身就是归一化网络(局部响应归一化-AlexNet)
4. 更破坏原来的数据分布,一定程度上缓解过拟合

        开始讲解算法前，先来思考一个问题：我们知道在神经网络训练开始前，都要对输入数据做一个归一化处理，那么具体为什么需要归一化呢？归一化后有什么好处呢？

1. 神经网络学习过程本质就是为了学习数据分布，一旦训练数据与测试数据的分布不同，那么网络的泛化能力也大大降低；
2. 另外一方面，一旦每批训练数据的分布各不相同(batch梯度下降)，那么网络就要在每次迭代都去学习适应不同的分布，这样将会大大降低网络的训练速度，这也正是为什么我们需要对数据都要做一个归一化预处理的原因。

       对于深度网络的训练是一个复杂的过程，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变，那么这一层网络就需要去适应学习这个新的数据分布，所以如果训练过程中，训练数据的分布一直在发生变化，那么将会影响网络的训练速度。

        我们知道网络一旦train起来，那么参数就要发生更新，除了输入层的数据外(因为输入层数据，我们已经人为的为每个样本归一化)，后面网络每一层的输入数据分布是一直在发生变化的，因为在训练的时候，前面层训练参数的更新将导致后面层输入数据分布的变化。以网络第二层为例：网络的第二层输入，是由第一层的参数和input计算得到的，而第一层的参数在整个训练过程中一直在变化，因此必然会引起后面每一层输入数据分布的改变。我们把网络中间层在训练过程中，数据分布的改变称之为：“Internal  Covariate Shift”。

     Internal Covariate Covariate：此术语是google小组在论文Batch BatchBatch Normalizatoin NormalizatoinNormalizatoin 中提出来的，其主要描述的是：训练深度网络的时候经常发生训练困难的问题，因为，每一次参数迭代更新后，上一层网络的输出数据经过这一层网络计算后，数据的分布会发生变化，为下一层网络的学习带来困难（神经网络本来就是要学习数据的分布，要是分布一直在变，学习就很难了）

一、Motivation

        作者认为：网络训练过程中参数不断改变导致后续每一层输入的分布也发生变化，而学习的过程又要使每一层适应输入的分布，因此我们不得不降低学习率、小心地初始化。作者将分布发生变化称之为 internal covariate shift。

       大家应该都知道，我们一般在训练网络的时会将输入减去均值，还有些人甚至会对输入做白化等操作，目的是为了加快训练。为什么减均值、白化可以加快训练呢？这里做一个简单地说明：

      首先，图像数据是高度相关的，假设其分布如下图a所示(简化为2维)。由于初始化的时候，我们的参数一般都是0均值的，因此开始的拟合y=Wx+b，基本过原点附近，如图b红色虚线。因此，网络需要经过多次学习才能逐步达到如紫色实线的拟合，即收敛的比较慢。如果我们对输入数据先作减均值操作，如图c，显然可以加快学习。更进一步的，我们对数据再进行去相关操作，使得数据更加容易区分，这样又会加快训练，如图d。   

二、初识BN(Batch  Normalization)

1、BN概述

       就像激活函数层、卷积层、全连接层、池化层一样，BN(Batch Normalization)也属于网络的一层。在前面我们提到网络除了输出层外，其它层因为低层网络在训练的时候更新了参数，而引起后面层输入数据分布的变化。这个时候我们可能就会想，如果在每一层输入的时候，再加个预处理操作那该有多好啊，比如网络第三层输入数据X3 (X3表示网络第三层的输入数据)把它归一化至：均值0、方差为1，然后再输入第三层计算，这样我们就可以解决前面所提到的“Internal Covariate Shift”的问题了。

      而事实上，paper的算法本质原理就是这样：在网络的每一层输入的时候，又插入了一个归一化层，也就是先做一个归一化处理，然后再进入网络的下一层。不过文献归一化层，可不像我们想象的那么简单，它是一个可学习、有参数的网络层。既然说到数据预处理，下面就先来复习一下最强的预处理方法：白化。

2、预处理操作选择

      说到神经网络输入数据预处理，最好的算法莫过于白化预处理。白化的方式有好几种，常用的有PCA白化（由于原始数据存在冗余，通过PCA降维，使用最低维度来表达数据，消除冗余，减速训练）：即对数据进行PCA操作之后，在进行方差归一化。这样数据基本满足0均值、单位方差、弱相关性。作者首先考虑，对每一层数据都使用白化操作，但分析认为这是不可取的。因为白化需要计算协方差矩阵、求逆等操作，计算量很大，此外，反向传播时，白化操作不一定可导。所以在深度学习中，其实很少用到白化。经过白化预处理后，数据满足条件：a、特征之间的相关性降低，这个就相当于pca；b、数据均值、标准差归一化，也就是使得每一维特征均值为0，标准差为1。如果数据特征维数比较大，要进行PCA，也就是实现白化的第1个要求，是需要计算特征向量，计算量非常大，于是为了简化计算，作者忽略了第1个要求，采用Normalization方法。仅仅使用了下面的公式进行预处理。归一化公式(公式中k为通道channel数)：

                                                     
       后面我们也将用这个公式，对某一个层网络的输入数据做一个归一化处理。需要注意的是，我们训练过程中采用batch随机梯度下降，上面的指的是每一批训练数据神经元的平均值；然后分母就是每一批数据神经元激活度的一个标准差了。 

三、BN算法实现

1、BN算法概述

       经过前面简单介绍，这个时候可能我们会想当然的以为：好像很简单的样子，不就是在网络中间层数据做一个归一化处理嘛,然而其实实现起来并不是那么简单的。其实如果是仅仅使用上面的归一化公式，对网络某一层A的输出数据做归一化，然后送入网络下一层B，这样是会影响到本层网络A所学习到的特征的。打个比方，比如我网络中间某一层学习到特征数据本身就分布在S型激活函数的两侧，你强制把它给我归一化处理、标准差也限制在了1，把数据变换成分布于s函数的中间部分，这样就相当于我这一层网络所学习到的特征分布被你搞坏了，如果简单的这么干，会降低层的表达能力。比如下图，在使用sigmoid激活函数的时候，如果把数据限制到0均值单位方差，那么相当于只使用了激活函数中近似线性的部分，这显然会降低模型表达能力。 

减均值除方差：远离饱和区

                     

              

     a中左图是没有经过任何处理的输入数据，曲线是sigmoid函数，如果数据在梯度很小的区域，那么学习率就会很慢甚至陷入长时间的停滞。减均值除方差后，数据就被移到中心区域如右图所示，对于大多数激活函数而言，这个区域的梯度都是最大的或者是有梯度的（比如ReLU），这可以看做是一种对抗梯度消失的有效手段。对于一层如此，如果对于每一层数据都那么做的话，数据的分布总是在随着变化敏感的区域，相当于不用考虑数据分布变化了，这样训练起来更有效率。这有两个好处：1、避免分布数据偏移；2、远离导数饱和区。

      那么为什么要有第4步，不是仅使用减均值除方差操作就能获得目的效果吗？我们思考一个问题，减均值除方差得到的分布是正态分布，我们能否认为正态分布就是最好或最能体现我们训练样本的特征分布呢？不能，比如数据本身就很不对称（不符合正态分布），或者激活函数未必是对方差为1的数据最好的效果，比如Sigmoid激活函数，在-1~1之间的梯度变化不大，那么非线性变换的作用就不能很好的体现，BN变换后就没有达到非线性变换的目的。而对于relu，效果会更差，因为会有一半的置零。总之换言之，减均值除方差操作后可能会削弱网络的性能。针对该情况，在前面三步之后加入第4步完成真正的batch normalization。

      BN的本质就是利用优化变一下方差大小和均值位置，使得新的分布更切合数据的真实分布，保证模型的非线性表达能力。BN的极端的情况就是这两个参数等于mini-batch的均值和方差，那么经过batch normalization之后的数据和输入完全一样，当然一般的情况是不同。

缩放加移位：避免线性区

    因此，必须进行一些转换变换重构，才能将分布从0移开。为BN增加了2个可学习参数γ、β，用来保持模型的表达能力。使用缩放因子γ和移位因子β来执行此操作。这就是算法关键之处：

                                                                    
    尺度变换和偏移：将xi乘以γ调整数值大小，再加上β增加偏移后得到yi，这一步是BN的精髓，由于归一化后的xi基本会被限制在正态分布下，使得网络的表达能力下降。为解决该问题，我们引入两个新的参数：γ,β。
from：https://blog.csdn.net/vict_wang/article/details/88075861

式中m表示该批次的样本个数。

     如果直接做归一化不做其他处理，神经网络是学不到任何东西的，但是加入这两个参数后，事情就不一样了，每一个神经元都会有一对这样的参数γ、β，先考虑特殊情况下，如果γ 和β分别等于此batch的标准差和均值

                                 、，

     那么xi不就还原到归一化前的x了，也即是缩放平移到了归一化前的分布，相当于batchnorm没有起作用，β 和γ分别称之为平移参数和缩放参数 。这样就保证了每一次数据经过归一化后还保留的有学习来的特征，同时又能完成归一化这个操作，加速训练。

     因此我们引入了这个可学习重构参数γ、β，让我们的网络可以学习恢复出原始网络所要学习的特征分布。

                                    

（我的理解：由于x归一化成,传入下一层，继续进行神经网络计算，这种方法会丢失一些特征，而引入γ、β参数，来保存由该层所学到特征（这些特征没有带入到下一网络层进行计算））这种理解应该是错的。引入γ、β是为了将样本从线性区平移缩放到非线性区（不会到饱和区）

最后Batch Normalization网络层的前向传导过程公式就是：

                                                              

上面的公式中m指的是mini-batch的size。

反向传播过程

                   

注意公式4和公式3的关系

def batchnorm_backward(dout, cache):
  """ Backward pass for batch normalization.
  - dout: Upstream derivatives, of shape (N, D)
  - cache: Variable of intermediates from batchnorm_forward.  
  - dx: Gradient with respect to inputs x, of shape (N, D)
  - dgamma: Gradient with respect to scale parameter gamma, of shape (D,)
  - dbeta: Gradient with respect to shift parameter beta, of shape (D,)
  """ 
 mode = cache[0]
  if mode == 'train':
    mode, x, gamma, xc, std, xn, out = cache
    N = x.shape[0]
    dbeta = dout.sum(axis=0)#公式6
    dgamma = np.sum(xn * dout, axis=0)#xn是标准化后的样本值,公式5
    dxn = gamma * dout  #公式1
    dxc = dxn / std
    dstd = -np.sum((dxn * xc) / (std * std), axis=0)  #xc = x - mean，公式2
    dvar = 0.5 * dstd / std                                       #公式2
    dxc += (2.0 / N) * xc * dvar                         #公式3右半部分
    dmu = np.sum(dxc, axis=0)
    dx = dxc - dmu / N  #公式4
  elif mode == 'test':
    mode, x, xn, gamma, beta, std = cache
    dbeta = dout.sum(axis=0)
    dgamma = np.sum(xn * dout, axis=0)
    dxn = gamma * dout
    dx = dxn / std
  else:
    raise ValueError(mode)
return dx, dgamma, dbeta

from： https://www.jianshu.com/p/434020d4bd2f

def Batchnorm_simple_for_train(x, gamma, beta, bn_param):
"""
param:x    : 输入数据，设shape(B,L)
param:gama : 缩放因子  γ
param:beta : 平移因子  β
param:bn_param   : batchnorm所需要的一些参数
eps      : 接近0的数，防止分母出现0
momentum : 动量参数，一般为0.9， 0.99， 0.999
running_mean ：滑动平均的方式计算新的均值，训练时计算，为测试数据做准备
running_var  : 滑动平均的方式计算新的方差，训练时计算，为测试数据做准备
"""
running_mean = bn_param['running_mean']  #shape = [B]
running_var = bn_param['running_var']    #shape = [B]
results = 0. # 建立一个新的变量    
x_mean=x.mean(axis=0)  # 计算x的均值
x_var=x.var(axis=0)    # 计算方差
x_normalized=(x-x_mean)/np.sqrt(x_var+eps)       # 归一化
results = gamma * x_normalized + beta            # 缩放平移

running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var
    
    #记录新的值
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var 
    
return results , bn_param

     测试：测试的时候每次只输入一张图片，这怎么计算批量的均值和方差，在训练的时候实现计算好mean var，测试的时候直接拿来用就可以了，不用计算均值和方差。

def Batchnorm_simple_for_test(x, gamma, beta, bn_param):
"""
param:x    : 输入数据，设shape(B,L)
param:gama : 缩放因子  γ
param:beta : 平移因子  β
param:bn_param   : batchnorm所需要的一些参数
eps      : 接近0的数，防止分母出现0
momentum : 动量参数，一般为0.9， 0.99， 0.999
running_mean ：滑动平均的方式计算新的均值，训练时计算，为测试数据做准备
running_var  : 滑动平均的方式计算新的方差，训练时计算，为测试数据做准备
"""
	running_mean = bn_param['running_mean']  #shape = [B]
     running_var = bn_param['running_var']    #shape = [B]
	results = 0. # 建立一个新的变量
   
    x_normalized=(x-running_mean )/np.sqrt(running_var +eps)       # 归一化
    results = gamma * x_normalized + beta            # 缩放平移
    
return results , bn_param

2、源码实现

def batch_norm_layer(x, train_phase, scope_bn):
    with tf.variable_scope(scope_bn):
		# 新建两个变量，平移、缩放因子
        beta = tf.Variable(tf.constant(0.0, shape=[x.shape[-1]]), name='beta', trainable=True)
        gamma = tf.Variable(tf.constant(1.0, shape=[x.shape[-1]]), name='gamma', trainable=True)
        
        # 计算此次批量的均值和方差
        axises = np.arange(len(x.shape) - 1)
        batch_mean, batch_var = tf.nn.moments(x, axises, name='moments')

		# 滑动平均做衰减
        ema = tf.train.ExponentialMovingAverage(decay=0.5)

        def mean_var_with_update():
            ema_apply_op = ema.apply([batch_mean, batch_var])
            with tf.control_dependencies([ema_apply_op]):
                return tf.identity(batch_mean), tf.identity(batch_var)
        # train_phase 训练还是测试的flag
		# 训练阶段计算runing_mean和runing_var，使用mean_var_with_update（）函数
		# 测试的时候直接把之前计算的拿去用 ema.average(batch_mean)
        mean, var = tf.cond(train_phase, mean_var_with_update,
                            lambda: (ema.average(batch_mean), ema.average(batch_var)))
        normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)
    return normed

   （求一个batch的均值，对batch的所有的样本采用滑动平均，先求出一个样本，再接着求下一个样本。。。）滑动平均的好处：占内存少，不需要保存过去10个或者100个历史θθ值，就能够估计其均值。（当然，滑动平均不如将历史值全保存下来计算均值准确，但后者占用更多内存和计算成本更高）https://www.cnblogs.com/wuliytTaotao/p/9479958.html

3、实战使用

(1)需要注意的一点是Batch Normalization在training和testing时行为有所差别。Training时均值u和σ由当前batch计算得出；在Testing时μ和σ应使用Training时保存的均值或类似的经过处理的值，而不是由当前batch计算。网络一旦训练完毕，参数都是固定的。

      实际测试网络的时候，我们依然会应用下面的式子： 
                                                                  
特别注意： 这里的均值和方差已经不是针对某一个Batch了，而是针对整个数据集而言。因此，在训练过程中除了正常的前向传播和反向求导之外，我们还要记录每一个Batch的均值和方差，以便训练完成之后按照下式计算整体的均值和方差： 

                                                                      

    上面简单理解就是：对于均值来说直接计算所有batch的均值u值的平均值；然后对于标准偏差采用每个batch的的无偏估计。最后测试阶段，BN的使用公式就是：

                                                                     

(2)根据文献说，BN可以应用于一个神经网络的任何神经元上。文献主要是把BN变换，置于网络激活函数层的前面。在没有采用BN的时候，激活函数层是这样的：

                                                                               

也就是我们希望一个激活函数，比如s型函数s(x)的自变量x是经过BN处理后的结果。因此前向传导的计算公式就应该是：

                                                                            

    其实因为偏置参数b经过BN层后其实是没有用的，最后也会被均值归一化，当然BN层后面还有个β参数作为偏置项，所以b这个参数就可以不用了。因此最后把BN层+激活函数层就变成了：

                                                                              

四、Batch Normalization在CNN中的使用

       通过上面的学习，我们知道BN层是对于每个神经元做归一化处理，甚至只需要对某一个神经元进行归一化，而不是对一整层网络的神经元进行归一化。既然BN是对单个神经元的运算，那么在CNN中卷积层上要怎么搞？假如某一层卷积层有6个特征图，每个特征图的大小是100*100，这样就相当于这一层网络有6*100*100个神经元，如果采用BN，就会有6*100*100个参数γ、β，这样岂不是太恐怖了。因此卷积层上的BN使用，其实也是使用了类似权值共享的策略，把一整张特征图当做一个神经元进行处理。

       卷积神经网络经过卷积后得到的是一系列的特征图，如果min-batch sizes为m，那么网络某一层输入数据可以表示为四维矩阵(m,c,p,q)，m为min-batch sizes，c为特征图个数，p、q分别为特征图的宽高。在cnn中我们可以把每个特征图看成是一个特征处理（一个神经元），因此在使用Batch Normalization，mini-batch size的大小就是：m*p*q，于是对于每个特征图都只有一对可学习参数：γ、β。（就是说批量归一化层的参数个数为特征图通道数的2倍，即：c*2）

     这就是相当于求：所有样本所对应的一个特征图的所有神经元的平均值、方差，然后对这个特征图神经元做归一化。下面是来自于keras卷积层的BN实现一小段主要源码：

           input_shape = self.input_shape
            reduction_axes = list(range(len(input_shape)))
            del reduction_axes[self.axis]
            broadcast_shape = [1] * len(input_shape)
            broadcast_shape[self.axis] = input_shape[self.axis]
            if train:
                m = K.mean(X, axis=reduction_axes)
                brodcast_m = K.reshape(m, broadcast_shape)
                std = K.mean(K.square(X - brodcast_m) + self.epsilon, axis=reduction_axes)
                std = K.sqrt(std)
                brodcast_std = K.reshape(std, broadcast_shape)
                mean_update = self.momentum * self.running_mean + (1-self.momentum) * m
                std_update = self.momentum * self.running_std + (1-self.momentum) * std
                self.updates = [(self.running_mean, mean_update),
                                (self.running_std, std_update)]
                X_normed = (X - brodcast_m) / (brodcast_std + self.epsilon)
            else:
                brodcast_m = K.reshape(self.running_mean, broadcast_shape)
                brodcast_std = K.reshape(self.running_std, broadcast_shape)
                X_normed = ((X - brodcast_m) /
                            (brodcast_std + self.epsilon))
            out = K.reshape(self.gamma, broadcast_shape) * X_normed + K.reshape(self.beta, broadcast_shape)

采用这个方法网络的训练速度快到惊人啊，感觉训练速度是以前的十倍以上，再也不用担心自己这破电脑每次运行一下，训练一下都要跑个两三天的时间。

五、BN with TF

      BN在TensorFlow中主要有两个函数:tf.nn.moments以及tf.nn.batch_normalization,两者需要配合使用,前者用来返回均值和方差,后者用来进行批处理(BN)

1、tf.nn.moments：

该函数返回两个张量，均值mean和方差variance。

moments(
    x,
    axes,
    shift=None,
    name=None,
    keep_dims=False
)

    其中参数 x 为要传递的tensor,axes传递要进行计算的维度， 即想要 normalize的维度, [0] 代表 batch 维度，如果是图像数据，可以传入 [0, 1, 2]，相当于求[batch, height, width] 的均值/方差，注意不要加入channel 维度。

我们需要利用这个函数计算出BN算法需要的前两项：

# 计算Wx_plus_b 的均值与方差,其中axis = [0] 表示想要标准化的维度
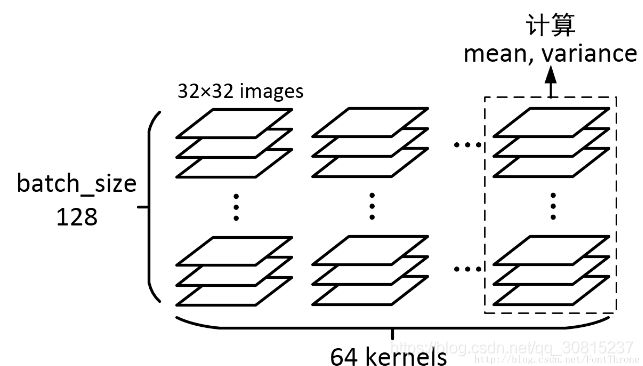
img_shape= [128, 32, 32, 64]
Wx_plus_b = tf.Variable(tf.random_normal(img_shape))
axis = list(range(len(img_shape)-1))               # [0,1,2] 
wb_mean, wb_var = tf.nn.moments(Wx_plus_b, axis)

函数说明：tf.random_normal用于从正态分布中输出随机值。

random_normal(shape,mean=0.0,stddev=1.0,dtype=tf.float32,seed=None,name=None)

• shape：一个一维整数张量或Python数组。代表张量的形状。
• mean：数据类型为dtype的张量值或Python值。是正态分布的均值。
• stddev：数据类型为dtype的张量值或Python值。是正态分布的标准差。
• dtype： 输出的数据类型。
• seed：一个Python整数。是随机种子。
• name： 操作的名称(可选)

运行结果：均值为0，方差为1

*** wb_mean ***
[  1.05310767e-03   1.16801530e-03   4.95071337e-03  -1.50891789e-03
  -2.95298663e-03  -2.07848335e-03  -3.81800164e-05  -3.11688287e-03
   3.26496479e-03  -2.68524280e-04  -2.08893605e-03  -3.05374013e-03
   1.43721583e-03  -3.61034041e-03  -3.03616724e-03  -1.10225368e-03
   6.14093244e-03  -1.37914100e-03  -1.13333750e-03   3.53972078e-03
  -1.48577197e-03   1.04353309e-03   3.27868876e-03  -1.40919012e-03
   3.09609319e-03   1.98166977e-04  -5.25404140e-03  -6.03850756e-04
  -1.04614964e-03   2.90997117e-03   5.78491192e-04  -4.97420435e-04
   3.03052540e-04   2.46527663e-04  -4.70882794e-03   2.79057049e-03
  -1.98713480e-03   4.13944060e-03  -4.80978837e-04  -3.90357309e-04
   9.11145413e-04  -4.80215019e-03   6.26503082e-04  -2.76877987e-03
   3.79961479e-04   5.36157866e-04  -2.12549698e-03  -5.41620655e-03
  -1.93006988e-03  -8.54363534e-05   4.97094262e-03  -2.45843385e-03
   4.16610064e-03   2.44746287e-03  -4.15429426e-03  -6.64028199e-03
   2.56747357e-03  -1.63110415e-03  -1.53350492e-03  -7.66420271e-04
  -1.81624549e-03   2.16634944e-03   1.74984348e-03  -4.17272677e-04]
*** wb_var ***
[ 0.99813616  0.9983741   1.00014114  1.0012747   0.99496585  1.00168002
  1.00439012  0.99607879  1.00104094  0.99969071  1.01024568  0.99614906
  1.00092578  0.99977148  1.00447345  0.99580348  0.99797201  0.99119431
  1.00352168  0.9958936   0.99980813  1.00598109  1.00050855  0.99667317
  0.99352562  1.0036608   0.99794698  0.99324805  0.99862647  0.99930048
  0.99658304  1.00278556  0.99731135  1.00254881  0.99352133  1.00371397
  1.00258803  1.00388253  1.00404358  0.99454063  0.99434716  1.00087452
  1.00818515  1.00019705  0.99542576  1.00410056  0.99707311  1.00215423
  1.00199771  0.99394888  0.9973973   1.00197709  0.99835181  0.99944276
  0.99977624  0.99892712  0.99871159  0.99913275  1.00471914  1.00210452
  0.99568754  0.99547535  0.99983472  1.00523198]**重点内容**

我们假设图片的shape[128, 32, 32, 64],64表示通道数，它的运算方式如图:

                   

详细过程： 

   

      从上图卷积过程可以得出一张5*5的图片经过卷积核3*3的卷积之后得到一张3*3的特征图。特征图就会包含了9个特征值，这9个特征值就是我们上面所提到的样本。假设我们的batch-size设为m，那么就会有m*9个特征值传到BN层里面作为样本来训练参数γ和β。在网络训练中以batch-size作为最小单位来不断迭代。每当有新的batch-size进入到网络里面就会产生新的γ和β。也就是说我们训练过程中要生成图片总量/batch-size 组参数。图像卷积的过程中，通常是使用多个卷积核，得到多张特征图，对于多个的卷积核需要保存多个的γ与β。

输入：待进入激活函数的变量 
输出： 
1.这里的K，在卷积网络中可以看作是卷积核个数，如网络中第n层有64个卷积核，就需要计算64次。 
   需要注意，在正向传播时，会使用γ与β使得BN层输出与输入一样。 
2.在反向传播时利用γ与β求得梯度从而改变训练权值（变量）。 
3.通过不断迭代直到训练结束，求得关于不同层的γ与β。
4.不断遍历训练集中的图片，取出每个batch_size中的γ与β，最后统计每层BN的γ与β各自的和除以图片数量得到平均直，并对其    做无偏估计直作为每一层的E[x]与Var[x]。 
5.在预测的正向传播时，对测试数据求取γ与β，并使用该层训练时的E[x]与Var[x]，通过图中公式11计算BN层输出。 
注意，在预测时，BN层的输出已经被改变，所以BN层在预测的作用体现在此处。
from：https://blog.csdn.net/donkey_1993/article/details/81871132

2、tf.nn.batch_normalization

batch_normalization(
    x,
    mean,
    variance,
    offset,
    scale,
    variance_epsilon,
    name=None
)

• x：代表任意维度的输入张量。
• mean:代表样本的均值。
• variance：代表样本的方差。
• offset：代表偏移，即相加一个转化值，也是公式中的beta。
• scale：代表缩放，即乘以一个转化值，也是公式中的gamma。
• variance_epsilon：是为了避免分母为0的情况下，给分母加上的一个极小值，默认即可。
• name：名称。

scale = tf.Variable(tf.ones([64]))
offset = tf.Variable(tf.zeros([64]))
variance_epsilon = 0.001
Wx_plus_b = tf.nn.batch_normalization(Wx_plus_b, wb_mean, wb_var, offset, scale, variance_epsilon)

# 根据公式我们也可以自己写一个
Wx_plus_b1 = (Wx_plus_b - wb_mean) / tf.sqrt(wb_var + variance_epsilon)
Wx_plus_b1 = Wx_plus_b1 * scale + offset
# 因为底层运算方式不同,实际上自己写的最后的结果与直接调用tf.nn.batch_normalization获取的结果并不一致。

#Wx_plus_b
[[[[  3.32006335e-01  -1.00865233e+00   4.68401730e-01 ...,
     -1.31523395e+00  -1.13771069e+00  -2.06656289e+00]
   [  1.92613199e-01  -1.41019285e-01   1.03402412e+00 ...,
      1.66336447e-01   2.34183773e-01   1.18540943e+00]
   [ -7.14844346e-01  -1.56187916e+00  -8.09686005e-01 ...,
     -4.23679769e-01  -4.32125211e-01  -3.35091174e-01]
   ...,

from：https://blog.csdn.net/hjimce/article/details/50866313

from：https://blog.csdn.net/fontthrone/article/details/76652772

from：https://blog.csdn.net/shuzfan/article/details/50723877

form :https://www.cnblogs.com/king-lps/p/8378561.html