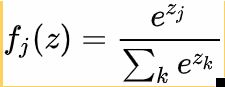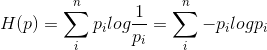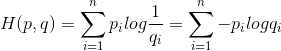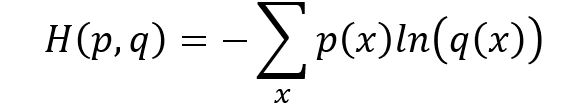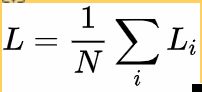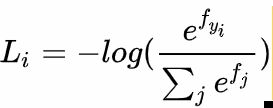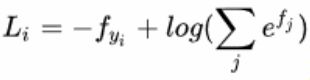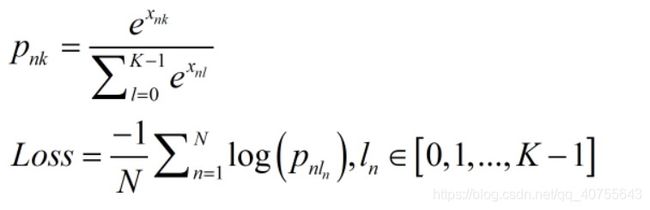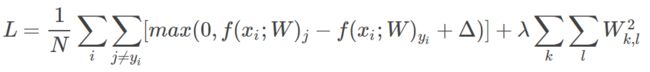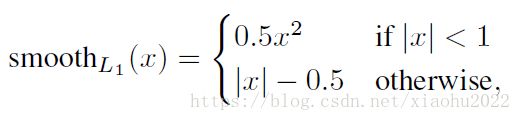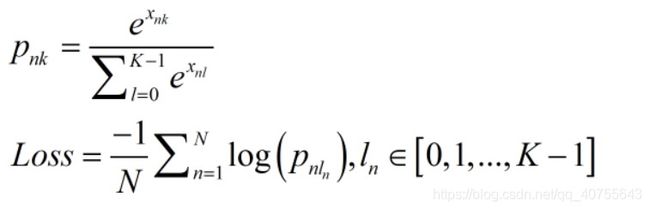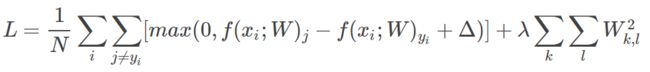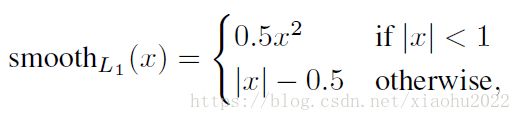神经网络损失函数
sotfmax损失
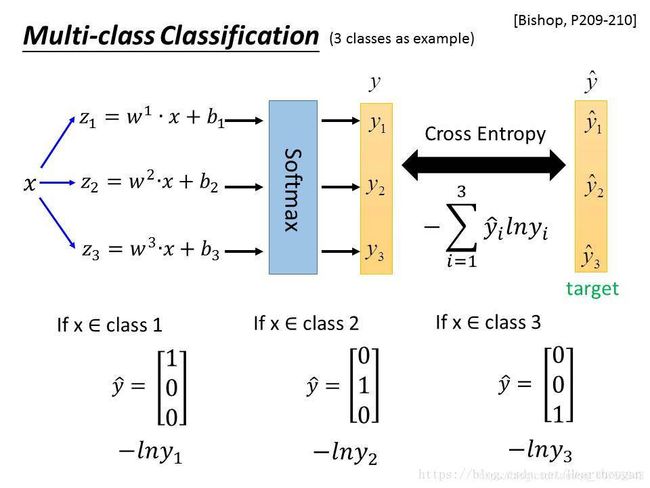
1.softmax分类器:
softmax函数:其输入值是一个向量(图像),向量中元素为任意实数的评分值(中的),函数对其进行压缩,输出一个向量,其中每个元素值在0到1之间,且所有元素之和为1。softmax相当于是对输入做了一个归一化处理,其结果相当于输入图像被分到每个标签的概率分布。该函数是单调增函数,即输入值越大,输出也就越大,输入图像属于该标签的概率就越大。
假设有K个类别,Softmax计算过程为:其中,j=0,1,2,3,4,5,...,K-1
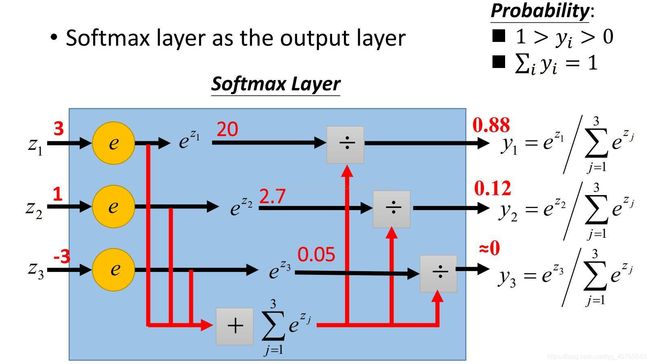
计算过程如下图:
2.cross-entropy loss:
假设和是关于样本集的两个分布,其中是样本集的真实分布,是样本集的估计分布,那么按照真是分布来衡量识别一个样本所需要编码长度的期望(即,平均编码长度):
如果用估计分布来表示真实分布的平均编码长度,应为:
这是因为用来编码的样本来自于真是分布,所以期望值中的概率是。而就是交叉熵。
所以原始交叉熵函数公式:
首先,熵是信息论里面一个概念,用来衡量信息的不确定性,信息的不确定性越大,熵就越大。那么信息的不确定性跟什么有关系呢?答案就是概率。那么交叉的意思就是需要两样东西,所以在这里两样东西就是两个不同的概率分布p和q,交叉熵就是来衡量这两个概率分布的相似情况。我们的目标是让值两个概率分布越接近越好(一个是标签label,另一个则是网络的输出)。假设q是真实的标签,p是网络的输出,我们通过cross entropy loss 和BP算法(误差反向传播)来让p越来越接近q,即在完全知道q的信息量的情况下去不断的窥探q分布的信息量,慢慢的,我们也知道了q分布到底是什么,这个时候两者的交叉熵就很小了,q的不确定性没剩下多少了。
3.softmax交叉熵损失函数:
sottmax对数释然:
其中表示分类评分向量中的第j个元素。
或:
因为softmax计算的值是图像分到每个类别标签的相对概率,所以对该相对概率取-log值就是这组数据正确分类的Softmax值,它占的比重越大,这个样本的Loss也就越小。也就是分类得越准确即对某类的相对概率就越大,则样本得loss就会越小。
举个栗子:
mnist的label是什么呢?答:是用one-hot编码的一组向量,0-9的编码(label)如下:
损失函数公式:
第一个公式就是softmax,其中x是样本,k表示类别,softmax是用于多分类,每次扔进去的是一个向量。在mnist的例子中每一个样本都是用10维向量来表示的,10维向量的每一维都不独立,并且是one-hot编码,只有一维是1,其他维度都是0,完美的匹配了sotfmax输入的要求。所以每次扔进sotfmax的是表示某一个数字的向量。
再看第二个公式,把第一个公式带入交叉熵的原始形式就可以得到这个公式,N表示mini-batch的样本数,p就是第一个公式的那个p,one-hot 编码的label只有一个1,所以10个维度的p(x)和q(x)计算交叉熵就只剩下一个维度了。公式很好推就不推了。
当某一次输入到网络中的是x,x表示某个数字,如果x与它对应的label y差的很远,那么loss很大,梯度回传进行参数更新。直到loss变的很小。
SVM损失
也称为折页损失(hinge loss)。
SVM的损失函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值,也就是间隔,一般取1。
eg:第i个数据中包含图像的像素和代表正确类别的标签。
则第i个数据针对第j个类别的得分:![]()
用例子演示公式是如何计算的。假设有3个分类,并且得到了分值。其中第一个类别是正确类别,即。同时假设是10(后面会详细介绍该超参数)。上面的公式是将所有不正确分类()加起来,所以我们得到两个部分:
将损失函数改写下:
其中是权重的第j行,被变形为列向量。
整个训练集合上的平均损失,包括正则项,则公式如下:
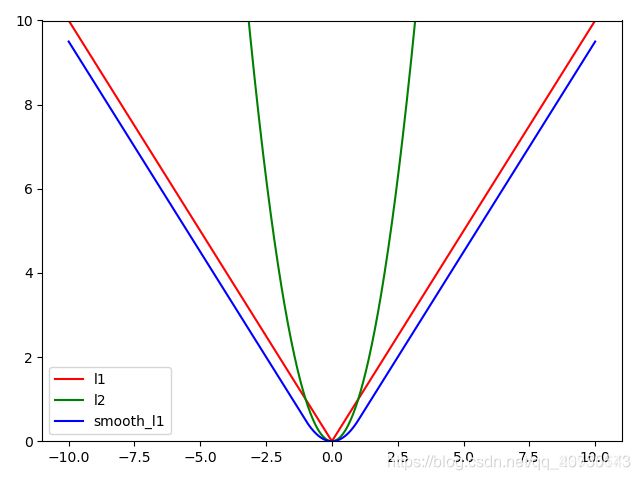
SmoothL1损失
一般用于边框回归,由L1损失和L2损失组成。
为什么选择这样的组合?
因为避免梯度爆炸,且对噪声点更加鲁棒。
当loss处于[-1,1]之间时,使用L2损失,梯度下降同 L2,比较缓慢,不至于在最优值左右来回震荡;
当loss处于[−∞,-1],[1,+∞],使用L1损失,梯度下降同 L1,避免了 l2的梯度爆炸情况;同时,对于噪声也没有L2敏感,增强了抗噪性。
举个栗子:
当有个离群点与目标的距离x=100,若使用L2损失则loss=5000,而使用L1损失,loss=99.5。
总结
1.softmax损失:
2.svm损失:
3.smoothL1损失: