采用POD以及DMD方法实现圆柱绕流流动分解(POD篇)
背景
笔者通过对POD及DMD两种模型降阶方法进行学习后,尝试对Brunton大佬书中Re=100圆柱绕流case进行复现,现将学习及复现过程的代码及结果进行分享,希望多提宝贵建议。
本文圆柱绕流案例采用的Data文件以及原代码可以在这里下载到,书1中的原有代码写的也很好,但无法复现书中精美的结果,本文在书中原有代码的基础上,结合对文献2以及博客文章3和4的学习,重新整理了相关代码并对结果进行复现。写下这篇博文是对学习过程的梳理及总结,同时供大家交流参考。
关于POD以及DMD的相关背景知识,所列参考文献中讲解的非常清楚,有这方面需求的小伙伴请移步参考文献,建议零基础的同学先看文献3和4然后再开始本文的学习。
POD(本征正交分解)是一种处理大量数据的方法, 在流场模态分解、 模型降阶方面有很好的应用。此法按照能量等级的差异将流场分解为不同的模态,各个模态为正交基函数与时间函数的乘积,可以看做一个具有特定能量幅值的时变的流动结构,其本质是将随时间变化的原始信号(流场)投影到一组随时间变化的,相互正交的空间信号(流场)的叠加。
Re=100圆柱绕流算例
CFD计算的具体参数以及网格时间尺度参数详见下表
| 项目 | Value |
|---|---|
| R e Re Re | 100 |
| Δ t \Delta t Δt | 0.02 |
| S n a p s h o t s Snapshots Snapshots | 150 |
| S t St St | 0.16 |
| n x nx nx | 199 |
| n y ny ny | 449 |
CFD计算的瞬态流场(IBM方法)
%% POD_Cylinder Wake
clc
clear
close all
load CYLINDER_ALL.mat;
X=VORTALL';
Y=[X;X];
[U0x,An,phiU,Ds]=POD_SVD_M(Y);
%% 简单看一下瞬态计算结果,顺便保存个gif图片
pic_num = 1;
for i=1:100
clf
plotCylinder_m(reshape(VORTALL(:,i),nx,ny),nx,ny);
%hold on
pause(0.05)
F=getframe(gcf);
I=frame2im(F);
[I,map]=rgb2ind(I,256);
if pic_num == 1
imwrite(I,map,'test4.gif','gif','Loopcount',inf,'DelayTime',0.2);
else
imwrite(I,map,'test4.gif','gif','WriteMode','append','DelayTime',0.2);
end
pic_num = pic_num + 1;
end
%% 查看一下平均流场的信息,并保存图片
plotCylinder_m(reshape(U0x,nx,ny),nx,ny);
print(gcf, '-dpng', '-r600', './U0x.png');
%% 动态展示前十阶POD分解模态结果
for k=1:10
clf
plotCylinder_m(reshape(An(1,k).*phiU(:,k),nx,ny),nx,ny);
drawnow
pause(0.1)
end
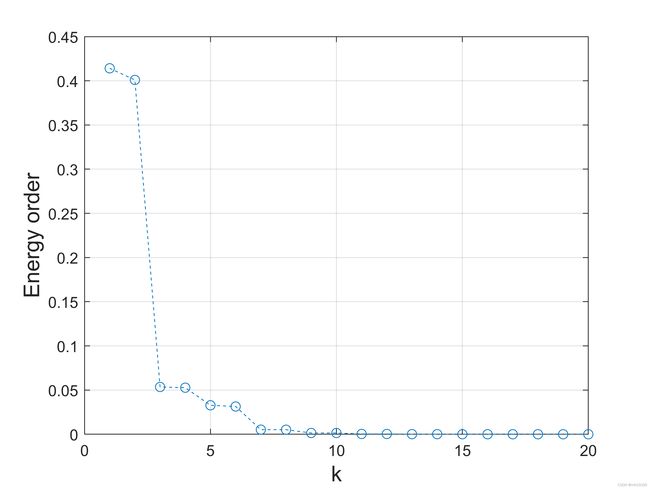
%% 前二十模态能量大小(SVD具有自动排序功能,不需要再对特征值大小进行排序)
figure(1)
plot(1:20,Ds(1:20)/sum(Ds),'o--');
ylabel('Energy order','FontName','Arial', 'FontSize',14);
xlabel('k','FontName','Arial', 'FontSize',14);
grid on
name1=['Energy order.png'];
print(gcf, '-dpng', '-r600',name1);
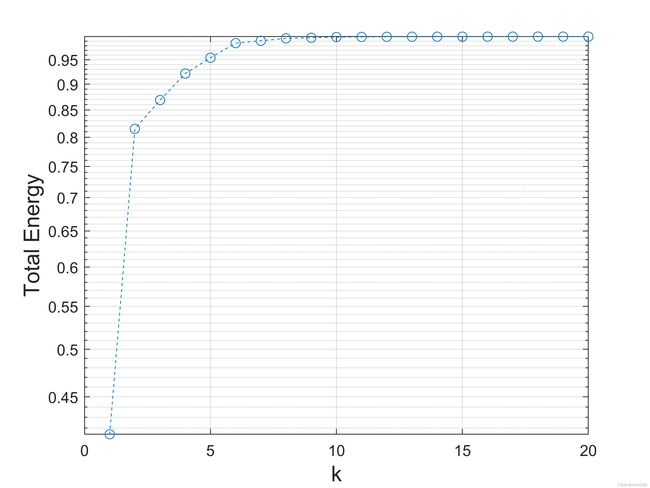
figure(2)
semilogy(1:20,cumsum(Ds(1:20))/sum(Ds),'o--');
ylabel('Total Energy','FontName','Arial', 'FontSize',14);
xlabel('k','FontName','Arial', 'FontSize',14);
grid on
name2=['Energy cum.png'];
print(gcf, '-dpng', '-r600',name2);
%% 前6阶模态叠加还原流场
Sigma=zeros(size(phiU));
for i=1:6
V{i}=An(:,i).*phiU(:,i)';
Sigma=Sigma+V{i}';
end
for j=1:100
clf
plotCylinder_m(reshape(Sigma(:,j)'+U0x,nx,ny),nx,ny);
pause(0.05)
end
上述代码每一个模块可以单独运行,可以看出前六阶模态的叠加已经可以很好的还原流动细节。POD算法的代码以及后处理图片的代码如下所示:
function [U0x,An,phiU,Ds]=POD_SVD_M(Utx)
%2022.2.18
%SVD-POD算法
%输入Utx,其中时间离散长度N=size(Utx,1),空间离散长度m=size(Utx,2)
%输出U0x,0阶模态,可以看做定常平均值
%输出An:时间变量,对应模态的幅值随时间的变化,可以用来做时间序列分析
%输出phiU:POD的模态
%输出Ds:特征值Ds反映了每一个模态对应的能量,可以用来排序
m=size(Utx,2);%空间长度
N=size(Utx,1);%时间长度
%除去稳态值
U0x=mean(Utx,1);
Utx=Utx-U0x.*ones(N,m);
[U,S,phiU]=svd(Utx,'econ');
An=U*S;
Ds=diag(S).^2/N;
end
function f1=plotCylinder_m(VORT,ny,nx)
%2022.2.19
%流场后处理
%输入变量VORT,为空间变量转化为列向量的流场快照矩阵
%输入变量ny,nx,为空间尺度大小
pcolor(VORT);
shading interp;
load CCcool.mat
colormap(CC);
caxis([-min(abs(min(min(VORT))),max(max(VORT))),min(abs(min(min(VORT))),max(max(VORT)))]);
%重置坐标轴
set(gca,'XTick',[1 50 100 150 200 250 300 350 400 449],'XTickLabel',{'-1','0','1','2','3','4','5','6','7','8'})
set(gca,'YTick',[1 50 100 150 199],'YTickLabel',{'2','1','0','-1','-2'});
set(gcf,'Position',[500 500 900 390])
set(gca,'Layer','top');
ylabel('y','FontName','Arial', 'FontSize',14);
xlabel('x','FontName','Arial', 'FontSize',14);
axis equal
hold on
% 增加云图控制线
contour(VORT,[linspace(-max(max(VORT)),-max(max(VORT))/35,6)],'-k','LineWidth',1)
contour(VORT,[linspace(max(max(VORT))/35,max(max(VORT)),6)],'--k','LineWidth',1)
theta = (1:100)/100'*2*pi;
x = 49+25*sin(theta);
y = 99+25*cos(theta);
fill(x,y,[.3 .3 .3]) % place cylinder
plot(x,y,'k','LineWidth',1.2) % cylinder boundary
set(gcf,'PaperPositionMode','auto') %
上述两段代码参考hyhhyh21的博文3,内容非常精彩。不愿意跑代码的可以看一下后处理的结果。
流动后处理结果
1,3,5,7,9阶模态分解结果,对应偶数模态为其共轭模态
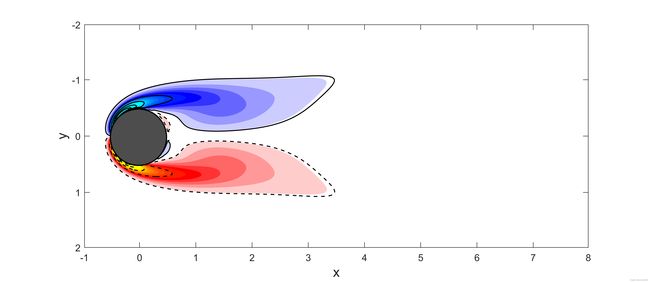
 1阶
1阶
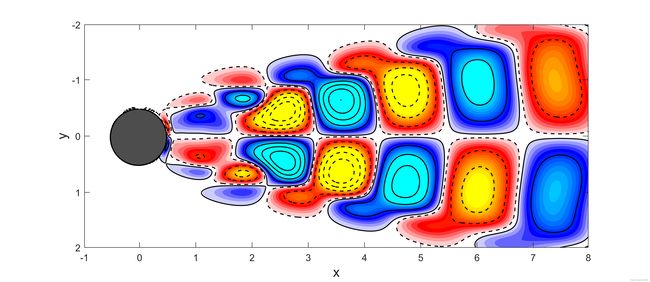
3阶
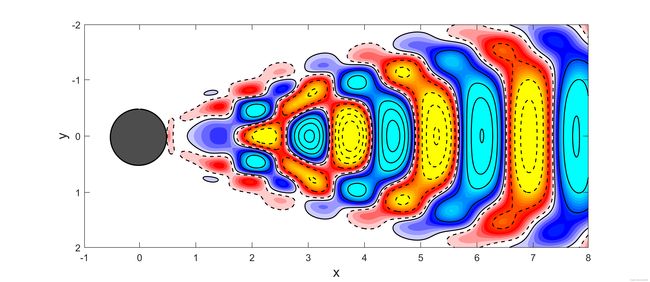 5阶
5阶
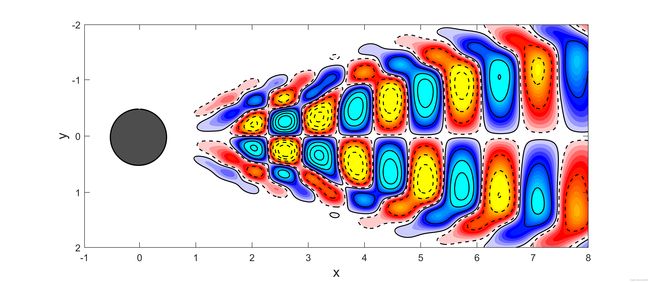 7阶
7阶
9阶
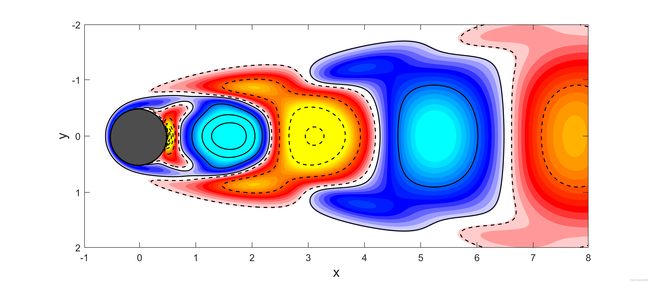
前十阶模态还原瞬态流动
流场还原,可以与原计算流场比较一下,直观上看不出太大区别。
最后送大家一个前十阶模态的功率谱分析,有兴趣的小伙伴可以尝试着做一下
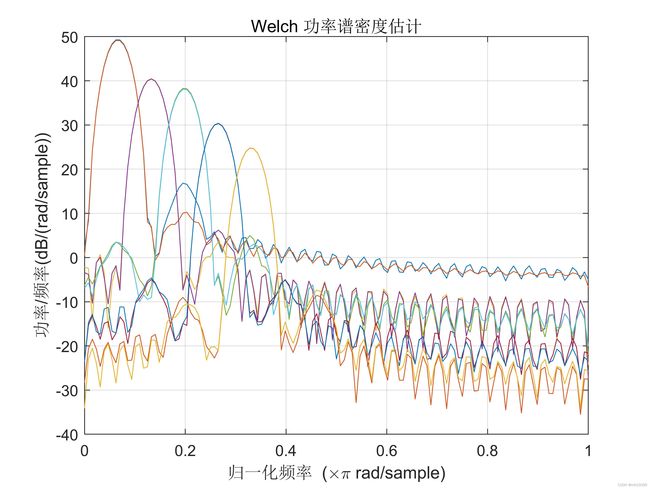 功率谱分析
功率谱分析
本来打算将DMD分析的代码跟结果放在一起,但内容看上去有些多了,还是另起一篇DMD篇,欢迎大家就上述内容进行拍砖,相互交流。
参考文献
J.N. Kutz, S.L. Brunton, B.W. Brunton, J.L. Proctor, Dynamic mode decomposition: data-driven modeling of complex systems, SIAM2016. ↩︎
K. Taira, M.S. Hemati, S.L. Brunton, Y. Sun, K. Duraisamy, S. Bagheri, S.T. Dawson, C.-A. Yeh, Modal analysis of fluid flows: Applications and outlook, AIAA journal, 58 (2020) 998-1022. ↩︎
利用matlab实现POD分解(在一维信号或二维流场矢量中的应用) ↩︎ ↩︎ ↩︎
利用matlab实现DMD动态模态分解(在一维信号或二维流场矢量中的应用) ↩︎ ↩︎