OpenCV实验（8）：基于区域的视觉立体匹配

一. 实验要求

二. 实验思路

1. 想到啥说啥

实验要求参考文献《Obtaining Depth Maps From Color Images By Region Based Stereo Matching Algorithms》，而且实验给的图也是这个论文中的，所以该实验可以看做是对论文的复现。对于这最后一个实验，如果有更好的想法或者发现的问题可以评论或私信我。
继续参考学长的博客https://blog.csdn.net/qq_41748260/article/details/103992462
论文中立体匹配算法的思想直接参考学长的博客就可以了，这里就不重复了。

2. 具体过程

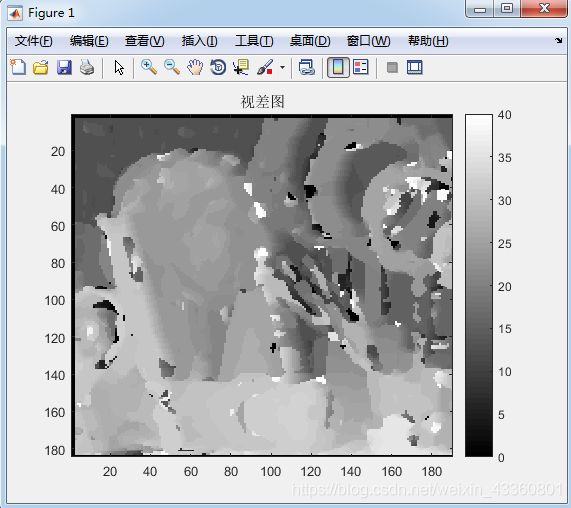
根据"a) Global Error Energy Minimization by Smoothing Functions"，中的steps1、2、3就实现了视差图的计算，再根据"Filtering Unreliable Disparity Estimation By Average Error Thresholding Mechanism"计算具有可靠差异的视差图，接着根据"Depth Map Generation From Disparity Map"，从视差图生成深度图即可。

发现的一些问题和更具体的已经在代码注释中说明了。

三. 实验效果

四. 实验代码

下面这个是完整的代码，代码注释中给出了完整详细的解释

import numpy as np
import cv2 as cv
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
from mpl_toolkits.mplot3d import Axes3D


def disparity_GEEMBSF(imgLeft, imgRight, windowSize=(3, 3), dMax=30, alpha=1):
    """
    论文中的
    "a) Global Error Energy Minimization by Smoothing Functions"
    函数名的命名方式：disparity 表示视差，后面的一串为该方法标题缩写

    :param imgLeft: 左图
    :param imgRight: 右图
    :param windowSize: (n, m)，窗口的尺寸为 n x m
    :param dMax: 中值滤波迭代次数
    :param alpha: 阈值系数
    :return: 视差图，平均误差能量矩阵，函数运行时间
    """
    timeBegin = cv.getTickCount()  # 记录开始时间

    n, m = windowSize  # 窗口大小
    rows, cols, channels = imgLeft.shape  # 该实验中 imgLeft 和 imgRight 的 shape 是一样的，rows=185,cols=231,channels=3
    # 观察到论文中和实验要求中所给的左右原始图是185(行)x231(列)像素的，而结果图中大约是185(行)x190(列)的，
    # 我们的结果中imgDisparity会看到右边缘有大量黑色的区域，如果将其去掉，那么会更美观也会与论文中的结果更加符合
    # 因此在前面我们将cols=190
    cols = 190
    errorEnergyMatrixD = np.zeros((rows, cols, dMax), dtype=np.float)  # 误差能量矩阵（共dMax层），方便后续计算
    errorEnergyMatrixAvgD = np.zeros((rows, cols, dMax), dtype=np.float)  # 平均误差能量矩阵（共dMax层），方便后续计算
    imgDisparity = np.zeros((rows, cols), dtype=np.uint8)  # 具有可靠差异的视差图，将作为结果返回

    # 计算误差能量矩阵 errorEnergyMatrix，平均误差能量矩阵 errorEnergyMatrixAvg
    # 发现的问题：公式(1)在求和计算时，x从i到i+n，y从j到j+m，求和符号是包括上界和下界的，
    # 那么窗口大小就变为了(n+1, m+1)，这与论文中提到的窗口大小为(n, m)是不符的，这一点使我疑惑。
    # 我在处理的时候，计算的是x从i到i+n-1，y从j到j+m-1。

    # 先padding，这样方便使用numpy加速计算
    imgLeftPlus = cv.copyMakeBorder(imgLeft, 0, 0, n-1, m-1+dMax, borderType=cv.BORDER_REPLICATE)
    imgRightPlus = cv.copyMakeBorder(imgRight, 0, 0, n-1, m-1, borderType=cv.BORDER_REPLICATE)
    # 迭代 dMax 次
    for d in range(dMax):
        # 对整个图像进行遍历
        for i in range(rows):
            for j in range(cols):
                # 对于每个 (i, j, d) 根据公式(1)计算误差能量矩阵
                errorEnergy = (imgLeftPlus[i:i+n, j+d:j+m+d, ...] - imgRightPlus[i:i+n, j:j+m, ...]) ** 2
                errorEnergyMatrixD[i, j, d] = np.sum(errorEnergy) / (3 * n * m)
        # 对 errorEnergyMatrix 进行遍历
        for i in range(rows):
            for j in range(cols):
                # 对于每个 (i, j, d) 根据公式(2)计算平均误差能量矩阵
                errorEnergyMatrixAvgD[i, j, d] = np.sum(errorEnergyMatrixD[i:i+n, j:j+m, d]) / (n * m)
        # 论文中说到了（公式(1)下方）
        # For a predetermined disparity
        # search range (w), every e(i, j, d) matrix respect to disparity is smoothed by applying
        # averaging filter many times. (See Figure 1.b)
        # 也就是对于每个e(i, j, d)，进行多次平均滤波。在这里我选择执行3次。
        for k in range(3):
            for i in range(rows):
                for j in range(cols):
                    # 对于每个 (i, j, d) 根据公式(2)计算平均误差能量矩阵
                    # 下面i+n和j+m越了界也是没有问题的，切片会正常计算
                    errorEnergyMatrixAvgD[i, j, d] = np.sum(errorEnergyMatrixAvgD[i:i + n, j:j + m, d]) / (n * m)

    errorEnergyMatrixAvg = np.min(errorEnergyMatrixAvgD, axis=2)  # 平均误差能量矩阵（最终的，只有一层）
    imgDisparity[:, :] = np.argmin(errorEnergyMatrixAvgD, axis=2)  # 视差图
    imgOrignal = imgDisparity.copy()  # 保留一份，并作为结果返回
    # cv.imwrite('../images/out/disparity.png', imgDisparity)

    # cv.imshow('imgDisparity1', imgDisparity)
    # imgDisparityHist = cv.equalizeHist(imgDisparity)  # imgDisparity 太黑了，直方图均衡化方便观察
    # cv.imshow('imgDisparity and imgDisparityHist111', np.hstack([imgDisparity, imgDisparityHist]))  # 水平排列两幅图像进行显示
    # cv.imshow('imgDisparityHistNon', imgDisparityHist)
    # cv.imwrite('../images/out/imgDisparityHist.png', imgDisparityHist)

    # 下面的部分我们实现论文中的：（包含公式 5、6、7、8、9）
    # 可靠差异的视差图
    # "Filtering Unreliable Disparity Estimation By Average Error Thresholding Mechanism"
    Ve = alpha * np.mean(imgDisparity)  # 计算Ve
    temp = errorEnergyMatrixAvg.copy()
    temp[temp > Ve] = 0
    temp[temp != 0] = 1
    temp = temp.astype(np.int)
    imgDisparity = np.multiply(imgDisparity, temp).astype(np.uint8)  # 大于Ve的设置为0
    # Sd = np.sum(temp)  # 计算Sd
    # Rd = 1 / (np.sum(np.multiply(imgDisparity, temp).astype(np.float)) * Sd)  # 计算Rd

    timeEnd = cv.getTickCount()  # 记录结束时间
    time = (timeEnd - timeBegin) / cv.getTickFrequency()  # 计算总时间

    return imgOrignal, imgDisparity, errorEnergyMatrixAvg, time


def depthGeneration(imgDisparity, f=30, T=20):
    """
    实现论文中的"Depth Map Generation From Disparity Map"
    根据视差图，实现深度图

    :param imgDisparity: 具有可靠差异的视差图
    :param f: 焦距
    :param T: 间距
    :return: 深度图
    """
    # 实现公式(4)
    rows, cols = imgDisparity.shape
    imgDepth = np.zeros((rows, cols), dtype=np.uint8)
    for i in range(rows):
        for j in range(cols):
            if imgDisparity[i, j] == 0:
                imgDepth[i, j] = 0
            else:
                imgDepth[i, j] = f * T // imgDisparity[i, j]
    # imgDepthHist = cv.equalizeHist(imgDepth)
    # cv.imshow('imgDepthHist', imgDepthHist)

    return imgDepth


imgLeft = cv.imread('../images/images5/view1m.png')
imgRight = cv.imread('../images/images5/view5m.png')
imgOrignal, imgDisparity, errorEnergyMatrixAvg, time = disparity_GEEMBSF(imgLeft, imgRight)
print(time)  # 打印函数运行时间
imgDepth = depthGeneration(imgDisparity)

# imgDisparityHist = cv.equalizeHist(imgDisparity)  # imgDisparity 太黑了，直方图均衡化方便观察
# cv.imshow('imgDisparityHistReal', imgDisparityHist)

# 下面绘制三幅图像
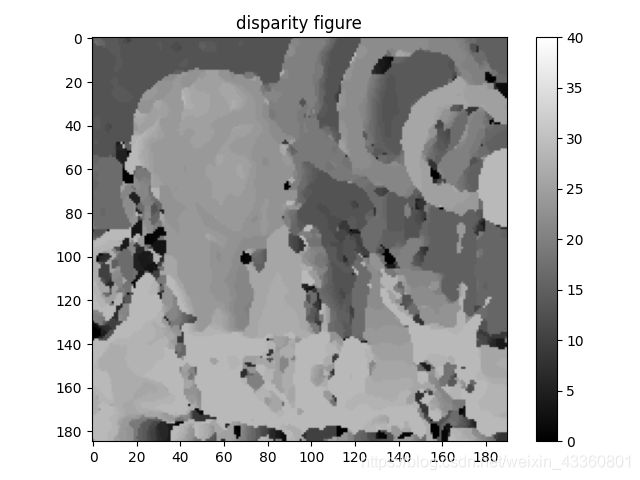
# 视差图图像
plt.figure()
plt.imshow(imgOrignal, cmap='gray', vmin=0, vmax=40)
plt.title('disparity figure')  # 设置标题
ax = plt.gca()  # 返回坐标轴实例
x_major_locator = MultipleLocator(20)  # 刻度间隔为20
y_major_locator = MultipleLocator(20)
ax.xaxis.set_major_locator(x_major_locator)  # 设置坐标间隔
ax.yaxis.set_major_locator(y_major_locator)
plt.colorbar()  # 设置colorBar
plt.show()

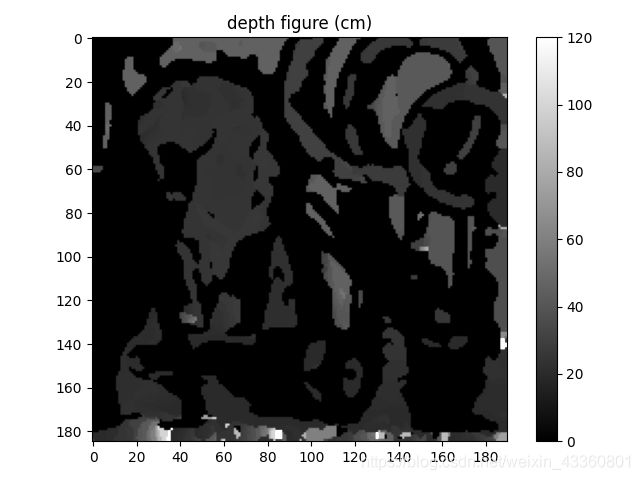
# 深度图图像
plt.figure()
plt.imshow(imgDepth, cmap='gray', vmin=0, vmax=120)
plt.title('depth figure (cm)')  # 设置标题
ax = plt.gca()  # 返回坐标轴实例
x_major_locator = MultipleLocator(20)  # 刻度间隔为20
y_major_locator = MultipleLocator(20)
ax.xaxis.set_major_locator(x_major_locator)  # 设置坐标间隔
ax.yaxis.set_major_locator(y_major_locator)
plt.colorbar()  # 设置colorBar
plt.show()

# 3D图像
# 这里又使我疑惑，实验要求中说是“将深度图用3D视图展示”，但实验结果中3D视图的z轴是0~40也就是视差范围
# 在实验结果中的深度图显示的是cm，所以深度图的3D视图的纵坐标也应该是厘米，而不是视差
# 但为了能和实验结果的图匹配，我将视差图进行了3D展示
fig = plt.figure()
ax = Axes3D(fig)
rows, cols = imgDisparity.shape
x = np.arange(cols)
y = np.arange(rows)
x, y = np.meshgrid(x, y)
z = imgDisparity
surf = ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=plt.get_cmap('gray'),
                       vmin=0, vmax=40)
ax.set_title('3D figure')
ax.set_xlabel('x')
ax.set_ylabel('y')

ax.set_zticks(np.arange(0, 41, 10))
ax.set_xticks(np.arange(0, 185, 30))
ax.set_yticks(np.arange(0, 190, 30))
plt.savefig('3D figure.png', bbox_inches='tight')
plt.show()

cv.waitKey(0)
cv.destroyAllWindows()