【强化学习笔记】4.3 无模型的强化学习方法-蒙特卡罗算法与重要性采样
异策略与重要性采样
因为异策略中的行动策略和目标策略不一样,也就是说行动策略产生的数据分布与目标策略的数据分布存在偏差,即即行动策略的轨迹概率分布和改善策略的轨迹概率分布不一样,因此在使用数据进行目标策略评估的时候需要考虑该影响,常用的方法是重要性采样。(重要性采样的原理见文末图片)
重要性采样评估目标策略的值函数
在目标策略下,一次实验的概率为:
P r ( S t , A t , S t + 1 , . . . S T ) = ∏ k = t T − 1 π ( A k ∣ S k ) p ( S k + 1 ∣ S t , A t ) Pr(S_t,A_t,S_{t+1},...S_T) = \prod _{k=t}^{T-1} \pi(A_k|S_k)p(S_{k+1}|S_t,A_t) Pr(St,At,St+1,...ST)=∏k=tT−1π(Ak∣Sk)p(Sk+1∣St,At)
在行动策略下,该实验出现的概率为:
P r ( S t , A t , S t + 1 , . . . S T ) = ∏ k = t T − 1 μ ( A k ∣ S k ) p ( S k + 1 ∣ S t , A t ) Pr(S_t,A_t,S_{t+1},...S_T) = \prod _{k=t}^{T-1} \mu(A_k|S_k)p(S_{k+1}|S_t,A_t) Pr(St,At,St+1,...ST)=∏k=tT−1μ(Ak∣Sk)p(Sk+1∣St,At)
因为很难获得明确的目标策略 π \pi π的概率分布,因此使用一个替代分布进行估计,对应为行动策略分布 μ \mu μ。因此重要性权重为:
ρ t T = ∏ k = t T − 1 π ( A k ∣ S k ) p ( S k + 1 ∣ S t , A t ) ∏ k = t T − 1 μ ( A k ∣ S k ) p ( S k + 1 ∣ S t , A t ) = ∏ k = t T − 1 π ( A k ∣ S k ) μ ( A k ∣ S k ) \rho _t^T= \frac{\prod _{k=t}^{T-1} \pi(A_k|S_k)p(S_{k+1}|S_t,A_t)}{\prod _{k=t}^{T-1} \mu(A_k|S_k)p(S_{k+1}|S_t,A_t)}=\prod _{k=t}^{T-1} \frac{\pi(A_k|S_k)}{\mu(A_k|S_k)} ρtT=∏k=tT−1μ(Ak∣Sk)p(Sk+1∣St,At)∏k=tT−1π(Ak∣Sk)p(Sk+1∣St,At)=∏k=tT−1μ(Ak∣Sk)π(Ak∣Sk)
普 通 重 要 性 采 样 的 值 函 数 估 计 为 {\color{red}{普通重要性采样的值函数估计为}} 普通重要性采样的值函数估计为:
V ( s ) = ∑ t ∈ T ( s ) ρ t T ( t ) G t ∣ T ( s ) ∣ V(s)= \frac {\sum_{t\in T(s)} \rho_{t}^{T(t)}G_t} {|T(s)|} V(s)=∣T(s)∣∑t∈T(s)ρtT(t)Gt
将上式编程递推的方式:
令 w n = ρ n T ( n ) , ∣ T ( s ) ∣ = n w_n=\rho_{n}^{T(n)},|T(s)|=n wn=ρnT(n),∣T(s)∣=n,那么值函数为
V ( n ) = ∑ k = 1 n − 1 w n G n n V(n)= \frac {\sum_{k=1}^{n-1} w_n G_n} {n} V(n)=n∑k=1n−1wnGn
递推公式很容易获得为:
V ( n + 1 ) = V ( n ) + w n G n − V ( n ) n V(n+1)= V(n) + \frac {w_n G_n - V(n)} {n} V(n+1)=V(n)+nwnGn−V(n)
加 权 重 要 性 采 样 的 值 函 数 为 {\color{red}{加权重要性采样的值函数为}} 加权重要性采样的值函数为:
V ( s ) = ∑ t ∈ T ( s ) ρ t T ( t ) G t ∑ t ∈ T ( s ) ρ t T ( t ) V(s)= \frac {\sum_{t\in T(s)} \rho_{t}^{T(t)}G_t} {\sum_{t\in T(s)} \rho_{t}^{T(t)}} V(s)=∑t∈T(s)ρtT(t)∑t∈T(s)ρtT(t)Gt
令 w n = ρ n T ( n ) , c n = ∑ t ∈ T ( s ) ρ t T ( t ) = c n − 1 + w n w_n=\rho_{n}^{T(n)},c_n=\sum_{t\in T(s)} \rho_{t}^{T(t)}=c_{n-1} + w_n wn=ρnT(n),cn=∑t∈T(s)ρtT(t)=cn−1+wn,那么值函数为
V ( n ) = ∑ k = 1 n − 1 w n G n c n V(n)= \frac {\sum_{k=1}^{n-1} w_n G_n} {c_n} V(n)=cn∑k=1n−1wnGn
递推公式很容易获得为:
V ( n + 1 ) = V ( n ) + w n c n ( G n − V ( n ) ) V(n+1)= V(n) + \frac {w_n} {c_n} (G_n - V(n)) V(n+1)=V(n)+cnwn(Gn−V(n))
代码实现【强化学习笔记】4.4 无模型的强化学习方法-蒙特卡罗算法与重要性采样代码实现
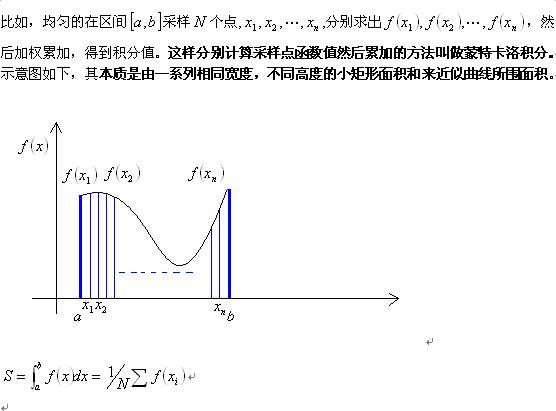
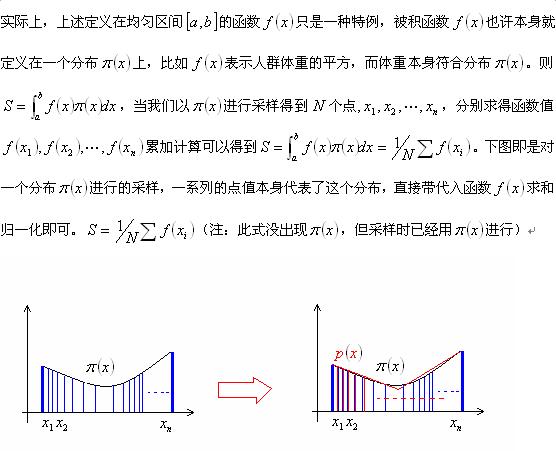
重要性采样(转载https://blog.csdn.net/minenki/article/details/8917520)
参考书籍:
- 深入浅出强化学习原理入门
欢迎关注微信公众号:AITBOOK
![]()