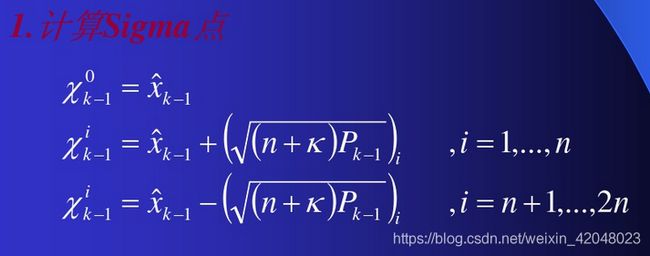HDL-localization源码阅读

最近在回顾自己的人生（误），至少也是一个阶段性的总结，发现定位这一块虽然也做过一点但是一直没钻得很深。对于低速运动来说，将demo进行魔改后在95%的情况下也够用，另外的额外选择就是加入视觉定位，即每一次建图或者定位都将第一帧的坐标系转移到地图坐标系下，重新做一次视觉slam，用视觉里程计加入robot-pose-ekf里面进行估计。不过，之前的技术方案是针对三维激光雷达做的，在更常见的二维激光定位中，amcl是用得最多的方法，粒子滤波可以最大程度地拟合状态量的概率分布，这也衍生出3d-mcl的多线雷达的定位方法。

对于我的16线雷达，我使用的是hdl-localization，它用的是ndt匹配加上UKF的数据融合，这不禁想到了MSCKF系列中的视觉约束与速度先验的融合，以及EKF-SLAM中二维码路标和轮式里程计的校验，其实在滤波框架下都是殊途同归的。它的新颖之处在于后端数据融合使用的UKF，与EKF相比较，UKF更好地拟合非线性的概率分布，而不是强行进行线性化，EKF由于要计算雅可比矩阵，更烧脑一些，UKF要对协方差矩阵做开方，也需要用到矩阵分解，两者计算量差不多。当然，如果一定要用EKF应该也能解决如今的低速定位问题。

在hdl中使用的ndt就像我们熟悉的pcl接口一样，只不过调用了多线程omp模式，它提供的是测量值。imu提供的是先验值，我们如果选择不用imu则先验值为原有的位姿。

参与融合的状态向量依然是p、v、q、ba、bg，一共16维，观测量则是7维，即p、q。和其它KF的接口一样，这里提供了predict和correct两个接口：

1.更新预测

control是传入的一帧imu数据，我们姑且看作是控制量，预测时首先判断协方差矩阵是否是方阵并且是否正定，因为我们在求sigma点的过程中要求协方差矩阵的逆，因此提取出它们的特征值和特征向量并再次相乘。接下来就是求解sigma点了：

直接盗用https://wenku.baidu.com/view/27bfa8a442323968011ca300a6c30c225901f08f.html#的图。。。在这里K是可调整的参数。

void computeSigmaPoints(const VectorXt& mean, const MatrixXt& cov, MatrixXt& sigma_points) {
    const int n = mean.size();
    assert(cov.rows() == n && cov.cols() == n);
    //用llt分解求协方差的逆矩阵
    Eigen::LLT llt;
    llt.compute((n + lambda) * cov);
    MatrixXt l = llt.matrixL();

    sigma_points.row(0) = mean;
    for (int i = 0; i < n; i++) {
      sigma_points.row(1 + i * 2) = mean + l.col(i);
      sigma_points.row(1 + i * 2 + 1) = mean - l.col(i);
    }
  }

 在计算到所有的sigma点之后，用这些点重新拟合一个正态分布，在这个过程中引入了权重weights，它的初始赋值在构造函数中：

weights[0] = lambda / (N + lambda);
    for (int i = 1; i < 2 * N + 1; i++) {
      weights[i] = 1 / (2 * (N + lambda));
    }

  void predict(const VectorXt& control) 
  {
    // calculate sigma points
    ensurePositiveFinite(cov);
    computeSigmaPoints(mean, cov, sigma_points);
    for (int i = 0; i < S; i++) {
      //状态转移方程
      sigma_points.row(i) = system.f(sigma_points.row(i), control);
    }

    const auto& R = process_noise;

    // unscented transform
    VectorXt mean_pred(mean.size());
    MatrixXt cov_pred(cov.rows(), cov.cols());

    mean_pred.setZero();
    cov_pred.setZero();
    for (int i = 0; i < S; i++) {
      mean_pred += weights[i] * sigma_points.row(i);
    }
    for (int i = 0; i < S; i++) {
      VectorXt diff = sigma_points.row(i).transpose() - mean_pred;
      cov_pred += weights[i] * diff * diff.transpose();
    }
    cov_pred += R;

    mean = mean_pred;
    cov = cov_pred;
  }

在每帧imu传入后都进行一次预测更新，在观测矫正之前我们得到了sigma点拟合的状态分布，而非状态转换矩阵，很像粒子滤波。

2.观测值估计真值

correct函数是观测矫正的过程，我们先拟合观测的sigma点，再用观测方程求解观测的均值，并加权计算扩增后的预测状态以及观测状态的协方差矩阵。

void correct(const VectorXt& measurement) 
  {
    // create extended state space which includes error variances
    //状态扩增，即先更新预测值的协方差矩阵，将上一部分用sigma点拟合的协方差加上测量噪声
    VectorXt ext_mean_pred = VectorXt::Zero(N + K, 1);
    MatrixXt ext_cov_pred = MatrixXt::Zero(N + K, N + K);
    ext_mean_pred.topLeftCorner(N, 1) = VectorXt(mean);
    ext_cov_pred.topLeftCorner(N, N) = MatrixXt(cov);
    ext_cov_pred.bottomRightCorner(K, K) = measurement_noise;
    //拟合状态扩增后的均值与协方差，也就是再算一遍sigma点
    ensurePositiveFinite(ext_cov_pred);
    computeSigmaPoints(ext_mean_pred, ext_cov_pred, ext_sigma_points);

    // unscented transform
    //UT变换，即拟合测量的均值和协方差
    expected_measurements.setZero();
    for (int i = 0; i < ext_sigma_points.rows(); i++) {
      expected_measurements.row(i) = system.h(ext_sigma_points.row(i).transpose().topLeftCorner(N, 1));
      expected_measurements.row(i) += VectorXt(ext_sigma_points.row(i).transpose().bottomRightCorner(K, 1));
    }
    //虽然叫expected，但这是7维的测量值，也就是用sigma点拟合的测量分布！
    VectorXt expected_measurement_mean = VectorXt::Zero(K);
    for (int i = 0; i < ext_sigma_points.rows(); i++) {
      expected_measurement_mean += ext_weights[i] * expected_measurements.row(i);
    }
    //测量的协方差矩阵，即Pk+1
    MatrixXt expected_measurement_cov = MatrixXt::Zero(K, K);
    for (int i = 0; i < ext_sigma_points.rows(); i++) {
      VectorXt diff = expected_measurements.row(i).transpose() - expected_measurement_mean;
      expected_measurement_cov += ext_weights[i] * diff * diff.transpose();
    }

    // calculated transformed covariance
    //那么，在这里的23*7的sigma矩阵就是状态扩增后的Pk|k+1
    MatrixXt sigma = MatrixXt::Zero(N + K, K);
    for (int i = 0; i < ext_sigma_points.rows(); i++) {
      auto diffA = (ext_sigma_points.row(i).transpose() - ext_mean_pred);
      auto diffB = (expected_measurements.row(i).transpose() - expected_measurement_mean);
      sigma += ext_weights[i] * (diffA * diffB.transpose());
    }
    //计算卡尔曼增益K=Pk|k+1/Pk
    kalman_gain = sigma * expected_measurement_cov.inverse();
    const auto& K = kalman_gain;
    //更新观测后的真值估计
    VectorXt ext_mean = ext_mean_pred + K * (measurement - expected_measurement_mean);
    MatrixXt ext_cov = ext_cov_pred - K * expected_measurement_cov * K.transpose();

    mean = ext_mean.topLeftCorner(N, 1);
    cov = ext_cov.topLeftCorner(N, N);
  }

最后简单总结一下UKF的过程：

1.产生2n+1个sigma点，在状态向量的附近，有点像粒子滤波。

2.利用状态转移矩阵，预测观测量的sigma点，并根据权重计算状态向量的均值和协方差矩阵。

3.利用测量矩阵得到sigma点的预测测量值。

4.根据sigma点和权重得到状态向量的预测值。

5.根据KF公式，将状态向量的预测值和观测值进行真值估计。

因此hdl的逻辑就很清晰地显示出来了，在获取到估计值后，便将状态向量的前10维，也就是pvq取出得到位姿的估计值，实现了定位的迭代。

  Eigen::Vector3f pos() const {
    return Eigen::Vector3f(ukf->mean[0], ukf->mean[1], ukf->mean[2]);
  }

  Eigen::Vector3f vel() const {
    return Eigen::Vector3f(ukf->mean[3], ukf->mean[4], ukf->mean[5]);
  }

  Eigen::Quaternionf quat() const {
    return Eigen::Quaternionf(ukf->mean[6], ukf->mean[7], ukf->mean[8], ukf->mean[9]).normalized();
  }

  Eigen::Matrix4f matrix() const {
    Eigen::Matrix4f m = Eigen::Matrix4f::Identity();
    m.block<3, 3>(0, 0) = quat().toRotationMatrix();
    m.block<3, 1>(0, 3) = pos();
    return m;
  }