2021-06-16 Datawhale GNN组队学习--Task01
@[Datawhale GNN组队学习——Task02]
推荐系统中的图结构数据
推荐系统中的涉及到的对象(user、item、feature等)大多数显式或隐式连接,构成天然的图并互相影响。基于图的推荐系统(GLRS)考虑到对象间的复杂关系,不仅可以丰富对象表示,还可以借助图推理提升推荐系统的可解释性。
如何考虑不同的图结构的信息,为推荐系统带来了不同的挑战:
- 树状图(item层次图):item间具有层次关系。同层不同类的相邻item可能具有互补性(配套使用),同类item可能具有替代性(应避免重复推荐)。如何学习item间的层次关系存在挑战。
- 不可分割图:指user社交图和item共现图(如,同一购物篮),前者反映user间的社交影响,后者反映item间的某种潜在关系(替代/互补/用户的购物模式等)。如何学习user-user间、item-item间的相互影响存在挑战。
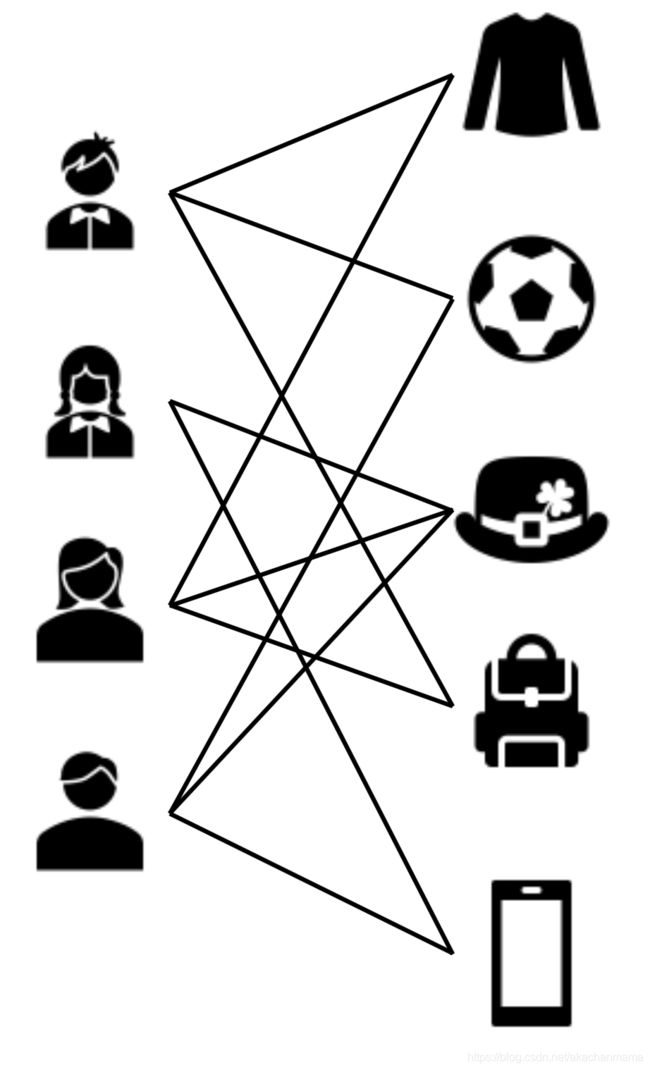
- 二分图(user-item图):是推荐系统的核心(基本组件)。交互类型可能单一或多种,推荐可以看作user-item图上的链接预测。如何考虑图上不同类型的user-item交互之间的影响及其综合影响,存在挑战。
- 属性图:这里强调user/item在属性图/特征图(如kNN图,而非社交/共现图)上的相似性。如何在推荐系统中建模属性图,以及item-attribute构成的异质图,存在挑战。
- 复杂异构图:二分图和不可分割图同时出现,形成异构图。如何结合二分图与不可分割图上的信息,使来自两个图的异构信息能够适当地相互通信存在挑战。
- 多源异构图:多个不同来源的图,信息可能互相补充,有助于解决数据稀疏性和冷启动问题,但也可能存在噪声和矛盾之处。如何结合多源异构图存在挑战。
不同的图学习方法,可以解决上面的挑战:
- 随机游走:可以捕获图上各类实体的高阶关系、交互传播、隐式偏好等建模,缺点是效率低,且缺乏用于优化推荐目标的模型参数。
- 图表示学习:学习user/item的低维表示。根据算法原理不同,可分为三类:基于矩阵分解的模型(优点:快、简单、适用于数据稀疏场景)、基于skip-gram的模型(优点:简单、高效)和基于GNN的模型(优点:容易和其他下游推荐模型集成,端到端训练,方便优化)。
- 图神经网络:这里列举了三类,分别是图注意力网络、门控图神经网络和图卷积网络。(除了视为图表示学习方法,GNN在建模复杂关系、提升可解释性等方面也有帮助。)
- 知识图谱:通常作为外部知识库出现,这里主要关注KG的构建,而不是如何从已构建的KG中提取信息(第一篇重点讨论的)。KG构建可以分为三类:基于本体的KGRS(树状图,表示归属关系),基于辅助信息的KGRS(属性图,表示特征级隐式连接)和基于常识的KGRS(如,领域知识外的一般语义,解决多源异构问题)。
参考论文:[[Graph Learning Approaches to Recommender Systems: A Review]] Shoujin Wang, Liang Hu, Yan Wang, Xiangnan He, etc.
图论
一、图的表示
定义一(图):
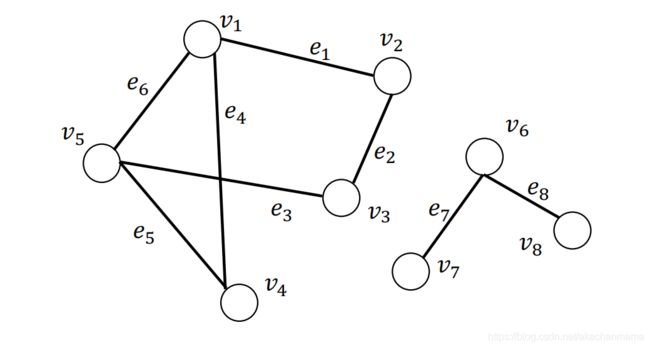
- 一个图被记为 G = { V , E } \mathcal{G}=\{\mathcal{V}, \mathcal{E}\} G={V,E},其中 V = { v 1 , … , v N } \mathcal{V}=\left\{v_{1}, \ldots, v_{N}\right\} V={v1,…,vN}是数量为 N = ∣ V ∣ N=|\mathcal{V}| N=∣V∣ 的节点的集合, E = { e 1 , … , e M } \mathcal{E}=\left\{e_{1}, \ldots, e_{M}\right\} E={e1,…,eM} 是数量为 M M M 的边的集合。
- 图用节点表示实体(entities ),用边表示实体间的关系(relations)。注:所以[[知识图谱]]是典型的的图结构数据
- 节点和边的信息可以是类别型的(categorical),类别型数据的取值只能是哪一类别。一般称类别型的信息为标签(label)。
- 节点和边的信息可以是数值型的(numeric),数值型数据的取值范围为实数。一般称数值型的信息为属性(attribute)。
- 在图的计算任务中,我们认为,节点一定含有信息(至少含有节点的度的信息),边可能含有信息。
定义二(图的邻接矩阵):
-
给定一个图 G = { V , E } \mathcal{G}=\{\mathcal{V}, \mathcal{E}\} G={V,E},其对应的邻接矩阵被记为 A ∈ { 0 , 1 } N × N \mathbf{A} \in\{0,1\}^{N \times N} A∈{0,1}N×N。 A i , j = 1 \mathbf{A}_{i, j}=1 Ai,j=1表示存在从节点 v i v_i vi到 v j v_j vj的边,反之表示不存在从节点 v i v_i vi到 v j v_j vj的边。
-
在无向图中,从节点 v i v_i vi到 v j v_j vj的边存在,意味着从节点 v j v_j vj到 v i v_i vi的边也存在。因而无向图的邻接矩阵是对称的。
-
在无权图中,各条边的权重被认为是等价的,即认为各条边的权重为 1 1 1。
-
对于有权图,其对应的邻接矩阵通常被记为 W ∈ { 0 , 1 } N × N \mathbf{W} \in\{0,1\}^{N \times N} W∈{0,1}N×N,其中 W i , j = w i j \mathbf{W}_{i, j}=w_{ij} Wi,j=wij表示从节点 v i v_i vi到 v j v_j vj的边的权重。若边不存在时,边的权重为 0 0 0。
其邻接矩阵为:
A = ( 0 1 0 1 1 1 0 1 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 1 0 ) \mathbf{A}=\left(\begin{array}{lllll} 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 \end{array}\right) A=⎝⎜⎜⎜⎜⎛0101110100010011000110110⎠⎟⎟⎟⎟⎞
二、图的属性
定义三(节点的度,degree):
- 对于有向有权图,节点 v i v_i vi的出度(out degree)等于从 v i v_i vi出发的边的权重之和,节点 v i v_i vi的入度(in degree)等于从连向 v i v_i vi的边的权重之和。
- 无向图是有向图的特殊情况,节点的出度与入度相等。
- 无权图是有权图的特殊情况,各边的权重为 1 1 1,那么节点 v i v_i vi的出度(out degree)等于从 v i v_i vi出发的边的数量,节点 v i v_i vi的入度(in degree)等于从连向 v i v_i vi的边的数量。
- 节点 v i v_i vi的度记为 d ( v i ) d(v_i) d(vi),入度记为 d i n ( v i ) d_{in}(v_i) din(vi),出度记为 d o u t ( v i ) d_{out}(v_i) dout(vi)。
定义四(邻接节点,neighbors):
- 节点 v i v_i vi的邻接节点为与节点 v i v_i vi直接相连的节点,其被记为** N ( v i ) \mathcal{N(v_i)} N(vi)**。
- **节点 v i v_i vi的 k k k跳远的邻接节点(neighbors with k k k-hop)**指的是到节点 v i v_i vi要走 k k k步的节点(一个节点的 2 2 2跳远的邻接节点包含了自身)。
定义五(行走,walk):
- w a l k ( v 1 , v 2 ) = ( v 1 , e 6 , e 5 , e 4 , e 1 , v 2 ) walk(v_1, v_2) = (v_1, e_6,e_5,e_4,e_1,v_2) walk(v1,v2)=(v1,e6,e5,e4,e1,v2),这是一次“行走”,它是一次从节点 v 1 v_1 v1出发,依次经过边 e 6 , e 5 , e 4 , e 1 e_6,e_5,e_4,e_1 e6,e5,e4,e1,最终到达节点 v 2 v_2 v2的“行走”。
- 下图所示为 w a l k ( v 1 , v 2 ) = ( v 1 , e 6 , e 5 , e 4 , e 1 , v 2 ) walk(v_1, v_2) = (v_1, e_6,e_5,e_4,e_1,v_2) walk(v1,v2)=(v1,e6,e5,e4,e1,v2),其中红色数字标识了边的访问序号。
- 在“行走”中,节点是允许重复的。
==定理六:
- 有一图,其邻接矩阵为 A \mathbf{A} A, A n \mathbf{A}^{n} An为邻接矩阵的 n n n次方,那么 A n [ i , j ] \mathbf{A}^{n}[i,j] An[i,j]等于从节点 v i v_i vi到节点 v j v_j vj的长度为 n n n的行走的个数。(也就是,以节点 v i v_i vi为起点,节点 v j v_j vj为终点,长度为 n n n的节点访问方案的数量,节点访问中可以兜圈子重复访问一些节点)
定义七(路径,path):
- “路径”是节点不可重复的“行走”。
定义八(子图,subgraph):
- 有一图 G = { V , E } \mathcal{G}=\{\mathcal{V}, \mathcal{E}\} G={V,E},另有一图 G ′ = { V ′ , E ′ } \mathcal{G}^{\prime}=\{\mathcal{V}^{\prime}, \mathcal{E}^{\prime}\} G′={V′,E′},其中 V ′ ∈ V \mathcal{V}^{\prime} \in \mathcal{V} V′∈V, E ′ ∈ E \mathcal{E}^{\prime} \in \mathcal{E} E′∈E并且 V ′ \mathcal{V}^{\prime} V′不包含 E ′ \mathcal{E}^{\prime} E′中未出现过的节点,那么 G ′ \mathcal{G}^{\prime} G′是 G \mathcal{G} G的子图。
定义九(连通分量,connected component):
- 给定图 G ′ = { V ′ , E ′ } \mathcal{G}^{\prime}=\{\mathcal{V}^{\prime}, \mathcal{E}^{\prime}\} G′={V′,E′}是图 G = { V , E } \mathcal{G}=\{\mathcal{V}, \mathcal{E}\} G={V,E}的子图。记属于图 G \mathcal{G} G但不属于 G ′ \mathcal{G}^{\prime} G′图的节点集合记为 V / V ′ \mathcal{V}/\mathcal{V}^{\prime} V/V′ 。如果属于 V ′ \mathcal{V}^{\prime} V′的任意节点对之间存在至少一条路径,但不存在一条边连接属于 V ′ \mathcal{V}^{\prime} V′的节点与属于 V / V ′ \mathcal{V}/\mathcal{V}^{\prime} V/V′的节点,那么图 G ′ \mathcal{G}^{\prime} G′是图 G \mathcal{G} G的连通分量。
左右两边子图都是整图的连通分量。
定义十(连通图,connected graph):
- 当一个图只包含一个连通分量,即其自身,那么该图是一个连通图。
定义十一(最短路径,shortest path):
- v s , v t ∈ V v_{s}, v_{t} \in \mathcal{V} vs,vt∈V 是图 G = { V , E } \mathcal{G}=\{\mathcal{V}, \mathcal{E}\} G={V,E}上的一对节点,节点对 v s , v t ∈ V v_{s}, v_{t} \in \mathcal{V} vs,vt∈V之间所有路径的集合记为 P s t \mathcal{P}_{\mathrm{st}} Pst。节点对 v s , v t v_{s}, v_{t} vs,vt之间的最短路径 p s t s p p_{\mathrm{s} t}^{\mathrm{sp}} pstsp为 P s t \mathcal{P}_{\mathrm{st}} Pst中长度最短的一条路径,其形式化定义为
p s t s p = arg min p ∈ P s t ∣ p ∣ p_{\mathrm{s} t}^{\mathrm{sp}}=\arg \min _{p \in \mathcal{P}_{\mathrm{st}}}|p| pstsp=argp∈Pstmin∣p∣
其中, p p p表示 P s t \mathcal{P}_{\mathrm{st}} Pst中的一条路径, ∣ p ∣ |p| ∣p∣是路径 p p p的长度。
定义十二(直径,diameter):
- 给定一个连通图 G = { V , E } \mathcal{G}=\{\mathcal{V}, \mathcal{E}\} G={V,E},其直径为其所有节点对之间的最短路径的最大值,形式化定义为
diameter ( G ) = max v s , v t ∈ V min p ∈ P s t ∣ p ∣ \operatorname{diameter}(\mathcal{G})=\max _{v_{s}, v_{t} \in \mathcal{V}} \min _{p \in \mathcal{P}_{s t}}|p| diameter(G)=vs,vt∈Vmaxp∈Pstmin∣p∣
定义十三(拉普拉斯矩阵,Laplacian Matrix):
- 给定一个图 G = { V , E } \mathcal{G}=\{\mathcal{V}, \mathcal{E}\} G={V,E},其邻接矩阵为 A A A,其拉普拉斯矩阵定义为 L = D − A \mathbf{L=D-A} L=D−A,其中 D = d i a g ( d ( v 1 ) , ⋯ , d ( v N ) ) \mathbf{D=diag(d(v_1), \cdots, d(v_N))} D=diag(d(v1),⋯,d(vN))。
定义十四(对称归一化的拉普拉斯矩阵,Symmetric normalized Laplacian):
- 给定一个图 G = { V , E } \mathcal{G}=\{\mathcal{V}, \mathcal{E}\} G={V,E},其邻接矩阵为 A A A,其规范化的拉普拉斯矩阵定义为
L = D − 1 2 ( D − A ) D − 1 2 = I − D − 1 2 A D − 1 2 \mathbf{L=D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}} L=D−21(D−A)D−21=I−D−21AD−21
- 这里的-1/2是矩阵的二分之一次方再取逆。D是度矩阵,是一个对角矩阵,对角上的元素为各顶点的度。I是单位矩阵。
- 为什么要归一化:采用加法规则时,对于度大的节点特征越来越大,而对于度小的节点却相反,这可能导致网络训练过程中梯度爆炸或者消失的问题。
三、图的种类
-
同质图(Homogeneous Graph):只有一种类型的节点和一种类型的边的图。
四、图结构数据上的机器学习
- 节点预测:预测节点的类别或某类属性的取值
- 例子:对是否是潜在客户分类、对游戏玩家的消费能力做预测
- 边预测:预测两个节点间是否存在链接
- 例子:Knowledge graph completion、好友推荐、商品推荐
- 图的预测:对不同的图进行分类或预测图的属性
- 例子:分子属性预测
- 节点聚类:检测节点是否形成一个社区
- 例子:社交圈检测
- 其他任务
- 图生成:例如药物发现
- 图演变:例如物理模拟
- ……
五、应用神经网络于图面临的挑战
在学习了简单的图论知识,我们再来回顾应用神经网络于图面临的挑战。
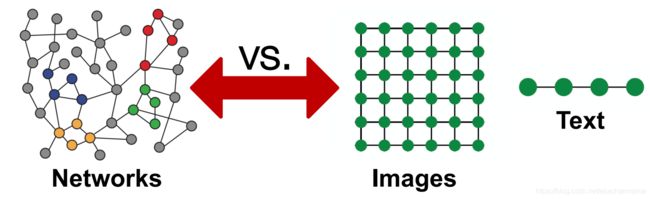
过去的深度学习应用中,我们主要接触的数据形式主要是这四种:矩阵、张量、序列(sequence)和时间序列(time series),它们都是规则的结构化的数据。然而图数据是非规则的非结构化的,它具有以下的特点:
- 任意的大小和复杂的拓扑结构;
- 没有固定的节点排序或参考点;
- 通常是动态的,并具有多模态的特征;
- 图的信息并非只蕴含在节点信息和边的信息中,图的信息还包括了图的拓扑结构。
以往的深度学习技术是为规则且结构化的数据设计的,无法直接用于图数据。应用于图数据的神经网络,要求
- 适用于不同度的节点;
- 节点表征的计算与邻接节点的排序无关;
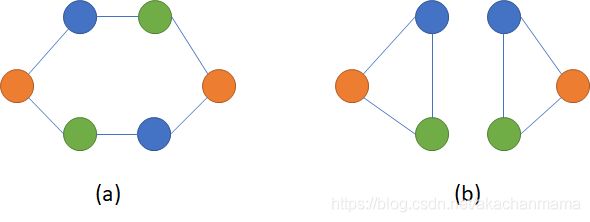
- 不但能够根据节点信息、邻接节点的信息和边的信息计算节点表征,还能根据图拓扑结构计算节点表征。下面的图片展示了一个需要根据图拓扑结构计算节点表征的例子。图片中展示了两个图,它们同样有俩黄、俩蓝、俩绿,共6个节点,因此它们的节点信息相同;假设边两端节点的信息为边的信息,那么这两个图有一样的边,即它们的边信息相同。但这两个图是不一样的图,它们的拓扑结构不一样。
参考资料
- Chapter 2 - Foundations of Graphs, Deep Learning on Graphs
- Datawhale GNN 组队学习资料
环境配置与PyG中图与图数据集的表示和使用
一、PyG简介
PyTorch Geometric (PyG)是面向几何深度学习的PyTorch的扩展库,几何深度学习指的是应用于图和其他不规则、非结构化数据的深度学习。基于PyG库,我们可以轻松地根据数据生成一个图对象,然后很方便的使用它;我们也可以容易地为一个图数据集构造一个数据集类,然后很方便的将它用于神经网络。
二、环境配置
-
==我自己的机器是Mac OS系统,intel显卡,没有独显,所以只能用CPU算力。只要安装pytorch就行,装不了cudatoolkit。
-
安装正确版本的pytorch,此处安装1.8.1版本的pytorch(查看pytorch官网,选择自己机器的配置就可以看到安装命令行)
conda install pytorch torchvision torchaudio -c pytorch- 确认是否正确安装,正确的安装应出现下方的结果
$ python -c "import torch; print(torch.__version__)" # 1.8.1 -
安装正确版本的PyG
pip install torch-scatter -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html pip install torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html pip install torch-cluster -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html pip install torch-spline-conv -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html pip install torch-geometric
其他版本的安装方法以及安装过程中出现的大部分问题的解决方案可以在Installation of of PyTorch Geometric 页面找到。
三、快速上手Data类
import torch from torch_geometric.data import Data
#边,shape = [2,num_edge]
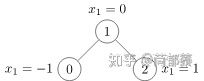
edge_index = torch.tensor([[0, 1, 1, 2], [1, 0, 2, 1]], dtype=torch.long)
#点,shape = [num_nodes, num_node_features]
x = torch.tensor([[-1], [0], [1]], dtype=torch.float)
data = Data(x=x, edge_index=edge_index)
>>> Data(edge_index=[2, 4], x=[3, 1])
Data对象的创建
Data类的官方文档为torch_geometric.data.Data。
通过构造函数
Data类的构造函数:
class Data(object):
def __init__(self, x=None, edge_index=None, edge_attr=None, y=None, **kwargs):
r"""
Args:
x (Tensor, optional): 节点属性矩阵,大小为`[num_nodes, num_node_features]`
edge_index (LongTensor, optional): 边索引矩阵,大小为`[2, num_edges]`,第0行为尾节点,第1行为头节点,头指向尾
edge_attr (Tensor, optional): 边属性矩阵,大小为`[num_edges, num_edge_features]`
y (Tensor, optional): 节点或图的标签,任意大小(,其实也可以是边的标签)
"""
self.x = x
self.edge_index = edge_index
self.edge_attr = edge_attr
self.y = y
for key, item in kwargs.items():
if key == 'num_nodes':
self.__num_nodes__ = item
else:
self[key] = item
edge_index的每一列定义一条边,其中第一行为边起始节点的索引,第二行为边结束节点的索引。这种表示方法被称为COO格式(coordinate format),通常用于表示稀疏矩阵。PyG不是用稠密矩阵 A ∈ { 0 , 1 } ∣ V ∣ × ∣ V ∣ \mathbf{A} \in \{ 0, 1 \}^{|\mathcal{V}| \times |\mathcal{V}|} A∈{0,1}∣V∣×∣V∣来持有邻接矩阵的信息,而是用仅存储邻接矩阵 A \mathbf{A} A中非 0 0 0元素的稀疏矩阵来表示图。
通常,一个图至少包含x, edge_index, edge_attr, y, num_nodes5个属性,当图包含其他属性时,我们可以通过指定额外的参数使Data对象包含其他的属性:
graph = Data(x=x, edge_index=edge_index, edge_attr=edge_attr, y=y, num_nodes=num_nodes, other_attr=other_attr)
转dict对象为Data对象
我们也可以将一个dict对象转换为一个Data对象:
graph_dict = {
'x': x,
'edge_index': edge_index,
'edge_attr': edge_attr,
'y': y,
'num_nodes': num_nodes,
'other_attr': other_attr
}
graph_data = Data.from_dict(graph_dict)
from_dict是一个类方法:
@classmethod
def from_dict(cls, dictionary):
r"""Creates a data object from a python dictionary."""
data = cls()
for key, item in dictionary.items():
data[key] = item
return data
注意:graph_dict中属性值的类型与大小的要求与Data类的构造函数的要求相同。
Data对象转换成其他类型数据
我们可以将Data对象转换为dict对象:
def to_dict(self):
return {key: item for key, item in self}
或转换为namedtuple:
def to_namedtuple(self):
keys = self.keys
DataTuple = collections.namedtuple('DataTuple', keys)
return DataTuple(*[self[key] for key in keys])
获取Data对象属性
x = graph_data['x']
设置Data对象属性
graph_data['x'] = x
获取Data对象包含的属性的关键字
graph_data.keys()
对边排序并移除重复的边
graph_data.coalesce()
Data对象的其他性质
我们通过观察PyG中内置的一个图来查看Data对象的性质:
from torch_geometric.datasets import KarateClub
dataset = KarateClub()
data = dataset[0] # Get the first graph object.
print(data)
print('==============================================================')
# 获取图的一些信息
print(f'Number of nodes: {data.num_nodes}') # 节点数量
print(f'Number of edges: {data.num_edges}') # 边数量
print(f'Number of node features: {data.num_node_features}') # 节点属性的维度
print(f'Number of node features: {data.num_features}') # 同样是节点属性的维度
print(f'Number of edge features: {data.num_edge_features}') # 边属性的维度
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}') # 平均节点度
print(f'if edge indices are ordered and do not contain duplicate entries.: {data.is_coalesced()}') # 是否边是有序的同时不含有重复的边
print(f'Number of training nodes: {data.train_mask.sum()}') # 用作训练集的节点
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}') # 用作训练集的节点数占比
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}') # 此图是否包含孤立的节点
print(f'Contains self-loops: {data.contains_self_loops()}') # 此图是否包含自环的边
print(f'Is undirected: {data.is_undirected()}') # 此图是否是无向图
四、Dataset类——PyG中图数据集的表示及其使用
PyTorch Geometric已经包含有很多常见的基准数据集,包括:
- Cora:一个根据科学论文之间相互引用关系而构建的Graph数据集合,论文分为7类:Genetic_Algorithms,Neural_Networks,Probabilistic_Methods,Reinforcement_Learning,Rule_Learning,Theory,共2708篇;
- Citeseer:一个论文之间引用信息数据集,论文分为6类:Agents、AI、DB、IR、ML和HCI,共包含3312篇论文;
- Pubmed:生物医学方面的论文搜寻以及摘要数据集。
以及网址中的数据集等等。
接下来我们以PyG内置的Planetoid数据集为例,来学习PyG中图数据集的表示及使用。
Planetoid数据集类的官方文档为torch_geometric.datasets.Planetoid。
生成数据集对象并分析数据集
如下方代码所示,在PyG中生成一个数据集是简单直接的。在第一次生成PyG内置的数据集时,程序首先下载原始文件,然后将原始文件处理成包含Data对象的Dataset对象并保存到文件。
from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='/dataset/Cora', name='Cora')
# Cora()
len(dataset)
# 1
dataset.num_classes
# 7
dataset.num_node_features
# 1433
分析数据集中样本
可以看到该数据集只有一个图,包含7个分类任务,节点的属性为1433维度。
data = dataset[0]
# Data(edge_index=[2, 10556], test_mask=[2708],
# train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708])
data.is_undirected()
# True
data.train_mask.sum().item()
# 140
data.val_mask.sum().item()
# 500
data.test_mask.sum().item()
# 1000
现在我们看到该数据集包含的唯一的图,有2708个节点,节点特征为1433维,有10556条边,有140个用作训练集的节点,有500个用作验证集的节点,有1000个用作测试集的节点。PyG内置的其他数据集,请小伙伴一一试验,以观察不同数据集的不同。
数据集的使用
假设我们定义好了一个图神经网络模型,其名为Net。在下方的代码中,我们展示了节点分类图数据集在训练过程中的使用。
model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)
model.train()
for epoch in range(200):
optimizer.zero_grad()
out = model(data)
loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()
作业
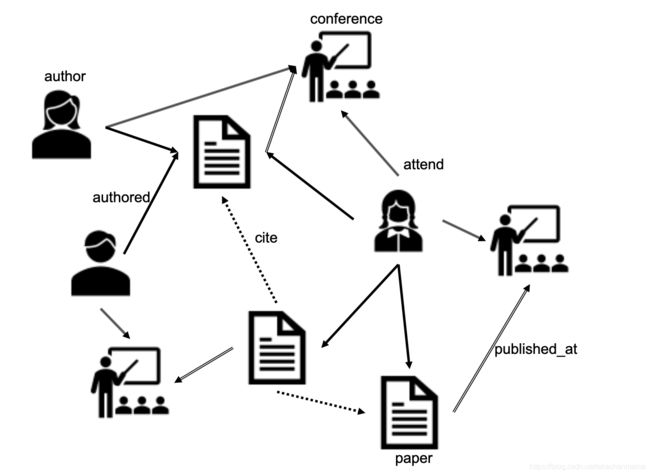
- 请通过继承
Data类实现一个类,专门用于表示“机构-作者-论文”的网络。该网络包含“机构“、”作者“和”论文”三类节点,以及“作者-机构“和“作者-论文“两类边。对要实现的类的要求:1)用不同的属性存储不同节点的属性;2)用不同的属性存储不同的边(边没有属性);3)逐一实现获取不同节点数量的方法。 - 根据Datawhale老师的提示,首先要在继承Data类的基础上定义新类的结构,然后定义属性方法,代码如下:
class MyData(Data):
def \_\_init\_\_(self, institution\_x, author\_x, paper\_x, work\_edge\_index, publish\_edge\_index, work\_edge\_attr, publish\_edge\_attr, y, \*\*kwargs):
super().\_\_init\_\_(\*\*kwargs)
self.institution\_x \= institution\_x
self.author\_x \= author\_x
self.paper\_x \= paper\_x
self.work\_edge\_index \= work\_edge\_index
self.publish\_edge\_index \= publish\_edge\_index
self.work\_edge\_attr \= work\_edge\_attr
self.publish\_edge\_attr \= publish\_edge\_attr
self.y \= y
@property
def num\_nodes\_institution(self):
return self.institution\_x.shape\[0\]
@property
def num\_nodes\_author(self):
return self.author\_x.shape\[0\]
@property
def num\_nodes\_paper(self):
return self.paper\_x.shape\[0\]
参考资料
- Datawhale GNN 组队学习资料
- Zhihu-茴郁蓁
- torch_geometric.data.Data
- torch_geometric.datasets.Planetoid