python金融分析小知识(25)——如何计算股票每日的收益率并进一步计算净值
Hello 大家好,我是一名新来的金融领域打工人,日常分享一些python知识,都是自己在学习生活中遇到的一些问题,分享给大家,希望对大家有一定的帮助!
相信有很多小伙伴在平时的金融数据分析中肯定有遇到需要计算股票每日的收益率的情况,那么如何通过python来计算股票的收益率呢?
就比如你今天有20元钱的股票,明天股票变成了30元钱,那么你的收益率就是(30-20)/ 20 = 0.5,这就是简单收益率的计算方法。
下面我们通过实际的股票收盘价以及python代码来实现股票每日收益率的计算:
1.简单收益率的计算
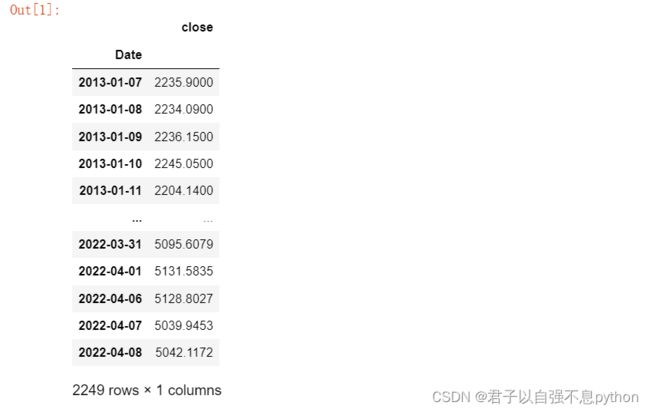
还是先读入股票收盘价数据:
import pandas as pd
data = pd.read_excel('万得全A收盘价.xlsx',index_col=[0],parse_dates=[0])
data下面计算股票每日收益率,我们通过pct_change方法就可以实现股票每日收益率的计算,pct_chage函数的作用是用于:表示当前数据与先前数据的相差百分比,其中可以指定periods=n,表示当前数据与先前n个数据的相差百分比。
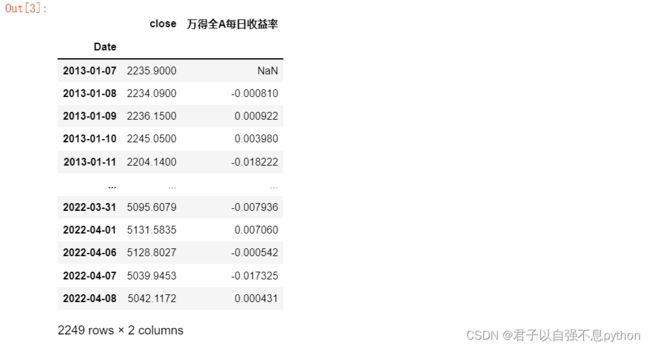
data['万得全A每日收益率'] = data['close'].pct_change(1)我们看看结果,相当于给我们新增了一列用于存放收益率:
2.对数收益率的计算
其实在金融分析中计算股票每日收益率的方法除了简单收益率外还有一种方法:对数收益率。两者是有一定的区别的,简单收益率是用于描述相邻两个价格的变化率,而对数收益率是指所有价格取对数之后,两两之间的差值。
就比如你今天有20元钱的股票,明天股票变成了30元钱,那么你的简单收益率就是(30-20)/ 20 = 0.5,你的对数收益率就是ln(30)-ln(20) = in(30/20) = 0.41。
那么为什么会存在对数收益率这种表达形式呢?因为对数收益率是具有可加性的。如果你计算了5天的对数收益率,你想得到第5天相对于第1天的绝对收益率,那么你可以直接把这五天的对数收益率进行累加就可以得到,其累加之和就是股票在期末的净值,也就是第5天收盘价相对于第1天收盘价的倍数。
具体代码如下:
data['万得全A每日对数收益率'] = np.log(data['close'] / data['close'].shift(1)) #np.log什么都不写代表自然对数
## 或者
data['万得全A每日对数收益率1'] = np.log(data['close']).diff(1)看看结果,后两列数据是完全相同的:
3.进一步讨论对数收益率的可加性用于计算净值
在我的前面的文章中有介绍股票净值的计算:python金融分析小知识(21)——如何计算股票、基金的收益净值曲线并通过python绘制 那么我们其实也可以利用对数收益率的可加性来计算净值,代码如下:
# 将对数收益率列进行求和(累加)
data[['万得全A每日对数收益率']].sum().apply(np.exp)结果如下,我们可以看出累加后的对数收益率为2.255073:
万得全A每日对数收益率 2.255073
dtype: float64那么这个时候我们股票的净值是多少呢?我们直接用期末的收盘价 / 期初的收盘价:
我们发现这两个结果其实是一样的, 也就是说我们可以直接对数收益率进行累加,其累加之和就是股票在期末的净值,也就是期末的收盘价相对于期初的收盘价的倍数。
接下来我们试着通过计算对数收益率,来得到股票的每日净值,乘以1代表净值从1开始:
data['万得全A累计收益——对数'] = 1*data[['万得全A每日对数收益率']].cumsum().apply(np.exp)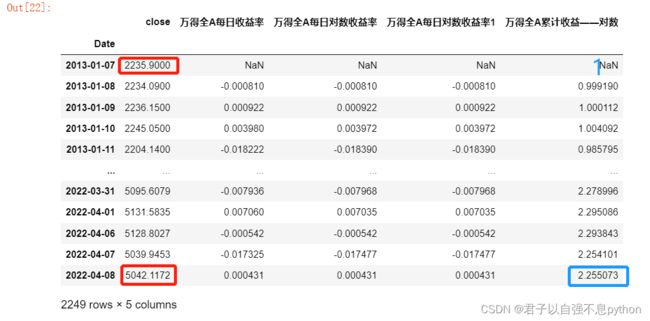 这也就意味着,如果我们从2013-01-07起手中一直持有“万得全A”这支股票,那么直到2022-04-08这一天,我们在一开始手里的1元钱就会变成如今的2.255元钱!
这也就意味着,如果我们从2013-01-07起手中一直持有“万得全A”这支股票,那么直到2022-04-08这一天,我们在一开始手里的1元钱就会变成如今的2.255元钱!
4.进一步讨论简单收益率用于计算净值
简单收益率计算净值其实是一个累乘的过程,也就是 P0(1+R)^t = Pt,其中R为每日收益率,t代表有多少日,代码里面乘以1代表净值从1开始:
data['万得全A累计收益'] = 1*(data['万得全A每日收益率']+1).cumprod(axis = 0)我们看看结果,结果包括股票的每日净值,可以发现采用简单收益率计算净值其最后得到的结果也是2.255073,和上面采用对数收益率计算结果一样:
总结:通过对数收益率和简单收益率我们都可以进行股票净值的计算,两种方法计算结果一样,这也就意味着,如果我们从2013-01-07起手中一直持有“万得全A”这支股票,那么直到2022-04-08这一天,我们在一开始手里的1元钱就会变成如今的2.255元钱!
最后我们汇总一下结果:
好啦,今天的文章就分享到这里啦!