Matlab：多输入多输出非线性对象的模型预测控制(MPC, Model Predictive Control)的实现

• Matlab MIMO MPC文档首页： Model Predictive Control of a Multi-Input Multi-Output Nonlinear Plant - MATLAB & Simulink - MathWorks 中国

✨ 本文展示了如何在Simulink中设计多输入多输出对象的闭环模型预测控制 (MPC, Model Predictive Control)，分析对象具有三个操纵变量(Manipulated Variables)与两个测量输出(Measured Output)。

一、非线性对象的线性化

1.1 线性化过程

在Matlab中使用open('mpc/mpcnonlinear')命令可以打开Simulink已经实现好的而非线性对象模型mpc_nonlinmodel，如下图所示：

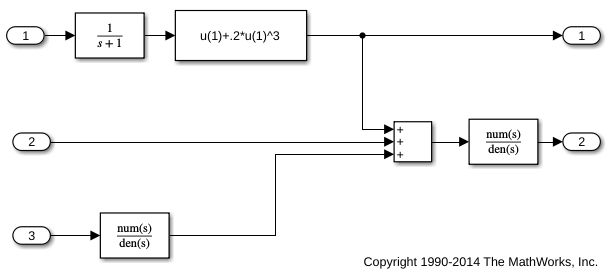
使用Simulink控制设计工具箱中的线性命令，在默认操作条件下（传递函数块的初始状态均为零）对对象进行线性化：

plant = linearize('mpc_nonlinmodel');

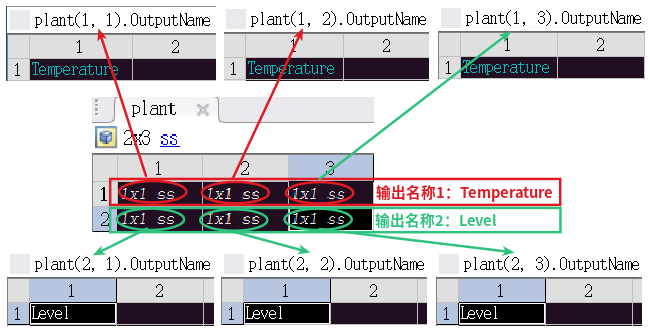
✨ linearize函数的作用是对Simulink模型或子系统进行线性近似。plant对象是一个$2\times 3$的状态空间模型(ss, State Space Model)矩阵，其中plant矩阵中的每个元素的数据结构为ss。以其中的plant(1, 1)为例，查看ss的数据结构。

• plant的数据结构如下图所示：

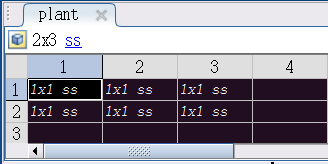
• plant(1, 1)的数据结构详细信息如下图所示：

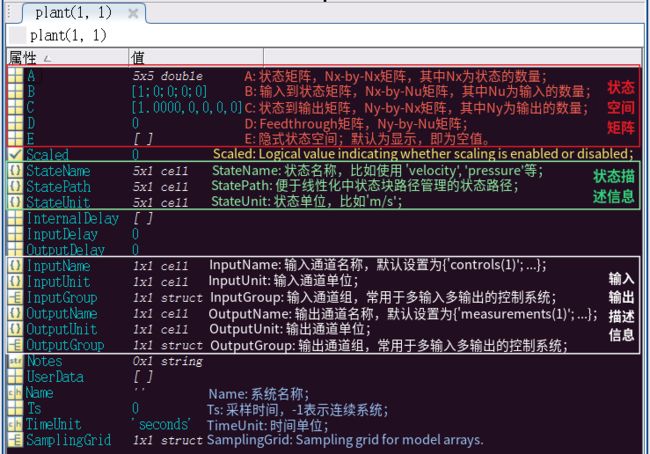
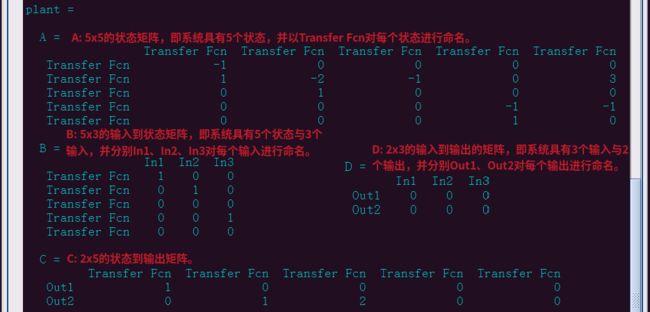
执行完plant = linearize('mpc_nonlinmodel');后，在命令窗口输入plant可以查看其主要参数信息如下图所示，结合上面的介绍，我们可以很容易地理解每个参数的含义：

1.2 I/O变量分配名称

• 1、为输入名称变量分配名称：

代码如下所示：

plant.InputName = {'Mass Flow';'Heat Flow';'Pressure'};

代码执行结果如下图所示：

• 2、为输出名称变量分配名称：

代码如下所示：

plant.OutputName = {'Temperature'; 'Level'};

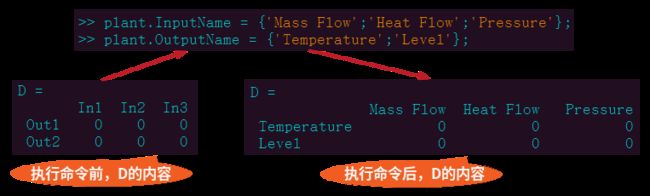
代码执行结果如下图所示：

经过为输入输出变量分配名称操作后，plant中输入输出变量名称则变为如下图所示的结果：

• 3、为输入单位变量分配名称：

代码如下所示：

plant.InputUnit = {'kg/s', 'J/s', 'Pa'};

• 4、为输出单位变量分配名称：

plant.OutputUnit = {'K', 'm'};

经过为输入输出单位变量分配名称后，plant中输入输出单位变量的结果如下图所示：

二、设计模型预测控制(MPC, Model Predictive Control)控制器

• 1、构造MPC控制器对象

下面的指令构造MPC控制器，其中设置参数如下所示：

• (1) 采样率(sampling period)：0.2 sec；
• (2) Prediction horizon：5 steps；
• (3) Prediction horizon：2 moves；

mpcobj = mpc(plant, 0.2, 5, 2);

通过get命令可以获得mpcobj的类属性，每个类属性的内涵如下图所示：

• 2、设置操纵变量的约束与权重

设置模型预测控制对象mpcobj操纵变量的指令如下所示：

mpcobj.MV = struct('Min',{-3;-2;-2},'Max',{3;2;2},'RateMin',{-1000;-1000;-1000});

设置模型预测控制对象mpcobj权重的指令如下所示：

mpcobj.Weights = struct('MV', [0 0 0], 'MVRate', [.1 .1 .1], 'OV', [1 1]);

执行完指令后，通过mpcobj命令可以查看其属性。

三、使用Simulink进行闭环仿真

通过下面的指令可以打开Matlab中的Simulink闭环仿真模型mpc_nonlinear：

mdl1 = 'mpc_nonlinear';
open_system(mdl1)

打开的mpc_nonlinear模型包括如下图所示的三个部分：

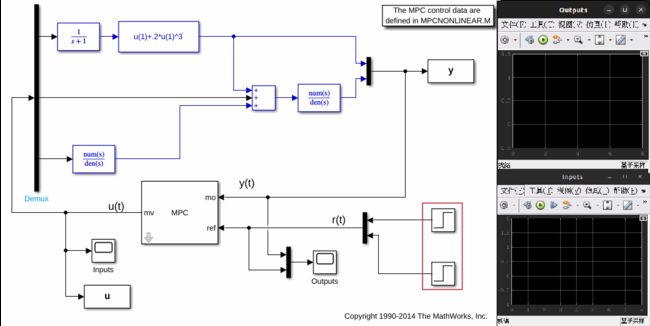
通过下面的命令就可以进行仿真了：

sim(mdl1)

运行结果如下图所示：

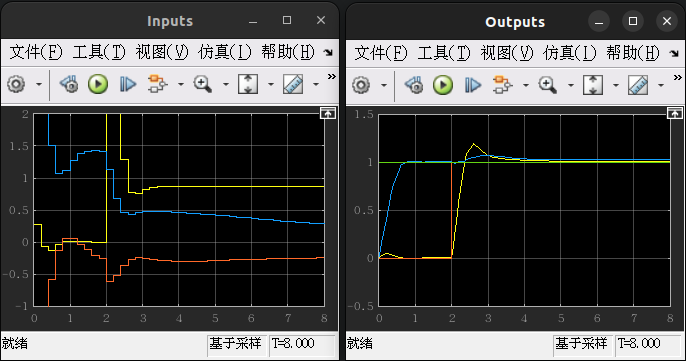
由上图分析结果可以看出，尽管存在非线性，但是两个输出在几秒后很好地跟踪其参考值，并且操纵变量仍然保持在设置的约束内。

四、修改MPC设计跟踪斜坡信号

为了在补偿非线性的同时跟踪斜坡，将两个输出上的扰动模型定义为三积分器（没有非线性，双积分器就足够了）。

通过tf函数构造一个外部扰动模型outdistmodel：

outdistmodel = tf({1 0; 0 1}, {[1 0 0 0], 1; 1, [1 0 0 0]});

构造的传递函数矩阵为：

$$\left[\begin{array}{cc}\frac{1}{s^3}& 0\\ 0& \frac{1}{s^3}\end{array}\right]$$

通过setoutdist函数将上面构造的不可观测外部扰动传递函数outdistmodel添加到MPC的model中：

setoutdist(mpcobj, 'model', outdistmodel);

打开Simulink中的闭环仿真模型mpc_nonlinear_setoutdist，它与上面的mpc_nonlinear闭环Simulink仿真模型相同，唯一不同的是参考信号，其参考信号的第一个由阶跃变为3秒以内以0.2斜率上升的斜坡信号。

打开的mpc_nonlinear_setoutdist模型包括如下图所示的三个部分：

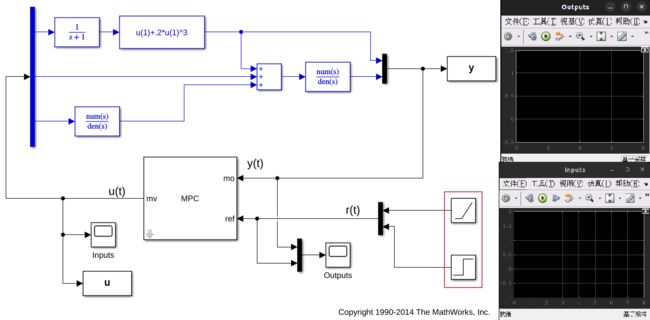
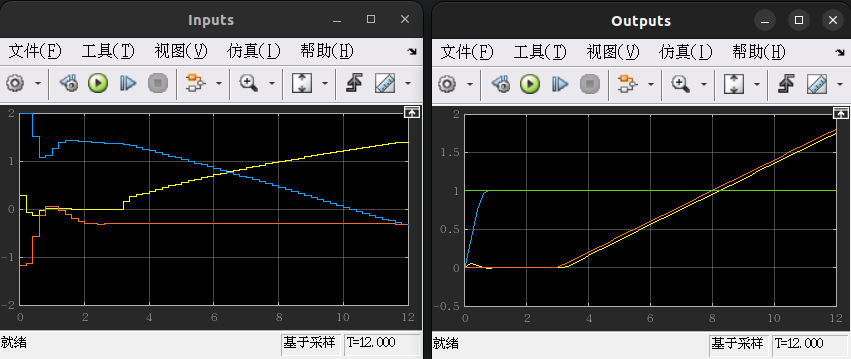
下面的执行将mpc_nonlinear_setoutdist模型仿真12s：

sim(mdl2, 12)

仿真结果如下图所示：