LSTM语音识别
文章目录
- 前言
- 一、绪论
-
- 1.1 语音识别的意义
- 1.2 语音识别的现状
- 1.3 课题研究方向
- 二、语音识别基本原理
-
- 2.1 发声机理
- 2.2 识别原理
- 2.3 频域分析
- 2.3.1 离散傅里叶变换
- 2.3.3 Mel频率
- 2.3.4 同态解卷积
- 2.4 Mel频率倒谱系数
- 三、声学模型
-
- 3.1 隐马尔可夫模型
- 3.1.1 模型参数
- 3.1.2 假设
- 3.1.3 HMM解码
- 3.2 深度神经网络
- 3.2.1 DNN的意义
- 3.2.3 反向传播
- 3.3 循环神经网络
- 3.3.1 RNN
- 3.3.2 LSTM
- 3.3.3 BLSTM
- 四、CTC
-
- 4.1 CTC解码
- 4.2转录损耗
前言
机器学习大多数属于浅层模型(GMM、HMM等),浅层模型非线性变换能力较弱,不足以刻画复杂的语音数据(高维特征),识别性能提升非常有限,因此本课题针对声学模型GMM-HMM进行改进。由于GMM的输入是单帧,忽视了协同发音的影响,采用拼接帧作为深度神经网络(DNN)的输入对观测概率建模。传统的HMM和RNN都可以对时序建模,由于HMM是浅层模型以及RNN存在梯度消失问题,采用双向长短期记忆网络(BLSTM)对时序建模。端到端问题需要强制对齐后才能进行训练,人工对齐所需的时间开销巨大,采用基于联结主义时序分类器(CTC)的方法解决。实验结果表明,基于DNN-LSTM端到端语音识别在thchs30上的错词率为4%。最后将此识别系统为核心实现自动添加字幕,减小制作视频周期。
一、绪论
1.1 语音识别的意义
人类能够走向文明社会,在于人类在生存竞争中学到许多经验,并且不断的流传积累。而经验流传的最有效的方式就是语言交流,所以语言对于人类的发展很重要。由于语言的多样性,对于不同地区的人们之间的交流形成一定的阻碍。随着技术发展诞生了机器翻译,机器翻译冲破这些的障碍成为可能,而实现语音到语音的机器翻译的前提就是语音识别。
今年初,由于新冠肺炎疫情的影响,对人们的出行造成了很大的阻碍。例如在电梯里,病毒可能附着在触控面板上,在按电梯按钮的时候会增加直接接触病毒的风险,语音识别为实现无接触式操控提供了可能,从而降低感染的风险。在正常日常生活中,智能语音音箱,手机语音助手,公共场合的引导系统等,都离不开语音识别,其他有价值的应用还有待挖掘。所以本文将围绕语音识别的具体实现以及应用展开分析。
1.2 语音识别的现状
20世纪50年代,贝尔实验室成功开发出一款能够识别10个数字的孤立词识别系统 [ 1 ] ^{[1]} [1],从此拉开了语音识别系统研究的帷幕。在此后的几十年时间里进展缓慢,由于隐马尔可夫模型(HMM)可以对时间序列建模 [ 2 , 3 ] ^{[2,3]} [2,3],因此在20世纪80年代开始HMM在语音识别的中成为重点研究对象,例如李开复在读期间开发的基于GMM-HMM的SPHINX系统 [ 4 ] ^{[4]} [4]。HMM有两个重要的参数,即转移概率和观测概率,GMM(高斯混合模型)就是对后者进行估计(建模)。20世纪80年代后期,人们尝试将人工神经网络引入语音识别,但是由于当时算力的不足以及网络结构复杂,导致其效果不如基于GMM-HMM的识别系统 [ 5 , 6 ] ^{[5,6]} [5,6]。
2006年,Hinton对神经网络节点使用受限波尔兹曼机(RBM)进行初始化 [ 7 ] ^{[7]} [7],解决了深度神经网络训练过程容易陷入局部最优的问题,三年后,Hinton和Mohame D [ 8 ] ^{[8]} [8] 成功将深度置信网络(DBN)在小词汇量TIMIT上实现连续语音识别。2011-2012年,俞栋、邓力和Hinton等人将DNN(深度神经网络)替换声学模型GMM-HMM中的GMM对观测概率的估计,将DNN-HMM应用在大词汇量连续语音识别上,词错率降低了30% [ 9 ] ^{[9]} [9],取得了较大的进步。2015年10月,清华大学王东使用DNN-HMM在清华开源中文语音数据集thchs30上实现大词汇量连续中文语音识别,词错率达到23.3% [ 10 ] ^{[10]} [10]。
由于DNN-HMM需要分别训练两个模型,并且不能解决长期依赖问题。循环神经网络(RNN)具有一定的“记忆”功能,在对时间序列问题的处理优于DNN-HMM框架。因此RNN在语音识别中得到广泛的应用。但是RNN存在一些问题,就是在反向传播过程中,隐藏层间的矩阵偏导数包含指数部分,会导致梯度消失或梯度爆炸 [ 11 ] ^{[11]} [11],因此不能解决更长的依赖问题。为此HOCHREITER S [ 12 ] ^{[12]} [12]等人为了克服梯度消失或者梯度爆炸,提出在RNN的基础上增加“门”结构控制信息流,即长短期记忆网络(LSTM)。双向结构LSTM比单向LSTM在长期依赖问题上处理得更好。但是双向LSTM需要读取完整段语音特征数据才能处理,因此实时性差。
双向LSTM不仅实时性差,而且网络结构复杂,需耗费大量的计算资源,对此讯飞(2015年)提出了前馈序列记忆网络(FSMN),FSMN在DNN的隐藏层加入记忆单元,实现非循环的前馈结构,最终将词错率降至13.2% [ 13 ] ^{[13]} [13]。
1.3 课题研究方向
本课题将围绕建模能力、上下文相关以及强制对齐这三个问题展开讨论。在声学模型GMM-HMM的基础上进行改进,使用DNN对观测概率的估计,将建模能较力弱的浅层HMM用RNN替换。由于RNN存在梯度消失问题,导致上下文相关性不强,基于RNN改进的LSTM,LSTM通过增加“门”结构,一些重要的信息得到保留。为了使上下文相关性更强,使用双向结构的LSTM,双向LSTM不仅学习历史信息,还学习未来的信息。
本课题的目标就是打造一个黑盒,即喂入音频吐出对应文本,不需要手动强制对齐音频和标签。联结主义时序分类器(Connectionist Temporal Classification,CTC)不需要强制对齐,连续且相同的字符,只输出最大概率的字符,并引入一个空状态替换重复的字符,因此CTC不需要一一对齐,输出是一串尖峰序列。直接将CTC的转录损耗期望作为损失函数,就可以进行训练了。因为转录损耗期望的后验概率维度太复杂,采用MCMC采用作为输入。
4G时代将视频服务逐渐趋于移动端,视频邻域快速增长,尤其是短视频和Vlog。而然视频的制作很耗时,特别是添加字幕,带字幕的视频能增加用户体验,所以本课题从这一朴素的想法出发。首先从视频中提取音频,然后将音频作为语音识别系统的的输入,系统输出对应文本,最后将文本添加到视频中作为字幕。
二、语音识别基本原理
2.1 发声机理
当人在说话时,胸腔作为动力源产生气流,气流经过气管,当声门打开时,声带不振动或振动频率很小,发出的音为辅音,其波形类似于白噪声;由于声门有一定的韧性,所以当声门闭合时,声带在气流的冲击下,声门不断的开启和闭合,产生高频振动,这就是所谓的元音。在语音信号的线性产生模型中,声带作为激励源,声道作为共振腔。当声道的形状不同时,声道能谐振出不同的频率,不同的频率对应着不同的元音。由于每个人的声带都不相同,声带的振动频率不同,所以这是能区别不同人的重要特征,这些特征可用基因周期来描述。
2.2 识别原理
语音识别系统分成前端处理和后端处理,前端为信号处理,包括端点检测和声学特征提取等,端点检测可用短时能量和短时过零率描述,使用Mel频率倒谱系数作为声学特征。后端处理有语言模型、声学模型和解码搜索。声学特征矢量经过训练得到声学模型,语言模型词的链式概率得到。结合语言模型和声学模型,利用最大后验概率(MAP)得到词向量,其公式为
W ~ = arg max w P ( W ∣ O 1 ⊤ ) = arg max w P ( O 1 ⊤ ∣ W ) P ( W ) P ( O 1 ⊤ ) ∝ arg max w P ( O 1 ⊤ ∣ W ) P ( W ) (2-1) \begin{aligned}\tilde{W} &=\arg \max _{w} P\left(W \mid O_{1}^{\top}\right) \\ &=\arg \max _{w} \frac{P\left(O_{1}^{\top} \mid W\right) P(W)}{P\left(O_{1}^{\top}\right)} \\ & \propto \arg \max _{w} P\left(O_{1}^{\top} \mid W\right) P(W)\end{aligned}\tag{2-1} W~=argwmaxP(W∣O1⊤)=argwmaxP(O1⊤)P(O1⊤∣W)P(W)∝argwmaxP(O1⊤∣W)P(W)(2-1)
式中, P ( W ) P(W) P(W)为语言模型, P ( W ∣ O 1 ⊤ ) P\left(W \mid O_{1}^{\top}\right) P(W∣O1⊤)为声学模型, P ( O 1 ⊤ ) P(O_{1}^{\top}) P(O1⊤)为声学特征的概率,和词向量无关,所以可以去掉。
2.3 频域分析
2.3.1 离散傅里叶变换
傅里叶变换分为连续傅里叶变换和离散傅里叶变换DFT [ 14 ] ^{[14]} [14],因为语音信号经采样后存储在计算机内的是离散信号,所以我们要用到的是DFT。将语音分帧后,要在每一帧提取一组13个MFCC系数作为语音的特征。每一帧经过一个DFT得到一个频谱,数学表达式如(2-2)所示。
X i ( k ) = ∑ n = 1 N x i ( n ) w ( n ) e − j 2 π k n N , 0 ≤ k ≤ N (2-2) X_{i}(k)=\sum_{n=1}^{N} x_{i}(n) w(n) e^{-j \frac{2 \pi k n}{N}}, 0 \leq k \leq N\tag{2-2} Xi(k)=n=1∑Nxi(n)w(n)e−jN2πkn,0≤k≤N(2-2)
x i ( n ) x_{i}(n) xi(n)表示第i帧语音信号,w(n)是窗长为N个采样点的窗函数(例如汉明窗),并且K是离散傅里叶的长度。
2.3.2能量谱
在时域上很难观察出语音信号的一些重要特性,需要将语音信号通过DFT变换到频域上,在频域取平方得到能量分布,然后研究共振峰以及变换过程,即谱包络,对基音周期还可以研究频谱,不同的能量谱,对应着不同的特性能量谱的数学表达式为(2-3)。
E i ( k ) = ∣ X i ( k ) ∣ 2 (2-3) E_i(k)=\left | X_i(k) \right | ^2\tag{2-3} Ei(k)=∣Xi(k)∣2(2-3)
2.3.3 Mel频率
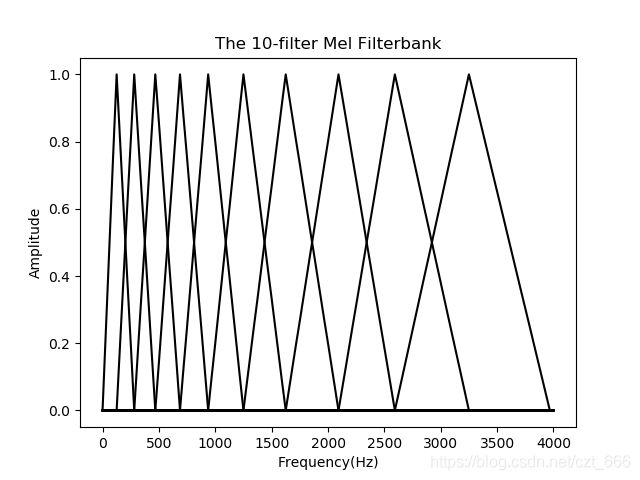
人的耳蜗能共振不同的频率,频率的变化是非线性的。研究人员设计出一组类似于人耳蜗的滤波器组,滤波器为三角滤波器,中心频率是按照Mel频率刻度均匀排列,图2.3.1为10个三角滤波器组成的Mel滤波器组[5],滤波器组的数学表达式为(2-4)。
H m ( k ) = { k − f ( m − 1 ) f ( m ) − f ( m − 1 ) , f ( m − 1 ) < k ≤ f ( m ) f ( m + 1 ) − k f ( m + 1 ) − f ( m ) , f ( m ) < k ≤ f ( m + 1 ) 0 , 其 他 (2-4) H_m(k)=\begin{cases} \frac{k-f(m-1)}{f(m)-f(m-1)},f(m-1)
式(2-4)中,M表示滤波器的个数, f ( m ) f(m) f(m)为中心频率。 f ( m ) f(m) f(m)的定义如下:
f ( m ) = ( N f s ) M − 1 [ M ( f 1 ) + m M ( f h ) − M ( f 1 ) M + 1 ] (2-5) f(m)=\left(\frac{N}{f_{s}}\right) M^{-1}\left[M\left(f_{1}\right)+m \frac{M\left(f_{h}\right)-M\left(f_{1}\right)}{M+1}\right]\tag{2-5} f(m)=(fsN)M−1[M(f1)+mM+1M(fh)−M(f1)](2-5)
式(2-5)中,为采样频率,为FFT的长度,为滤波器的最小频率,为滤波器的最小频率。 M ( f ) M(f) M(f)表示将线性频谱转换为Mel非线性频谱,其换算公式为:
M ( f ) = 1125 log ( 1 + f 700 ) (2-6) M(f)=1125 \log \left(1+\frac{f}{700}\right)\tag{2-6} M(f)=1125log(1+700f)(2-6)
2.3.4 同态解卷积
声门的作为激励源,当频率等于声道(口腔)的固有频率时,声道会产生谐振,此时谐振的频率被称为共振峰。口腔肌肉属于软组织,能吸收声带振动时产生的能量,因此可以将口腔看作是一个阻尼大的共振器。当口腔形状不同时,更一般的来说,当声道(口腔、舌位和唇)不同时,能共振不同的频率,不同的频率也对应着不同的元音,所以共振峰是描述声道特性的重要参数,共振峰频率与舌位的关系如图所示。
语音信号等于声门激励信号与声道响应信号的卷积。所以为了对共振峰进行估计,可以对解卷积,得到和,即对应着能量谱上的谱包络。将和波形的变化快慢抽象理解为高频和低频,然后映射到伪频率坐标上,这就是所谓的倒谱,公式如(2-7)所示。因此在倒谱用低通滤波器和高通滤波器就可以得到共振峰(低频部分)和基音周期(高频部分)。
C E P i ( k ) = DFT − 1 ( ln ∣ E i ( k ) ∣ ) (2-7) C E P_{i}(k)=\text { DFT }^{-1}\left(\ln \left|E_{i}(k)\right|\right)\tag{2-7} CEPi(k)= DFT −1(ln∣Ei(k)∣)(2-7)
式(2-7), D F T − 1 DFT^{-1} DFT−1为 D F T DFT DFT的逆变换。
2.4 Mel频率倒谱系数
Mel频率倒谱系数(Mel Frequency Cepstrum coefficient,MFCC)就是在Mel频谱上进行倒谱分析。简单来说就是帧信号经过DFT后,得到的结果平方,即得到功率谱,然后经过Mel频率滤波器组将线性频率映射到非线性Mel频率上,其对结果进行同态解卷积。计算过程如下:语音信号经过DFT得到频谱;然后平方得到能量谱,通入Mel频率滤波器组转换到Mel频率上,每个滤波都有叠加部分;将每个滤波器的输出进行同态解卷积,即进行对数处理,得到相应的对数功率谱log,然后进行反离散余弦变换(Discrete Cosine Transform,DCT),一般取DCT后的12~16个系数作为MFCC系数,公式为(2-8)。
C n = ∑ k = 1 M log x ( k ) cos [ π ( k − 0.5 ) n / M ] , n = 1 , 2 , ⋯ , L (2-8) C_{n}=\sum_{k=1}^{M} \log x(k) \cos [\pi(k-0.5) n / M], n=1,2,\cdots,L\tag{2-8} Cn=k=1∑Mlogx(k)cos[π(k−0.5)n/M],n=1,2,⋯,L(2-8)
MFCC特征只描述了一个信号帧的能量谱包络,只能将其作为静态特征。做一阶和二阶差分得到对应的delta系数(动态特征),其公式为(2-9)。特征矢量等于静态特征加上动态特征,静态特征取13个时,特征矢量的长度为26。
d t = ∑ n = 1 N n ( c t + n − c t − n ) 2 ∑ n = 1 N n 2 (2-9) d_{t}=\frac{\sum_{n=1}^{N} n\left(c_{t+n}-c_{t-n}\right)}{2 \sum_{n=1}^{N} n^{2}}\tag{2-9} dt=2∑n=1Nn2∑n=1Nn(ct+n−ct−n)(2-9)
三、声学模型
3.1 隐马尔可夫模型
3.1.1 模型参数
HMM的模型参数 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B), π \pi π表示初始状态概率矢量 [ a i j ] N × N [a_{ij}]_{N\times N} [aij]N×N,A表示状态转移矩阵,B表示观察概率矩阵 [ b j k ] N × M [b_{jk}]_{N\times M} [bjk]N×M。 a i j a_{ij} aij表示第i个状态转移到第j个状态的概率, b j k b_{jk} bjk表示第j个状态的第k个发射概率。
3.1.2 假设
①齐次马尔可夫假设:t时刻的状态只和t-1时刻有关,用条件概率表示为:
p ( i t + 1 ∣ i t , i t − 1 , ⋯ , i 1 , o t , o t − 1 , ⋯ , o 1 ) = p ( i t + 1 ∣ i t ) (3-1) p\left(i_{t+1} \mid i_{t}, i_{t-1}, \cdots, i_{1}, o_{t}, o_{t-1}, \cdots, o_{1}\right)=p\left(i_{t+1} \mid i_{t}\right)\tag{3-1} p(it+1∣it,it−1,⋯,i1,ot,ot−1,⋯,o1)=p(it+1∣it)(3-1)
② 观测独立性假设:任意一时刻的观测只和当前时刻有关,用条件概率表示为:
p ( o t ∣ i t , i t − 1 , ⋯ , i 1 , o t − 1 , ⋯ , o 1 ) = p ( o t ∣ i t ) (3-2) p\left(o_{t} \mid i_{t}, i_{t-1}, \cdots, i_{1}, o_{t-1}, \cdots, o_{1}\right)=p\left(o_{t} \mid i_{t}\right)\tag{3-2} p(ot∣it,it−1,⋯,i1,ot−1,⋯,o1)=p(ot∣it)(3-2)
3.1.3 HMM解码
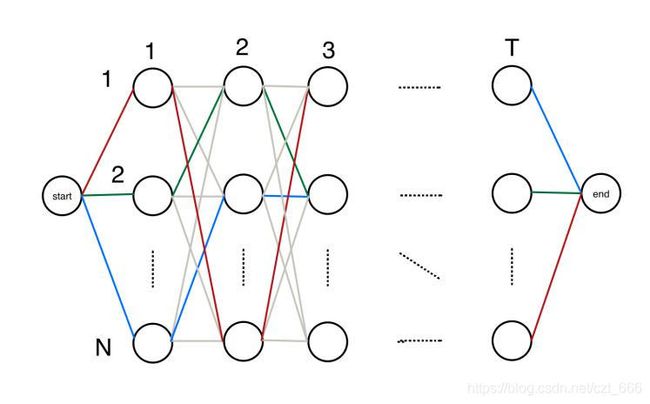
由(2-1)式可知,给定语音信号的条件下,求最大概率的词序列 o = ( o 1 , o 2 , ⋯ , o T ) o=(o_1,o_2,\cdots,o_T) o=(o1,o2,⋯,oT),将语音信号看作HMM的观测序列,词序列看作HMM的隐状态序列 s = ( s 1 , s 2 , ⋯ , s T ) s=(s_1,s_2,\cdots,s_T) s=(s1,s2,⋯,sT),因此语音识别对应于HMM的解码问题。因为任意的状态都对应着一个观测概率分布 q = ( q 1 , q 2 , ⋯ , q N ) q=(q_1,q_2,\cdots,q_N) q=(q1,q2,⋯,qN),因此解码问题的计算复杂度为 N T N^T NT。基于动态规划的算法,Viterbi算法将语音识别的最大概率p等价于最短路径 1 p \frac{1}{p} p1,计算并记录t时刻所有节点的最短路径,这是一个前向过程,直到T时刻结束,如图3.1.2,选择红绿蓝中最短的路径作为结果。
3.2 深度神经网络
3.2.1 DNN的意义
在算力的不断提高以及数据不断的增长的背景之下,深度学习迎来高速发展。相对于传统的浅层模型,深层模型对复杂的数据建模能力更强,归功于模型中具有多层的非线性变换(能区分更多的类别)的隐层,所以深度学习在学术界和工业界得到了高度重视。图3.2.1 DNN网络结构图
深度神经网络(Deep Neural Network,DNN) [ 15 ] ^{[15]} [15]可以有多层隐层,每层隐层的节点数很多,虽然每个节点只有简单的非线性变换,但是多个隐层组合起来就能产生出非常复杂的非线性变换,所以DNN能将原始输入特征转换为更加具有不变性和鉴别性的特征,这些特征便于用分类器分类。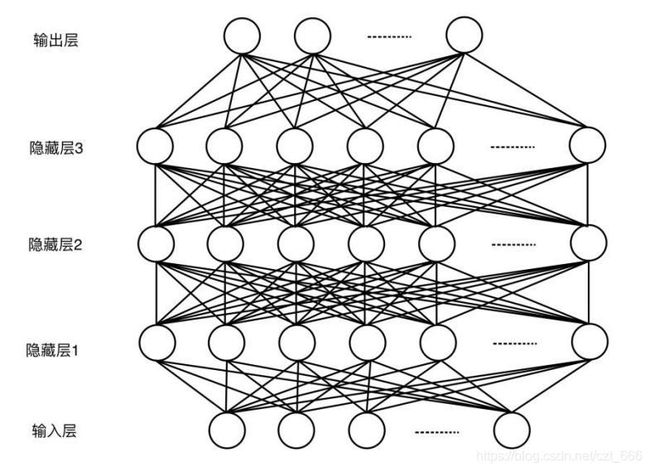 3.2.2前向传播
3.2.2前向传播
DNN由许多神经元构成,神经元就是所谓的感知机,其结构为图3.2.2所示。感知机是将输入线性加权的线性分类模型经过激活函数后变成非线性分类模型,非线性分类模型具有更优的决策边界,感知机的数学表达式为(3-3),式中 v 0 v^0 v0表示输入层。计算完隐藏层1所有的神经元后,用同样的方式计算下一层。对于分类任务,输出层每个神经元表示一个类别,输出的是每一个类别 i ∈ { 1 , 2 , ⋯ , C } i \in \left \{ 1,2,\cdots,C \right \} i∈{1,2,⋯,C}的概率值,输出层 v L v^L vL满足 v L ≥ 0 v^L\ge 0 vL≥0并且 ∑ i = 1 C v i L = 1 \sum_{i=1}^Cv_i^L=1 ∑i=1CviL=1,所以利用softmax(也是激活函数)进行归一化,softmax表达式为(3-4)。
v ℓ = f ( z ℓ ) = f ( W ℓ v ℓ − 1 + b ℓ ) , 0 < ℓ < L (3-3) v^{\ell}=f\left(z^{\ell}\right)=f\left(W^{\ell} v^{\ell-1}+b^{\ell}\right), 0<\ell<\mathrm{L}\tag{3-3} vℓ=f(zℓ)=f(Wℓvℓ−1+bℓ),0<ℓ<L(3-3)
v i L = soft max ( z i L ) = e z i L ∑ j = 1 c e z j L (3-4) v_{i}^{L}=\operatorname{soft} \max \left(z_{i}^{L}\right)=\frac{e^{z_{i}^{L}}}{\sum_{j=1}^{c} e^{z_{j}^{L}}}\tag{3-4} viL=softmax(ziL)=∑j=1cezjLeziL(3-4)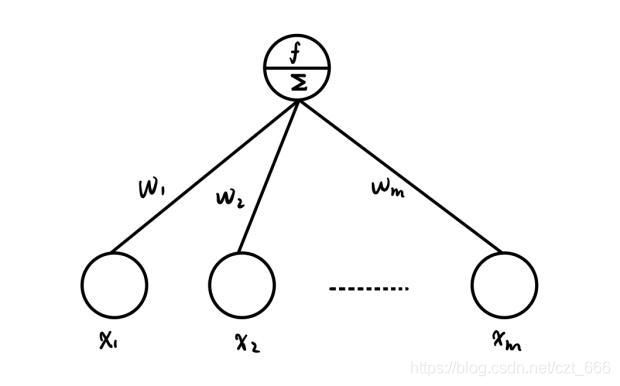
式(3-1)中, v ℓ v^{\ell} vℓ表示第 ℓ \ell ℓ层神经元向量的输出, w ℓ w^{\ell} wℓ为 ℓ \ell ℓ层和 ℓ − 1 \ell-1 ℓ−1层的权重矩阵, b ℓ b^\ell bℓ为 ℓ \ell ℓ层的偏置,激活函数 f ( ⋅ ) f(\cdot) f(⋅)有sigmoid函数、tanh函数和relu函数等,如图3.2.3所示。他们的表达式为(3-5)至(3-7)。 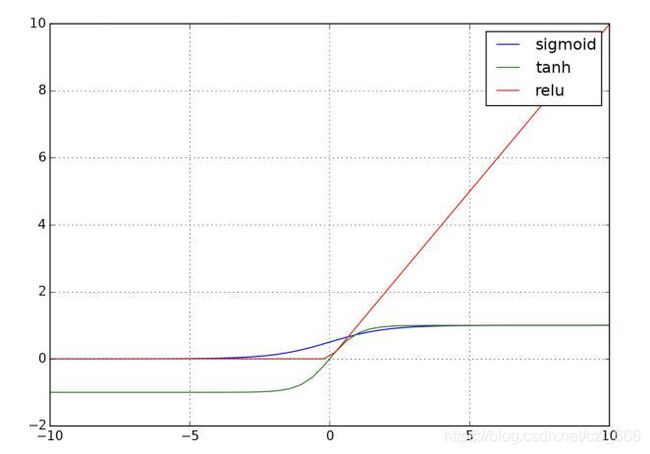 sigmoid ( x ) = 1 1 + e − x (3-5) \text { sigmoid }(x)=\frac{1}{1+e^{-x}}\tag{3-5} sigmoid (x)=1+e−x1(3-5)
sigmoid ( x ) = 1 1 + e − x (3-5) \text { sigmoid }(x)=\frac{1}{1+e^{-x}}\tag{3-5} sigmoid (x)=1+e−x1(3-5)
tanh ( x ) = e x − e − x e x + e − x (3-6) \tanh (x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\tag{3-6} tanh(x)=ex+e−xex−e−x(3-6)
relu ( x ) = max ( 0 , x ) (3-7) \operatorname{relu}(x)=\max (0, x)\tag{3-7} relu(x)=max(0,x)(3-7)
3.2.3 反向传播
DNN属于监督学习,目的是将输出值拟合真实值(观测),可以通过输出值与真实值之间的距离来度量。对分类任务的输出是概率分布,一般使用交叉熵(Cross Entropy,CE)来度量两个概率分布的相似度,可用(3-8)式表示。
J C E ( W , b ; o , y ) = − ∑ i = 1 c y i log v i L (3-8) J_{\mathrm{CE}}(W, \mathrm{b} ; o, \mathrm{y})=-\sum_{i=1}^{c} y_{i} \log v_{i}^{L}\tag{3-8} JCE(W,b;o,y)=−i=1∑cyilogviL(3-8)
式(3-8)中, o o o为观察序列, y y y是相应的输出序列, y i y_i yi是属于类别 i i i的经验分布(标注), v i L v_i^L viL是DNN估计的分布。我们的目的是拟合这两个分布,等价于最小化交叉熵损失函数,使用梯度下降学习参数(3-9)和(3-10),式中 ∇ b t ℓ \nabla b_{t}^{\ell} ∇btℓ ∇ W t ℓ \nabla W_{t}^{\ell} ∇Wtℓ分别为权重矩阵和偏置的偏导数,具体表达式为(3-11)和(3-12)。
W t + 1 ℓ ← W t ℓ − ε ∇ W t ℓ (3-9) W_{t+1}^{\ell} \leftarrow W_{t}^{\ell}-\varepsilon \nabla W_{t}^{\ell} \tag{3-9} Wt+1ℓ←Wtℓ−ε∇Wtℓ(3-9)
b t + 1 ℓ ← b t ℓ − ε ∇ b t ℓ (3-10) b_{t+1}^{\ell} \leftarrow b_{t}^{\ell}-\varepsilon \nabla b_{t}^{\ell} \tag{3-10} bt+1ℓ←btℓ−ε∇btℓ(3-10)
∇ t t ℓ J C E ( W , b ; o , y ) = ∇ z t ℓ J c E ( W , b ; o , y ) ∂ z t L ∂ W t L = e t L ∂ ( W t L v t L − 1 + b t L ) ∂ W t L = e t L ( v t L − 1 ) ⊤ = ( v t L − y ) ( v t L − 1 ) ⊤ (3-11) \nabla_{t_{t}^{\ell}} J_{C E}(W, b ; o, y)=\nabla_{z_{t}^{\ell}} J_{c E}(W, b ; o, y) \frac{\partial z_{t}^{L}}{\partial W_{t}^{L}} \\=e_{t}^{L} \frac{\partial\left(W_{t}^{L} v_{t}^{L-1}+b_{t}^{L}\right)}{\partial W_{t}^{L}} \\=e_{t}^{L}\left(v_{t}^{L-1}\right)^{\top} \\=\left(v_{t}^{L}-y\right)\left(v_{t}^{L-1}\right)^{\top}\tag{3-11} ∇ttℓJCE(W,b;o,y)=∇ztℓJcE(W,b;o,y)∂WtL∂ztL=etL∂WtL∂(WtLvtL−1+btL)=etL(vtL−1)⊤=(vtL−y)(vtL−1)⊤(3-11)
式(3-11)中, e t L = ∇ e t ι J C E ( W , b ; o , y ) = ∂ ∑ i = 1 c y i log soft max i ( z t L ) ∂ z t L = ∂ ∑ i = 1 c y i log ∑ j = 1 c e z j L ∂ z t L − ∂ ∑ i = 1 c y i log e z i L ∂ z t L = ∂ log ∑ j = 1 c e z j L ∂ z t L − ∂ ∑ j = 1 c y i z i L ∂ z t L = [ e z 1 L ∑ j = 1 c e z j L ⋮ e z i L ∑ j = 1 c e z j L ⋮ e z c L ∑ j = 1 c e z j L ] − [ y 1 ⋮ y i ⋮ y c ] = ( v t L − y ) \begin{aligned}e_{t}^{L} &=\nabla_{e_{t}^{\iota}} J_{C E}(W, b ; o, y) \\ &=\frac{\partial \sum_{i=1}^{c} y_{i} \log \operatorname{soft} \max _{i}\left(z_{t}^{L}\right)}{\partial z_{t}^{L}} \\&=\frac{\partial \sum_{i=1}^{c} y_{i} \log \sum_{j=1}^{c} e^{z_{j}^{L}}}{\partial z_{t}^{L}}-\frac{\partial \sum_{i=1}^{c} y_{i} \log e^{z_{i}^{L}}}{\partial z_{t}^{L}} \\ &=\frac{\partial \log \sum_{j=1}^{c} e^{z_{j}^{L}}}{\partial z_{t}^{L}}-\frac{\partial \sum_{j=1}^{c} y_{i} z_{i}^{L}}{\partial z_{t}^{L}}\\ &\begin{array}{l}=\left[\begin{array}{c}\frac{e^{z_{1}^{L}} }{\sum_{j=1}^{c} e^{z_{j}^{L}} }\\\vdots \\\frac{e^{z_{i}^{L}}}{\sum_{j=1}^{c} e^{z_{j}^{L}}} \\\vdots \\\frac{e^{z_{c}^{L}} }{\sum_{j=1}^{c} e^{z_{j}^{L}}}\end{array}\right]-\left[\begin{array}{l}y_{1} \\\vdots \\y_{i} \\\vdots \\y_{c}\end{array}\right] \\ &=\left(v_{t}^{L}-y\right)\end{array}\end{aligned} etL=∇etιJCE(W,b;o,y)=∂ztL∂∑i=1cyilogsoftmaxi(ztL)=∂ztL∂∑i=1cyilog∑j=1cezjL−∂ztL∂∑i=1cyilogeziL=∂ztL∂log∑j=1cezjL−∂ztL∂∑j=1cyiziL=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡∑j=1cezjLez1L⋮∑j=1cezjLeziL⋮∑j=1cezjLezcL⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤−⎣⎢⎢⎢⎢⎢⎢⎡y1⋮yi⋮yc⎦⎥⎥⎥⎥⎥⎥⎤=(vtL−y) ∇ b t ι J C E ( W , b ; o , y ) = ( v t L − y ) (3-12) \nabla_{b_{t}^{\iota}} J_{C E}(W, b ; o, y)=\left(v_{t}^{L}-y\right)\tag{3-12} ∇btιJCE(W,b;o,y)=(vtL−y)(3-12)
3.3 循环神经网络
3.3.1 RNN
使用MFCC来描述语音信号,即将MFCC作为语音信号的特征矢量,然后训练声学模型来寻找特征矢量的内在规律。语音数据是一种离散状态时序(动态离散状态)数据,对于这类问题可以使用隐马尔可夫模型解决,而HMM是一种浅层模型,对数据的建模能力有限,所以RNN应运而生。
循环神经网络(Recurrent Neural Network,RNN)以神经网络为基础,相邻隐藏层相连,因此RNN是一个循环结构,如图3.3.1所示,也就是RNN能包含之前状态的信息,它拥有一定的“记忆功能”。所以RNN对于语音这种时序信号建模尤为适合。单隐层RNN可以描述为式(3-13)和(3-14)
h t = f ( W x h x t + W h h h t − 1 ) (3-13) h_{\mathrm{t}}=\mathrm{f}\left(\mathrm{W}_{\mathrm{x} h} \mathrm{x}_{\mathrm{t}}+\mathrm{W}_{h h} h_{\mathrm{t}-1}\right)\tag{3-13} ht=f(Wxhxt+Whhht−1)(3-13)
y t = g ( W h y h t ) (3-14) \mathrm{y}_{\mathrm{t}}=\mathrm{g}\left(\mathrm{W}_{\mathrm{hy}} h_{\mathrm{t}}\right)\tag{3-14} yt=g(Whyht)(3-14)
其中, W X h W_{Xh} WXh、 W h h W_{hh} Whh和 W h y W_{hy} Why分别为输入层到隐层、隐层到隐层和隐层到输出层的权重矩阵, f ( ⋅ ) f(\cdot) f(⋅)是tanh、relu、sigmoid等激活函数, g ( ⋅ ) g(\cdot) g(⋅)是softmax等。RNN的结构如图3.3.1所示,激活函数为tanh。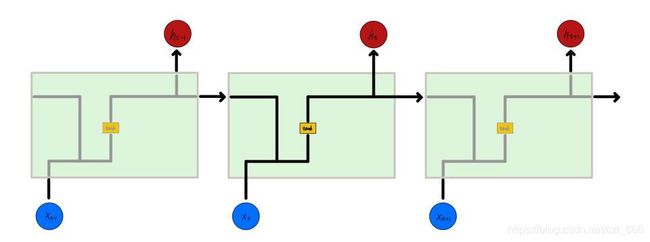 RNN存在的缺点就是存在梯度消失或梯度爆炸。为了使损失函数最小,需要反向传播更新参数,在的偏导数(3-15): ∂ e t ∂ W h h = ∑ 1 ≤ k ≤ t ∂ e t ∂ h † Π k ≤ i ≤ t ∂ h i ∂ h i − 1 ∂ + h k ∂ W h h (3-15) \frac{\partial e_{t}}{\partial W_{h h}}=\sum_{1 \leq k \leq t} \frac{\partial e_{t}}{\partial h^{\dagger}} \Pi_{k \leq i \leq t} \frac{\partial h_{i}}{\partial h^{i-1}} \frac{\partial^{+} h_{k}}{\partial W_{h h}}\tag{3-15} ∂Whh∂et=1≤k≤t∑∂h†∂etΠk≤i≤t∂hi−1∂hi∂Whh∂+hk(3-15)
RNN存在的缺点就是存在梯度消失或梯度爆炸。为了使损失函数最小,需要反向传播更新参数,在的偏导数(3-15): ∂ e t ∂ W h h = ∑ 1 ≤ k ≤ t ∂ e t ∂ h † Π k ≤ i ≤ t ∂ h i ∂ h i − 1 ∂ + h k ∂ W h h (3-15) \frac{\partial e_{t}}{\partial W_{h h}}=\sum_{1 \leq k \leq t} \frac{\partial e_{t}}{\partial h^{\dagger}} \Pi_{k \leq i \leq t} \frac{\partial h_{i}}{\partial h^{i-1}} \frac{\partial^{+} h_{k}}{\partial W_{h h}}\tag{3-15} ∂Whh∂et=1≤k≤t∑∂h†∂etΠk≤i≤t∂hi−1∂hi∂Whh∂+hk(3-15)
其中, e t e_{t} et为损失函数。
文献[11]证明了 ∥ ∏ k ≤ i ≤ t ∂ h i ∂ h i − 1 ∥ ≤ η t − k \left \| \prod_{k\le i \le t } \frac{\partial h_i}{\partial h_{i-1}} \right \| \le \eta ^{t-k} ∥∥∥∏k≤i≤t∂hi−1∂hi∥∥∥≤ηt−k,即 W h h W_{hh} Whh的偏导包含指数部分。当 η < 1 \eta <1 η<1,会出现梯度消失现象,所以RNN只能处理短期依赖(相关)的序列; η > 1 \eta >1 η>1会出现梯度爆炸,更新步子太大,超出损失函数空间范围。
3.3.2 LSTM
长短期记忆网络(Long Short-Term Memory,LSTM)是为了克服RNN的梯度消失问题而提出的。LSTM在RNN上添加遗忘门、信息增加门和输出门来控制信息流,如图3.3.2,LSTM的表达式为(3-16)到(3-20)
i t = σ ( W ( x i ) x t + W ( h i ) h t − 1 + W ( c i ) c t − 1 + b ( i ) ) (3-16) i_{t}=\sigma\left(W^{(x i)} x_{t}+W^{(h i)} h_{t-1}+W^{(c i)} c_{t-1}+b^{(i)}\right) \tag{3-16} it=σ(W(xi)xt+W(hi)ht−1+W(ci)ct−1+b(i))(3-16)
f t = σ ( W ( x f ) x t + W ( h f ) h t − 1 + W ( c f ) c t − 1 + b ( f ) ) (3-17) f_{t}=\sigma\left(W^{(x f)} x_{t}+W^{(h f)} h_{t-1}+W^{(c f)} c_{t-1}+b^{(f)}\right)\tag{3-17} ft=σ(W(xf)xt+W(hf)ht−1+W(cf)ct−1+b(f))(3-17)
c t = f t ∙ c t − 1 + i t ∙ tanh ( W ( x c ) x t + W ( h c ) h t − 1 + b ( c ) ) (3-18) c_{t}=f_{t} \bullet c_{t-1}+i_{t} \bullet \tanh \left(W^{(x c)} x_{t}+W^{(h c)} h_{t-1}+b^{(c)}\right) \tag{3-18} ct=ft∙ct−1+it∙tanh(W(xc)xt+W(hc)ht−1+b(c))(3-18)
o t = σ ( W ( x o ) x t + W ( h o ) h t − 1 + W ( c o ) c t + b ( o ) ) (3-19) o_{t}=\sigma\left(W^{(x o)} x_{t}+W^{(h o)} h_{t-1}+W^{(c o)} c_{t}+b^{(o)}\right) \tag{3-19} ot=σ(W(xo)xt+W(ho)ht−1+W(co)ct+b(o))(3-19)
h t = o t ∙ tanh ( c t ) (3-20) h_{t}=o_{t} \bullet \tanh \left(c_{t}\right)\tag{3-20} ht=ot∙tanh(ct)(3-20)
其中, i t i_t it、 f t f_t ft、 c t c_t ct、 o t o_t ot、 h t h_t ht分别表示t时刻的输入门、遗忘门、神经元激活、输出门和隐层向量。 σ ( ⋅ ) \sigma(\cdot) σ(⋅)是sigmoid函数, W W W是不同门的权重矩阵。图3.3.2为LSTM的结构图。
3.3.3 BLSTM
一个音受相邻音的影响而发生变化称为协同发音现象,系统为应对协同发音现象,一般选用上下文相关对语音建模。例如“我肚子 _ _ ,准备去吃饭。”,只有前文的判断,缺失的可能是“好痛”、“胖了”等等,上下文都有,就可以推测出缺失的为“饿了”。BLSTM(Bidirectional LSTM,双向LSTM)由双向RNN和LSTM组合。将输入数据分为前向和后向两个部分,这样不仅可以对历史信息建模,还可以对未来信息建模。显然BLSTM比LSTM具有更好的识别效果,BLSTM网络结构图3.3.3所示。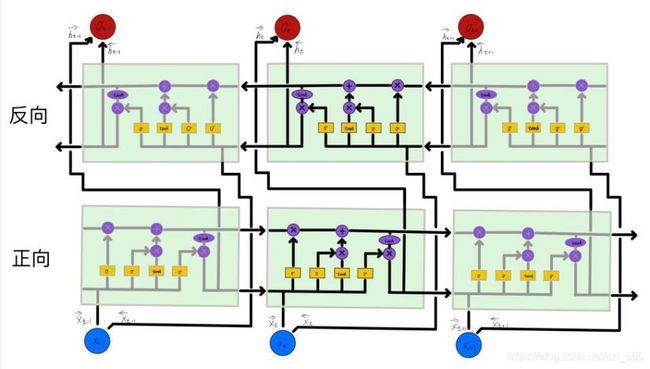
四、CTC
4.1 CTC解码
通常构建损失函数训练时需要将音频和标签字符一一对齐,人工逐帧对齐需要花费大量的时间,并且预测的结果不是整个序列的输出结果,联结主义时序分类器(Connectionist Temporal Classification,CTC)提供了可行的解决方案。给定输入序列 x x x,最大化后验概率 p ( o ∣ x ) p(o\mid x) p(o∣x),其中 o o o为输出序列,输入到输出的映射称为转录。首先研究完全正确的转录,即 p ( o ∣ x ) = 1 p(o\mid x)=1 p(o∣x)=1,由于人说话发音是连续的,相邻语音帧输出重复的字符,需要去重,并且由于每个人的说话速度不同或者字符间隔距离不同,导致 x x x和 o o o有多种转录关系,多种转录都对应着相同的,如式(4-2)所示,因此可以设计一个B变换将 o o o映射到 l l l。
p ( l ∣ x ) = ∑ o ∈ B − 1 ( l ) p ( o ∣ x ) (4-2) p(l \mid x)=\sum_{o \in B^{-1}(l)} p(o \mid x)\tag{4-2} p(l∣x)=o∈B−1(l)∑p(o∣x)(4-2)
式中表示将输出序列经过B变换映射到标签序列。因此,只需要穷举搜索满足B变换所有的输出序列 o o o。然而对于每一个标签序列都穷举所有的输出序列,计算复杂度是指数级的,搜索空间太大,训练速度必然非常缓慢。穷举搜索类似于HMM的解码问题,CTC相当于HMM的扩展形式,图4.1.1为解码成“hello”的时序状态图。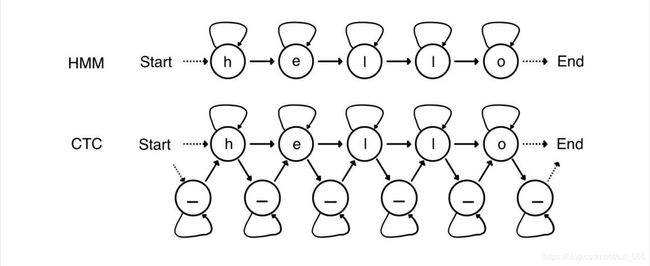 通过在HMM每个状态之间插入一个空格(blank)状态,在图4.1.1中将空格状态定义为符号“_”,空格状态和非空状态都有一个自旋。搜索空间就可由包含空格的标签和时间序列组成,每个小圆圈表示状态,箭头表示状态转移。扩展的标签经过B转换后映射到标签上,B转换需满足如下约束:状态之间的转换,只能往右或者右下方向;相同的字符中间必须要有空格blank;非空字符不可被跳过;起点只能从第一个时间片的前两个开始;终点只能落在最后一个时间片的后两个。图4.1.2为标签“”的搜索空间,其中绿色的路径表示满足B变换约束条件的路径。
通过在HMM每个状态之间插入一个空格(blank)状态,在图4.1.1中将空格状态定义为符号“_”,空格状态和非空状态都有一个自旋。搜索空间就可由包含空格的标签和时间序列组成,每个小圆圈表示状态,箭头表示状态转移。扩展的标签经过B转换后映射到标签上,B转换需满足如下约束:状态之间的转换,只能往右或者右下方向;相同的字符中间必须要有空格blank;非空字符不可被跳过;起点只能从第一个时间片的前两个开始;终点只能落在最后一个时间片的后两个。图4.1.2为标签“”的搜索空间,其中绿色的路径表示满足B变换约束条件的路径。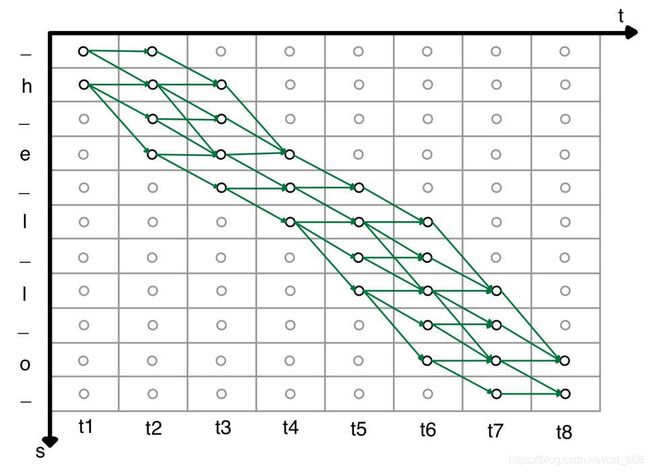
HMM解码问题可以用Viterbi算法解决,CTC也可以。将路径集合分为前向和后向部分。在时刻t经过s的全部前向子路径概率之和为前向概率 a t ( s ) a_{t}(s) at(s),其数学表达式为(4-3)~(4-6)。前向概率:
α t ( s ) = ∑ e ∈ B − 1 ( I ) p ( o 1 : t ∣ x ) α 1 ( l ) = y t l , α l ( 2 ) = y i 2 l , α l ( s ) = 0 , ∀ s > 2 a t ( s ) = 0 , ∀ s < l ∣ + 2 ( T − t ) − 1 α t ( s ) = { α t ( s ) = ( α t − 1 ( s ) + α t − 1 ( s − 1 ) ) ⋅ y i s t , if I s = b or i s − 2 = 1 ( α t − 1 ( s ) + α t − 1 ( s − 1 ) + α t − 1 ( s − 2 ) ) ⋅ y i t , otherwise (4-3:4-6) \begin{aligned}\tag{4-3:4-6} &\alpha_{t}(s)=\sum_{e \in B^{-1}(I)} p\left(o_{1: t} \mid x\right) \\ &\alpha_{1}(l)=y_{t}^{l}, \alpha_{l}(2)=y_{i_{2}}^{l}, \alpha_{l}(s)=0, \forall s>2 \\ &a_{t}(s)=0, \forall s
在时刻t经过s的全部后向子路径概率之和为前向概率,其数学表达式为(4-7)~(4-10)。后向概率:
β t ( s ) = ∑ o ∈ B − 1 ( l ) p ( o t : T ∣ x ) β T ( ∣ l ′ ∣ ) = y − T , β T ( ∣ l ′ ∣ − 1 ) = y i i ∣ − 1 T , β T ( s ) = 0 , ∀ s > ∣ l ′ ∣ − 1 β t ( s ) = 0 , ∀ s > 2 t , ∀ s > ∣ l ′ ∣ β t ( s ) = { a t ( s ) = ( β t + 1 ( s ) + β t + 1 ( s + 1 ) ) ⋅ y i t , if ∣ s = b or l s + 2 = I s ( a t − 1 ( s ) + a t − 1 ( s − 1 ) + a t − 1 ( s − 2 ) ) ⋅ y i , s t , otherwise (4-7:4-10) \begin{aligned}&\beta_{t}(s)=\sum_{o \in B^{-1}(l)} p\left(o_{t: T} \mid x\right)\\ &\beta_{T}(|l'|)=y_{-}^{T}, \beta_{T}(|l'|-1)=y_{i_{i \mid-1}}^{T}, \beta_{T}(s)=0, \forall s>|l'|-1\\ &\beta_{t}(s)=0, \forall s>2 t, \forall s>|l'|\\ &\beta_{t}(s)=\left\{\begin{array}{c}a_{t}(s)=\left(\beta_{t+1}(s)+\beta_{t+1}(s+1)\right) \cdot y_{i}^{t}, \quad \text { if }\left.\right|_{s}=b \text { or } l_{s+2}=I_{s} \\ \left(a_{t-1}(s)+a_{t-1}(s-1)+a_{t-1}(s-2)\right) \cdot y_{i, s}^{t}, \text { otherwise }\end{array}\right.\end{aligned}\tag{4-7:4-10} βt(s)=o∈B−1(l)∑p(ot:T∣x)βT(∣l′∣)=y−T,βT(∣l′∣−1)=yii∣−1T,βT(s)=0,∀s>∣l′∣−1βt(s)=0,∀s>2t,∀s>∣l′∣βt(s)={at(s)=(βt+1(s)+βt+1(s+1))⋅yit, if ∣s=b or ls+2=Is(at−1(s)+at−1(s−1)+at−1(s−2))⋅yi,st, otherwise (4-7:4-10)
因此在任意的t时刻,遍历所有的s,即将得到全部路径的概率总和表示为式(4-11):
p ( l ∣ x ) = ∑ s = 1 ∣ l ′ ∣ a t ( s ) β t ( s ) y l s ′ t (4-11) p(l\mid x)=\sum_{s=1}^{|l'|} \frac{a_{t}(s) \beta_{t}(s)}{y_{l_{s}'}^{t}}\tag{4-11} p(l∣x)=s=1∑∣l′∣yls′tat(s)βt(s)(4-11)
给定一个目标转录,CTC的目标函数为:
CTC ( x ) = − log p ( l ∗ ∣ x ) (4-12) \text { CTC }(x)=-\log p\left(l^{*} \mid x\right)\tag{4-12} CTC (x)=−logp(l∗∣x)(4-12)(4-12)
4.2转录损耗
上面提到的CTC的目标函数是正确转录的对数概率,不正确转录的概率容易被忽视。在此引入编辑距离,编辑距离是用来度量两个序列之间的相似程度,通俗的说就是将一个序列转换到另一个序列所需的编辑操作次数,其中一次只能编辑一个字符。序列的转换简称为转录,当转录所需编辑操作次数为零时,即表示正确转录,同理,当转录编辑操作次数不为零时,就是我们关注的不正确转录。转录序列就是经过编辑操作的输出序列,所以转录序列服从。将实值转录损耗函数定义为,则转录损耗期望可表示为(4-13)。
L ( x ) = ∑ y p ( x ∣ y ) ⋅ L ( x , y ) = ∑ y ∑ o ∈ B − 1 ( l ) , o t = l s ′ p ( 0 ∣ y ) ⋅ L ( x , y ) = ∑ o p ( o ∣ x ) ⋅ L ( x , B ( o ) ) (4-13) \begin{aligned}L(x) &=\sum_{y} p(x \mid y) \cdot L(x, y) \\&=\sum_{y} \sum_{o \in B^{-1}(l) ,o_t=l_s'} p(0 \mid y) \cdot L(x, y) \\&=\sum_{o} p(o \mid x) \cdot L(x, B(o))\end{aligned}\tag{4-13} L(x)=y∑p(x∣y)⋅L(x,y)=y∑o∈B−1(l),ot=ls′∑p(0∣y)⋅L(x,y)=o∑p(o∣x)⋅L(x,B(o))(4-13)
由于后验概率分布太过复杂,所以无法精确的求解期望。根据大数定理,期望约等于均值,可以用MCMC(Markov Chain Monte Carlo,蒙特卡洛马尔可夫链)来近似 [ 16 ] ^{[16]} [16]。Markov链能收敛至某一个平稳分布,一般平稳分布比目标函数要简单的多,所以可以设计一个马尔可夫链的转移矩阵来近似目标函数,然后在平稳分布上进行采样作为函数的输入即可近似L,如下(4-14)所示。 L ( x ) = E [ L ( x , B ( o ) ) ] ≈ 1 N ∑ n = 1 N L ( x , B ( o i ) ) , o i ∼ p ( o ∣ x ) (4-14) \begin{aligned}L(x) &=E[L(x, B(o))] \\& \approx \frac{1}{N} \sum_{n=1}^{N} L\left(x, B\left(o^{i}\right)\right), o^{i} \sim p(o \mid x)\end{aligned}\tag{4-14} L(x)=E[L(x,B(o))]≈N1n=1∑NL(x,B(oi)),oi∼p(o∣x)(4-14)
[1] DAVIS K.H,BIDDULPH R,BALASHEK S.Automatic recognition of spoken digits[J].Journal of the Acoustical Society of America,1952,24(6):637.
[2] FERGUSON J D.Application of hidden Markov models to text and speech[EB].1980.
[3] RABINER L R.A tutorial on hidden Markov models and selected applications in speech recognition[J].Readings in Speech Recognition,1990,77(2):267-296.
[4] LEEE K F L M.An overview of the SPHINX speech recognition system[J].IEEE Transactions on Acoustics Speech & Signal Processing Speech,1990,38(1):35-45.
[5] 韩纪庆,张磊,郑铁然.语音信号处理[M].北京:清华大学出版社,2004.
[6] WAIBEL A,HANAZAWA T,HINTON G.Phoneme recognition using time-delay neural networks[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1990,1(2):393-404.
[7] HINTON G E,OSINDERO S,TEH Y W.A fast learning algorithm for deep belief nets[J].Neural Computation,2006,18(7):1527-1554.
[8] MOHAMED A R,DAHL G,HINTON G.Deep belief networks for phone recognition[EB].2009.
[9] 俞栋(美),邓力(美)著.俞凯等译.解析深度学习:语音识别实践[M].北京:电子工业出版社,2016.
[10] Wang D,Zhang X.THCHS-30:A Free Chinese Speech Corpus[J].Computer Science, 2015.
[11] Pascanu R , Mikolov T , Bengio Y . On the difficulty of training Recurrent Neural Networks[J]. 2012.
[12] HOCHREITER S,SCHMIDHUBER J.Long short-term memory[J].Neural Computation,1997.
[13] Shiliang Zhang,Cong Liu,Hui Jiang,Si Wei,Lirong Dai,Yu Hu.Feedforward Sequential Memory Networks:A New Structure to Learn Long-term Dependency.[J].Computer Science,2015.
[14] 蒋俊正.DFT调制滤波器组的设计算法研究[D].西安电子科技大学,2011.[15] 薛少飞. DNN-HMM语音识别声学模型的说话人自适应[D].中国科学技术大学,2015.
[16] 曹小群,宋君强,张卫民,赵军,张理论.MCMC方法在生物逆问题求解中的应用.国防科学技术大学 计算机学院,长沙 410073.
[17] 刘盈.大词表连续语音识别识别系统的研究与实现[D].北京:清华大学,2005.