人工智能2—感知机算法

感知机（Perceptron ）算法

目录

 

1.简介

2.原理

2.1.感知机模型

2.2.学习策略——损失函数

2.3.算法步骤

2.4.优缺点

3.常用的优化算法

1.批量梯度下降（BGD）

2.随机梯度下降（SGD）

3.随机批量梯度下降★

---

1.简介

感知机（Perceptron ），是Frank Rosenblatt在1957年就职于Cornell航空实验室时所发明的一种人工神经网络，被视为一种最简单形式的前馈式人工神经网络，是一种二元线性分类器。

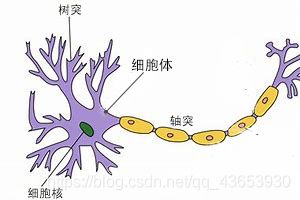
感知器是生物神经细胞的简单抽象，如下图1示神经细胞结构大致可分为：树突、轴突，突触及细胞体。

                            图1

神经细胞的状态取决于从其它的神经细胞收到的输入信号量，及突触的强度。当信号量总和超过了某个阈值时，细胞体就会激动，产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。为了模拟神经细胞行为，与之对应的感知机基础概念被提出，如图2权量（突触）、偏置（阈值）及激活函数（细胞体），一个由输入空间x到输出空间f(x)的函数，w(w1,w2,...,wn)就是权值，表示各个输入对于输出的重要程度。

                          图2

2.原理

2.1.感知机模型

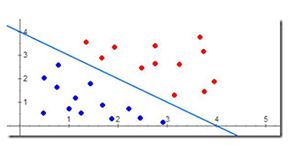
感知机模型是一个线性分类器，它的目标是通过训练数据将数据集进行线性二分类，也就是在数据集线性可分的情况下，感知机的目标就是通过已知数据训练出一个超平面，类似于一个y=kx+b的线性函数如图3所示，这个超平面可以将两类样本点完全

                          图3

正确分类，找到这个超平面其实就是确定感知机模型参数w、b。

感知机模型就是：f(x)=sign(wx+b)

w为权值，b为偏置（或阈值）（用来调整整体结果和阈值之间的关系），sign为符号函数：

感知机模型的原理就是每一个参数值就对应一个目标模型，先初始化参数，然后根据已知数据判断这个模型是否符合我们的期望，如果不符合，就要根据感知机的学习策略来更新参数，以此来得到新模型，再判断是否符合，以此类堆不断循环直到得到符合期望的模型。

2.2.学习策略——损失函数

要确定感知机的学习策略，其实就是定义一个损失函数，来衡量目标模型的优劣，损失函数极小化的过程就是目标模型优化的过程，因此求解目标模型就转化成了求解损失函数的最小值。

损失函数：L(w,b)=-∑ yi(w*xi+b)

为第i组的输入和输出，(w*xi+b)是根据当前模型对x做的预测值，yi是对应于xi的真实值，当一个样本分类正确时（即阈值b为0，预测值和真实值都大于0或小于0），它的输出是负值；分类错误时，输出值是正值。

先初始化一组参数，即初始化一个超平面，然后通过梯度下降法不断地优化目标函数，也就是对损失函数L(w,b)=-∑ yi(w*xi+b)分别对w、b分别求偏导，以求出损失函数最小值：

                               误分类点

随机选取一个误分类点(xi,yi)，对w和b进行更新：

   

η 为学习率，η越大，需要更新的次数越少，这样不断迭代可以使得损失函数L(w,b)不断减小，直到为0。

2.3.算法步骤

输入：训练数据T={(x1,y1),(x2,y2),...,(xn,yn)}，学习率η 

输出：w，b，感知机模型f(x)=sign(wx+b)

1. 初始化参数w0，b0
2. 依次选取训练数据(xi,yi)
3. 如果yi(w*xi+b)<=0，即分类错误，使用随机梯度下降法更新w和b
4. 转到第2步，循环直到训练数据的所有样本点全部被分类正确

2.4.优缺点

（1）优点：系统结构简单，模型易于训练，对于二分类问题效果显著，算法高效。

（2）缺点：不能解决线性不可分问题；面向二分类任务，对于对分类的任务只能简单地转换为多个二分类问题来处理。

3.常用的优化算法

1.批量梯度下降（BGD）

批量梯度下降法是指在每次迭代时使用所有样本来进行梯度更新。

2.随机梯度下降（SGD）

随机梯度下降是指每次迭代时使用一个样本来进行梯度更新，只通过一个随机选取的数据(xi,yi) 来获取“梯度”来对w 进行更新。

3.随机批量梯度下降★

又叫小批量梯度下降（MBGD），是批量梯度下降和随机梯度下降的一个折中方法，每次迭代使用batch_size个样本来对参数进行更新。每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降结果。