吴恩达机器学习总结(三)——神经网络的反向传播
神经网络的反向传播
在上一篇博客中,利用神经网络对手写数字数据进行分类的结果虽然已经很高了,但和测试样本本身的输出值进行比较还是存在着一定的误差。这时我们需要使用这个误差值来调整神经网络本身,进而改变神经网络的输出值。
误差传递
我们知道在前向传播中,每个节点向下一层传递的信号所占权重不同。若只有一个节点的信号传递到输出节点,那调整神经网络输出值的方式将简单的多,只需要更新这个节点的权重即可。假如有多个节点时,我们就不能仅仅对其中一个节点的权重进行更新了,这么做忽略了其他链接及其权重,因为可能多条链接都对误差值有所影响。可能对于权重较大的链接,它对误差的影响相比于权重较小的链接要来着大,所以我们可以利用这种方式,根据给个链接的权重大小来分配误差。在前向传播中,我们使用权重将信号从输入层传播到输出层,而现在,我们使用权重,让输出层的误差向后传播到各个节点上,然后在更新各个节点的权重,使得误差最小,这种方法称为反向传播。

上图是一个两层的浅层神经网络,具有两个输出值,反向传播的流程在图中用蓝色和红色(可能不是很明显)箭头标出了。
e 01 e_{01} e01和 e 02 e_{02} e02都是模型输出值和真实值之间的误差,这是可以直接计算得出的。
e h 1 e_{h1} eh1是神经网络隐藏层的c节点的误差值。但是在隐藏层中,我们的数据并没有给出具体的输出值,那么隐藏层中的误差是怎么求的?c节点具有两个链接,分别链接着两个输出节点,每个链接在传递信号时都存在着一定的误差,所以我们可以重组这两个链接上的误差,形成c节点的误差。但这个误差并不等于目标输出值和实际输出值的差,因为样本只在最终输出层中给出了实际的值,并没有告诉我们其他层节点的输出应该是多少。
利用误差的方向传播,为链接重组误差。c节点的误差是与这个节点向前传播所有链接中分割误差的和:

隐藏层第二个节点d同理:

写成矩阵相乘的形式就是:

这里去掉了分母,这些分数的分母其实是一种归一化因子,去除之后不影响误差之间比例。简写如下:
e r r o r h i d d e n = [ w 11 w 12 w 21 w 22 ] [ e o 1 e o 2 ] error_{hidden}=\begin{bmatrix}w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix}\begin{bmatrix}e_{o1} \\ e_{o2}\end{bmatrix} errorhidden=[w11w21w12w22][eo1eo2]
用矩阵的方法表示:
e r r o r h i d d e n = w T ⋅ e r r o r o u t p u t error_{hidden}=w^T·error_{output} errorhidden=wT⋅erroroutput
w T w^T wT就是这一层的权重矩阵的转置。权重矩阵在向前传播和向后传播中都扮演着重要的角色,在向前传播中权重矩阵实现在输入层→隐藏层→输出层之间传递信号,在向后传播中,权重矩阵实现在输出层→隐藏层→输入层之间传递误差。
更新权重
我们在误差的向后传递中,得到了每个节点的误差,将根据这个误差来更新每个节点的权重。反向传播算法的目标是更新神经网络中的每一个权重,以便得到实际输出和目标输出更接近,因此要最小化输出节点和整个网络的误差,试图优化的参数是神经网络的权重参数。对此,我们采用梯度下降的方法来实现。
在此之前,先了解一个表达式的含义: d E d w \frac {dE}{dw} dwdE这个表达式意思是:当权重w改变时,误差E是如何变化的,也就是误差函数的斜率。我们通过链式反应将这个表达式拆解开:
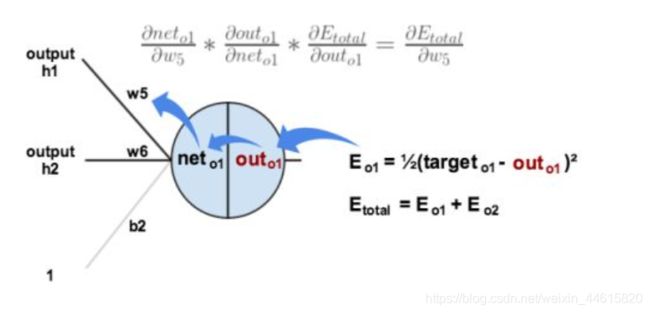
上图是在输出层,权重参数 w 5 w_5 w5是如何影响误差E的示意图, σ 和 d \sigma 和d σ和d都是导数符号,大小写不同而已。这是在输出层误差的具体传递步骤。
通过链式法则可以将 d E t o t a l d w 5 \frac {dE_{total}}{dw_5} dw5dEtotal分为三个步骤 d E t o t a l d w 5 = d E t o t a l d o u t o 1 ∗ d o u t o 1 d n e t o 1 ∗ d n e t o 1 d w 5 \frac {dE_{total}}{dw_5}=\frac {dE_{total}}{dout_{o1}}*\frac {dout_{o1}}{dnet_{o1}}*\frac {dnet_{o1}}{dw_5} dw5dEtotal=douto1dEtotal∗dneto1douto1∗dw5dneto1
总误差到输出层其中一个节点的误差: d E t o t a l d o u t o 1 \frac {dE_{total}}{dout_{o1}} douto1dEtotal,总误差 E t o t a l = 1 2 ( t a r g e t o 1 − o u t o 1 ) 2 + 1 2 ( t a r g e t o 2 − o u t o 2 ) 2 E_{total}=\frac {1}{2}(target_{o1}-out_{o1})^2+\frac {1}{2}(target_{o2}-out_{o2})^2 Etotal=21(targeto1−outo1)2+21(targeto2−outo2)2,代入表达式里求导就是 d E t o t a l d o u t o 1 = − ( t a r g e t o 1 − o u t o 1 ) \frac {dE_{total}}{dout_{o1}}=-(target_{o1}-out_{o1}) douto1dEtotal=−(targeto1−outo1)
激活函数到线性函数的误差: d o u t o 1 d n e t o 1 \frac {dout_{o1}}{dnet_{o1}} dneto1douto1,就是 g ′ ( z ) g'(z) g′(z),不同的激活函数的导函数不同,对于sigmoid函数: d o u t o 1 d n e t o 1 = o u t o 1 ( 1 − o u t o 1 ) \frac {dout_{o1}}{dnet_{o1}}=out_{o1}(1-out_{o1}) dneto1douto1=outo1(1−outo1)
线性函数的误差: d n e t o 1 d w 5 \frac {dnet_{o1}}{dw_5} dw5dneto1,对线性函数求导,即上一层该权重对应的激活函数的输出值 d n e t o 1 d w 5 = o u t p u t h 1 \frac {dnet_{o1}}{dw_5}=output_{h1} dw5dneto1=outputh1
最后结合起来:
d E t o t a l d w 5 = − ( t a r g e t o 1 − o u t o 1 ) ∗ o u t o 1 ∗ ( 1 − o u t o 1 ) ∗ o u t p u t h 1 \frac {dE_{total}}{dw_5}=-(target_{o1}-out_{o1})*out_{o1}*(1-out_{o1})*output_{h1} dw5dEtotal=−(targeto1−outo1)∗outo1∗(1−outo1)∗outputh1
我们用梯度下降更新权重的方式为: w : = w − α d w w := w-\alpha dw w:=w−αdw式中的 α \alpha α是学习率,也就会梯度下降的步长。
对于隐藏层的误差传播,步骤和输出层类似,不同的就是每个隐藏节点的输出都会对多个输出神经元和误差有影响,所以在计算的时候需要这个情况考虑进去。
向量化
当有m个训练样本,为了加快程序运行效率,最好采用向量化的方法,向量化整个计算。




我们用X代表输入的样本,形成n乘m维的矩阵,其中的n是代表特征数,m是样本数。 x ( 1 ) , x ( 2 ) 等 等 都 是 x ( m ) x^{(1)},x^{(2)}等等都是x^{(m)} x(1),x(2)等等都是x(m)的列向量(共有n个),将这些列向量都组合在一个矩阵X中,就可以遍历所有样本和所有特征。
同理, z [ 1 ] ( 1 ) , z [ 1 ] ( 2 ) z^{[1](1)},z^{[1](2)} z[1](1),z[1](2)等等都是 z [ 1 ] ( m ) z^{[1](m)} z[1](m)的列向量,将所有m都组合在各列中,就得到矩阵 z [ 1 ] z^{[1]} z[1]。
同理, a [ 1 ] ( m ) , a [ 1 ] ( m ) , . . . a [ 1 ] ( m ) a^{[1](m)},a^{[1](m)},...a^{[1](m)} a[1](m),a[1](m),...a[1](m)将其组合在矩阵各列中就能得到矩阵 a [ 1 ] a^{[1]} a[1]。
方括号中的数字表示的是具体层数,如[1]表示的是第一层。对于 z [ 2 ] z^{[2]} z[2]和 a [ 2 ] a^{[2]} a[2]也是这样得到的,对于不同层有 z [ l ] z^{[l]} z[l]和 a [ l ] a^{[l]} a[l],l表示层数,从1至L。 z [ l ] z^{[l]} z[l]和 a [ l ] a^{[l]} a[l]在水平方向上遍历所有样本,在垂直方向上遍历的是该层的所有节点 n [ l ] n^{[l]} n[l](神经元),其维度是 ( n [ l ] , m ) (n^{[l]},m) (n[l],m)。
使用向量化的的方法,在编写程序中可以不需要对各个样本使用显式for循环,只需要对层数L使用for循环(假如层较多的话)。我们可以直接通过矩阵运算,从X计算得出 A [ 1 ] A^{[1]} A[1], Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]} Z[2]=W[2]A[1]+b[2],需注意的是这里的W,b也是一个矩阵,维度分别是 ( n [ l ] , n [ l − 1 ] ) (n^{[l]},n^{[l-1]}) (n[l],n[l−1])和 ( n [ l ] , 1 ) (n^{[l]},1) (n[l],1)。
在实际计算值,确保维度的准确是很重要的,以 Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]} Z[2]=W[2]A[1]+b[2]为例:
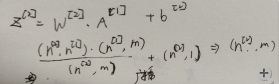
W [ 2 ] W^{[2]} W[2]的维度是 ( n [ 2 ] , n [ 1 ] ) (n^{[2]},n^{[1]}) (n[2],n[1]), A [ 1 ] A^{[1]} A[1]的维度是 ( n [ 1 ] , m ) (n^{[1]},m) (n[1],m), b [ 2 ] b^{[2]} b[2]的维度是 ( n [ 2 ] , 1 ) (n^{[2]},1) (n[2],1),由于python广播的关系,当 ( n [ l ] , m ) (n^{[l]},m) (n[l],m)的矩阵与 ( n [ l ] , 1 ) (n^{[l]},1) (n[l],1)的矩阵进行基本运算时,会将 ( n [ 2 ] , 1 ) (n^{[2]},1) (n[2],1)的矩阵与前者相对应,这里就是乘以了m,最后得出结果为 ( n [ 2 ] , m ) (n^{[2]},m) (n[2],m)与 Z [ 2 ] Z^{[2]} Z[2]的维度相一致。
在反向传播中, d w [ l ] dw^{[l]} dw[l]与 w [ l ] w^{[l]} w[l]的维度是相一致的,都为 ( n [ l ] , n [ l − 1 ] ) (n^{[l]},n^{[l-1]}) (n[l],n[l−1]); d b [ l ] db^{[l]} db[l]与 b [ l ] b^{[l]} b[l]的维度是相一致的,为 ( n [ l ] , 1 ) (n^{[l]},1) (n[l],1)。
随机初始化
在神经网络中,如果把权重参数都初始化为0,那么梯度下降将不再起到作用。举个例子:

若把权重参数矩阵 W [ 1 ] , W [ 2 ] W^{[1]},W^{[2]} W[1],W[2]都设为0,这时就存在一个问题,那就是 a 1 [ 1 ] a_1^{[1]} a1[1]和 a 2 [ 1 ] a_2^{[1]} a2[1]都相等了,因为两个链接计算的是相同的函数。如果这么将神经网络的权重矩阵都初始化为0,那么隐藏单元就会完全一样,每个节点都接收相同的信号并且输出值也是相同的。在反向传播误差时,由于每个节点的权重相同,所以误差也会得到平分,这将导致相同的权重更新,这是毫无意义的。
因此,在初始化权重时,我们可以另其等于一个很小的数,如:

总结就是:
W [ l ] = n p . r a n d o m . r a n d n ( n [ l ] , n [ n − 1 ] ) ∗ 0.01 W^{[l]}=np.random.randn(n^{[l]},n^{[n-1]})*0.01 W[l]=np.random.randn(n[l],n[n−1])∗0.01
b [ l ] = n p . z e r o s ( ( n [ l ] , 1 ) ) b^{[l]}=np.zeros((n^{[l]},1)) b[l]=np.zeros((n[l],1))