FFT matlab实现以及应用分析

FFT实现

此处内容引用某篇博客，懒得找了，对此FFT的matlab实现讲的十分详细，大家想找的话可以自己去找

按时间抽取的信号流图：

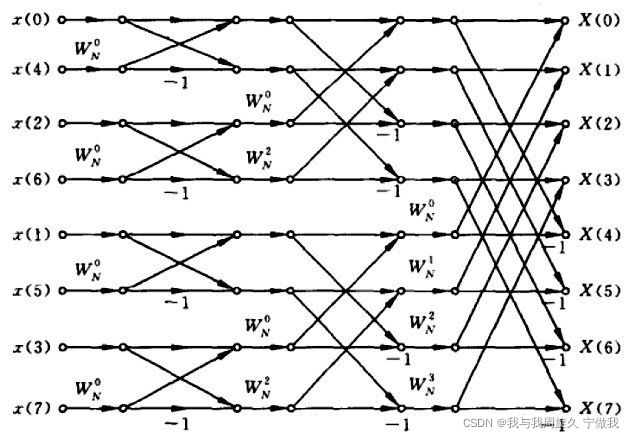
我们从这张信号流图可以抽象出程序的实现步骤：首先对信号时间序列进行逆序处理，再进行下面的工作，分三层循环进行：
第一个循环是进行N阶的FFT运算；第二个循环其实就是，每一阶FFT的时候，有多少组DFT对象，拿8点来说，第一阶的时候，有4组DFT对象，到了第二阶，就有2组，到了第三，就是最后一阶，只有一组；第三个循环，其实是在每一组DFT里边，执行多少次蝶形运算！8点FFT来说，第一阶每组有一个蝶形，第二阶每组有2个，第三阶每组有4个蝶形。
具体流程图如下：

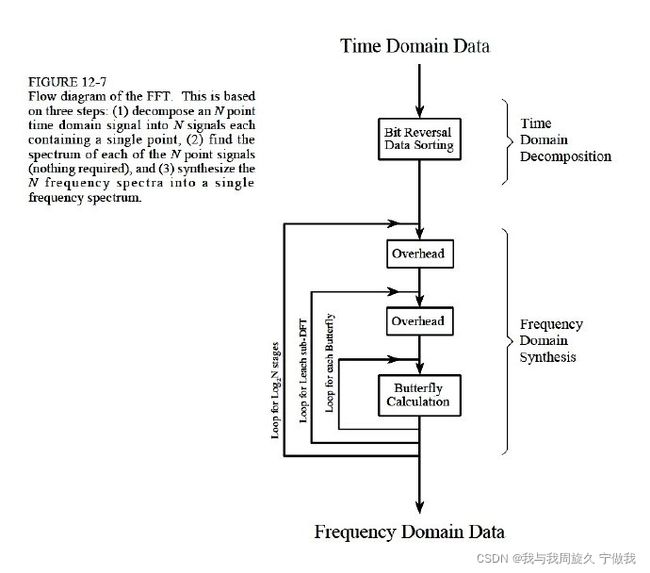
i , j, k 三者，反别表示三层循环，然后得出循环次数的关系：
stages = log2(PointNum)，i从0到stage-1，j从0 到2^(stages - (i + 1)) – 1，k 从0到2^i – 1。
下面是进行蝶形运算的流程：
首先确定旋转因子W，根据8点DIT-FFT图，得到相关表达式
然后是具体蝶形计算的实现，我们在计算机里面操控的都是实数，所以将其分为实部虚部两部分计算来弄：
在完成相关的代码编程后，用以下的时间序列做实验：


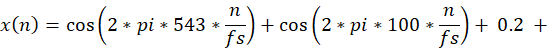
fs取1024*2,取样点数N取512，最终得到的结果如下：

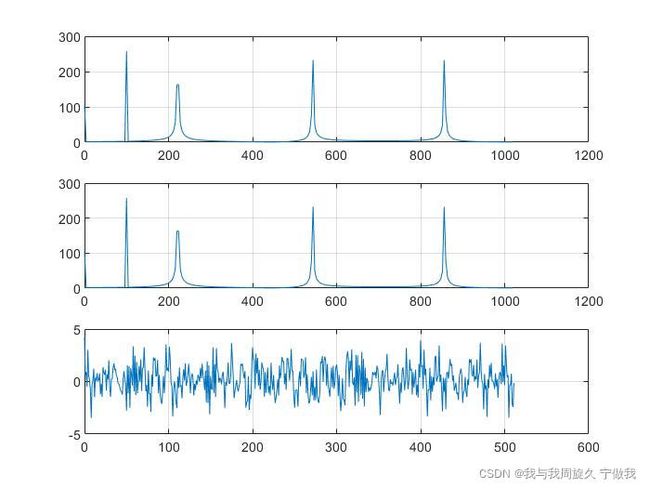
第一幅图为matlab自带的fft，第二幅图是编写的fft，其中纵坐标为幅值，横坐标的单位为fs/N（频率分辨率），而且由于fft的对称性，以及奈奎斯特采样定律（fs大于采样序列中最大频率的两倍），故只展示了前半部分的频域图。第三章图为时域图。
从上面的图中我们可以看到，频率分量都被很好的提取了出来，但是幅值方面似乎不是太对，经过查阅资料，我发现：要想恢复幅值，首先FFT求出来的幅值要乘2/N（直流分量不用乘2），其次N与fs要有个对应关系：N为fs的整数倍（即不发生频谱泄露）。
处理后的效果图：

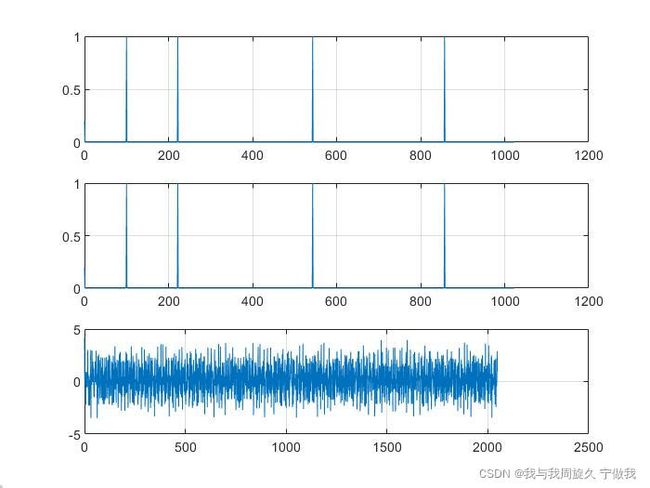
可以看到它可以完美的还原出原信号。
但是我们在实际中通常是非周期截断（N不是fs整数倍）。

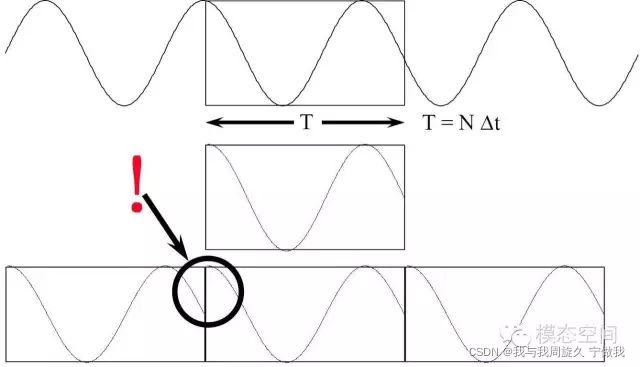
截断后的信号起始时刻和结束时刻的幅值明显不等，将这个信号再进行重构，在连接处信号的幅值不连续，出现跳跃，如图中黑色圆圈区域所示。
对截断后的信号做FFT分析，得到的频谱如下图所示。

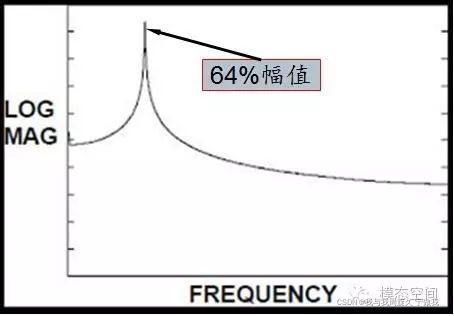
这时的FFT频谱已远远不是我们预期的那种单条离散谱线了（周期截取的频谱样子）。对比周期截断的频谱，可以看出，此时频谱在整个频带上发生“拖尾”现象。峰值处的频率与原始信号的频率相近，但并不相等。另一方面，峰值处的幅值已不再等于原始信号的幅值，为原始信号幅值的64%（矩形窗的影响）。而幅值的其他部分（36%幅值）则分布在整个频带的其他谱线上。由于信号的非周期截断，导致频谱在整个频带内发生了拖尾现象。这是非常严重的误差，称为泄漏，是数字信号处理所遭遇的最严重误差。
 
对比一下正确的频谱与发生泄漏的频谱，如下图所示，

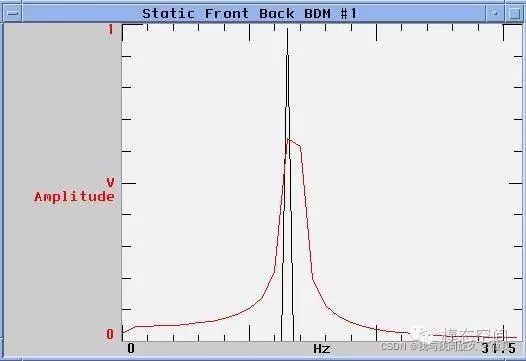
可以看出，泄漏后的频谱的幅值更小，频谱拖尾更严重。当截断后的信号不为周期信号时，就会发生泄漏。而现实世界中，在做FFT分析时，很难保证截断的信号为周期信号，因此，泄漏不可避免。
现在返回到非周期截断的正弦波，可以看出在截断时间长度内没有捕捉到整数倍个周期正弦波，导致波形发生了失真，似乎在信号周期的末端波形出现了不连续。这就解释了为什么FFT会在整个频带上发生拖尾现象了。本质上，这需要多个傅立叶展开项（多条谱线）去近似这个明显不连续的信号，因此，频谱出现了拖尾现象。
为了将这个泄漏误差减小到最小程度，我们需要使用加权函数，也叫窗。加窗主要是为了使信号更好地满足FFT处理的周期性要求，减少泄漏。如下图所示：

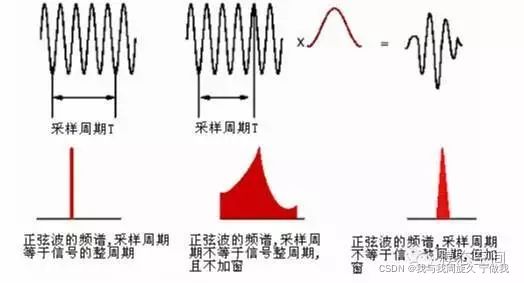
若周期截断，则FFT频谱为单一谱线。若为非周期截断，则频谱出现拖尾，如图中部所示。为了减少泄漏，给信号施加一个窗函数（如图中红色曲线所示），原始截断后的信号与这个窗函数相乘之后得到的信号为右侧上面的信号。可以看出，此时，信号的起始时刻和结束时刻幅值都为0，也就是说在这个时间长度内，信号为周期信号，但是只有一个周期。对这个信号做FFT分析，得到的频谱如右侧下边所示。相比较之前未加窗的频谱，可以看出，泄漏已明显改善，但并没有完全消除泄漏。因此，窗函数只能减少泄漏，不能消除泄漏。

利用FFT进行声音处理

首先利用audioread读入声音。时域波形如下：

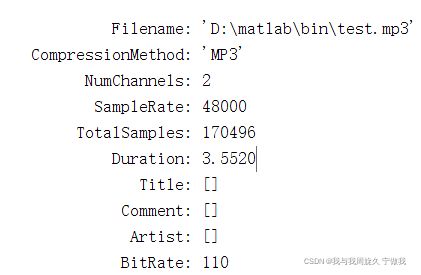
关于这段音频的信息如下：

利用FFT进行分析，得到的频谱如下：

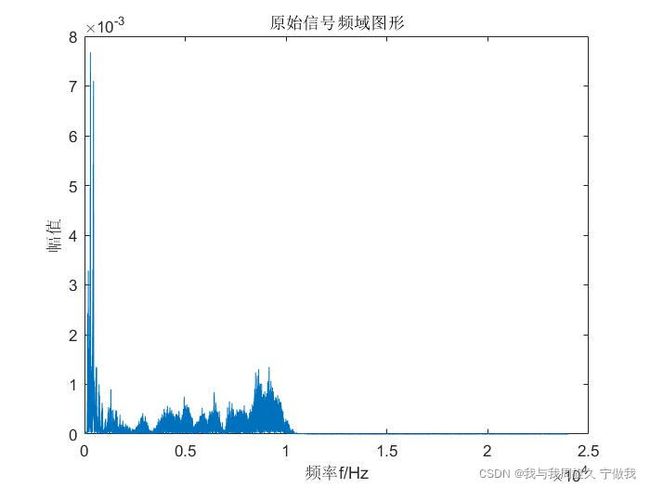
根据图10我们可以知道，采样频率为48000，采样点数为170496
我们首先对利用matlab的randn声音进行加噪处理，加噪后的波形如下：

由两个频域图对比可知，噪声主要集中在高频部分，所以我们设计一个低通滤波器，去除噪声同时最大程度保留源信号。利用firl函数设计，其中参数如下：
fp=1500;fc=1700;As=100;Ap=1;
得到的滤波伯德图如下：

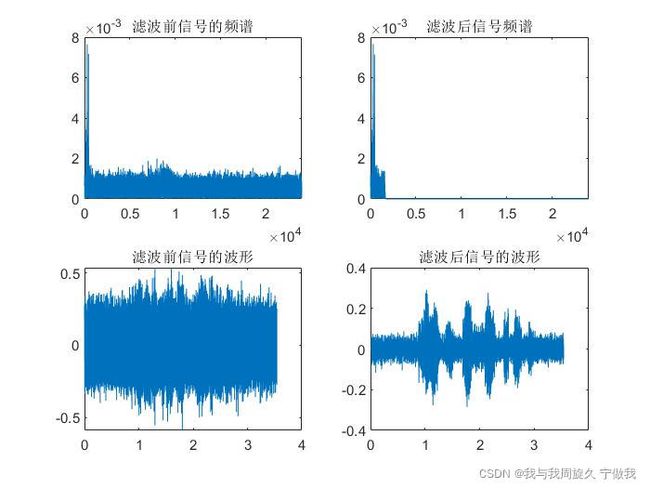
最后利用fftfilt滤波后的效果对比图如下：

代码附录

一、FFT的部分
PointNum  = 1024*2;
PointBitNum =11;
fs = 1024*2;
n = 0:1:PointNum - 1;
sampletab = cos(2*pi*543*n/fs) + cos(2*pi*100*n/fs) + 0.2 + cos(2*pi*857*n/fs) + cos(2*pi*222*n/fs);
zeros(1,PointNum);
sampletab1 = sampletab;
index = 0;
for i = 1:PointNum
   index = bitreverse(PointBitNum,i - 1);
   sampletab(i) = sampletab1(index + 1);
end
REX = sampletab;
IMX = zeros(1,PointNum);
i = 0; 
j = 0; 
k = 0;
stages = log2(PointNum);
for i = 0 : stages - 1
   lenNum = 0; 
   for j = 0 : 2^(stages - (i + 1)) - 1
       for k = 0 : 2^i - 1
           R1 = REX(lenNum + 2^i + 1) * cos(2*pi*k*2^(stages - (i + 1))/PointNum); 
           R2 = IMX(lenNum + 2^i + 1) * sin(2*pi*k*2^(stages - (i + 1))/PointNum);
           T1 = REX(lenNum + 2^i + 1) * sin(2*pi*k*2^(stages - (i + 1))/PointNum);
           T2 = IMX(lenNum + 2^i + 1) * cos(2*pi*k*2^(stages - (i + 1))/PointNum);
           REX(lenNum + 2^i + 1) = REX(lenNum + 1) - R1 - R2;
           IMX(lenNum + 2^i + 1) = IMX(lenNum + 1)  + T1 - T2;
           REX(lenNum + 1) = REX(lenNum + 1) + R1 + R2;
           IMX(lenNum + 1) = IMX(lenNum + 1) - T1 + T2 ; 
           lenNum = lenNum + 1;
           endNum = lenNum + 2^i;    
       end  
       lenNum = endNum;
   end
end
subplot(3,1,1);
fft(sampletab1, PointNum);
x1 = abs(fft(sampletab1, PointNum))*2/PointNum;
x1(1)=x1(1)/2;
plot(n(1:PointNum/2)*fs/PointNum, x1(1:PointNum/2));
grid on
subplot(3,1,2);
am = sqrt(abs(REX.*REX) + abs(IMX.*IMX))*2/PointNum;
am(1)=am(1)/2;
plot(n(1:PointNum/2)*fs/PointNum, am(1:PointNum/2));
grid on
subplot(3,1,3);
plot(n, sampletab);
grid on
二、声音处理部分
[y,fs]=audioread('test.mp3');
% sound(y,fs)     % 回放语音信号
y=y(:,1);
n=length(y) ; %选取变换的点数 
y_p=fft(y,n);     %对n点进行傅里叶变换到频域
f=fs*(0:n/2-1)/n;   % 对应点的频率
t=(1:length(y))/fs;   %采样时间
figure(1)
subplot(2,1,1);
plot(t,y);                   %语音信号的时域波形图
title('原始语音信号采样后时域波形');
xlabel('时间轴')
ylabel('幅值 A')
subplot(2,1,2)
plot(f,abs(y_p(1:n/2))*2/length(y_p));    %语音信号的频谱图
title('原始语音信号采样后频谱图');
xlabel('频率Hz');
ylabel('频率幅值');
%对音频信号产生噪声
 L=length(y) ;      %计算音频信号的长度
 noise=0.1*randn(L,1); %产生等长度的随机噪声信号(这里的噪声的大小取决于随机函数的幅度倍数）
 y_z=y+noise;       %将两个信号叠加成一个新的信号——加噪声处理   
  %sound(y_z,fs)
%对加噪后的语音信号进行分析
n=length(y);  %选取变换的点数 
y_zp=fft(y_z,n);     %对n点进行傅里叶变换到频域
f=fs*(0:n/2-1)/n;   % 对应点的频率
figure(2)
subplot(2,1,1);
plot(t,y_z);                   %加噪语音信号的时域波形图
title('加噪语音信号时域波形');
xlabel('时间轴')
ylabel('幅值 A')
subplot(2,1,2);
plot(f,abs(y_zp(1:n/2))*2/length(y_zp));    %加噪语音信号的频谱图
title('加噪语音信号频谱图');
xlabel('频率Hz');
ylabel('频率幅值');
fp=1500;fc=1700;As=100;Ap=1;
wc=2*pi*fc/fs; wp=2*pi*fp/fs;
wdel=wc-wp;
beta=0.112*(As-8.7);
N=ceil((As-8)/2.285/wdel);
wn= kaiser(N+1,beta);
ws=(wp+wc)/2/pi;
b=fir1(N,ws,wn)
figure(3);
freqz(b,1);         
x=fftfilt(b,y_z);
X=fft(x,n);
figure(4);
subplot(2,2,1);plot(f,abs(y_zp(1:n/2))*2/length(y_zp));
title('滤波前信号的频谱');
subplot(2,2,2);plot(f,abs(X(1:n/2))*2/length(X));
title('滤波后信号频谱');
subplot(2,2,3);plot(t,y_z);
title('滤波前信号的波形')
subplot(2,2,4);plot(t,x);
title('滤波后信号的波形')
%sound(x,fs)  %回放滤波后的音频