CT-ICP
欢迎访问我的博客首页。
CT-ICP
- 1. 引言
- 2. 相关工作
- 3. CT-ICP 里程计
-
- 3.1 里程计
- 3.2 局部地图与健壮性
- 4. 回环闭合与后端
- 5. 实验
-
- 5.1 数据集
-
- 5.1.1 驾驶场景
- 5.1.2 高频运动场景
- 5.2 里程计实验
- 5.3 回环闭合实验
- 6. 结论
- 7. 参考
1. 引言
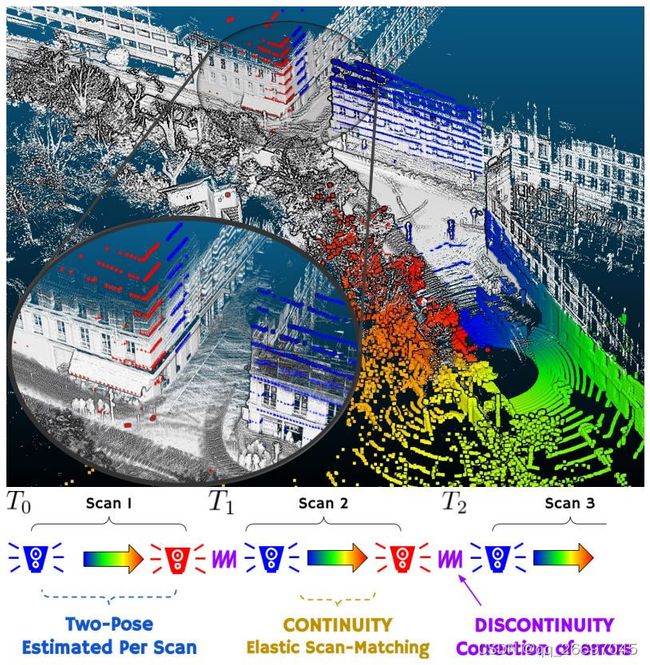
图 1 的上部是一幅图像,下部是一个示意图。上部的图像是地图点和一个扫描采集到的关键点。地图点是白色的,关键点是彩色的。如示意图中箭头的渐变色所示,蓝色代表时间戳最久的关键点,红色代表时间戳最新的关键点。
图 1 的下部是 CT-ICP 的位姿连续性理论示意图。第一次扫描从 T 0 T_0 T0 时刻开始到 T 1 T_1 T1 时刻结束,每次扫描的这两个开始位姿和结束位姿都是需要估计的。 第二次扫描从 T 1 T_1 T1 时刻开始到 T 2 T_2 T2 时刻结束。 T 1 T_1 T1 时刻和 T 2 T_2 T2 时刻之间的位姿是连续的,可以使用插值求出。第三次扫描从 T 2 T_2 T2 时刻开始。为了校正误差,CT-ICP 认为第二次扫描的结束位姿与第三次扫描的开始位姿不相等,即 T 2 T_2 T2 时刻的位姿是不连续的。
位姿连续性理论用于做运动补偿。假设 T 1 T_1 T1 时刻传感器的位姿是 p o s e 1 pose_1 pose1, T 2 T_2 T2 时刻传感器的位姿是 p o s e 2 pose_2 pose2。在匀速运动的情况下, T 1 T_1 T1 和 T 2 T_2 T2 之间的某个时刻 T 1. x T_{1.x} T1.x 的位姿就可以使用球面线性插值求得。
CT-ICP 的主要贡献有:
- 提出位姿连续性理论。
- 使用稀疏的体素结构存储基于稠密点云的局部地图,达到实时处理速度。
- 在 7 个高频运动驾驶场景数据集上实验,所有代码开源。
- 提出一个快速的回环检测方法,还实现了位姿图后端,构成一个完整的 SLAM。这些整合在 pyLiDAR-SLAM 中。pyLiDAR-SLAM 和 CT-ICP 是同一个人在 2021 年先后提出的,该作者把在 CT-ICP 中提出的快速回环检测方法整合到了他先前提出的 pyLiDAR-SLAM 中。
2. 相关工作
很多激光雷达里程计都基于 Point-to-Point ICP 方法或它的改进版 point-to-plane ICP 方法。根据当前扫描的参照物的不同,估计 RGB-D 传感器位姿的算法可以分为 frame-to-frame 和 frame-to-model。后者是 KinectFusion 提出的方法,估计结果更精确。与估计 RGB-D 传感器位姿的算法类似,估计激光雷达传感器的方法分为 scan-to-scan 和 scan-to-map。
参考文献 11 和 12 把一次扫描看成一幅深度图,地图由一系列面元(surfels)组成。参考文献 11 在注册(register)时,先把面元地图在 GPU 上投影得到渲染图像(rendered image),再把当前扫描与渲染图像对齐。参考文献 13 在深度图检测不同类别(边和平面)的关键点,再把检测到的点注册到一个体素栅格。但搜索每类关键点的近邻时,它使用单独的 kd 树。实时搜索使关键点地图非常稀疏。参考文献 14 把来自地面的关键点分割。参考文献 3 优化了注册过程,使得速度更快。参考文献 4 把关键点分成地面、外观、顶部、柱子、梁和顶点(ground, facade, roof, pillar, beam, and vertex)。参考文献 15 把地图看成稠密点云,参考文献 16 使用 TSDF 算法,参考文献 17 使用无限网格,这三种算法都不能实时进行。
为了解释扫描过程中的传感器运动,很多方法先使用匀速运动模型把当前扫描变换(distort)到前面的坐标系,然后这个变换在 ICP 迭代过程中保持不变。尽管该方法在大多数驾驶场景中表现不错,但它对突然的方向变化和快速的速度变化不健壮。
其它方法使用线性插值或 B 样条曲线(B-splines)定义一个带控制位姿的连续时间轨迹(a continuous-time trajectory with control poses)。参考文献 18 使用每个扫描的多个位姿定义轨迹。参考文献 19 使用每个扫描带 6 个位姿的连续时间轨迹,使用 B 样条曲线基准表示轨迹。但这些方法都不能实时。最近参考文献 5 和 6 提出了连续时间的轨迹,可以达到实时效果。参考文献 5 使用位姿的线性插值,在里程计中使用面元的稀疏地图,建图时使用稠密的 2 维磁盘面元。参考文献 6 在连续时间的轨迹在使用 B 样条曲线,使用多分辨率的面元地图实现实时速度。这些方法使轨迹平滑,但没有考虑传感器的摇晃(尤其是地面不平时)和高频运动(涉及到控制点频率)。
相反,CT-ICP 定义的轨迹在扫描内连续,在扫描间间断。在一个扫描过程中,轨迹可以使用开始位姿和结束位姿表示。和参考文献 5 和 6 不同的是,CT-ICP 的最终轨迹是不连续的,因为一次扫描的开始位姿不等于上一次扫描的结束位姿。这种方法考虑到插值不适用于不规则运动。
激光雷达里程计在开发环境中依然有累积误差,这会导致轨迹偏移。回环闭合可以全局矫正轨迹,但回环检测仍然是一个开放性的问题。现在大多数解决方法都主要依赖配准法( registration methods)直接闭合回环。这样只能处理小规模轨迹和较小偏移。很多位置识别方法都在每一个扫描中识别位置,这对环境变化很敏感,更适合驾驶场景。参考文献 4 在基于 ICP 的改进前使用一个全局配准处理,但每次对齐的代价都很大,所以不能检测更多回环。最近和多基于深度学习的方法被提出,但由于训练样本,这些方法不适用于新环境。CT-ICP 的回环闭合算法作用于投影在一个高程图像上的汇聚点云(aggregated point clouds)。该方法需要传感器的运动接近 2 维,且需要估计重力矢量。该方法可以用于任何满足这些条件的激光雷达里程计。参考文献 22 和该方法相似,它构造高程图像但在每次的扫描中检测回环,而 CT-ICP 在局部地图中检测回环。因此 CT-ICP 不需要检查每次扫描是否与之前的位置一样。这在在线 SLAM 场景中更高效。
3. CT-ICP 里程计
CT-ICP 里程计可以使用两个位姿表示,一个是起始位姿 Ω b n = ( R b n , t b n ) \Omega_b^n = (R_b^n, t_b^n) Ωbn=(Rbn,tbn),另一个是结束位姿 Ω e n = ( R e n , t e n ) \Omega_e^n = (R_e^n, t_e^n) Ωen=(Ren,ten)。其中 R 和 t 分别表示旋转和平移,b 和 e 分别表示起始和结束。为了简便,下面用 n 表示传感器当前的位姿。
3.1 里程计
为了获取更大视野,通常把激光雷达在一段运动范围内的扫描称为一次扫描。使用两个位姿可以把 CT-ICP 的一次扫描参数化:一个位姿 Ω b n = ( R b n , t b n ) \Omega_b^n = (R_b^n, t_b^n) Ωbn=(Rbn,tbn) 代表本次扫描开始时的位姿,另一个位姿 Ω e n = ( R e n , t e n ) \Omega_e^n = (R_e^n, t_e^n) Ωen=(Ren,ten) 代表本次扫描结束时的位姿。其中 R 和 t 分别代表旋转和平移,b 和 e 分别代表开始和结束。
每次扫描开始时刻 t b t_b tb 和结束时刻 t e t_e te 中间的某个时刻 t t t 对应的位姿,可以用 t b t_b tb 和 t e t_e te 时刻的位姿插值(比如球面线性插值)表示。位姿变换的作用是把一个点从雷达传感器的坐标系 L ( t ) L(t) L(t) 变换到世界坐标系 W = L ( 0 ) W=L(0) W=L(0)。 L ( 0 ) L(0) L(0) 就是第一次扫描时雷达传感器的坐标系。
假设第 n 次扫描的开始位姿是 Ω b n \Omega_b^n Ωbn,上一次扫描的结束位姿是 Ω e n − 1 \Omega_e^{n-1} Ωen−1。 连续时间轨迹的方法把这两个位姿看成是相等的。真实情况是,传感器运动频率越高,这两个位姿的差异就越大。因此,我们在优化时添加一个临近约束(proximity constraint),只让这两个位姿尽可能接近,而不默认它们相等。
对每一次新扫描 S n \mathbb{S}^n Sn,我们先使用简单的网格抽样算法提取一些样本点,并用 I n \mathbb{I}^n In 编号,即 p i ∈ S n ∣ i ∈ I n {p_i \in S^n | i \in I^n} pi∈Sn∣i∈In。然后把这些点加入(register)局部地图。该地图是个稠密的点云地图 M n = q i W M^n={q_i^W} Mn=qiW,由前面的 n-1 次扫描得到, 存储在一个稀疏体素(voxel)栅格中。详细结构见《局部地图和健壮性方案》。CT-ICP 的扫描匹配算法估计两个最优位姿 Ω b ∗ \Omega_b^* Ωb∗ 和 Ω e ∗ \Omega_e^* Ωe∗,然后把点转换到世界坐标系进而加入局部地图。
这两个最优位姿在下面公式中用黑体公式 X = ( Ω b , Ω e ) ∈ S E E ( 3 ) 2 X = (\Omega_b, \Omega_e) \in SEE(3)^2 X=(Ωb,Ωe)∈SEE(3)2 表示。
arg min X ∈ S E ( 3 ) 2 F I C P ( X ) + β l C l o c ( X ) + β v C v e l ( X ) (1) { \underset { {\bf X} \in SE(3)^2 } {\operatorname {arg \, min}} }\, F_{ICP}({\bf X}) + \beta_lC_{loc}({\bf X}) + \beta_vC_{vel}({\bf X}) \tag{1} X∈SE(3)2argminFICP(X)+βlCloc(X)+βvCvel(X)(1)
其中 F I C P F_{ICP} FICP 是 scan-to-map continuous-time 的 ICP:
F I C P ( X ) = 1 ∣ I n ∣ ∑ i ∈ I n ρ ( r i 2 [ X ] ) (2) F_{ICP}({\bf X}) = \frac{1}{| \Bbb I^n |} \sum_{i \in \Bbb I^n} \rho (r_i^2 [{\bf X}]) \tag{2} FICP(X)=∣In∣1i∈In∑ρ(ri2[X])(2)
对每一个 i ∈ I n i \in \Bbb I^n i∈In,
r i [ X ] = a i ( p i W [ X ] − q i W ) ⋅ n i p i W [ X ] = R α i [ X ] ∗ p i L + t α i [ X ] R α i [ X ] = s l e r p ( R b , R e , α i ) t α i [ X ] = ( 1 − α i ) t b + α i t e (3-6) \begin{aligned} r_i[{\bf X}] &= a_i (p_i^W[{\bf X}] - q_i^W) \cdot n_i \\ p_i^W[{\bf X}] &= R^{\alpha_i} [{\bf X}] * p_i^L + t^{\alpha_i} [{\bf X}] \\ R^{\alpha_i} [{\bf X}] &= slerp({\bf R_b, R_e}, \alpha_i) \\ t^{\alpha_i} [{\bf X}] &= (1 - \alpha_i) {\bf t_b} + \alpha_i {\bf t_e} \end{aligned} \tag{3-6} ri[X]piW[X]Rαi[X]tαi[X]=ai(piW[X]−qiW)⋅ni=Rαi[X]∗piL+tαi[X]=slerp(Rb,Re,αi)=(1−αi)tb+αite(3-6)
ρ ( s ) \rho(s) ρ(s) 是一个健壮的损失函数,用于降低异常值的影响。 r i r_i ri 是样本点 p i W p_i^W piW 与局部地图中距离它最近的点 p n e a r e s t p_{nearest} pnearest 的 point-to-plane 距离(优化的目的是让这个距离尽可能小)。 p i W [ X ] p_i^W[{\bf X}] piW[X] 是 p i p_i pi 在世界坐标系中的坐标。 n i n_i ni 是 p i W p_i^W piW 邻域的法线。传感器在平面上运动,这个法线垂直于运动平面,与 z 轴平行。 p i L p_i^L piL 是传感器测量到的,在传感器坐标系中的坐标。 Ω α i [ X ] = ( R α i , t α i ) ∈ S E ( 3 ) {\bf \Omega ^{\alpha_i}[X] = (R^{\alpha_i}, t^{\alpha_i})} \in SE(3) Ωαi[X]=(Rαi,tαi)∈SE(3) 是在时刻 τ i \tau_i τi,从传感器坐标系中的坐标 L ( τ i ) L(\tau_i) L(τi) 到世界坐标系的坐标变换。它通过 Ω b \bf \Omega_b Ωb 和 Ω e \bf \Omega_e Ωe 插值而来: α i = ( τ i − τ b ) / ( τ e − τ b ) \alpha_i = (\tau_i - \tau_b) / (\tau_e - \tau_b) αi=(τi−τb)/(τe−τb)。旋转部分使用标准的球面线性插值。
我们还像参考文献 15 那样,使用权重鼓励(favor)平面邻域: a i = a 2 D = ( σ 2 − σ 3 ) / σ 1 a_i = a_{2D} = (\sigma_2 - \sigma_3) / \sigma_1 ai=a2D=(σ2−σ3)/σ1,用于使 p i W p_i^W piW 的近邻平面化。和参考文献 15 不同的是,我们使用局部地图中的稠密点云而不是当前扫描,计算法线 n i n_i ni 和平面权重 a i a_i ai,这样可以获取更多近邻(局部地图中的点多于当前扫描到的点)。每次 ICP 迭代时,对每个样本点 p i p_i pi 都会计算这个平面权重。
在公式 (1) 中,我们还添加了另外两个约束条件,用于约束传感器的空间位置 t t t:位置一致性约束 C l o c C_{loc} Cloc 和匀速约束 C v e l C_{vel} Cvel。前者假设传感器扫描是不间断的,使第 n 次扫描的开始位置接近第 n-1 次扫描的结束位置。后者假设传感器是高速运动的,使第 n 次扫描过程中的路程接近第 n-1 次扫描。这两个约束的系数都使用 0.001,以使 CT-ICT 对运动模型更具弹性。
C l o c ( t b ) = ∣ ∣ t b − t e n − 1 ∣ ∣ 2 C v e l ( t b , t e ) = ∣ ∣ ( t e − t b ) − ( t e n − 1 − t b n − 1 ) ∣ ∣ 2 (7-8) \begin{aligned} C_{loc} ({\bf t_b}) &= || {\bf t_b} - t_e^{n-1} ||^2 \\ C_{vel} ({\bf t_b, t_e}) &= || {\bf (t_e - t_b)} - (t_e^{n-1} - t_b^{n-1}) ||^2 \end{aligned} \tag{7-8} Cloc(tb)Cvel(tb,te)=∣∣tb−ten−1∣∣2=∣∣(te−tb)−(ten−1−tbn−1)∣∣2(7-8)
CT-ICP 使用两个求解器最小化公式 1。
- 使用 CERES 作非线性最小二乘。这让损失函数 ρ ( s ) \rho(s) ρ(s) 有多种选择,比如 huber、cauchy 和 truncated。
这让我们的求解更通用、更健壮。但它们都需要多线程实时求解。 - 使用高斯牛顿算法作线性近似,实现一个缩减版的 ρ ( s ) \rho(s) ρ(s)。这个求解只需要一个线程。手工计算的雅可比不允许修改约束。我们的所有实验都使用的是把这个求解器。
3.2 局部地图与健壮性
我们使用过往的扫描作为局部地图。体素用于存储世界坐标系中的点,为了快速访问临近体素,体素使用稀疏的数据结构实现,而不是使用 kd 树。
所以与kd树相比,其访问时间复杂度是线性的,而不是对数。对于驾驶场景来说,高频运动场景下,局部地图的体素尺寸是1米和0.8米。
体素的尺寸就是地图的栅格大小,它决定邻近搜索半径和局部地图的详细程度。每个体素存储的点达到 20 个,为了避免冗余,任意两个点的距离都不小于10厘米。为了构造点 p i W p_i^W piW 的近邻(用于计算法向量 n i n_i ni 和平面权重 a i a_i ai),我们在地图中离该点最近的 27 个(边长为 3 的立方体)体素中找出 k = 20 k = 20 k=20 个最近点。处理完当前扫描后,点被加入局部地图。体素被占满时,其中的点将被删除(为什么)。我们的局部地图不像 pyLiDAR 的 F2M 不一样,局部地图不会使用滑动窗口丢弃点云。
如果向地图中添加错误的数据,或者方向变化较快,使用滑动窗口丢弃点云的地图很容易受影响。对于方向变化快的数据,我们提出一个健壮性的方案:检测困难情况(快速的方向变化)和失败的注册(registration)(位置不一致或者大量新关键点落入空体素),使用更保守的参数重新注册;如果方向变化大于5度,我们就不会把新的扫描结果插入地图,否则很可能偏离方向。健壮性的提高会增加一定的时间复杂度。
4. 回环闭合与后端
CT-ICP 的回环闭合算法在内存中维持一个窗口,窗口内是里程计最近添加(register)进来的扫描。当窗口大小等于 N m a p N_{map} Nmap 个扫描时,点就会被加入位于窗口中心位置的那个扫描的点云中。解释:假如窗口大小是 9,如果窗口内有 9 个扫描,就把窗口内的点加入第 5 个扫描的点云中。这是因为一般情况下,第 5 个扫描与其它 8 个扫描的重合最多。
地图的每个点都会被插入一个 2 维的高程栅格(elevation grid),让每个像素的点保持最大高度(elevation)。在这个 2 维栅格内,以点的最小 z 坐标 z m i n z_{min} zmin 和最大 z 坐标 z m a x z_{max} zmax 作为 z 轴的范围,得到高程图像(elevation image)。然后提取 2 维旋转不变特征,与高程栅格一块保存在内存中。除了最后 N o v e r l a p N_{overlap} Noverlap 个扫描,其它都被移出窗口。
每一个新创建的高程图像(包含 N m a p − N o v e r l a p N_{map} - N_{overlap} Nmap−Noverlap 个扫描),都会与内存中的高程图像匹配。使用 2 维刚体变换和 RANSAC 算法,把新创建的高程图像变换到与内存中保存的高程图像一致。如果能匹配,就对高程栅格的点云,使用 ICP 改善算法(Open3D 的 ICP 算法)提高 2 维刚体变换,得到一个精确的 6 自由度闭环约束。为了减少候选数量,使用阈值 n c a n d i d a t e s = 10 n_{candidates} = 10 ncandidates=10 筛选与当前高程栅格最近的 10 个高程栅格。这个阈值与误差有关,阈值过小导致闭环的漏检。
CT-ICP 的后端使用 g2o 实现标准的位姿图。位姿图定期添加新位姿,但只有检测到闭环时,才对整个轨迹作全局优化。
CT-ICP 的算法需要传感器在平面上运动(上下运动幅度小),还需要外参标定以对齐 z 坐标与实际平面。这限制了传感器和运动。如果重力矢量或者局部平面已知,高程图像就能正确地投影,这个限制也就没有了。但我们在第 Ⅴ 部分说了,在室外场景中,使用向上的传感器,使我们的闭环检测成功检测到一些闭环。
5. 实验
CT-ICP 在多个数据集上验证其算法效率高适用性强。CT-ICP 只需要每个点的三维坐标和时间戳。
5.1 数据集
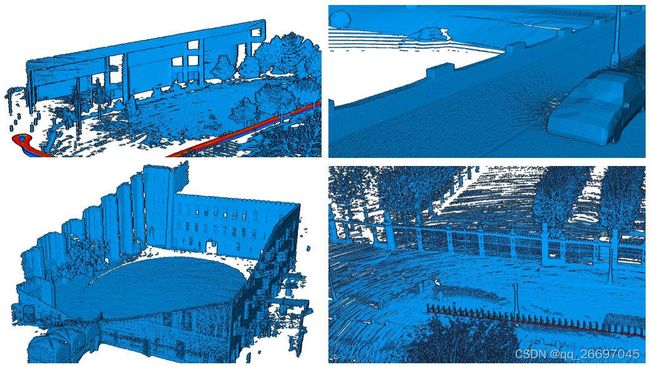
图 2 是 CT-ICP 使用不同数据集得到的点云地图。左上是 NCLT 数据集,右上是 KITTI-CARLA 数据集,左下是 Newer College 数据集,右下是 ParisLuco 数据集。
5.1.1 驾驶场景
KITTI 数据集使用固定在轿车上的威力登 HDL64 激光雷达获取了包含 11 个场景的数据集,以及使用 GPS 和 IMU 获取的实际位姿。它的里程计基准(benchmark)进行(propose)运动校正扫描,即使用相机变换(distort)扫描,我们称之为 KITTI-corrected。大多数里程计方法都与 KITTI 的运动矫正版结果比较,但这就无法使用原生雷达数据测试它们的结果。除了 sequence 03,KITTI 的其它里程计 sequence 都包含未矫正的原生扫描数据,我们称之为 KITTI-raw。
KITTI-360 的采集设置和上面的 KITTI 相同,它包含 8 个 sequences。虽然 KITTI-360 的场景与 KITTI 相同,但它的 sequences 更长,包含 3000 到 15000 个扫描。这些扫描没有被校正,其时间戳的估计如前所述。和参考文献 15 一样,使用 KITTI-corrected、KITTI-raw 和 KITTI-360 时,CT-ICP 使用 0.205 度的内在角(intrinsic angle)校正所有扫描。
KITTI-CARLA 是使用 CARLA 模拟器生成的类似 KITTI 的数据集。它包含 7 个 sequences 共 5000 个扫描。每个扫描都包含精确的实际值和时间戳。
ParisLuco 是一个包含 4 千米场景 12751 个扫描的 sequences。其场景是巴黎中心,使用垂直方向的威力登 HDL32 传感器采集而来。
CT-ICP 使用 GPS/IMU 作后处理,从而得到相应的标注信息(只有变换)。
5.1.2 高频运动场景
匀速运动模型是指汽车的加速度相对慢于传感器的采集速度。传感器方向快速变化的场景具有挑战性,NCLT 就是这种数据集。它包含 27 和长 sequences,每个 sequences 包含超过 20 000 个扫描。它是使用两轮电动平衡车和威力登 HDL32 传感器,在密歇根大学内获取的数据。这个数据集包含突然的旋转,对基于经典 ICP 算法的里程计来说具有很大挑战。
NCD 即 Newer College Dataset,包含两个 sequences,约 15000 到 26000 个扫描。它是把 ouster 64通道传感器安装在棍子上,然后手持着在牛津大学校园获取的数据集。
5.2 里程计实验
CT-ICP 使用的评价指标是 KITTI 的相对变换误差 Relative Translation Error,简称 RTE,它是轨迹在 100 米到 800 米内的偏差平均值。AVG 指标用于评价多个 sequence 的得分,和 RTE 求平均值不同,它求的是所有 sequence 上的偏差。
CT-ICP 与另外三个里程计 MULLS、IMLS-SLAM 和 pyLIDAR-SLAM F2M 比较。前两个里程计专门处理驾驶场景的数据集,第三个里程计可以处理高频运动数据集 NCD 和 NCLT。
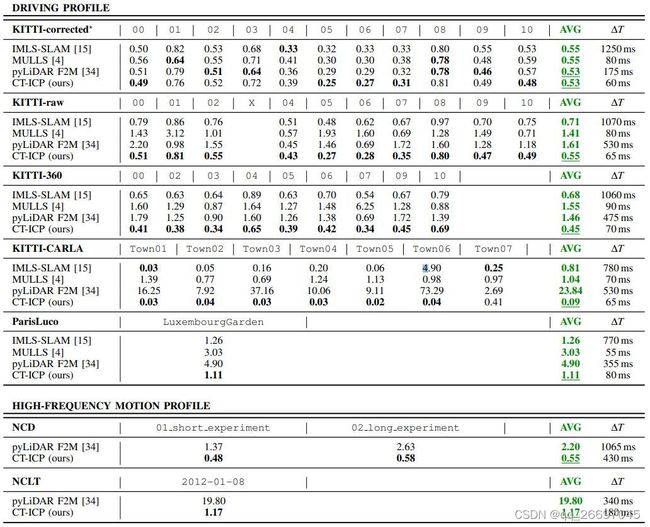
表 1 是在 5 个驾驶场景数据集和 2 个高频运动场景数据集上的相对变换误差 RTE。AVG 是所有 sequences 上 RTE 的平均值, Δ T \Delta T ΔT 是每个扫描的平均耗时。KITTI-corrected 是唯一一个被校正过的数据集,其它数据集的点云都是原始未校正的。
从表 1 可以看出,所有里程计方法在经过运动校正的 KITTI-corrected 数据集上表现接近。处理未校正的数据集 KITTI-raw 和 KITTI-360 时,其它方法的表现明显变差,而 CT-ICP 在未校正的数据集上的表现接近其在校正过的数据集上的表现。在校正过的数据集上,CT-ICP 的弹性策略(elastic formulation)不起作用,这表明了 CT-ICP 的地图和 scan-to-map 算法的有效性。在 KITTI 的在线评测上,CT-ICP 以 0.59% 的 RTE 排名第一。
表 1 的 KITTI-corrected 数据集上,CT-ICP 的结果与 MULLS 不同,这是因为 CT-ICP 把一套参数用于所有 sequence,而 MULLS 针对城市、高速公路和村庄场景,使用三套不同的参数。
KITTI-CARLA 数据集的速度变化比 KITTI 快。在该数据集上,CT-ICP 的表现比其它方法都好:CT-ICP 的 RTE 仅为 0.09%,其它方法的最好结果是 0.81%。这证明 CT-ICP 的弹性策略和扫描间位姿不连续策略可以有效弥补位姿误差。
不同于 KITTI 的 64 线激光雷达,ParisLuco 数据集的雷达是 32 线的。由于获取于市中心,ParisLuco 是低惯性的(low inertia)。在该数据集上,CT-ICP 能超过使用稠密地图的 IMLS-SLAM。
NCD 和 NCLT 数据集使用棍子和平衡车采集,所以不稳定。而且它们的每个 sequence 包含更多扫描,环境也多样(植被、道路、室内、室外),因此更具挑战性。此外这两个数据集还有很多边界情况,比如快速地从室内转移到室外、急转弯、运动的高频间断引起的扫描大变形。一般的雷达里程计很难处理这些情况。表 1 表明 CT-ICP 在 NCD 数据集上表现优秀。在 NCLT 数据集上的实验也证明了 CT-ICP 的健壮性,因为 CT-ICP 在处理边界情况时,RTE 比 pyLiDAR F2M 还低。
为了专门验证 CT-ICP 的主要贡献,即其弹性策略,只使用匀速运动模型扭曲(distort)扫描,以测试里程计。在 KITTI-raw 上,RTE 从 0.55% 增加到 0.79%,在 KITTI-360 上,RTE 从 0.45% 增加到 0.60%。
5.3 回环闭合实验
在所有数据集上,CT-ICP 使用的回环闭合模型都是 CT-ICP 加回环闭合,其中 N m a p = 100 N_{map} = 100 Nmap=100, N o v e r l a p = 30 N_{overlap} = 30 Noverlap=30。 z m i n z_{min} zmin 略低于标注值(使用传感器获取一个近似的外部标定), z m a x z_{max} zmax 比 z m i n z_{min} zmin 大 10 米。对于 NCLT,使用刚体变换把向下的 z 轴变换成向上。每个高程珊格的计算时间加上与前一个高程珊格的匹配时间,平均需要 1.1 秒。位姿图优化平均需要 1.2 秒。当前的回环闭合由主线程负责,利用多线程可以实现实时。
图 3 是 CT-ICP 里程计估计出的轨迹和回环闭合校正效果。第 1 幅图是在 KITTI-raw 数据集 sequence 00 的 4541 个扫描上的实验结果,第 2 幅图是在 KITTI-360 数据集 sequence 06 的 9698 个扫描上的实验结果,第 3 幅图是在 KITTI-CARLA 数据集 Town 01 的 5000 个扫描上的实验结果,第 4 幅图是在 NCD 数据集 01_short_experiment 的 15301 个扫描上的实验结果,第 5 幅图是在 NCLT 数据集 2012-01-08 的 42764 个扫描上的实验结果。
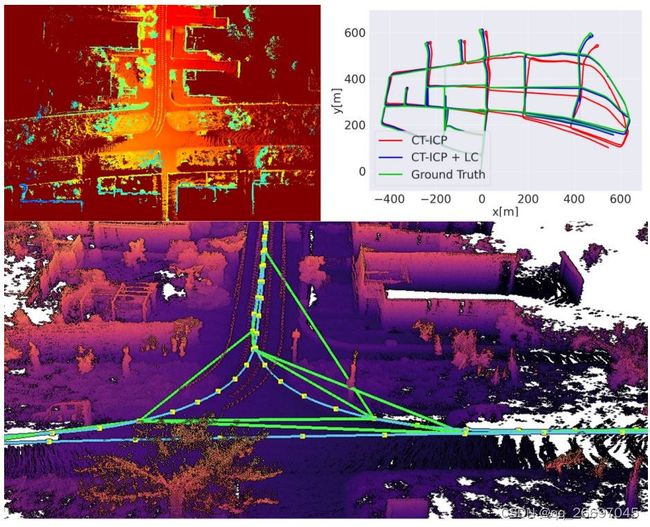
图 4 是在 KITTI-360 数据集 sequence 00 的 11501 个扫描上,回环闭合的量化结果。左上部是投影局部地图得到的一个高程图像,右上部是 CT-ICP 里程计轨迹和回环闭合(CT-ICP 加回环闭合)校正效果,下部是在左上图所示的局部地图中发现的多个闭环约束(使用绿色表示)。
回环闭合的量化结果如图 3 和图 4。RTE 不适合在回环闭合中作为评价指标,使用标准的绝对轨迹误差 ATE 验证轨迹的全局优化效果。为了排除最初位姿的方向误差,计算 ATE 前先估计标注值与估计的轨迹间的最佳刚体变换。
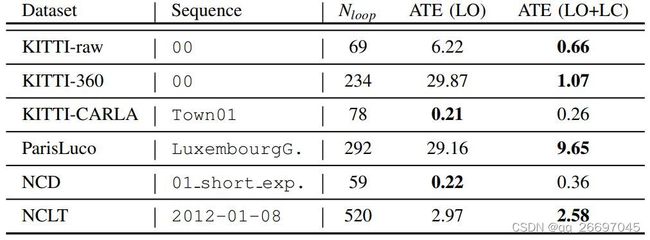
表 2 是回环闭合在每个数据集的一个 sequence 上的实验结果。ATE 是固定了估计轨迹于实际轨迹间的刚体变换后的平均绝对轨迹误差,单位是米。 N l o o p N_{loop} Nloop 是检测到的回环数量。LO 代表激光雷达里程计,LC 代表回环闭合。
表 2 是在各数据集的其中一个 sequence 上的实验结果。首先,记录 CT-ICP 在 KITTI-raw、KITTI-360 和 ParisLuco 数据集上,回环闭合的最好结果。KITTI-360 的 ATE 在闭合前后变化很大,这是因为它的 sequence 最长。KITTI-CARLA 的 ATE 在回环闭合前后变化不大,这是因为该数据集包含的路径几何形状简单,也就是说平面大且平整。所以扫描匹配的挑战性主要受传感器采集数据时的运动情况影响。CT-ICP 的对齐效果接近完美,达到了 ATE 为 21 厘米的精度,如图 3 所示,其估计的轨迹与标注值几乎重合。
最后,在每个 sequence 上检测多个回环。回环的数量取决于高程栅格的构造频率,也就是和重叠大小 N o v e r l a p N_{overlap} Noverlap 以及地图大小 N m a p N_{map} Nmap 有关。每到交叉路口,就计算回环约束,如图 4。重叠大小 N o v e r l a p N_{overlap} Noverlap 越大,越能检测出更多回环(包括连续的局部地图间的约束)。
6. 结论
CT-ICP 提出了一个新的实时里程计。在包含驾驶场景和高频运动场景的 7 个数据集上,进行了多方面的评比,CT-ICP 都超过现有方法。
CT-ICP 的核心是连续的扫描匹配算法,它在优化时,弹性地变换(distort)一个新扫描,以弥补采集数据时的运动。
CT-ICP 提供所有代码和数据集以供验证所有实验结果。未来,CT-ICP 会着重于后端,进一步延伸扫描外的连续策略,充分利用提出的回环闭合算法。
7. 参考
- 论文,Arxiv。
- 源码,Github
- 译文,知乎专栏。
- 体素 voxel,知乎专栏。
- 平面邻域 1,arxiv,2018。
- 平面邻域 2,semantic scholar,2011。
- F-LOAM 畸变补偿,Arxiv,2021。