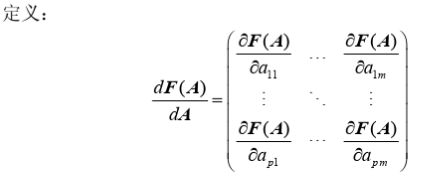
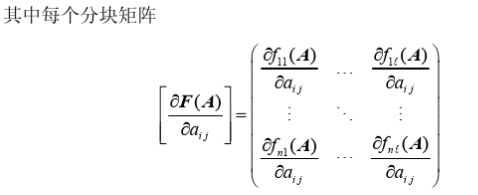
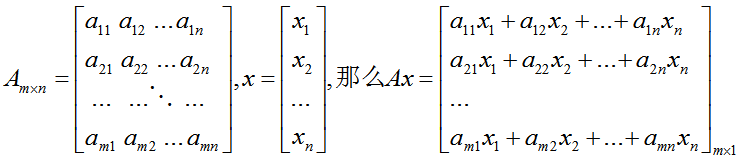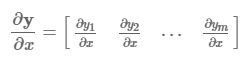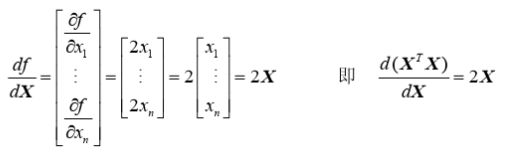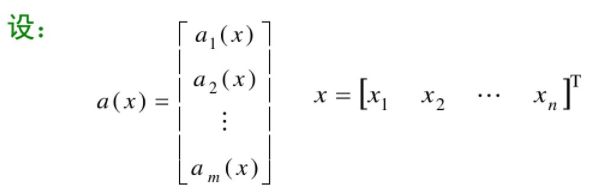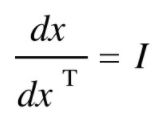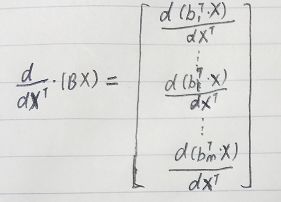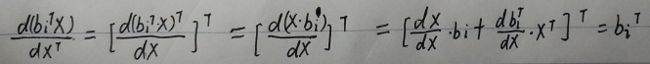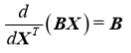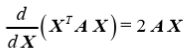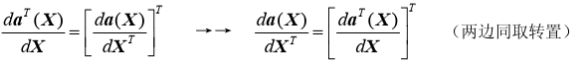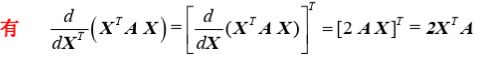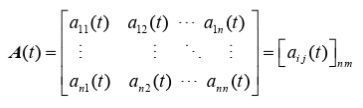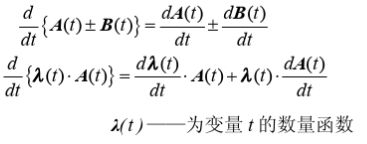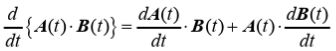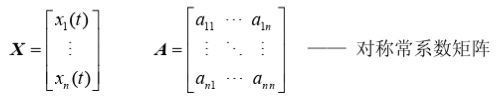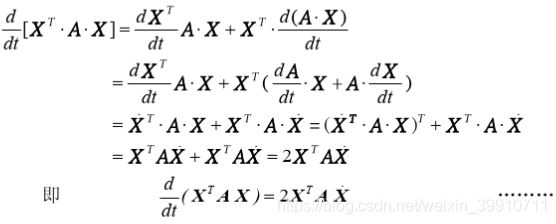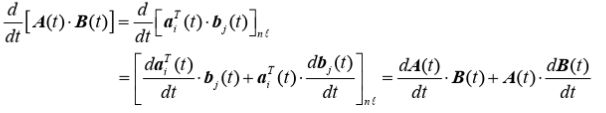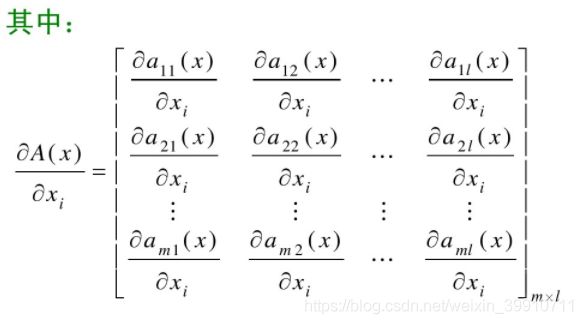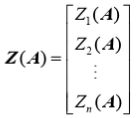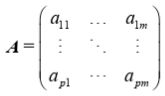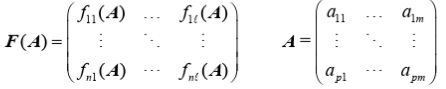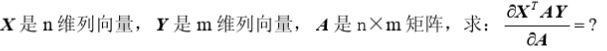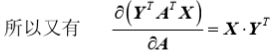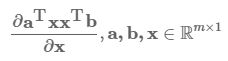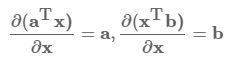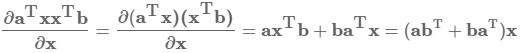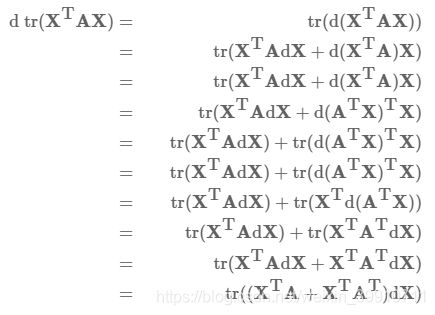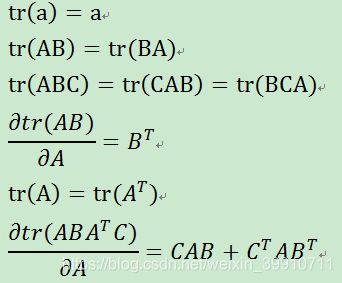矩阵的求导

目录

1 布局(Layout)

1.1 矩阵向量求导引入

1.2 矩阵向量求导定义

1.3 矩阵向量求导布局

1.4 分母布局的另一种求解方法

1.5 总结

2 基本的求导规则

2.1 向量对标量求导（相对于数量变量的微分，即自变量是数量变量）

2.1.1 定义

2.1.2 运算法则

2.2 标量 y 对向量 x 求导（数量函数相对于向量的微分）

2.2.1 定义

2.2.2 运算法则

2.2.3 示例

2.3 向量对向量求导

2.3.1 定义

2.3.2 运算法则

2.3.3 示例

2.4 标量对矩阵求导

2.4.1 定义

2.4.2 示例

2.5 矩阵对标量求导（分子布局）

2.5.1 定义

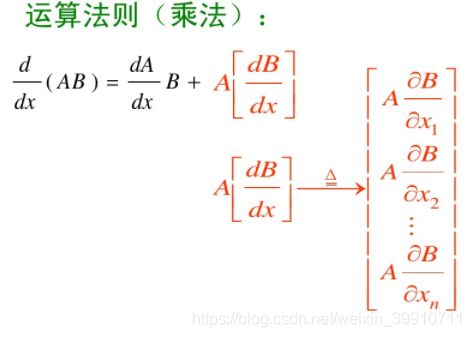
2.5.2  运算法则：

2.5.3 示例

2.6 矩阵函数相对于向量的微分

2.6.1 定义

2.6.2 运算法则

2.7 向量相对于矩阵函数的微分（分母布局）

2.8 矩阵函数相对于矩阵函数的微分

2.8.1 定义

2.8.2 示例

2.9 复合函数的微分

3 维度分析（针对前三类问题）

3.1 例一

3.2 例二

4 矩阵的迹求导（微分形式）（标量对矩阵求导）

5 推导公式

5.1 例一

5.2 例二

5.3 例三

6 应用到线性回归

6.1 通过链式法则

6.2 将式子拆开然后每个项求导

7 “前导不变后导转置”向量求导法则

8 矩阵导数的基本运算规律

8.1 转置

8.2 矩阵的基本运算

---

1 布局(Layout)

1.1 矩阵向量求导引入

        在高等数学里面，我们已经学过了标量对标量的求导，比如标量 y 对标量 x 的求导，可以表示为。

　　有些时候，我们会有一组标量来对一个标量 x 的求导,那么我们会得到一组标量求导的结果：

                 

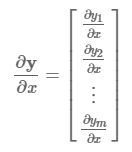
　　如果我们把这组标量写成向量的形式，即得到维度为m的一个向量 y 对一个标量 x 的求导，那么结果也是一个m维的向量：

　　可见，所谓向量对标量的求导，其实就是向量里的每个分量分别对标量求导，最后把求导的结果排列在一起，按一个向量表示而已。类似的结论也存在于标量对向量的求导，向量对向量的求导，向量对矩阵的求导，矩阵对向量的求导，以及矩阵对矩阵的求导等。

　　总而言之，所谓的向量矩阵求导本质上就是多元函数求导，仅仅是把把函数的自变量，因变量以及标量求导的结果排列成了向量矩阵的形式，方便表达与计算，更加简洁而已。

　　为了便于描述，后面如果没有指明，则第一章求导的自变量用 x（不加粗） 表示标量，x（加粗）表示n维向量，X 表示 m×n 维度的矩阵，求导的因变量用 y（不加粗） 表示标量，y （加粗）表示m维向量，Y表示 p×q 维度的矩阵。

1.2 矩阵向量求导定义

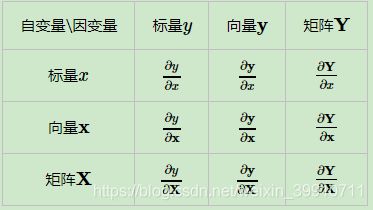
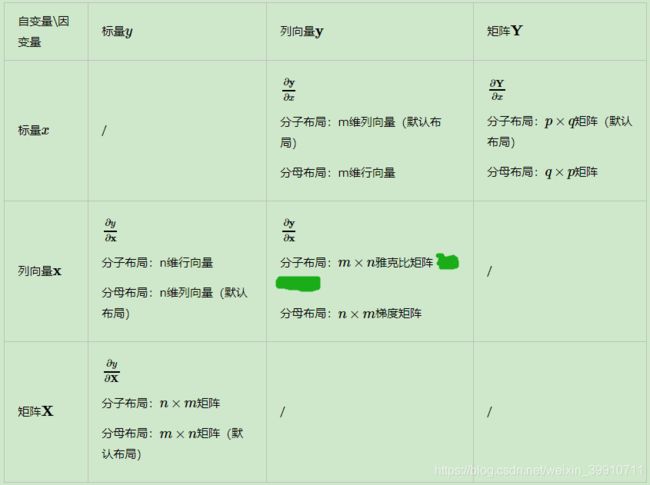
        根据求导的自变量和因变量是标量，向量还是矩阵，我们有9种可能的矩阵求导定义，如下：

           

        这9种里面，标量对标量的求导高数里面就有，不需要我们单独讨论。在剩下的8种情况里面，我们先讨论上图中标量对向量或矩阵求导，向量或矩阵对标量求导，以及向量对向量求导这5种情况。另外三种向量对矩阵的求导，矩阵对向量的求导，以及矩阵对矩阵的求导我们在后面再讲。

　　1.1节中讲到的例子，维度为m的一个向量y对一个标量x 的求导，那么结果也是一个m维的向量：。这是我们表格里面向量对标量求导的情况。这里有一个问题没有讲到，就是这个m维的求导结果排列成的m维向量到底应该是列向量还是行向量？

        这个问题的答案是：行向量或者列向量皆可！毕竟我们求导的本质只是把标量求导的结果排列起来，至于是按行排列还是按列排列都是可以的。但是这样也有问题，在我们机器学习算法法优化过程中，如果行向量或者列向量随便写，那么结果就不唯一，乱套了。

　　为了解决这个问题，我们引入求导布局的概念。

1.3 矩阵向量求导布局

        矩阵求导，想必许多领域能见到。不同的文献中，同样的式子求导的结果有时候会不一样，仔细观察会发现刚好相差一个转置，于是我们得先说说求导的两个派别（布局）。

      矩阵求导有两种布局，分子布局(numerator layout)和分母布局(denominator layout)。如下所示：

（1）向量和标量

• 对于分子布局来说，我们求导结果的维度以分子为主，比如对于我们上面向量对标量求导的例子，结果的维度和分子的维度是一致的。也就是说，如果向量y是一个m维的列向量，那么求导结果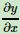也是一个m维列向量。如果向量y是一个m维行向量，那么求导结果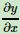也是一个m维行向量。
• 对于分母布局来说，我们求导结果的维度以分母为主，比如对于我们上面向量对标量求导的例子，如果向量y是一个m维的列向量，那么求导结果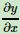是一个m维行向量。如果向量y是一个m维的行向量，那么求导结果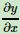是一个m维的列向量。

       可见，对于分子布局和分母布局的结果来说，两者相差一个转置。

（2）矩阵和向量

       标量y 对矩阵X（m×n）求导：

•     如果是分子布局，则求导结果的维度为 n×m 。
•     如果按分母布局，则求导结果的维度和矩阵X的维度 m×n 是一致的。

        这样，对于标量对向量或者矩阵求导，向量或者矩阵对标量求导这4种情况，对应的分子布局和分母布局的排列方式已经确定了。

（3）向量和向量

        稍微麻烦点的是向量对向量的求导，本文只讨论列向量对列向量的求导，其他的行向量求导只是差一个转置而已。比如m维列向量y 对 n维列向量x 求导。对于这2个向量求导，那么一共有 mn个标量对标量的求导。求导的结果一般是排列为一个矩阵。

       例如，假设 y 为 m 维列向量，x 为 n 维列向量。 ，如果采用的是分子布局，则是 m×n 矩阵，而如果采用的是分母布局，则是 n×m 矩阵。

（1）分子布局，矩阵的第一个维度以分子为准，即结果是一个 m×n 的矩阵：

          

        上边这个按分子布局的向量对向量求导的结果矩阵，我们一般叫做雅克比 (Jacobian)矩阵。有的资料上会使用来定义雅克比矩阵，意义是一样的。

 （2）分母布局，求导的结果矩阵的第一维度会以分母为准，即结果是一个 n×m 的矩阵：

         

        上边这个按分母布局的向量对向量求导的结果矩阵，我们一般叫做梯度矩阵。有的资料上会使用来定义梯度矩阵，意义是一样的。

        这两种布局间的关系是

        有了布局的概念，我们对于上面5种求导类型，可以各选择一种布局来求导。但是对于某一种求导类型，不能同时使用分子布局和分母布局求导。

　 　但是在机器学习算法原理的资料推导里，我们并没有看到说正在使用什么布局，也就是说布局被隐含了，这就需要自己去推演，比较麻烦。但是一般来说我们会使用一种叫混合布局的思路，即如果是向量或者矩阵对标量求导，则使用分子布局为准，如果是标量对向量或者矩阵求导，则以分母布局为准。对于向量对对向量求导，有些分歧。

1.4 分母布局的另一种求解方法

已知：

     

      

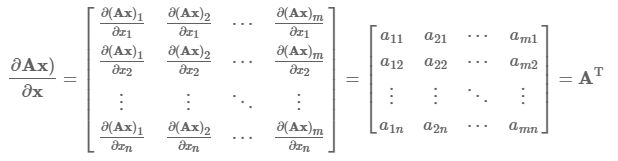
        对谁求导数，就以谁（分母）作为主序，得出结果。比如这里x是列向量，求Ax关于x求导数，那么对x的每个分量分别求偏导数(写成一行)，然后整理排成一列（同x一样是列向量）。 

        

        

同理有：

        关于x的转置x.T求导数，x.T是行向量，那么Ax分别对x.T向量中的分量求偏导（写成一列），然后整体排成一行（同x.T是行向量）。

1.5 总结

2 基本的求导规则

         这一部分，我们将看到一些基本的求导规则，这些与其说是规则，倒不如说是定义。因此这一部分是需要好好理解并且记忆的。

        因为向量和标量都可以表示成简单的矩阵形式，所以这里我们使用“矩阵”来泛化的表示所有含义。我们使用黑体字母来表示向量，而黑体大写字母表示矩阵。

2.1 向量对标量求导（相对于数量变量的微分，即自变量是数量变量）

2.1.1 定义

      首先是向量 y 对标量 x 求导，我们假定所有的向量都是列向量，

         

    在分子布局下，

       

      即：

      而在分母布局下，

         

在接下来的部分将默认使用分母布局，除非是在一些很特殊的情形，这些到时候再详述。

2.1.2 运算法则

           

2.2 标量 y 对向量 x 求导（数量函数相对于向量的微分）

2.2.1 定义

分母布局：

        

2.2.2 运算法则

               

2.2.3 示例

（1） 

解：

     

       注意到，标量对向量求导和向量对标量求导刚好反过来。

2.3 向量对向量求导

2.3.1 定义

       

        

  （1）m 维向量函数对 n 维列向量 X 的导数（分子布局）：

        

  （2）m 维向量函数对 n 维列向量的导数（分母布局）：

        

      

2.3.2 运算法则

            

         

        

                             最后一个式子的证明见2.3.3（1）。

                           

                            

2.3.3 示例

（1）证明

（2）

         解：

             

             

              注：移乘做除和移除做乘的意思，移到等号的另一边时，要改变运算符号。

（3）

         

        

（4）

        bi 为 n 维列向量。

        

         

        其中每一个列向量

        因此有：

         

（5）

        根据：

                

          即：

          

         

（6）

           

2.4 标量对矩阵求导

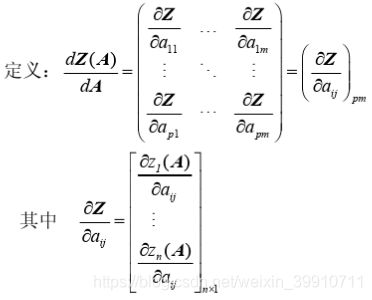
2.4.1 定义

         

2.4.2 示例

（1）

          

2.5 矩阵对标量求导（分子布局）

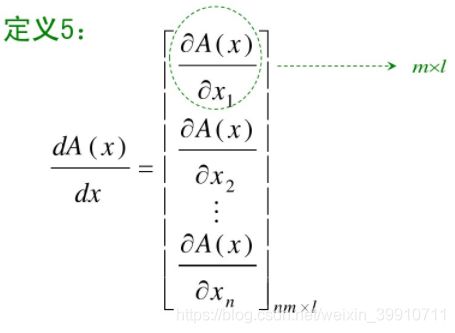
2.5.1 定义

        对于 n × m 维矩阵函数，

         

          

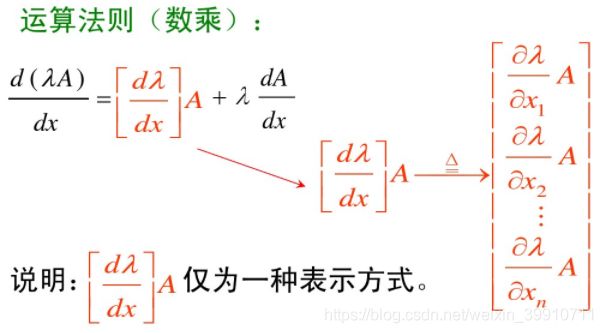
2.5.2  运算法则：

                   

                  

                  最后一个式子的证明见2.5.3（2）。

2.5.3 示例

（1）

          

      解：

            

             

（2）证明

        设A(t)和B(t)分别为 n × m 和 m × l 矩阵：

                  

            因此：

                     

        事实上，直观上看，凡是对标量求导，结果的形式都要转置，而标量对向量和矩阵求导则位置保持不动。这样总结方便我们记忆。

2.6 矩阵函数相对于向量的微分

2.6.1 定义

           

            

                  

              

2.6.2 运算法则

              

          

          

2.7 向量相对于矩阵函数的微分（分母布局）

        设函数，

        

2.8 矩阵函数相对于矩阵函数的微分

2.8.1 定义

        设函数：

        

        

2.8.2 示例

           

解：根据矩阵乘法

         

根据数量函数导数的定义，

2.9 复合函数的微分

（1）公式一

        

        

（2）公式二

         

             

总的来说，涉及矩阵和向量的求导不外乎五大类别，

1. 向量对标量
2. 标量对向量
3. 向量对向量
4. 矩阵对标量
5. 标量对矩阵

3 维度分析（针对前三类问题）

        接下来我们来看一些常见的求导，，于是利用向量对向量求导法则，有

       

理论上对于任意的表达式，我们都可以通过定义出发，利用上面这种形式推导得到。

但是对于一些复杂的求导，这个时候恐怕逐项展开分析就不是很靠谱了。

我们先来看求导分类的前三类，对于这三类问题，我们来看一个非常强大的方法，通过分析维度来得到结果。

考虑 , A 与 x 无关，所以 A 肯定可以先提出求导式，至于去哪了暂时不清楚。

        假如，我们知道最后结果肯定和 有关，注意到  ,于是 A 只能转置以后添在后面，因此

             

        同样对于，a 和 x 相关的标量，假定 u∈R(m×1)，x∈R(n×1)，根据乘积法则（非精确版本），前一个部分肯定是，后一部分为 和 u 的某种形式的积，分析维度发现只能是  。

于是

     

        我们发现，虽然乘积法则的精准形式无法应用于矩阵求导中，然而这种非精确的乘积法则可以准确的告诉我们哪些项一定会出现在结果中，然后通过分析维度，我们就可以写出结果。

3.1 例一

  ，其中 A 和 x 无关，

为了分析这个问题，我们考虑一个更一般的问题，

    

我们利用非精确的乘积法则，可以将这个分成两部分

    

于是结果和两部分相关，一个是，另一个是，

同样通过分析维度，我们可以得到   。

因此  

3.2 例二

   

改写成： 

注意到：   

所以(注意到  )：

               

4 矩阵的迹求导（微分形式）（标量对矩阵求导）

        接下来看五种类型中剩下的两类，在实际的问题中，主要是矩阵的迹对矩阵的求导问题。 正如我们在前面看到的，在矩阵的求导中，不存在精确的乘积法则，我们只是通过非精确的乘积法则分析出单项式中含有的项，再通过维度分析得到结果。 但是，有一种情形下，乘积法则是精确成立的，我们现在就来看这一种情形——迹的微分。因为在微分形式下，

• 乘积法则成立
• 迹和微分可交换

        所有之前的结果转置一下，就得到了分子布局下的结果。

        接下来请注意，当我们谈论微分的时候，只有在分子布局下才是有意义的。

        （Warning：微分只有分子布局，没有分母布局）

首先我们指出：

        

等价于：

注意这是分子布局下的，对应分母布局下应该为：  

为了方便记忆，防止混淆，我们干脆将和直接等同起来。

于是所有的迹形式对矩阵的求导都先转化为微分形式，比如

        

         （该矩阵求导为标量对矩阵求导，可以通过矩阵展开证明。）

先回忆一些非常有用的迹的性质：

• 矩阵的迹和转置的迹相同（转置性质）
• 矩阵乘积的迹和矩阵乘积轮换对称后的迹相同（循环排列）

考虑

所以

常用的矩阵的迹的相关公式：

         

        

   证明：

         定理1：

         证明： 由于迹为矩阵主对角线的元素和，而矩阵的第个主对角线元素可表示为: . 即的行元素与的列元素的向量积。 因此，由如下结论: 

         定理2：

         证明： 或当作整体，证明与定理1相同。

         定理3：

         证明： 由于  
                     那么，因此，

         定理4：

        定理5： 

        证明： 对于存在多处情况，利用分步求导公式 
 
                    并基于定理1、定理3和4，可得， 

5 推导公式

5.1 例一

    对任意行向量，都有

同时注意，如果 w 表示一个列向量，则

          

5.2 例二

       A表示一个矩阵，其中表示行向量，，都有

       

       (这里用到了上面的3.1的公式)

B 表示一个矩阵，其中 ，表示列向量(注意这个和刚才不同,这里表示列向量)

           

都有

          

5.3 例三

还有些较为复杂的推导，例如：

（见3.1）

（见3.2）

6 应用到线性回归

        考虑一个简单的线性回归的例子，我们有X，它是一个n x m的矩阵，也就是有 n 个实例，每个实例有m个特征，这里我们假定 n>m 它的标签是要 y，那么就是一个 nx1 的列向量，我们需要调整的参数就是w，它是一个mx1的列向量，那么我们预测的结果就是   
          

        相应的损失函数就是   ，然后我们计算梯度。

6.1 通过链式法则

        这个式子类似于，先把 y−Xw 看成整体,得到2(y−Xw)，然后计算（y−Xw ）对 w 的导数，其中 y 里面没有包含w ，结果为0，然后−wX 对 w 的导数得到 ，最终结果就是

                

6.2 将式子拆开然后每个项求导

             

        注意中不含 w ，求个导就没了,然后依次对每项求导结果如下：

              

此时零导数等于0，得到结果：

               

7 “前导不变后导转置”向量求导法则

8 矩阵导数的基本运算规律

8.1 转置

        矩阵转置的导数和矩阵的导数是一样的，因为转置并不改变值的大小。

        矩阵的转置和加减乘除一样，也是一种运算，且满足下列运算规律（假设运算都是可行的）：

       

8.2 矩阵的基本运算

1、加法：矩阵的加法满足下列运算律(A，B，C都是同型矩阵)：

2、数乘：矩阵的数乘满足以下运算律：

      

3、乘法：两个矩阵的乘法仅当第一个矩阵A的列数和另一个矩阵B的行数相等时才能定义。如A是m×n矩阵和B是n×p矩阵，乘积C是一个m×p矩阵：

          

https://xuehy.github.io/blog/2014/04/18/2014-04-18-matrixcalc/index.html

7

https://en.wikipedia.org/wiki/Matrix_calculus

矩阵求导_布鲁格若门的博客-CSDN博客

矩阵的迹求导：

矩阵求导和迹 - 作业部落 Cmd Markdown 编辑阅读器

【机器学习】汇总详解：矩阵的迹以及迹对矩阵求导_来自文家市的那个小孩的博客-CSDN博客_矩阵的迹怎么求

矩阵微分法：

矩阵微分法 - 百度文库

矩阵微分(变分)法 - 百度文库

数学-矩阵计算（4）两种布局_仙守的博客-CSDN博客_分子布局

矩阵论（八）：矩阵微分与矩阵求导_exp(i)的博客-CSDN博客_矩阵微分与矩阵求导

机器学习中的矩阵向量求导(一) 求导定义与求导布局 - 刘建平Pinard - 博客园

总结：数学-矩阵计算（4）两种布局_仙守的博客-CSDN博客_分子布局