Describing like Humans: on Diversity in Image Captioning

Describing like Humans: on Diversity in Image Captioning

原文地址

时间：2019 CVPR

Intro

当前的image captioning模型虽然在各种指标（BLEU METEOR ROUGE CIDEr）上超过了人类水平，但是这些以accuracy为度量甚至是训练目标的模型缺少了diversity，为此，本文提出了一个度量图片diversity的metric。

diversity包括三个层次：

• word diversity指仅仅替换某个词而不影响语义
• syntactic diversity指在词序、词组和句子结构上的不同
• semantic diversity值描述的概念、细节、主体、客体上的不同

本文主要衡量的就是semantic diversity

Motivation

• 一张图片胜过千言万语，图片中包括了各种不同的概念，因此对它的描述是多样性的
• 仅仅注重accuracy会导致模型产生常见的短语来避免错误
• diversity可以度量captioner的variance

Measuring Diversity of Image Captions

为了度量一个caption集合$\mathcal{C}=c_1,c_2,...,c_m$，需要考虑两Gee方面：accuracy和diversity，对于accuracy，传统方法是计算平均相似度得分，对于diversity，我们会考虑caption集合$\mathcal{C}$中成对的相似度

Latent Semantic Analysis

latent semantic analysis（LSA）是一个线性模型，被广泛用于information retrieval中。LSA考虑co-occurrence的信息（words或者n-grams），然后使用奇异值分解来得到不同topic的低维的表示，将LSA应用在caption set中，更多的topic则意味着更多的diversity，为了使用LSA，首先要将每个caption用向量表示，这里使用bag-of-words（BoW），然后在下一小节使用CIDEr将它kernelize

给定一个caption集合$\mathcal{C}=c_1,c_2,...,c_m$和一个字典$\mathcal{D}=w_1,w_2,...,w_d$，我们用词频来表示一个caption $c_i$,${\mathbf{f}}_{\mathbf{i}}=[f_1^i,...,f_d^i{]}^T$，其中$f_j^i$表示词$w_j$在$c_i$中出现的频率，从而caption集合$\mathcal{C}$可以表示为word-caption矩阵$M=[f_1,...,f_m]$???（没考虑词序）

通过SVD分解，$M=US{V}^T$，$S=diag({\sigma }_1,...,{\sigma }_m)$是对角矩阵，其中的每个奇异值都表示了topic的强度，如果$\mathcal{C}$中只有一个caption，则${\sigma }_1=1,{\sigma }_i=0,i>1$，如果每个caption不一样，则所有奇异值是一样的（？怎么就一样了），因此，$r=\frac{{\sigma }_1}{{\sum }_{i=1}^m{\sigma }_i}$则表示了caption的diversity，因为$r$在[1/m,1]之间，因此我们可以把他映射到[0,1]，$div=-{\log }_m(r)$

考虑矩阵$K=M^{T}M$，其中每个元素$k_{ij}=f_i^T{f}_j$是BoW向量$f_i$和$f_j$的内积，因为$f_i$的维度可能很大，更好的计算方法是使用特征值分解$K=V\Lambda V^T$，其中$\Lambda =diag({\lambda }_1,...,{\lambda }_m)$，是$K$特征值，则${\sigma }_i=\sqrt{{\lambda }_i}$，注意$K$是一个核矩阵，这里使用的是线性核

Kernelized Method via CIDEr

上一节的diversity度量方法忽略了词组和句子的结构，为了解决这个问题，这里使用n-gram或p-spectrum核，映射函数使用n-gram将caption空间$C$映射到特征空间$F$，

其中$f_i^n(c)$是第i个n-gram的频率，$D^n$是n-gram的字典

CIDEr现将caption映射到带权特征空间$F$，${\Phi }^n(c)=[w_i^n{f}_i^n(c){]}_i$其中$w_i^n$是第i个n-gram的IDF，CIDEr得分是每个n的余弦相似度

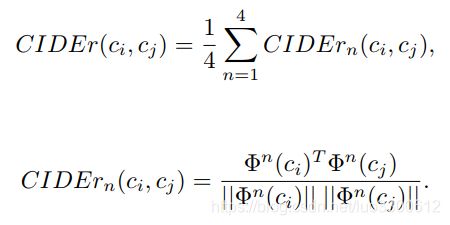
其中feature space被${\Phi }^n(c)$映射

因为CIDEr可以被解释为一个核函数，我们可以重新考虑LSA中的矩阵$K$，通过使用$k_{ij}=CIDEr(c_i,c_j)$，基于CIDEr的diversity可以通过核矩阵的特征值KaTeX parse error: Expected '}', got '\lamdba' at position 16: {\lambda_1,...,\̲l̲a̲m̲d̲b̲a̲_m}计算为$r=\frac{\sqrt{{\lambda }_1}}{{\sum }_{i=1}^m\sqrt{{\lambda }_i}}$，$div=-{\log }_m(r)$

Conclusion

本文设计了一个度量image caption模型的diversity的制表，它基于CIDEr根据核矩阵计算特征值得到