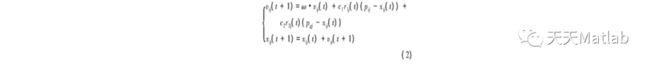【三维路径规划】基于模拟退火算法结合粒子群算法多无人机三维路径规划含Matlab源码
1 简介
粒子群优化算法 (particle swarm optimization, PSO)是Kennedy和Eberhart于1995年提出的一种群体智能仿生算法, 在解决一些典型的函数优化问题时, 能够取得比较好的优化结果。
**1 无人机航迹规划模型
1.1 航迹表示方法**
一般地, 无人机航迹规划的空间可以表示为某三维坐标系下所有点的集合{ (x, y, z) |xmin≤x≤xmax, ymin≤y≤ymax, zmin≤z≤zmax}, 其中x, y可以表示为该节点在飞行水平面下的坐标, 也可以表示为该点的经纬度, z为高程数据或海拔高度。航迹规划的目的是获得无人机在该空间中的飞行轨迹, 生成的航迹可表示为三维空间的一系列的点{PS, P1, P2, …, Pn-2, PG}, 相邻航迹点之间用直线段连接。
**1.2 航迹代价函数**
在航迹规划中, 常采用经过适当简化的航迹代价计算公式
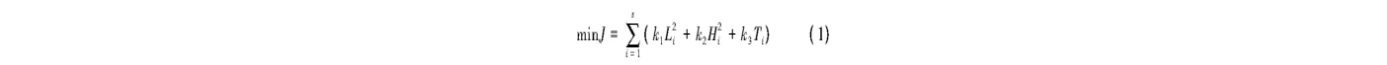
式中, s表示航迹段数, Li表示第i段航迹长度, 该项代表距离代价。Hi表示第i段航迹的平均海拔高度, 该项代表高度代价。Ti为第i段航迹的威胁指数, 该项代表威胁代价。k1、k2、k3分别是距离代价、高度代价和威胁代价的权重值, 权重的选取与飞行任务要求相关。
**2 基本粒子群算法**
粒子群算法初始化为一群数量为N的随机粒子 (随机解) , 在D维空间中通过重复迭代、更新自身的位置以搜索适应度值最优解。粒子的位置代表被优化问题在搜索空间中的潜在解。在每次迭代中, 粒子通过跟踪2个“极值”来更新自己的速度和位置:一个是粒子自身目前所找到的最优解, 即个体极值;另一个是整个粒子群目前找到的最优解, 即全局极值。粒子i (i=1, 2, …, N) 在第j (j=1, 2, …, D) 维的速度vij和位置xij按如下格式更新:
式中, ω为非负数, 称为惯性权值 (惯性因子) , 描述了粒子对之前速度的“继承”, 即体现出粒子的“惯性”;c1和c2为非负常数, 称为学习因子 (加速因子) , 体现了粒子的社会性, 即粒子向全局最优粒子学习的特性;r1和r2为 (0, 1) 之间的随机数;pi= (pi1, pi2, …, pi D) 表示粒子i的个体极值所在位置;pg= (pg1, pg2, …, pg D) 表示所有粒子的全局极值所在位置。
速度更新公式的第一项, 反映粒子当前速度的影响, 每一个粒子按照惯性权值的比重沿着自身速度的方向搜索, 起到了平衡全局的作用, 同时避免算法陷入局部最优;第二项体现了个体最优值对粒子速度的影响, 即粒子本身的记忆和认识, 使得粒子具有全局搜索能力。第三项则反映群体对个体的影响, 即群体间的信息共享起到加速收敛的作用。
2 部分代码
%% PSO 三维路径规划clc,clear , close allfeature jit off%% 模型基本参数% 载入地形 矩阵filename = 'TestData1.xlsx' ;model.x_data = xlsread( filename , 'Xi') ;model.y_data = xlsread(filename, 'Yi') ;model.z_data = xlsread( filename , 'Zi') ;model.x_grid = model.x_data(1,:) ;model.y_grid =model.y_data(:, 1) ;model.xs = 10 ; %起点 相关信息model.ys = 90 ;model.zs = interp2( model.x_data , model.y_data, model.z_data , ...model.xs , model.ys ,'linear' ) ; % 高度为插值得到model.xt = 130 ; % 终点 相关信息model.yt = 10 ;model.zt = interp2( model.x_data , model.y_data, model.z_data , ...model.xt , model.yt , 'linear'); % 高度为插值得到model.n= 5 ; % 粗略导航点设置model.nn= 80 ; % 插值法获得的导航点总数model.Safeh = 0.01 ; % 与障碍物的最低飞行高度% 导航点 边界值model.xmin= min( model.x_data( : ) ) ;model.xmax= max ( model.x_data( : ) ) ;model.ymin= min( model.y_data( : ) ) ;model.ymax= max( model.y_data( : ) ) ;model.zmin= min( model.z_data( : ) ) ;model.zmax =model.zmin + (1+ 0.1)*( max( model.z_data(:) )-model.zmin ) ;% 模型的其他参数model.nVar = 3*model.n ; % 编码长度model.pf = 10^7 ; % 惩罚系数% 障碍物 位置坐标及半径model.Barrier = [10,60 , 8 ;40, 50,660, 50 , 5100, 30, 8 ] ;model.Num_Barrier = size(model.Barrier , 1 ); % 障碍物的数目model.weight1 = 0.5; % 权重1 飞行线路长度权重model.weight2 = 0.3; % 权重2 飞行最低高度相关权重model.weight3 = 0.2; % 权重3 最大攻角约束 权重%% 算法参数设置for i=1:3param.MaxIt = 200; % 迭代次数param.nPop= 30; % 种群数目param.w=1; % 权重param.wdamp=0.99; %退化率param.c1=2 ; % Personal Learning Coefficientparam.c2=2 ; % Global Learning Coefficient% 局部搜索部分参数param.MaxSubIt= 0; % Maximum Number of Sub-iterations ( 内循环迭代次数 )param.T = 4000; %param.alpha1=0.99; % Temp. Reduction Rateparam.ShowIteration = 200; % 每过 多少次迭代显示一次图%% 运行算法CostFunction=@(x) MyCost(x,model); % 设置目标函数[ GlobalBest , BestCost ] = pso( param , model , CostFunction ) ;end
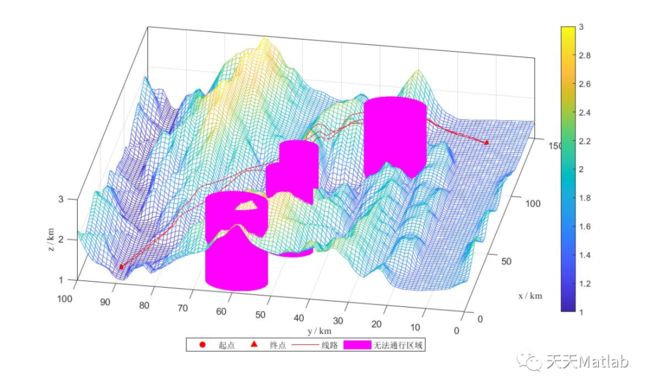
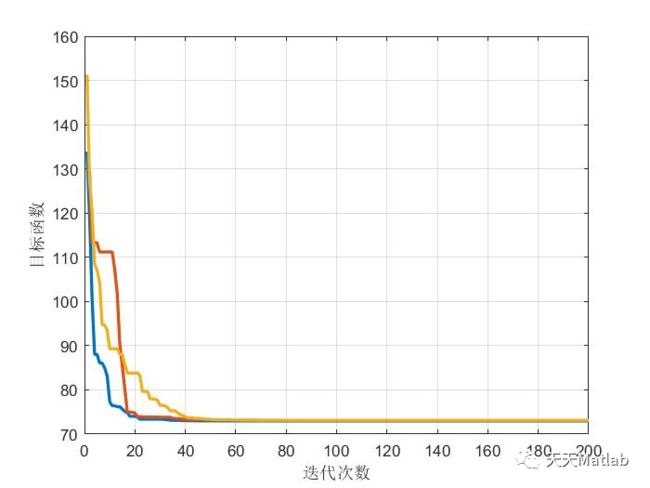
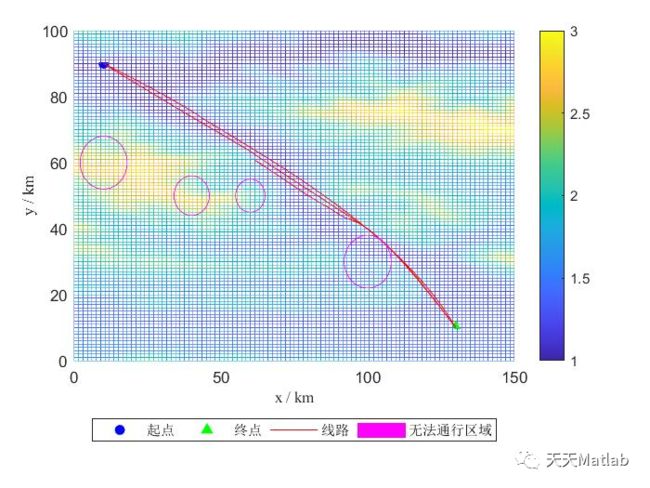
3 仿真结果
4 参考文献
[1]江冰, 郭彭. 基于粒子群算法的三维无人机路径规划方法及规划系统:, CN112230678A[P]. 2021.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。