tikhonov正则化 matlab_机器学习中的各种范数与正则化

机器学习中的各种范数与正则化

对于统计机器学习算法一般为缓解过拟合现象的发生需要在进行正则化操作,通过正则化以偏差的增加换取方差的减小，因此优秀的正则化操作即是在保证方差较小的情况下，偏差尽可能的小。有关偏差与方差的介绍可以参考我的这篇笔记

PoderLee：Bias - Variance Dilemma(偏差-方差窘境)​zhuanlan.zhihu.com

最常见的方法即为在损失函数中引入矩阵范数，以对模型的复杂程度做出惩罚，即模型的权值参数（一般不考虑惩罚偏置，这主要是因为惩罚偏置首先不会有明显效果，其次惩罚偏置可能会造成模型欠拟合），其目标函数一般如下式所示：

上式中，第一项即为经验风险，第二项即为正则化项。其中

，为调整两者之间关系的系数。当

时，则表示无正则化项，

越大则表示对应正则化惩罚越大。

• 范数正则化

这里我们假设模型的偏置参数均为0，则参数

即为

，因此其目标函数为：

对上式求其梯度有：

使用梯度下降法更新权重

，则

将向负梯度方向收敛，如下：

从中可以看出每次权值

更新时都将乘以

，该常数因子小于0，即权重将会逐渐收缩，趋近于0。

进一步地，这里令

（将

简记为

）,即

为损失函数

取得最小训练误差的权值。并在

的邻域对损失函数

做二次近似（泰勒展开）,记为

，如下：

上式中

为

在

处计算的Hessian矩阵，且该矩阵为半正定矩阵。由上述知，

为损失函数的最优解，因此

的梯度将为0，即式（6）对

求偏导为0，如下所示：

记

为最优权值

，将式（7）代入式（4）：

故：

（由于Hesian矩阵为半正定矩阵，故其为实对称阵。因此有

）

当

趋向于0时，

将趋近于

。我们将实对称Hesian矩阵

分解为一个对角矩阵

和一组特征向量的标准正交基

，因此有

，代入式（9）,可得

从上式中可以看出经过正则化后，权重

将会沿着由

特征向量所定义的轴缩放未经标准化的损失函数最优解

。具体来说，我们会根据

因子收缩与

第

个特征向量对齐的

的分量。如下图所示。

图1. 特征向量作用效果图

上图为特征向量的作用效果图，这里矩阵有两个标准正交特征向量，对应的特征值分别为

和

。其中左图为所有单位向量

集合构成的单位圆。右图为特征值的拉伸结果。

由于特征向量的缩放因子为

，故沿着特征值较大的方向（如

）正则化影响较小。而

将会收缩至几乎为零。因此

范数将使模型的参数趋近于0附近。

通过

正则化，在显著减小目标函数方向上的参数会被相对完整的保留，而对于无助于目标函数减小的方向（对应Hessian矩阵较小的特征值），其参数的改变将不会显著参加梯度，因此其在训练过程中会因正则化项而衰减至0。

此外，在线性回归的平方误差损失函数中引入二范数，即在原来逆矩阵的基础上加入对角阵，使得矩阵求逆可行，同时缓解过拟合的问题。而由于加入的对角矩阵，其就像一条“山岭”一样，因此，

在统计学中也被称为岭回归或Tikhonov正则。

线性回归目标函数一般为：

固有：

即：

当引入

正则项后，目标函数变为：

则：

此即为岭回归。

上式中第（1）项

即为线性回归标准最小二乘项，第（2）项

即为正则化项，为一对角阵。

另外从另一个角度理解，当

非正定时（某些参数线性相关），其无法求逆。此时解决的方法一般包括两种：（a）通过PCA构建线性无关组，进行降维处理，删除无关特征，求逆；（b）二范数正则化，即通过增加取值较小的对角阵使得矩阵求逆可行。由于PCA方法处理后其剔除了一些贡献程度较小的特征，而二范数只是将部分无关特征权值缩放置0附近，因此二范数也被称为Soft-PCA。

• 范数正则化

范数形式如下：

如上式所示，

范数为各参数的绝对值之和。（

范数求导、优化困难，因此较

范数相比使用较少）对于，

范数其目标函数如下所示：

其对应的梯度如下：

上式中，

为符号函数，其取值结果只与个权值

的正负号有关。

同理，这里令

，我们可以将

正则化目标函数的二次近似解分解为关于各参数求和的形式：

对每一维

求梯度，以最小化式（14）。由于

为

的最优解，因此有

，故：

即：

对

的正负号分类讨论，则上式将等价于：

当

时，会有两种结果：

a.

。此时式（16）的最优值为

。

b.

。此时则有

，即

在此方向上向0收缩

个距离。

同理，当

时，

也将等于0或向0收缩。

与

范数相比，

范数正则化使得部分参数为0。因此，

范数会产生更稀疏的解，该性质已被大量应用于特征的选择机制。著名的LASSO回归即将

范数引入至线性模型中，并使用最小二乘代价函数。通过

正则化使得部分权值为零，而忽略相应的特征。如图2所示。

图2. 一范数与二范数示意图

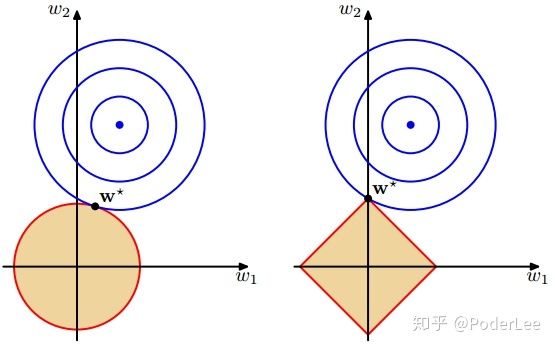
上图中，蓝色的圆圈表示原问题可能的解范围，橘色的表示正则项可能的解范围。而整个目标函数（原问题（损失函数）+正则项）有解当且仅当两个解范围相切。从上图可以很容易地看出，由于

范数解范围是圆，所以相切的点有很大可能不在坐标轴上，而由于

范数是菱形，其相切的点更可能在坐标轴上。因此其只有一个坐标分量不为零，其它坐标分量为零，即

的解是稀疏的。

范数正则化，模型权重服从高斯分布，

范数正则化，模型参数服从各向同性的拉普拉斯分布。即

正则化项

与通过MAP贝叶斯推断最大化对数先验项等价。此外，相较于

而言，采用

模型的鲁棒性较差（每次至零的权值均不相同）。

(拉普拉斯分布：

)

由于目标函数是关于

的最大化进行学习，因此可以忽略

。

• 范数

范数如下所示：

范数即为模型参数中不为0的数目。在实际问题中，模型一般较为复杂，参数数目较多，因此求解

范数为NP难问题，故一般不使用。在过去的前几年做压缩感知即稀疏表达时一般会使用0范数，但由于其优化困难因此会用1范替代。

• Frobenius范数

Frobenius范数如下所示：

从上式可以明显看出，矩阵的Frobenius范数就是将矩阵张成向量后的

范数。（在此就不做推导了）

各类范数一般作为各类机器学习模型权值的约束项（惩罚项）出现在目标函数中，训练过程以使得结构风险最小化，防止过拟合的发生。

此外有关泛化的其它方法如下：

• 数据增强

数据增强也能增加模型的泛化性能，如对图像的彩色通道进行一定程度的抖动（FancyPCA），对图像进行水平翻转（镜像处理），但这里需要注意的是水平翻转不应改变数据类别（如对于文字，字符的识别一般不会进行horizontal flipping）。

图像彩色通道随机抖动

水平翻转

• 随机噪声

随机噪声的注入也是一种正则化的方法，其等价于权值正则操作(Bishop,1995)。我们可以将噪声注入至模型的任意部分（当然一般选择将其添加至隐层而非输出），通过噪声的注入虽然无法保证能找到最优解，但我们可以将参数更新至一个相对平坦的区域，使其对于数据的随机扰动更加鲁棒。

• 标签平滑操作

在图像识别中，其标签一般为one-hot值，如[1,0,0,0,0]，而模型的预测输出结果一般为经过softmax处理后的概率值如[0.9,0.03,0.01,0.005,0.055]。这样在训练过程中,我们需要让网络尽可能的去拟合one-hot编码，此时将会导致weights的调整越来越大。故一种简单的想法是对label进行smoothing，如下：

上式中，

即为标签的随机噪声，通过引入平滑操作改变one-hot label使训练更加平稳。

Early Stopping

在网络的训练过程中，经常会遇到过训练的问题，即模型通过不断训练，其在训练集上的损失不断减小而验证集的误差将不断增加。

loss

从上图可以看出，Validation set loss呈现出一种非对称的"U"形，因此我们期望在validation loss上升前终止迭代，即early stopping。然而在实际的操作中我们一般是通过划分出一部分数据集在每个epoch中计算validation loss，其并非generalization，即其并不能solid的反映数据的整体情况，因此一般情况下是在loss没有较大下降时停止。Early stopping在实际训练中十分常见。

• Dropout

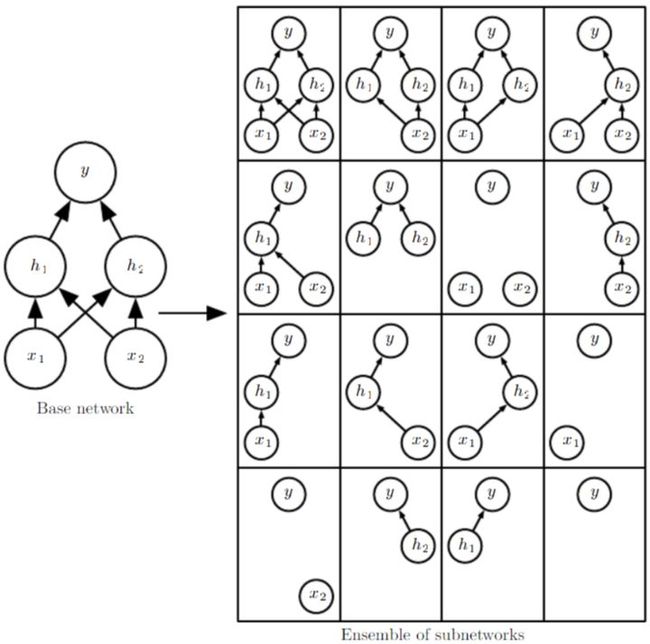
Dropout操作即在训练时随机将部分参数置零（一般为全连接层），在减少训成本的同时提高模型的泛化性能。Dropout本质上也可以理解为多个subnetworks的ensemble且不需要进行votes。此外对于较大规模的数据集，regularization operation对于generalization error 的减少效果并非十分明显，而Dropout则能有效减少计算代价，因此dropout更加实用。

• 对抗样本

对于图像的识别任务，虽然目前深度网在ImageNet上的精度已经超过了人类水平，但是我们只要在原始图片中掺杂一些随机的小扰动，对于人类其并不能察觉，而深度网络的输出将会变得十分的ridiculous，即fool network。因此我们可以利用对抗数据，进行对抗训练。

对抗样本

Reference

[1] Liang Wang. Regulaarization and Optimization. 中科院自动化研究所.