2022 电赛陕西省赛
一:题目:
声源定位跟踪系统(E题)
设计制作一个声源定位跟踪系统,能够实时显示及指示声源的位置,当声源移动时能够用激光笔动态跟踪声源。
- 设计并制作声音发生装置——“声源”,装置最大边长或直径不超过10cm,声源中心点B用红色或其他醒目颜色标识,并在B点所在的平面以B点为圆心,直径为5cm画圆圈,用醒目线条标识,该平面面向检测指示装置(图中A点)。(4分)
- 设计并制作一个声源定位检测装置,传感器安装在图1的 C区范围内,高度不超过1m,系统采用的拾音器或麦克风传感器数量不超过10个;在装置上标记测试参考点A,作为位置坐标的原点;装置上有显示电路,实时显示D区域内声源的位置,显示A、B两点直线距离γ和以A点为原点,AB在地面的投影与图1中心线的夹角θ,测量时间不超过5s,距离γ和角度θ的测值误差越小越好。(36分)
- 设计并制作一个声源指示控制装置,此装置和上述声源定位检测装置可以合为一体。也放置在图1的 C区,安装有激光笔和二维电动云台,能控制激光笔指向声源,定位计算过程中时,激光笔关闭,定位运算完成时激光笔开启。定位指示声源时,动作反应时间不超过10s,光点与B点偏差越小越好。(30分)
- 声源移动动态追踪:当声源摆放在地面,用细绳牵引,以0.2m/s左右的速度在D区移动时,激光笔光点指向B点,光点与B点偏差越小好,跟踪反应时间越短越好。(20分)
二:方案计划:
2.1【硬件选型】
Sipeed Maix Dock k210开发板:
Sipeed麦克风阵列模块:
激光模块:
按键:
2.2【基础架构】
刚开始将麦克风阵列模块平面放置进行尝试,但出来的声音数据处于整个屏幕的最下方,有一半数据被遮挡不见,所以放弃此方法。
后面将麦克风阵列垂直放置后发现接收到的数据偶尔会有偏移现象导致不准,所以开始尝试增加麦克风阵列的收音能力。
尝试通过增加桶装结构来增加收音功能,但由于桶太小,3m距离的两头顶点数据很少收到,所以最终还是使用垂直放置的方式。
2.3【各模块软件设计】
2.3.1 麦克风阵列软件设计:
依据官方给出的声源定位历程如下所示:
#导入MIC_ARRAY和LCD模块
from Maix import MIC_ARRAY as mic
import lcd
#初始化模块
lcd.init()
mic.init()
while True:
#获取原始的声源黑白位图,尺寸 16*16
imga = mic.get_map()
#获取声源方向并设置LED显示
b = mic.get_dir(imga)
a = mic.set_led(b,(0,0,255))
#将声源地图重置成正方形,彩虹色
imgb = imga.resize(160,160)
imgc = imgb.to_rainbow(1)
#显示声源图
lcd.display(imgc)
mic.deinit()
问题:依据官方给的结果只能得出一张声场图,通过调用 get_dir 函数可以得到12个灯珠的强度。但是得不到具体的位置,只能令相应位置的灯珠亮。
通过在网上搜寻发现了一位大神所写的依据官方声源定位做处理得到相应X坐标,Y坐标,强度,角度的具体实现如下所示:
def get_mic_dir():
AngleX=0
AngleY=0
AngleR=0
Angle=0
AngleAddPi=0
mic_list=[]
imga = mic.get_map() # 获取声音源分布图像
imgb = imga.resize(160,160)
imgc = imgb.to_rainbow(1)
lcd.display(imgc)
b = mic.get_dir(imga) # 计算、获取声源方向
for i in range(len(b)):
if b[i]>=2:
AngleX+= b[i]*math.sin(i*math.pi/6)
AngleY+= b[i]*math.cos(i*math.pi/6)
AngleX=round(AngleX,6) #计算坐标转换值
AngleY=round(AngleY,6)
if AngleY<0:AngleAddPi=180
if AngleX<0 and AngleY > 0:AngleAddPi=360
if AngleX!=0 or AngleY!=0: #参数修正
if AngleY==0:
Angle=90 if AngleX>0 else 270 #填补X轴角度
else:
Angle=AngleAddPi+round(math.degrees(math.atan(AngleX/AngleY)),4) #计算角度
AngleR=round(math.sqrt(AngleY*AngleY+AngleX*AngleX),4) #计算强度
mic_list.append(AngleX)
mic_list.append(AngleY)
mic_list.append(AngleR)
mic_list.append(Angle)
a = mic.set_led(b,(0,0,255))# 配置 RGB LED 颜色值
return mic_list #返回列表,X坐标,Y坐标,强度,角度
经过测试,发现数据非常NICE,但是还是有些达不到本次赛题的具体要求(只能说我也是非常头疼了)。于是开始尝试追寻源头,获取最底层的数据,尽量往题目de要求靠近了:(。
与麦克风阵列有关的函数库为MIC_ARRAY:MaixPy/components/micropython/port/src/Maix at master · sipeed/MaixPy (github.com)
通过查看发现我们所使用的
get_map()函数内部只是把数据进行了一个拷贝,真正的数据来自thermal_map_data,定义如下:STATIC uint8_t thermal_map_data[256];,是一个静态变量。000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 093 191 000 000 000 000 000 000 000 000 000 000 000 000 000 204 243 109 000 000 000 000 000 000 000 000 000 000 000 000 000 000 255 146 146 000 000 000 000 000 000 000 000 000 000 000 000 000 122 219 076 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 ==================== 000 000 000 016 122 206 168 068 000 000 000 000 000 000 000 000 000 000 000 000 078 255 208 120 003 000 000 000 000 000 000 000 000 000 000 000 096 164 201 204 042 000 000 000 000 000 000 000 000 000 000 000 010 043 139 149 028 000 000 000 000 000 000 000 000 000 000 000 000 000 021 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000这个变量只使用过两次,一次是初始化的时候进行读取,一次是在调用
get_map()这个函数的时候进行处理。接下来就瞅瞅到底是如何调用数据的。在
Maix_mic_array_init(size_t n_args, const mp_obj_t *pos_args, mp_map_t *kw_args)函数中最后一行代码显示int ret = lib_mic_init(DMAC_CHANNEL4, lib_mic_cb, thermal_map_data);所以最原始的数据来自lib_mic_init这个函数,而这个函数在#include "lib_mic.h"函数库中。
lib_mic.h地址如下所示:https://github.com/sipeed/MaixPy/blob/master/components/kendryte_sdk/include/lib_mic.h,最终发现官方只给了lib_mic.a静态链接库。所以我们目前所能够获得的最原始的数据便是thermal_map_data这256个数据也就是16x16在屏幕上所能看到的音场图像 。
软件设计:
-
通过
mic.get_dir(imga)获得的音场图像我们可以通过如下所示获得255的最原始的数据点。imga = mic.get_map() # 获取声音源分布图像 imgb = imga.resize(200,200) for y in range(imgb.height()): for x in range(imgb.width()): print('%03d'%imgb.get_pixel(x, y), end=" ") print('\r\n', end=" ") return -
因为最终得到的是图像数据,所以我们可以通过处理图像的API来处理音频数据(嘻嘻),通过
find_blobs函数可以适当的降噪并得到超过一定阈值的色块儿。th = [(230, 255)] blobs = imgb.find_blobs(th, area_threshold=16, pixels_threshold=1, merge=True, x_stride=1, y_stride=1) #官方地址:https://book.openmv.cc/image/blob.html -
这里通过最简单的对每个色块的cx值进行平滑处理(每次增加一个因素)得到大体的最终像素的位置。
if blobs: meanlost = 0 for obj in blobs: if meanfound == False: meanfound = True for i in range(meancount): mean_x[i] = obj.cx() meanwriteindex = 0 else: mean_x[meanwriteindex] = obj.cx() meanwriteindex = meanwriteindex + 1 meanwriteindex = meanwriteindex % meancount allv = 0.0 allv = (allv / (meancount)) - 100 print("x:" + str(allv) + "y:" + str(obj.cy())) else: meanlost = meanlost + 1 if meanlost > 50: meanfound = False -
之前已经通过
imga.resize函数将最终的结果放大到200了,所以理论上平面上的像素的位置因该处于100与-100之间。根据3m的约束,100像素对应150cm,在完全线性情况下计算距离的时候只需要将得到的值乘以1.5便是边上的最终距离(当然这是不切实际的哈,需要与真是场合进行最终的拟合) -
通过测试如果将其中的最大与最小值进行去除后效果较为稳定
max_num = mean_x[1] min_num = mean_x[1] for i in range(meancount): if mean_x[i] > max_num: max_num = mean_x[i] if mean_x[i] < min_num: min_num = mean_x[i] allv = allv + mean_x[i] allv = allv - max_num - min_num -
根据上述所示最终拟合后的情况较为稳定,大概像素抖动差距为1左右
2.3.2 舵机软件设计:
串口舵机通过官方的协议发送相应的组帧数据便可到达相应的角度,这里设置360度对应于4096细分。封装结果如下所示:
#该函数将角度转换为步进电机的位置参数
#假定角度范围是0-180
def yiding(angle):
return int(4096 * (angle / 360.0))
#该函数生成控制帧
def create_control_message(angle):
step = yiding(angle)
lw = step % 256
hg = step>>8
buffer = bytearray(7)
buffer[0]=0x2A
buffer[1]=lw
buffer[2]=hg
buffer[3]=0
buffer[4]=0
buffer[5]=0xE8 #这里没有做调速的逻辑
buffer[6]=0x03 #直接将选定的参数写在代码里,可按需修改
return SendBuffer(7, buffer, 0x03)
#该函数根据角度调用相应函数生成控制帧
#然后通过uart对象发送控制帧
def control(uart, angle):
uart.write(create_control_message(angle))
uart.read()
def SendBuffer(length, buffer, cmd):
data = bytearray(length + 6)
data[0] = 0xff
data[1] = 0xff
data[2] = 0x01
data[3] = length + 2
data[4] = cmd
i = 0
sum = 0
while i < length:
data[5 + i] = buffer[i]
sum += buffer[i]
i += 1
data[length + 5] = ~(data[2] + data[3] + data[4] + sum)
return data
#引脚映射
fm.register(6, fm.fpioa.UART1_RX, force=True)
fm.register(7, fm.fpioa.UART1_TX, force=True)
#构造函数
uart = UART(UART.UART1, 115200, read_buf_len=4096)
2.3.3 矩阵键盘:
通过IO口进行控制:
fpioa = FPIOA()
fpioa.set_function(30, fpioa.GPIOHS0)
fpioa.set_function(31, fpioa.GPIOHS1)
fpioa.set_function(32, fpioa.GPIOHS2)
fpioa.set_function(33, fpioa.GPIOHS3)
fpioa.set_function(34, fpioa.GPIOHS4)
key_1 = GPIO(GPIO.GPIOHS0, GPIO.IN, GPIO.PULL_UP)
key_2 = GPIO(GPIO.GPIOHS1, GPIO.IN, GPIO.PULL_UP)
key_3 = GPIO(GPIO.GPIOHS2, GPIO.IN, GPIO.PULL_UP)
key_4 = GPIO(GPIO.GPIOHS3, GPIO.IN, GPIO.PULL_UP)
key_5 = GPIO(GPIO.GPIOHS4, GPIO.IN, GPIO.PULL_UP)
print("GPIO_init!")
2.4【问题总结】
上述麦克风阵列部分的软件设计虽然设想很好像素抖动并不巨大,但是当时只是测量了某些点,直到经过反复测量+1.5m — -1.5m的整体路径后…
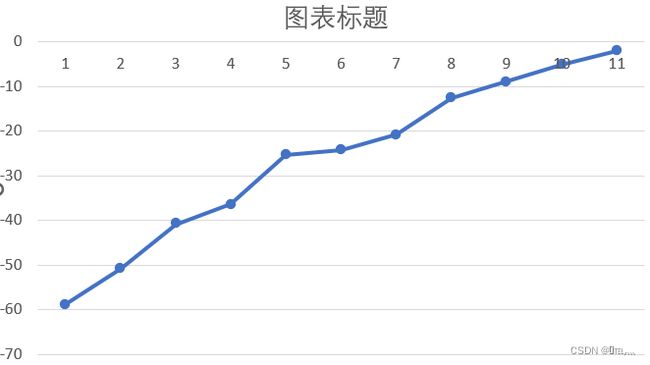
先上测试结果,如图所示为以15cm为间距测量的一个整体情况,发现在-75cm和-105cm之间麦克风阵列接收的值差距非常小几乎可以忽略…这岂不是代表6-7的像素结果最终需要对应到30cm emmm
| xvalue | realx_cm |
|---|---|
| -101.29 | -150 |
| -82.412 | -135 |
| -71 | -120 |
| -49.666 | -105 |
| -45.412 | -90 |
| -42.335 | -75 |
| -31.212 | -60 |
| -21.267 | -45 |
| -12.828 | -30 |
| -7.114 | -15 |
| 2 | 0 |
| 7.871 | 15 |
| 19.238 | 30 |
| 26.398 | 45 |
| 36.715 | 60 |
| 46.335 | 75 |
| 49.755 | 90 |
| 59.389 | 105 |
| 78.123 | 120 |
| 94.301 | 135 |
| 100.567 | 150 |
2.4.1【解决问题 —— 算法拟合的方式?】
刚开始的第一想法是认为算法太简单了可以通过拟合的方式导致结果好点,所以后面通过 TableCurve 2D 又再次对算法方面进行了优化。如图所示为原始数据,后面为重新修改算法后的对比图。
#三段数据通过傅里叶拟合后的代码已翻译为py
def evalfpoly_upper(order, x, c):
y = c[0]
x = (x-(-101.2900000000000))/(64.25307869540144)
i = 1
j = 1
while (j<=order):
y = y + c[j]*math.cos(i*x)+c[j+1]*math.sin(i*x)
j = j + 2
i = i + 1
return y
def x2cm_upper(x):
#xvalue,realx_cm
#X= x
#Y= y
#Eqn# 6846 Fourier Series Polynomial 6x2
#r2=0.9992520391742251
#r2adj=0.9978629690692147
#StdErr=4.024677208570474
#Fstat=890.6456102510882
#a= 18061.39806009811
#b= 3037.621539029955
#c= -32439.8924224331
#d= -23307.50404252103
#e= -4700.223775667663
#f= -4180.635182396415
#g= 13084.95904965044
#h= 5462.199382107961
#i= 2520.335507611479
#j= 992.9660259627591
#k= -1525.384832176511
#l= -216.0594810973499
#m= -201.9920503300485
c = [ \
18061.39806009811, \
3037.621539029955, \
-32439.89242243310, \
-23307.50404252103, \
-4700.223775667663, \
-4180.635182396415, \
13084.95904965044, \
5462.199382107961, \
2520.335507611479, \
992.9660259627591, \
-1525.384832176511, \
-216.0594810973499, \
-201.9920503300485 \
]
y = evalfpoly_upper(12, x, c);
return y
def evalfpoly_down(order, x, c):
y = c[0]
x = (x-(-101.2900000000000))/(16.43242956435201)
i = 1
j = 1
while (j<=order):
y += c[j]*math.cos(i*x)+c[j+1]*math.sin(i*x)
j = j + 2
i = i + 1
return y
def x2cm_down(x):
#xvalue,realx_cm
#X= x
#Y= y
#Eqn# 6841 Fourier Series Polynomial 1x2
#r2=0.9999494613096794
#r2adj=0.9998483839290382
#StdErr=0.2384450180034372
#Fstat=9892.91031254093
#a= -127.4956791753075
#b= -22.44558132774609
#c= 1.671278079513843
c = ( \
-127.4956791753075, \
-22.44558132774609, \
1.671278079513843 \
)
y = evalfpoly_down(2, x, c)
return y
def x2cm_inner(x):
#xvalue,realx_cm
#X= x
#Y= y
#Eqn# 6067 High Precision Polynomial Order 17
#r2=0.9999018183727648
#r2adj=0.9990181837276478
#StdErr=2.38117386446982
#Fstat=1797.212645936657
#a= -2.528288698078915
#b= 2.16076952420472
#c= 0.00582814018547617
#d= -0.002275948124670886
#e= -8.934730109710214E-05
#f= 6.811064374229286E-06
#g= 1.978340205779401E-07
#h= -9.293511972574285E-09
#i= -1.733939641774201E-10
#j= 6.179017571697362E-12
#k= 7.276632783720768E-14
#l= -2.128501488212396E-15
#m= -1.527417220941608E-17
#n= 3.833655302736212E-19
#o= 1.526021786343222E-21
#p= -3.395643131151524E-23
#q= -5.701345417693474E-26
#r= 1.157136867109389E-27
y = -2.528288698078915+x*(2.160769524204720+ \
x*(0.005828140185476170+x*(-0.002275948124670886+\
x*(-8.934730109710214E-05+x*(6.811064374229286E-06+\
x*(1.978340205779401E-07+x*(-9.293511972574285E-09+\
x*(-1.733939641774201E-10+x*(6.179017571697362E-12+\
x*(7.276632783720768E-14+x*(-2.128501488212396E-15+\
x*(-1.527417220941608E-17+x*(3.833655302736212E-19+\
x*(1.526021786343222E-21+x*(-3.395643131151524E-23+\
x*(-5.701345417693474E-26+x*1.157136867109389E-27))))))))))))))))
return y
def x2cm(x):
if x<-49.666:
return x2cm_down(x)
elif x > 49.755:
return x2cm_upper(x)
else:
return x2cm_inner(x)
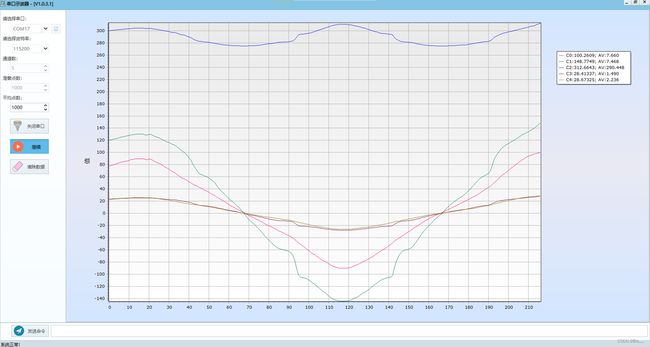
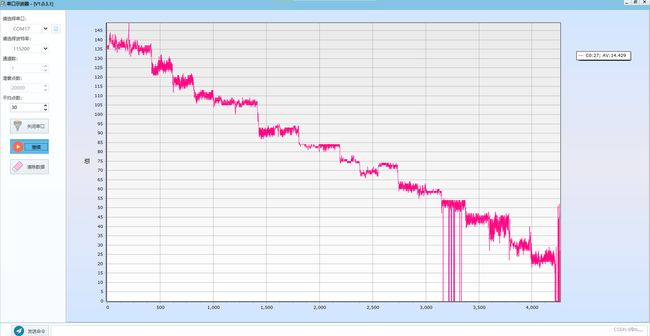
通过将数据导入到上位机方便进行查看和分析,蓝线为声源与接受装置之间的距离,红线为原始麦克风阵列的采样数据(像素数据),绿线为将麦克风阵列通过傅里叶变换拟合到3m距离的对应长度。发现结果并不十分稳定。
果然采集的数据不行再咋拟合都不行(服气)
2.4.2【解决问题 —— 改变音源播放的声音解决问题?】
【声音大小】
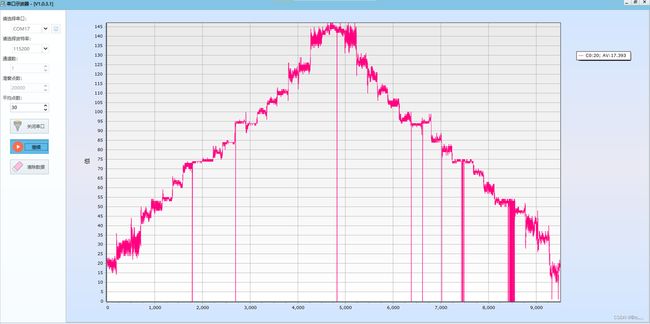
如图左边所示为播放小音量的结果,右边所示为播放大音量的结果,感觉好像并不差多少哎。所以排除声音大小的问题(0db -3db)
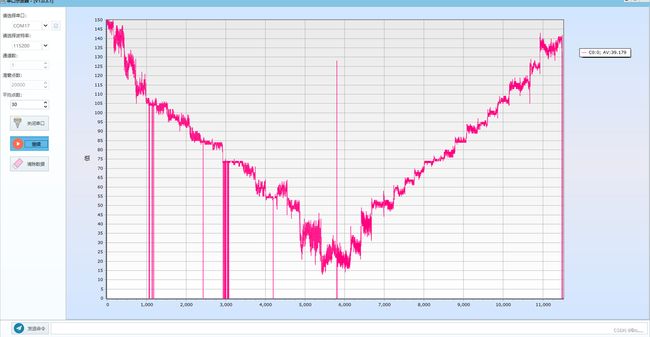
【声音频率的问题】
又找了两段不同频率的声音进行整体的测试,如图所示为测试结果,发现真的有用哎,不同的音频结果确实差距挺大的。但是都有各自的无法区分的区间 :?
于是开始了非常非常非常非常非常非常漫长的寻找音源的阶段,又过了一夜…最终有三个音频入选到决赛
【两种混音测试】
通过将两张音源进行混音再测试,发现测试情况并不理想,依旧有区分度不大的区间。
最终版 ->【三种交替测试】
最终通过测试,发现如果将三种声音进行依次排序播放,效果能达到最好,难以区分区间虽然依旧存在但效果最好
上传不上来嘞…
2.4.3【意外收获】
在进行音频测试的过程中发现,在模糊的点处,如果将周围的环境进行一定程度的干扰,例如在周围放置一块大的板子,有可能会打破当前的音场,导致这个点的区分度一下子上升,但是会导致另外一个问题,那就是这个模糊点会转移到其他的位置依旧存在…emm…
三:演示结果:
代码传送门:https://github.com/ChampDeLin/2022-DianSai-Provincial-level.git