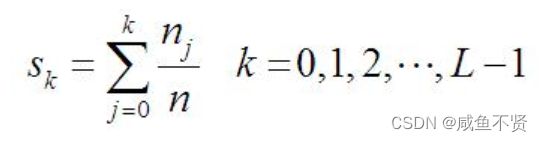Python计算机视觉之基本的图像操作和处理

目录

一、图像直方图

1.1 定义

1.2 代码实现

​ 二、高斯滤波

2.1 定义

2.2 原理

2.3 代码实现

三、直方图均衡化 

3.1 定义

3.2 原理

3.3 代码实现

---

一、图像直方图

1.1 定义

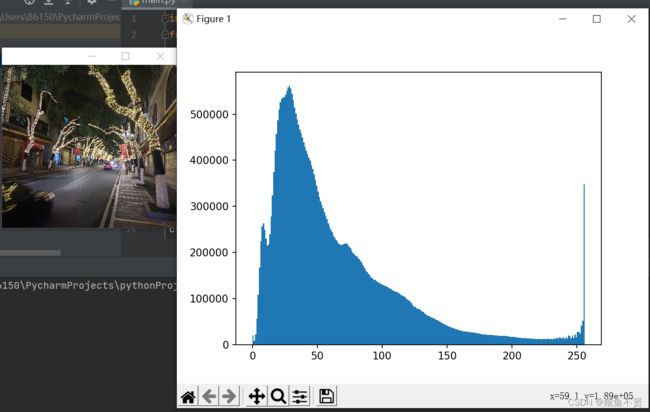
        图像直方图是反映一幅图像像素分布的统计图，其横坐标代表该图像像素的种类，可以是灰度的，也可以是彩色的。纵坐标代表每一种颜色值在该图像中的像素总数或者占所有像素个数的百分比。

        图像是由像素构成的，因此反映像素分布的直方图往往可以作为图像一个很重要的特征。

1.2 代码实现

方法一：利用matplotlib

import cv2 as cv
from matplotlib import pyplot as plt

def histogram_demo(image):
    plt.hist(image.ravel(), 256, [0, 256])#ravel函数功能是将多维数组降为一维数组
    plt.show()

src = cv.imread("WP2.jpg", 1)
cv.namedWindow("image",cv.WINDOW_NORMAL)
cv.imshow("image", src)
histogram_demo(src)
cv.waitKey(0)
cv.destroyAllWindows()

 方法二：利用Opencv的API

import cv2 as cv
from matplotlib import pyplot as plt


def image_hist(image): #画三通道图像的直方图
   color = ("blue", "green", "red")#画笔颜色的值可以为大写或小写或只写首字母或大小写混合
   for i, color in enumerate(color):
       hist = cv.calcHist([image], [i], None, [256], [0, 256])
       plt.plot(hist, color=color)
       plt.xlim([0, 256])
   plt.show()

src = cv.imread("WP2.jpg", 1)
cv.namedWindow("image",cv.WINDOW_NORMAL)
cv.imshow("image", src)
image_hist(src)
cv.waitKey(0)
cv.destroyAllWindows()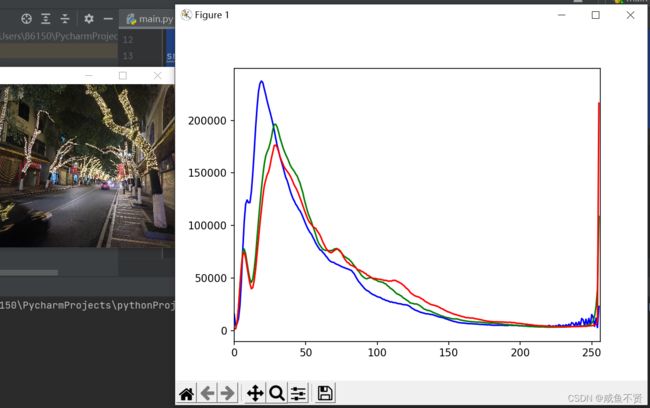

 二、高斯滤波

2.1 定义

        高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理和计算机视觉的减噪过程。

        那么，什么是高斯噪声呢？

        首先，噪声在图像当中常表现为一引起较强视觉效果的孤立像素点或像素块。简单来说，噪声的出现会给图像带来干扰，让图像变得不清楚。
        高斯噪声就是它的概率密度函数服从高斯分布（即正态分布）的一类噪声。如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。高斯白噪声的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。

 2.2 原理

        图像大多数噪声均属于高斯噪声，因此高斯滤波器应用也较广泛。

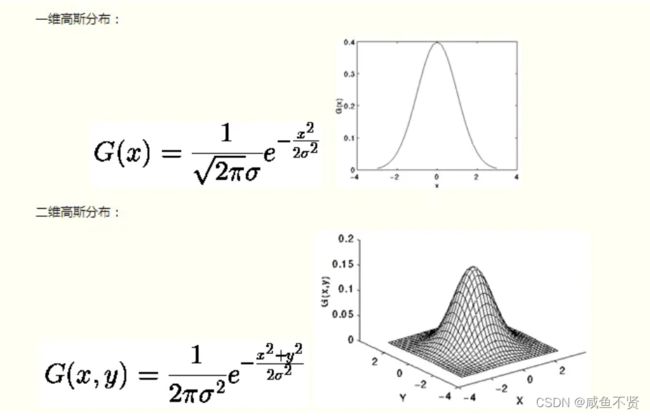
         高斯滤波器是根据高斯函数的形状来选择权值的线性平滑滤波器。

高斯函数： 

注：σ的大小决定了高斯函数的宽度。 

高斯核：

        理论上，高斯分布在所有定义域上都有非负值，这就需要一个无限大的卷积核。实际上，仅需要取均值周围3倍标准差内的值，以外部份直接去掉即可。
        高斯滤波的重要两步就是先找到高斯模板然后再进行卷积，模板（mask在查阅中有的地方也称作掩膜或者是高斯核）。所以这个时候需要知道它怎么来？又怎么用？
举个例子：
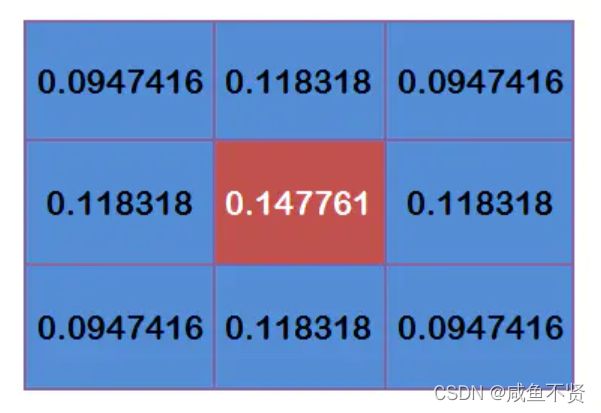
        假定中心点的坐标是（0,0），那么取距离它最近的8个点坐标，为了计算，需要设定σ的值。假定σ=1.5，则模糊半径为1的高斯模板就算如下

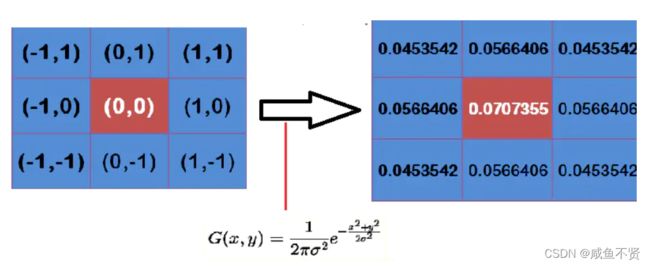
        这个时候我们我们还要确保这九个点加起来为1（这个是高斯模板的特性），这9个点的权重总和等于0.4787147，因此上面9个值还要分别除以0.4787147，得到最终的高斯模板。

高斯滤波计算：

        有了高斯模板，那么高斯滤波的计算便顺风顺水了。
举个例子：
        假设现有9个像素点，灰度值（0-255）的高斯滤波计算如下：

        将这9个值加起来，就是中心点的高斯滤波的值。
        对所有点重复这个过程，就得到了高斯模糊后的图像。 

        可以简单地理解为，高斯滤波去噪就是对整幅图像像素值进行加权平均，针对每一个像素点的值，都由其本身值和邻域内的其他像素值经过加权平均后得到。

        综上高斯滤波的操作可以总结为：用一个用户指定的模板（或称卷积、掩膜）去扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

2.3 代码实现

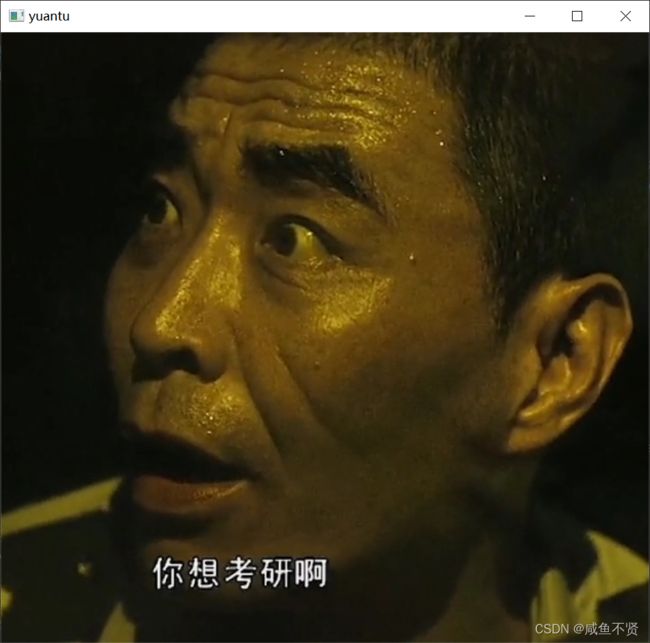
import cv2

img = cv2.imread('KY.jpg')
cv2.imshow('yuantu',img)
# (9, 9)表示高斯滤波器的长和宽都为9，2.8表示滤波器的标准差
out = cv2.GaussianBlur(img, (9, 9), 2.8)
cv2.imshow('result', out)
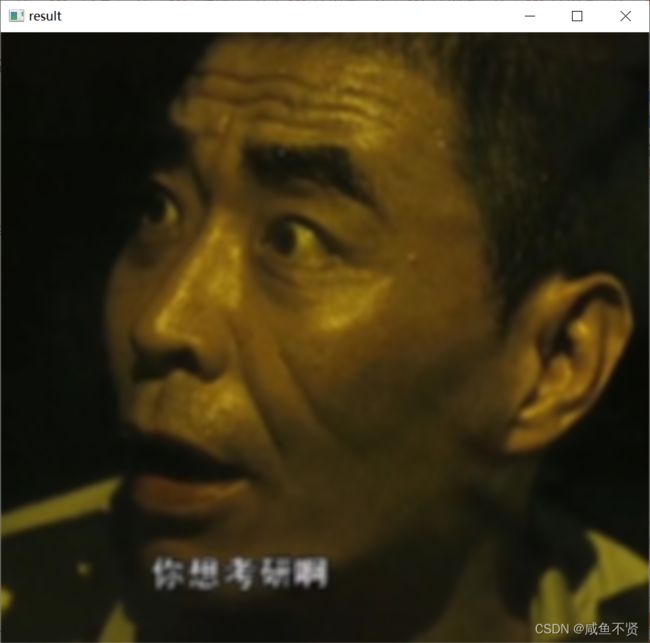
cv2.waitKey(0)
cv2.destroyAllWindows()

原图：

高斯滤波处理后：

三、直方图均衡化 

 3.1 定义

        直方图均衡化是一种简单有效的图像增强技术，通过改变图像的直方图来改变图像中各像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰。例如，过曝光图像的灰度级集中在高亮度范围内，而曝光不足将使图像灰度级集中在低亮度范围内。采用直方图均衡化，可以把原始图像的直方图变换为均匀分布（均衡）的形式，这样就增加了像素之间灰度值差别的动态范围，从而达到增强图像整体对比度的效果。

3.2 原理

        对在图像中像素个数多的灰度值（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并，从而增大对比度，使图像清晰，达到增强的目的。

        为了将原图像的亮度范围进行扩展， 需要一个映射函数， 将原图像的像素值均衡映射到新直方图中， 这个映射函数有两个条件：

        ①不能打乱原有的像素值大小顺序， 映射后亮、 暗的大小关系不能改变；

        ② 映射后必须在原有的范围内，即像素映射函数的值域应在0和255之间；

综合以上两个条件，累积分布函数是个好的选择，因为累积分布函数是单调增函数（控制大小关系），并且值域是0到1（控制越界问题），所以直方图均衡化中使用的是累积分布函数。

累积分布函数的数学原理：

        因为图像由一个个像素点组成，所以图像直方图均衡化是通过离散形式的累积分布函数求解的，直方图均衡化过程中，映射方法是：

        其中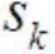，指当前灰度级经过累积分布函数映射后的值，n是图像中像素的总和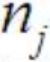，是当前灰度级的像素个数，L是图像中的灰度级总数。 

3.3 代码实现

灰度图像均衡化：

import cv2
import numpy as np
import matplotlib.pyplot as plt

img=cv2.imread('kid.jpg',1)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
equ = cv2.equalizeHist(img_gray)

plt.subplot(221), plt.imshow(img_gray, cmap=plt.cm.gray), plt.title('img_gray'), plt.axis('off')  # 坐标轴关闭
plt.subplot(222), plt.imshow(equ, cmap=plt.cm.gray), plt.title('equ'), plt.axis('off')  # 坐标轴关闭
plt.subplot(223), plt.hist(img_gray.ravel(), 256), plt.title('img_gray_hist')
plt.subplot(224), plt.hist(equ.ravel(), 256), plt.title('equ_hist')

plt.show()

cv2.waitKey(0)
cv2.destroyAllWindows()

  

 彩色图像均衡化：

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 彩色图像直方图均衡化
img = cv2.imread("kid.jpg", 1)

# 彩色图像均衡化,需要分解通道 对每一个通道均衡化
(b, g, r) = cv2.split(img)
bH = cv2.equalizeHist(b)
gH = cv2.equalizeHist(g)
rH = cv2.equalizeHist(r)
# 合并每一个通道
img_equ = cv2.merge((bH, gH, rH))

plt.subplot(221), plt.imshow(img), plt.title('img'), plt.axis('off')  # 坐标轴关闭
plt.subplot(222), plt.imshow(img_equ), plt.title('img_equ'), plt.axis('off')  # 坐标轴关闭
plt.subplot(223), plt.hist(img.ravel(), 256), plt.title('img_hist')
plt.subplot(224), plt.hist(img_equ.ravel(), 256), plt.title('equ_hist')

plt.show()

cv2.waitKey(0)
cv2.destroyAllWindows()

 

部分转自：https://www.jianshu.com/p/73e6ccbd8f3f