Towards Deep Learning Models Resistant to Adversarial Attacks(PGD adversarial training)
目录
- Introduction
-
- 内容简介
- An Optimization View on Adversarial Robustness
-
- 内容介绍
- Towards Universally Robust Networks
-
- The Landscape of Adversarial Examples
- Network Capacity and Adversarial Robustness
-
- 内容介绍
- Experiments: Adversarially Robust Deep Learning Models
-
- 内容介绍
- 个人感悟
Introduction
内容简介
主要介绍了本文的三个贡献，同时也是最关键的三个实验：
- 证明了为什么说PGD是最强的一阶攻击，是内部最大化问题的一个有效的解决方法。
- 对抗训练取得的分类边界相对于普通训练更加复杂，因此需要具有更大容量的网络结构，并通过实验验证了这一观点。
- 基于PGD解决内部最大化问题，以及选择大容量神经网络这两个观点，进一步设计实验证明了对抗训练的有效性。
An Optimization View on Adversarial Robustness
内容介绍
首先依据传统机器学习的观点，输入的图像数据 x x x与输出的分类向量 y y y服从于一个联合概率分布 D D D。则在损失函数给定的情况下，神经网络的训练过程是一个经验风险最小化（EMR）过程： min θ E ( x , y ) ∼ D [ L ( θ , x , y ) ] \min\limits_{\theta}E_{(x,y)\thicksim D}[L(\theta,x,y)] θminE(x,y)∼D[L(θ,x,y)]。即选择合适的参数 θ \theta θ，在 ( x , y ) (x,y) (x,y)遵循分布 D D D的前提下取得最小的期望损失。
而对抗训练是一个最大化最小化问题，本质上仍是一个期望风险最小化问题，不过是选择一组参数 θ \theta θ，使得当 x x x被添加了最强的干扰（即添加的干扰使得损失值最大）时，整体的期望风险依然最小。简单来说是寻找一个对最强对抗样本有最小期望风险的模型参数 θ \theta θ，即： min θ E ( x , y ) ∼ D [ max δ ∈ S L ( θ , x + δ , y ) ] \min\limits_{\theta}E_{(x,y)\thicksim D}[\max\limits_{\delta\in S} L(\theta,x+\delta,y)] θminE(x,y)∼D[δ∈SmaxL(θ,x+δ,y)]。
Towards Universally Robust Networks
The Landscape of Adversarial Examples
这里开始详细实验证明前面的贡献一，以说明为什么PGD是合理的内部最大化问题的求解方式。
第一组实验结果：
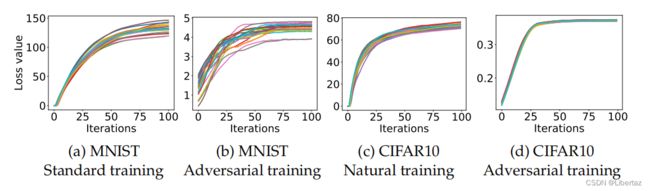首先以图一为例，图一面向一个特定的样本 x x x，横轴是PGD算法的迭代次数，纵轴是分类损失值，且同中有20条损失上升曲线，意味着对样本 x x x进行了20次随机重启的PGD攻击。实验对两个数据集进行，每个数据集在正常训练与对抗训练两种模型上进行实验，得出如下实验结论:
- 20次随机重启，随着迭代过程，损失值都上升到了一个基本相同的高度后趋于稳定，这意味着在干净样本 x x x周围有许多关于损失函数的局部最大值点。
- 在对抗训练的模型损失值上升的高度比正常训练模型的损失值上升的高度低很多。
基于以上两个结论，显然PGD算法合理地解决了内部最大化问题，因为确实找到了一个上限，且多次随机重启均无法突破这个上限。作者这里还进一步证明了随机重启的合理性，即将20次随机重启取得的20个对抗样本进行欧式距离与角度的比对，证明20次重启并非收敛到同一个极大值点，而是收敛到了20个不同的极大值点，这说明有许多个不同的局部极大值点，这表明这个上限是确实存在的，而不是因为多次随机重启最终殊途同归。此外实验结果2也初步表现了对抗训练的可行性。
第二组实验结果：
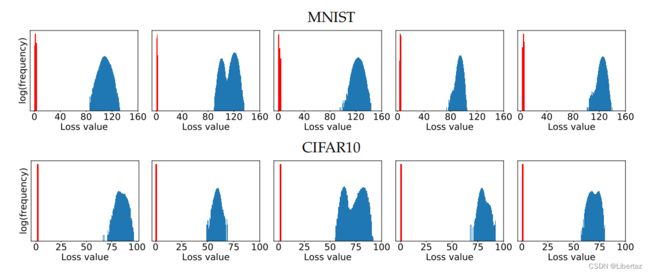每一张图片是对一个特定样本进行了 1 0 5 10^5 105次重启，分析每次重启后达到的极限值的分布规律，蓝色是在正常训练模型上进行实验，红色是在对抗训练模型上进行实验，显然，上限值均收敛于一定范围之内，这进一步证明了PGD算法解决局部最大化问题的有效性
Network Capacity and Adversarial Robustness
内容介绍
通过一组实验探究上述的第二个贡献：
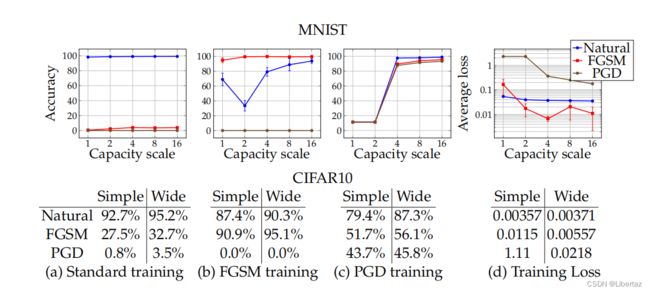在standard training的情况下对MNIST数据集而言，显然扩增模型容量可以小幅度改善防御效果，对Cifar10而言显然Wide网络对三种数据分类正确率都会有所进步。在FGSM training的情况下，MNIST数据集显然对原始样本的识别正确度略有下降，对FGSM的防御效果嘎嘎好，但对PGD攻击直接嗝屁，Cifar10数据集结论类似。而PGD training的情况下，显然在小容量的情况下MNIST数据集学习不到有效的内容，当模型容量增大时成功获得了优秀的分类与防御能力，对CIfar10数据集而言大的模型容量显然有更优秀的结果。
至此已经了解到，PGD对抗训练需要大的模型容量，且PGD确实是解决内部最大化问题的有效方式，同时SGD在解决外部最小化问题时同样适用，据此可以开展后续的一系列关于防御性能的评估实验。
Experiments: Adversarially Robust Deep Learning Models
内容介绍
首先，训练过程中的损失函数下降曲线告诉我们，对抗训练确实在有效进行：
后续对不同类型的攻击，进行了防御性能的测试。白盒攻击记为 A A A，基于完全相同的模型和训练方法得到的替代模型进行的黑盒攻击记为 A ′ A^{\prime} A′，基于完全相同的模型，但是并不了解训练策略，因此使用干净样本训练得到的替代模型进行的黑盒攻击记为 A n a t A_{nat} Anat，连模型都不知道的只能生成一个简单的替代模型的黑盒攻击记为 B B B。
在MNIST数据集上，训练时采用 40 × 0.01 ， 0.3 40\times0.01，0.3 40×0.01，0.3的对抗样本生成方式，测试时面对无穷范数为0.3的攻击：
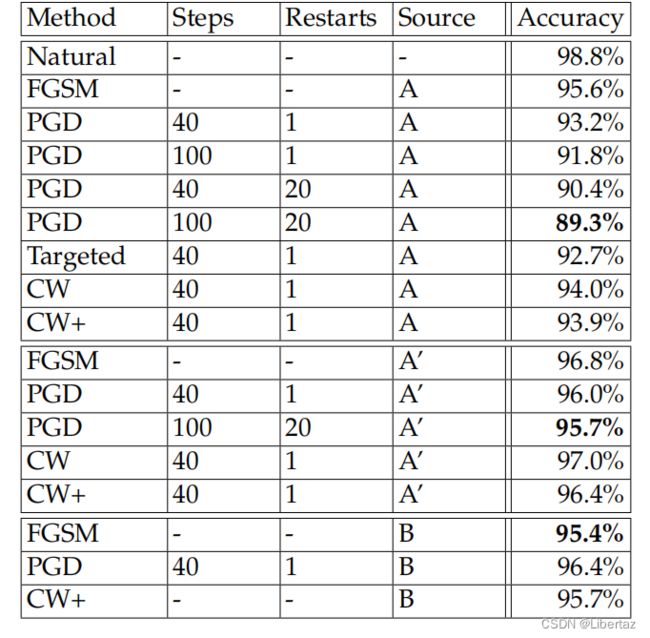
只能说MNIST数据集比较简单，训练集测试集相似度很高，所以防御效果很好，在测试集上有如此高的防御能力，没有较大的robustness gap（在训练集与测试集上的鲁棒性相差较大）。
在Cifar10数据集上，训练时采用 7 × 2 ， 8 7\times2，8 7×2，8的对抗样本生成方式，测试时面对 20 × 2 ， 8 20\times2，8 20×2，8的攻击：
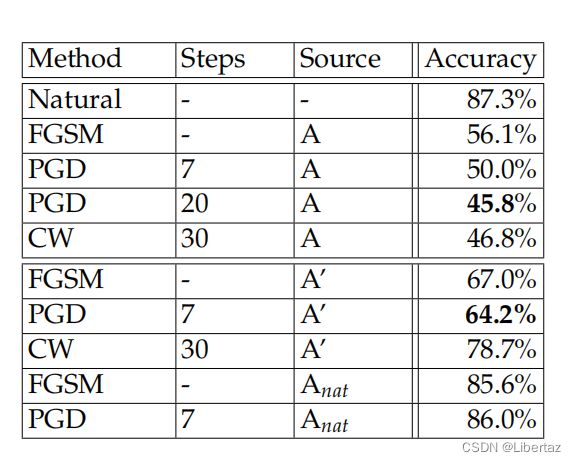
这里就体现了robusteness generalization的问题，原文没有给出在训练集上进行白盒攻击的效果，但是上面训练过程的损失值很低，可见在训练集上鲁棒性较好，但是在测试集对抗样本上上只有50%左右的防御力，说明鲁棒性泛化能力不太行。当然，与正常训练相比，这个防御能力还是好很多的。
最后由于PGD对抗训练基于无穷范数及固定的攻击参数，作者测试了在面对不同攻击参数及 l 2 l_{2} l2范数时的防御能力。
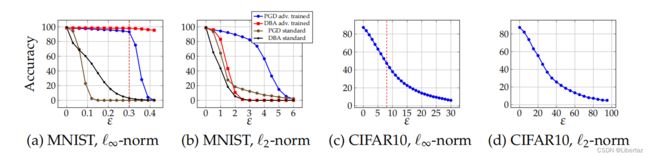在Cifar10数据上，显然，面对强度不断增强的攻击，明显防御性越来越差，在MNIST数据集上对比了PGD与DBA两种攻击方式在对抗训练与正常训练模型上的表现，如图所示。
个人感悟
-
总体就是测试PGD对抗训练的有效性，前期探索过程包括证明PGD是最强的与模型容量要大两组先验实验，前者通过多次重启均收敛及对收敛值的数据统计两个角度来验证，后者通过设计不同容量模型的对比试验来验证。后续实验验证了在面对不同类型攻击（白盒与各种黑盒），不同攻击算法，不同 ϵ \epsilon ϵ，不同约束条件下模型的防御性能，完成了最终的实验。实验设计很nice，很有参考性。
-
有没有一种可能，使用这种期望风险最小化公式可以提升对正常样本的识别概率？ min θ E ( x , y ) ∼ D [ max δ ∈ S L ( θ , x + δ , y ) + L ( θ , x , y ) ] \min\limits_{\theta}E_{(x,y)\thicksim D}[\max\limits_{\delta\in S} L(\theta,x+\delta,y)+L(\theta,x,y)] θminE(x,y)∼D[δ∈SmaxL(θ,x+δ,y)+L(θ,x,y)]（已经有了比如TRADES就类似）