多目标优化问题概述(基本模型和概念)
多目标优化问题(MOP)概述
1.数学模型
求解 MOP 的主要目的是:在给定的决策空间内,尽可能找到一系列满足问题约束条件的最优解集,为解决 MOP 的决策者提供相关数据。以最小化的 MOP 为例,其数学模型为:
m i n F ( x ) = ( f 1 ( x ) , f 2 ( x ) , ⋯ f m ( x ) ) T s . t x ∈ Ω ⊆ R n minF(x)=\left( f_1(x),f_2(x),\cdots f_m(x)\right)^T \\ s.t \,\,\,\,\,\,\,\,\,\,\,\,\,\,x\inΩ \subseteq ℛ^n minF(x)=(f1(x),f2(x),⋯fm(x))Ts.tx∈Ω⊆Rn
其中 x = ( x 1 , x 2 , . . . x n ) T {x=\left(x\mathop{{}}\nolimits_{{1}},x\mathop{{}}\nolimits_{{2}},...x\mathop{{}}\nolimits_{{n}} \left) \mathop{{}}\nolimits^{{T}}\right. \right. } x=(x1,x2,...xn)T是 n n n维决策空间的一个向量, m m m是目标函数的规模, Ω Ω Ω是决策空间( decision space ), f i ( x ) {f\mathop{{}}\nolimits_{{i}} \left( x \right) } fi(x)是多目标优化问题的目标函数。 F ( x ) : Ω → Θ ⊆ R m ( m ≫ 2 ) {F \left( x \left) : \Omega \xrightarrow {} \Theta \subseteq R\mathop{{}}\nolimits^{{m}} \left( m \gg 2 \right) \right. \right. } F(x):ΩΘ⊆Rm(m≫2)是将决策空间 Ω Ω Ω映射到 m m m 维目标空间(objective space ) Θ \Theta Θ 中的映射函数。
简单来说一个目标函数 F ( x ) F(x) F(x)包含多个目标子函数 f i ( x ) f_i(x) fi(x),实际求解目标函数是由求各子目标函数体现的,这正是与单目标优化问题的区别之处。
2. 一些概念介绍
- 支配(dominate)也译占优。
- 非支配解/Pareto最优解/非劣解:无法进行简单相互比较的解,不存在比它更优越解的解,也就是说该解体现了若干 f i ( x ) f_i(x) fi(x)的最优(不是所有 f i ( x ) f_i(x) fi(x)的最优)。
在单目标优化问题中,通常最优解只有一个,而且能用比较简单和常用的数学方法求出其最优解。然而在多目标优化问题中,各个目标之间相互制约,可能使得一个目标性能的改善往往是以损失其它目标性能为代价,不可能存在一个使所有目标性能都达到最优的解。 - Pareto集:一个MOP,对于一组给定的最优解集,如果这个集合中的解是相互非支配的,也即两两不是支配关系,那么则称这个解集为Pareto集(Pareto Set )。
即各Pareto最优解的集合。 - pareto排序:对当前种族非支配个体分配次序,然后移除再对非支配个体分配次序,对剩下的点重复以上定级过程,直到所有点都定级完成,也就是对整个种族进行等级排序。
3. 求解思想
在存在多个Pareto最优解的情况下,如果没有关于问题的更多的信息,那么很难选择哪个解更可取,因此所有的Pareto最优解都可以被认为是同等重要的。由此可知,对于多目标优化问题,最重要的任务是找到尽可能多的关于该优化问题的Pareto最优解。因而,在多目标优化中主要完成以下两个任务:
- 找到一组尽可能接近Pareto最优域的解。
- 找到一组尽可能不同的解。
第一个要求算法要保证可靠的收敛性,第二个要求算法保证充足的分布性(包括多样性和均匀性)。即要求求得尽可能均匀分布的pareto最优解集,然后根据不同的设计要求和意愿,从中选择最满意的设计结果。多目标优化问题最终获得的解实际是所有有效解中的一个解或确定全部非支配解。
4. 部分算法介绍
现有的多目标优化算法种类繁多,这里根据核心思想进行以下分类(选取部分):
| 核心思想 | 算法 |
|---|---|
| 基于Pareto支配关系 | NSGA,NSGAⅡ,GrEA,SDR |
| 基于维持算法多样性 | DMI,SDE,DIR |
| 基于聚合函数 | MOEA/D,DBEA-eps,NSGAⅢ |
| 基于指标(Indicator) | Hypervolume,HypE,R2 |
| 基于参考集 | TAA,Two-Arch2,TC-SEA |
- 进化算法(EA),遗传算法(GA)
该算法源自于解决单目标优化问题,也是后来解决多目标问题算法的发展基础了。在单目标优化问题中,传统的优化算法,如最速下降法、拟牛顿法、牛顿法、共轭梯度法等,通常需要函数的导数信息。然而在实际生活中,很多问题无法求出导数,因此,传统的优化方法就难以求出问题的全局最优解甚至是无法求出解。在这个背景下,进化算法(Evolutionary Algorithm)被提出,EA 是一种基于种群搜索的启发式算法,通过模仿生物进化来寻找最优解集。
GA是进化算法的一个分类,两者之间非常相似。它们的思想都是借鉴于生物学家达尔文所著《进化论》中的基本观点:适者生存、优胜劣汰的自然选择生物机理。其主要特点是以种群为基础,利用种群中个体之间的信息交流和特定自适应搜索策略寻找更适应环境的个体,非常适合处理极其复杂的非线性问题。
进化算法主要是对种群内的个体进行编码,然后利用繁殖机制产生后代模拟自然界中的生物进化,它不受问题本身的约束,不要求问题本身是否连续、可导、单峰还是多峰,也不要求问题本身是否离散还是连续(这就是启发式算法的魅力~)。进化算法能从 NP-Hard 问题中以概率的找到全局最优解。除此之外,由于种群中有多个个体,所以进化算法也可以设计成大规模并行算法。过程如下:
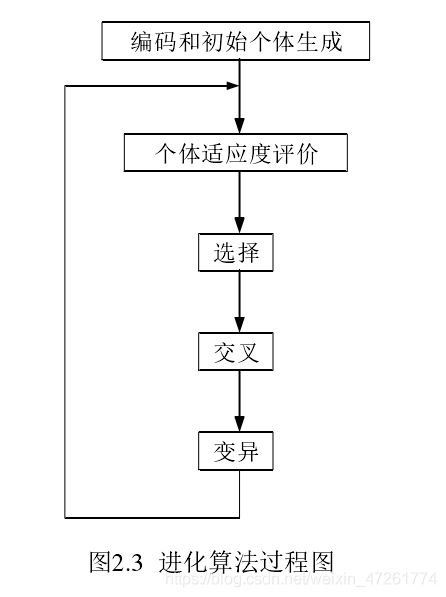
- NSGAⅡ算法
在众多多目标优化的遗传算法中,NSGAⅡ(Elitist Non-Dominated Sorting Genetic Algorithm)算法是影响最大和应用范围最广的一种多目标遗传算法。该算法主要优点如下三点:
① 提出了快速非支配的排序算法,降低了计算非支配序的复杂度,使得优化算法的复杂度由原来的 m N 3 mN^3 mN3降为 m N 2 mN^2 mN2。
②引入了精英策略,扩大了采样空间。将父代种群与其产生的子代种群组合在一起,共同通过竞争来产生下一代种群,这有利于是父代中的优良个体得以保持,保证那些优良的个体在进化过程中不被丢弃,从而提高优化结果的准确度。并且通过对种群所有个体分层存放,使得最佳个体不会丢失,能够迅速提高种群水平。
③引入拥挤度和拥挤度比较算子,这不但克服了NSGA算法中需要人为指定共享参数的缺陷,而且将拥挤度作为种群中个体之间的比较准则,使得准Pareto域中的种群个体能均匀扩展到整个Pareto域,从而保证了种群的多样性。
流程如下:
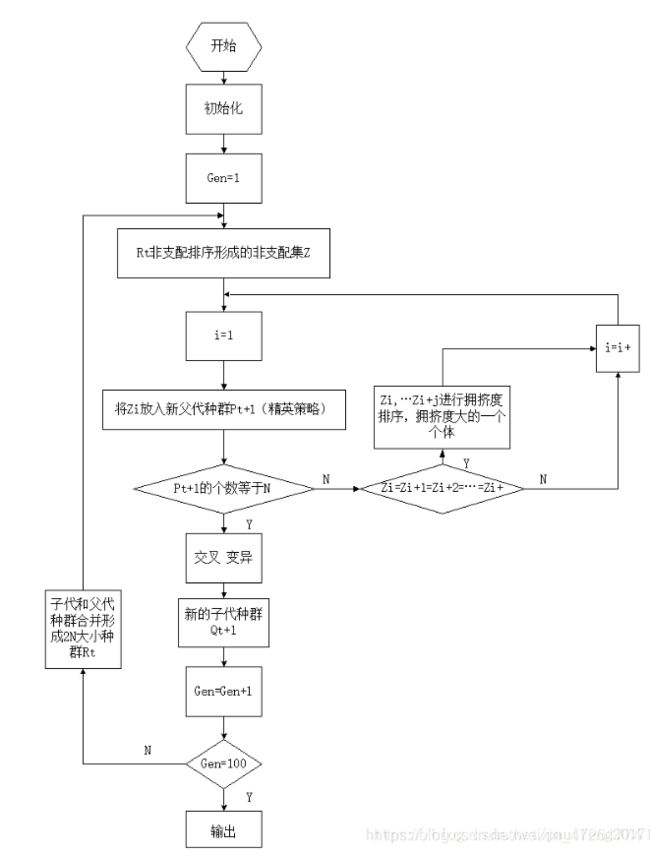
所谓基于Pareto支配关系,就是对当前获取点的优劣排序,以用于接下来 的淘汰和进化,不同的支配算法对此制定的规则不同,NSGAⅡ 是通过快速非支配排序算子对解集进行排序,然后利用个体拥挤度距离算子和精英策略选择算子进行进化。GrEA 算法基于网格,通过边界支配和边界差异增大算法的选择压力(选择压力影响点的进化方向,即影响最后的Pareto解),SDR是一种增强的支配关系,它在每一个定制的领域中保持一个收敛性最好的个体,平衡了算法的收敛性和多样性。
-
DMI算法,SDE算法,DIR算法
在研究多目标优化刚开始的时候,主要针对研究种群的收敛性,而很少考虑维持种群多样性(多样性很重要!!),所以产生了一些针对多样性的算法。DMI 机制根据种群的分布性决定是否激活维持种群多样性的策略。上文说的GrEA算法也引入网格排序、网格拥挤度和网格坐标距离等机制,以此来维持解的均匀性。SDE 算法通过比较邻居解与当前解的分布以及收敛的信息,决定如何移动其它解的位置,这个算法可以整合到NSGAⅡ框架中来形成完整的求解算法,DIR是一种指标,可以用来评估解集的多样性。
-
MOEA/D算法,DBEA-eps算法,NSGAⅢ算法
MOEA/D算法的思想就是“分解”,分解就是把多目标问题分成多个单目标子问题进行求解,那么怎么分呢?就要用到聚合函数,顾名思义,将多个单目标子指标聚合成一个大指标来衡量多目标问题。MOEA/D算法提出了3种聚合函数:权重求和(Weighted Sum)函数、切比雪夫(Tchebycheff )函数、边界交叉惩罚(penalty-based boundary intersection)函数。每一个子问题都会根据自己权重向量划分邻居,提高了邻居解的信息共享性,并且由于显而易见地降低了计算复杂性(把复杂多目标转成简单单目标,必须简单了啊)。值得一提,权重求和的考虑在多目标优化问题研究的开始就有提出(毕竟直觉上就可以这样处理),像RWGA,VEGA都是基于线性加权的多目标遗传算法,VEGA也算是开启多目标遗传算法研究的大门了。权重设置现如今有三种:固定权重,随机权重和适应性权方法,后两者方法用来更全面利用遗传算法的搜索功能。
在MEDA/D的框架上,又有很多改进算法被提出。DBEA-eps采用系统采样法产生参考向量,并且用 ε { \varepsilon } ε维持收敛性和多样性的平衡。NSGAⅢ基于参考点和非支配排序,首先将种群内个体的进行非支配排序,然后借助参考点集和归一化函数从最后一层非支配层选取个体进入下一代。NSGAⅢ 算法采用非支配排序策略增大算法的选择压力,通过参考点集将目标空间划分来维持种群的多样性。
-
Hypervolume,HypE,R2
指标可以用来评价一个多目标进化算法的好坏,主要从算法的收敛性能以及算法取得的最优解集在目标空间分布是否均匀两个方面来度量。比如反转世代距离(IGD)指标
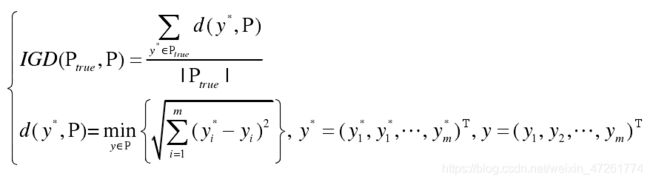
I G D IGD IGD指标其实就是计算算法求得最优Patero解集 P P P,与真实Patero解集 P t r u e P_{true} Ptrue的平均最小欧式距离( ∣ P t r u e ∣ |P_{true}| ∣Ptrue∣指 P t r u e P_{true} Ptrue元素个数)。 P t r u e P_{true} Ptrue也可以看作是从PF上均匀选取的参考点集。显然 I G D IGD IGD需要真实Patero解集,处理实际问题时有局限性。
那么利用指标,就可以指导点的进化过程。如超体积(Hypervolume)指标:
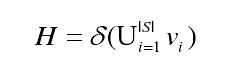
公式很简单,就是测量算法获得的非支配解集中各个体 i i i与参考点构成的超体体积。超体积 ( H V ) (HV) (HV)可以度量非支配解集所支配区域的尺寸大小,因此超体积越大,对应 I G D IGD IGD指标越小。理论证明,用 H V HV HV指标衡量解集的优劣性,一定能够找到真实 Pareto PF面。那么通过参考点,在保证超体积的同时,就可以完成对点的进化指导 。
H V HV HV不依赖真实的Pareto解集,适用于实际问题。但计算非常耗时,尤其是高维情况下。多目标超体积估值算法(HypE)就是针对解决这种情况的,利用蒙特卡罗算法来近似计算超体积的值,这样计算的代价要小很多并且也能得到近似值。除此之外,还有其它指标,如R2, Δ p { \Delta _p} Δp指标。另外,整合多种指标算子,将各个算子的优势集整合到一起能够更好的解决超多目标优化问题,如在二元指标算子的基础上引入参考点,使用二元指标算子维持算法的收敛性,使用参考点维持解集的多样性; I S D E + ISDE^+ ISDE+算子,其核心思想是将密度估计策略和目标函数值求和策略相结合。
- TAA算法,Two-Arch2算法,TC-SEA算法
参考点/集在算法中经常被使用到,与指标类似,可以用来评估种族的优劣,也可以用来调整种族进化过程。参考点可以是决策空间的,也可以是目标空间的。如真实PF上的取点,算法产生的非支配解,或由问题约束区间的取点等。目的不同,取法不同。双档案(TAA)算法,建立了两种档案:收敛性档案和多样性档案,收敛性档案用来保存每一代的非支配集,以维持算法的收敛性,多样性档案则用来维持算法的分布性。在此基础上改进的Two-Arch2算法,将收敛性档案的解集作为真实的参考集。在进化过程中,不仅可以把真实的 Pareto 解集作为参考集,而且也可以利用真实的参考集通过特定策略生成虚拟参考点集,这就是参考点集的选取。而TC-SEA其中使用的参考集生成策略是一边进化一边生成。
多目标优化问题研究到如今,提出的算法数不胜数,从不同角度可以有不同的分类。除了研究之初的几个基本算法,大部分算法都有着各种特征,所以单纯的分类其实并无太大意义,将这些特征拿出来揣摩揣摩或许可以更好的帮助理解,以及在纷扰繁多的算法中构建自己的认知体系。
5. 总结
以上只是对多目标优化问题及算法的普遍性介绍,随着研究的深入,更多基于此的算法和想法被提出来,如动态多目标优化(DMO),动态多目标优化问题的目标、自变量和参数均会随环境发生变化,因此算法除了需要优化多个彼此冲突的目标外,算法还要快速跟踪到变化了的 Pareto 前沿面(PF)或 Pareto 最优解集( PS)且产生分布性好的解;还有就是基于决策者的偏好的算法研究,这时目标不再是求得大量的非支配解,而是要根据决策者的偏好给出最终解。
从1967年,Rosenberg建议采用基于进化的搜索来处理多目标优化问题,到如今的各式各类基于进化算法的多目标算法蓬勃发展,实践已经表明了进化算法在处理多目标问题的有效性。因此想要学好多目标算法,首先理解进化算法是必要的。进化算法作为启发式算法,在多目标问题中应用如此之好,是否表明其他启发式算法也有如此好的效果,值得我去思考。
