【自然语言处理】【知识图谱】知识图谱表示学习(一):TransE、TransH、TransR、CTransR、TransD
【自然语言处理】【知识图谱】知识图谱表示学习(一):TransE、TransH、TransR、CTransR、TransD
【自然语言处理】【知识图谱】知识图谱表示学习(二):TranSparse、PTransE、TransA、KG2E、TransG
【自然语言处理】【知识图谱】知识图谱表示学习(三):SE、SME、LFM、RESCAL、HOLE
【自然语言处理】【知识图谱】知识图谱表示学习(四):【RotatE】基于复数空间关系旋转的知识图谱嵌入
【自然语言处理】【知识图谱】知识图谱表示学习(五):【PairRE】基于成对关系向量的知识图谱嵌入
一、简介
-
知识图谱及挑战
知识图谱以三元组的方式来描绘整个世界,大型知识图谱Freebase、DBpedia和YAGO等已经在各种应用程序中被广泛使用。但是,随着知识图谱规模的增加,面临着两个挑战:
-
数据稀疏
大型网络中节点太多而边太少。
-
计算低效
图谱尺寸增加,计算效率必然降低。
-
-
解决方案
为了解决上面的挑战,表示学习被引入至知识表示中。具体来说,就是将知识图谱中的实体和关系投影至低维连续空间中,从而获得一个分布式表示。相比于传统的one-hot表示,分布式表示的维度更低且计算复杂度也低。此外,通过低维向量间的距离计算还可以精准的展示实体间的相似性。
二、符号
- 使用 G = ( E , R , T ) G=(E,R,T) G=(E,R,T)来表示完整的知识图谱,其中 E = { e 1 , e 2 , … , e ∣ E ∣ } E=\{e_1,e_2,\dots,e_{|E|}\} E={e1,e2,…,e∣E∣}表示实体集合, R = { r 1 , r 2 , … , r ∣ R ∣ } R=\{r_1,r_2,\dots,r_{|R|}\} R={r1,r2,…,r∣R∣}表示关系集合, T T T表示三元组集合, ∣ E ∣ |E| ∣E∣和 ∣ R ∣ |R| ∣R∣表示实体和关系的数量。
- 知识图谱以三元组 ⟨ h , r , t ⟩ \langle h,r,t\rangle ⟨h,r,t⟩的形式表示,其中 h ∈ E h\in E h∈E表示头实体, t ∈ E t\in E t∈E表示尾实体, r ∈ R r\in R r∈R表示 h h h和 t t t间的关系。
三、TransE
1. 动机
-
将关系看作实体间的翻译
直觉上,将实体投影至低维向量空间时,具有相似语义的实体应该被投影至相同的簇,而含义不同的实体则属于不同的簇。例如 William Shakespeare \text{William Shakespeare} William Shakespeare和 Jane Austen \text{Jane Austen} Jane Austen应该投影至作者簇,而 Romeo and Juliet \text{Romeo and Juliet} Romeo and Juliet和 Pride and Prejudice \text{Pride and Prejudice} Pride and Prejudice则被投影至书籍簇中。它们之间的共同点就是共享相同的关系 works_written \text{works\_written} works_written,通过关系的翻译可以将作者和书籍投影至不同的簇。
-
word2vec \text{word2vec} word2vec的突破
word2vec \text{word2vec} word2vec通过上下文来学习词表示,得到的词向量存在一个有趣的现象:若两个词共现相似的语义或者句法关系,那么对应的词向量也相似。举例来说,
w ( k i n g ) − w ( m a n ) ≈ w ( q u e e n ) − w ( w o m a n ) \textbf{w}(king)-\textbf{w}(man)\approx \textbf{w}(queen)-\textbf{w}(woman) w(king)−w(man)≈w(queen)−w(woman)
上式表示在隐空间中king和man关系类似于queen和woman的关系。此外,除了在语义中发现这种近似关系,句法中也有类似关系,即
w ( b i g g e r ) − w ( b i g ) ≈ w ( s m a l l e r ) − w ( s m a l l ) \textbf{w}(bigger)-\textbf{w}(big)\approx\textbf{w}(smaller)-\textbf{w}(small) w(bigger)−w(big)≈w(smaller)−w(small) -
计算复杂度
首先,模型复杂度增加会导致高的计算代价和模型解释性差;
其次,复杂模型会过拟合;
最后,实验表明,具有相对较大关系量的知识图谱应用,简单模型和复杂模型表现相当;
因此,基于翻译的这种假设能够很好的平衡准确率和效率;
2. 方法
TransE \text{TransE} TransE会将实体和关系投影至低维向量空间 R d \mathbb{R}^d Rd,其中 d d d是嵌入向量维度的超参数。基于翻译的假设,对于每个三元组 ⟨ h , r , t ⟩ ∈ T \langle h,r,t \rangle \in T ⟨h,r,t⟩∈T,均期望嵌入向量和 h+r \textbf{h+r} h+r与尾实体嵌入向量 t \textbf{t} t接近。
具体来说, TransE \text{TransE} TransE会先定义一个评分函数
E ( h , r , t ) = ∥ h+r-t ∥ \mathcal{E}(h,r,t)=\parallel\textbf{h+r-t}\parallel E(h,r,t)=∥h+r-t∥
然后,基于该评分函数构建了一个基于边界的损失函数
L = ∑ ⟨ h , r , t ⟩ ∈ T ∑ ⟨ h ′ , r ′ , t ′ ⟩ ∈ T − m a x ( [ γ + E ( h , r , t ) − E ( h ′ , r ′ , t ′ ) ] , 0 ) \mathcal{L}=\sum_{\langle h,r,t\rangle\in T}\sum_{\langle h',r',t'\rangle \in T^-} max([\gamma+\mathcal{E}(h,r,t)-\mathcal{E}(h',r',t')],0) L=⟨h,r,t⟩∈T∑⟨h′,r′,t′⟩∈T−∑max([γ+E(h,r,t)−E(h′,r′,t′)],0)
其中, E ( h , r , t ) \mathcal{E}(h,r,t) E(h,r,t)是正样本的评分函数, E ( h ′ , r ′ , t ′ ) \mathcal{E}(h',r',t') E(h′,r′,t′)是负样本的评分函数, γ > 0 \gamma>0 γ>0是边界超参数, T − T^- T−是与 T T T对应的负样本三元组。简单分析该损失函数,其会最小化 E ( h , r , t ) \mathcal{E}(h,r,t) E(h,r,t)并最大化 E ( h ′ , r ′ , t ′ ) \mathcal{E}(h',r',t') E(h′,r′,t′),但是两者的差距不会大于 γ \gamma γ。
知识图谱中并没有显式的负样本三元组,因此按如下定义构造负样本三元组 T − T^- T−
T − = { ⟨ h ′ , r , t ⟩ ∣ h ′ ∈ E } ∪ { ⟨ h , r ′ , t ⟩ ∣ r ′ ∈ R } ∪ { ⟨ h , r , t ′ ⟩ ∣ t ′ ∈ E } , ⟨ h , r , t ⟩ ∈ T T^-=\{\langle h',r,t\rangle|h'\in E\}\cup\{\langle h,r',t\rangle|r'\in R\}\cup\{\langle h,r, t'\rangle|t'\in E\}, \langle h,r,t\rangle\in T T−={⟨h′,r,t⟩∣h′∈E}∪{⟨h,r′,t⟩∣r′∈R}∪{⟨h,r,t′⟩∣t′∈E},⟨h,r,t⟩∈T
上式的一个直观解释,随机使用其他三元组替换原始三元组 ⟨ h , r , t ⟩ \langle h,r,t\rangle ⟨h,r,t⟩的头实体、尾实体或者关系。此外,若生成的三元组已经在 T T T,那么就不会被加入 T − T^- T−。
-
知识补全
给定三元组中的任意两个元素,预测第3个元素被称为知识补全任务。该任务用于评估学习到的知识表示。
3. 缺点与挑战
TransE \text{TransE} TransE虽然简单有效,但是仍然存在一些缺点和挑战。
3.1 复杂关系
在知识补全任务中,给定三元组中的两个元素,可能会存在多个答案。例如,给定头实体 William Shakespeare \text{William Shakespeare} William Shakespeare和关系 works_written \text{works\_written} works_written,将会得到一个代表作的列表 Romeo and Juliet \text{Romeo and Juliet} Romeo and Juliet、 Hamlet \text{Hamlet} Hamlet和 A Midsummer Night’s Dream \text{A Midsummer Night's Dream} A Midsummer Night’s Dream。这些代表中共现相同的作者信息,但是在主题、背景、角色上不同。但是, TransE \text{TransE} TransE仅能为一个实体参数一个嵌入向量,这极大的限制了 TransE \text{TransE} TransE的能力。在许多文献中,将关系分为四类:1-to-1、1-to-Many、Many-to-1和Many-to-Many,而更加统计表明1-to-Many、Many-to-1和Many-to-Many类型的关系最多,但是 TransE \text{TransE} TransE仅能处理1-to-1的关系。
此外, TransE \text{TransE} TransE在处理自反关系时也存在困难。
3.2 一跳关系
TransE \text{TransE} TransE仅考虑了一条关系,忽略了长距离的隐关系。
3.3 效果和效率
TransE \text{TransE} TransE出于效率的原因,其函数和表示都被过度简化,导致其不足以建模知识图谱中的复杂实体和关系。如果评估效果和效率,仍然是非常大的挑战。
四、TransH
TransH \text{TransH} TransH主要是解决1-to-Many、Many-to-1和Many-to-Many问题的。
-
一个例子
在谈及国籍时, William Shakespeare \text{William Shakespeare} William Shakespeare应该和 Isaac Newton \text{Isaac Newton} Isaac Newton接近;而谈及职业时,则应该和 Mark Twain \text{Mark Twain} Mark Twain接近。
-
方法
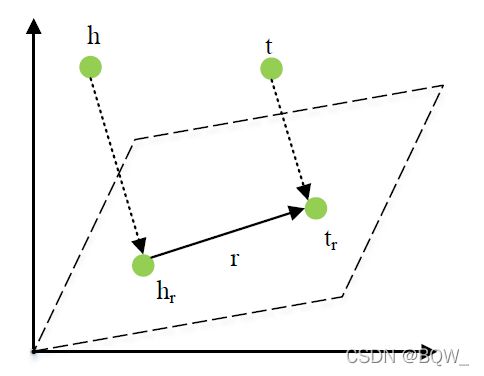
TransH \text{TransH} TransH通过为具有不同关系的相同实体赋予不同的向量表示来解决这个问题的。如上图所示, TransH \text{TransH} TransH为每个关系赋予一个超平面 w r \textbf{w}_r wr,然后判断超平面上的相似性,而不是原始的实体向量。给定三元组 ⟨ h , r , t ⟩ \langle h,r,t \rangle ⟨h,r,t⟩, TransH \text{TransH} TransH将会原始向量表示 h \textbf{h} h和 t \textbf{t} t投影至超平面 w r \textbf{w}_r wr上来获得投影向量 h ⊥ \textbf{h}_\perp h⊥和 t ⊥ \textbf{t}_\perp t⊥。翻译向量 r \textbf{r} r用于连接超平面 h ⊥ \textbf{h}_\perp h⊥和 t ⊥ \textbf{t}_\perp t⊥。评分函数定义为
E ( h , r , t ) = ∥ h ⊥ + r − t ⊥ ∥ \mathcal{E}(h,r,t)=\parallel\textbf{h}_\perp+\textbf{r}-\textbf{t}_\perp\parallel E(h,r,t)=∥h⊥+r−t⊥∥
其中,
h ⊥ = h − w r T h w r , t ⊥ = t − w r T t w r \textbf{h}_\perp=\textbf{h}-\textbf{w}_r^T\textbf{h}\textbf{w}_r,\quad \textbf{t}_\perp=\textbf{t}-\textbf{w}_r^T\textbf{t}\textbf{w}_r h⊥=h−wrThwr,t⊥=t−wrTtwr
其中, w r \textbf{w}_r wr是向量且约束 ∥ w r ∥ 2 \parallel\textbf{w}_r\parallel_2 ∥wr∥2为1。
-
训练
损失函数和训练方式同 TransE \text{TransE} TransE。
五、TransR
-
动机
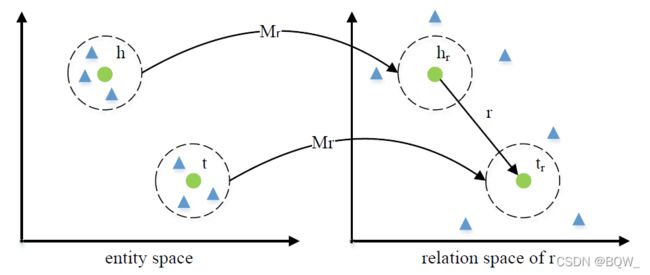
TransH \text{TransH} TransH通过使用超平面的方式为具有多个关系的实体赋予不同的向量表示,但是实体和关系仍然在相同的语义空间中,这限制了建模实体和关系的能力。 TransR \text{TransR} TransR假设实体和关系处于不同的语义空间中。
-
方法
如上图所示,三元组 ⟨ h , r , t ⟩ \langle h,r,t\rangle ⟨h,r,t⟩中 h,t ∈ R k \textbf{h,t}\in\mathbb{R}^k h,t∈Rk且 t ∈ R d \textbf{t}\in\mathbb{R}^d t∈Rd。 TransR \text{TransR} TransR首先会将 h \textbf{h} h和 t \textbf{t} t从实体空间投影至关系空间。也就是说,每个实体在每个关系上都有一个表示。 TransR \text{TransR} TransR的评分函数为
E ( h , r , t ) = ∥ h r + r − t r ∥ \mathcal{E}(h,r,t)=\parallel\textbf{h}_r+\textbf{r}-\textbf{t}_r\parallel E(h,r,t)=∥hr+r−tr∥
其中, h r \textbf{h}_r hr和 t r \textbf{t}_r tr是实体向量 h \textbf{h} h和 t \textbf{t} t在 r r r对应向量空间的表示,具体的投影过程为
h r = hM r , t r = tM r \textbf{h}_r=\textbf{hM}_r,\quad \textbf{t}_r=\textbf{tM}_r hr=hMr,tr=tMr
其中, M r ∈ R k × d \textbf{M}_r\in\mathbb{R}^{k\times d} Mr∈Rk×d是将实体映射至 r r r关系空间的投影矩阵。 TransR \text{TransR} TransR会约束嵌入向量的范数,具有 ∥ h ∥ 2 ≤ 1 \parallel\textbf{h}\parallel_2\leq 1 ∥h∥2≤1、 ∥ t ∥ 2 ≤ 1 \parallel\textbf{t}\parallel_2\leq 1 ∥t∥2≤1、 ∥ r ∥ 2 ≤ 1 \parallel\textbf{r}\parallel_2\leq 1 ∥r∥2≤1、 ∥ h r ∥ 2 ≤ 1 \parallel\textbf{h}_r\parallel_2\leq 1 ∥hr∥2≤1、 ∥ t r ∥ 2 ≤ 1 \parallel\textbf{t}_r\parallel_2\leq 1 ∥tr∥2≤1。
-
训练
TransR \text{TransR} TransR的训练方式同 TransE \text{TransE} TransE
六、CTransR
-
动机
知识图谱中的一些关系可以被划分为子关系,从而给出更加准确的信息。这些子关系间的不同,可以通过实体对来学习。举例来说,关系 location_contains \text{location\_contains} location_contains可以被认为包含子关系 city-street \text{city-street} city-street、 country-city \text{country-city} country-city、 country-university \text{country-university} country-university。随着考虑子关系,实体会被投影至语义向量空间中更加准确的位置。
-
方法
CTransR(Cluster-based TransR) \text{CTransR(Cluster-based TransR)} CTransR(Cluster-based TransR)可以看作是考虑子关系情况下的 TransR \text{TransR} TransR增强版本。具体来说,对于每个关系 r \text{r} r,所有的实体对 (h,t) \text{(h,t)} (h,t)会被聚类至若干个组。聚类主要是依据 t-h \textbf{t-h} t-h,其中 h \textbf{h} h和 t \textbf{t} t是通过 TransE \text{TransE} TransE预训练得到的。随后,通过每个聚类簇中的实体对可以学习到子关系向量 r c \textbf{r}_c rc,那么最终的评分函数
E ( h , r , t ) = ∥ h r + r c − t r ∥ + α ∥ r c − r ∥ \mathcal{E}(h,r,t)=\parallel \textbf{h}_r+\textbf{r}_c-\textbf{t}_r\parallel+\alpha\parallel\textbf{r}_c-\textbf{r}\parallel E(h,r,t)=∥hr+rc−tr∥+α∥rc−r∥
其中, ∥ r c − r ∥ \parallel\textbf{r}_c-\textbf{r}\parallel ∥rc−r∥是希望向量 r c \textbf{r}_c rc与 r \textbf{r} r的差距不要太大
七、TransD
-
动机
TransH \text{TransH} TransH和 TransR \text{TransR} TransR主要是解决不同关系的多实体表示问题,从而改善知识补全和三元组分类的效果。然而,这两个方法仅是根据关系来投影实体,忽略了实体的多样性。此外,使用矩阵-向量乘法实现投影操作将会导致高的时间复杂度,这导致在大规模图中的时间消耗太多。因此, TransD \text{TransD} TransD提出了一种基于实体和关系的动态映射矩阵,其能同时考虑实体和关系的多样性。
-
方法
TransD \text{TransD} TransD会为每个实体或者关系定义两个向量,一个是使用 TransE \text{TransE} TransE、 TransH \text{TransH} TransH和 TransR \text{TransR} TransR获得的原始向量,另一个是被用于构造投影句子的投影向量。
TransD \text{TransD} TransD使用 h,r,t \textbf{h,r,t} h,r,t表示原始向量, h p , t p , r p \textbf{h}_p,\textbf{t}_p,\textbf{r}_p hp,tp,rp来表示投影向量。使用两个矩阵 M r h , M r t ∈ R m × n \textbf{M}_{rh},\textbf{M}_{rt}\in\mathbb{R}^{m\times n} Mrh,Mrt∈Rm×n完成实体空间至关系空间的映射,这两个投影句子的动态计算为
M r h = r p h p ⊤ + I m × n M r t = r p t p ⊤ + I m × n \textbf{M}_{rh}=\textbf{r}_p\textbf{h}_p^\top+\textbf{I}_{m\times n}\quad \textbf{M}_{rt}=\textbf{r}_p\textbf{t}_p^\top+\textbf{I}_{m\times n} Mrh=rphp⊤+Im×nMrt=rptp⊤+Im×n
上式意味着实体和关系的投影向量被合并来决定最终的投影矩阵。评分函数定义为
E ( h , r , t ) = ∥ M r h h + r − M r t t ∥ \mathcal{E}(h,r,t)=\parallel\textbf{M}_{rh}\textbf{h}+\textbf{r}-\textbf{M}_{rt}\textbf{t}\parallel E(h,r,t)=∥Mrhh+r−Mrtt∥
投影矩阵被初始化为单位矩阵。
TransD \text{TransD} TransD提出了一种动态的方法来构造投影矩阵,从而能够同时考虑实体和关系的多样性,从而实现了更优的表述。此外,相较于 TransR \text{TransR} TransR,其具有更低的时间和空间复杂度。
引用文献
[1]. Zhiyuan Liu, Yankai Lin and Maosong SUn. Representation Learning for Natural Language Processing.