详解综合学习粒子群算法——CLPSO（附该文作者给出的matlab代码）

最近团队出了两篇基于CLPSO[1]的改进算法，这里根据自己的理解分析一下这个综合学习的算法，并将文章作者给出的源代码分享出来供大家学习：https://download.csdn.net/download/Bernard_S/12612817 (免费下载，本身就是从作者的主页搬的哈哈)。首先综合评价一下CLPSO，正如作者本人所言，该算法在单峰问题上结果非常好，但是处理单峰问题结果较差，我复写做的实验证明也确实如此，但是还是被该算法在多峰问题上的表现惊艳到了。所以目前大部分文章对其的改进都集中在提升开采能力以加强其在单峰问题上竞争力，接下来我就通过对CLPSO的详解来分析一下该算法在勘探与开采方面的表现以及简述一些已发表的论文对其的改进。（公式截图均来自参考文献）
简述粒子群算法
总所周知，粒子群算法赋予种群中每个粒子两个关键成分：速度与位置。并且迭代过程中通过这两个成分的变化来实现进化。具体方式如下：

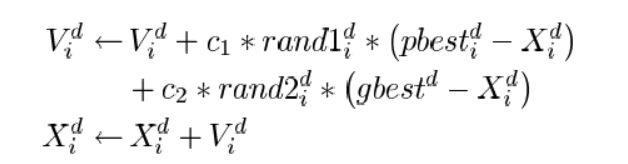
即每个粒子在进化中实际上由两个分量控制着方向，即本身的历史最优解与全局的历史最优解，实际上这两个分量也同时操控着粒子群算法的勘探与开采能力，自身最优拉动粒子在全局范围内勘探最优区域，而全局最优则拉动粒子向已有的最优区域移动以实现最优解的开采！
CLPSO的改进
以上简述实际上是为了方便这里分析CLPSO的改进是如何影响粒子群算法在勘探与开采之间的平衡，从而实现现在这种结果。实际上该算法改进十分简洁有效，接下来进行具体分析其综合学习策略。
其核心其实就是下面这一公式，该公式也仅仅是对经典的粒子群算法中速度更新项进行改进，将自身历史最优项换为新的综合学习因子同时将全局最优项删去。

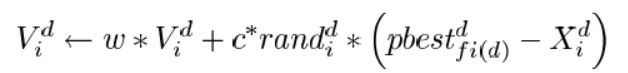
所以接下来我们重点分析一下他的综合学习因子。首先看看他如何产生：

for k=1:ps
    ar=randperm(D);
    ai(k,ar(1:m(k)))=1;
    fi1=ceil(ps*rand(1,D));
    fi2=ceil(ps*rand(1,D));
    fi=(pbestval(fi1)=pbestval(fi2))'.*fi2;
    bi=ceil(rand(1,D)-1+Pc(k));
    if bi==zeros(1,D),rc=randperm(D);bi(rc(1))=1;end
    f_pbest(k,:)=bi.*fi+(1-bi).*f_pbest(k,:);
end

简单描述就是：对每一个粒子，在整个种群中随机选取两个粒子，比较两个粒子适应度并取较优的一个作为待选，然后依据文章定义的交叉概率Pc来按维度将待选粒子与该粒子的历史最有进行交叉，以生成综合学习因子，即公式中的Pbest.fri。同时在迭代过程中记录粒子没有变化的迭代停滞次数（注意源代码中并未将变化的粒子停滞次数归零），当某个粒子的停滞次数大于阈值，则重新为其生成综合学习因子。
其Pc的定义如下

t=0:1/(ps-1):1;t=5.*t;
Pc=0.0+(0.5-0.0).*(exp(t)-exp(t(1)))./(exp(t(ps))-exp(t(1)));

也很容易理解，即对整个种群的每个粒子定义线性递增的Pc（Pc=[0,0.5]）且Pc不随迭代变化。
实际上整个算法所有的改进如上，十分的简单易懂却很有效，这里说说本人对其改进的理解：
首先为什么要去掉全局最优项？
实际上好多对CLPSO的改进会刻意将全局最优项加上以增强其开采能力，我认为其中HCLPSO[2]算是效果较好的变体，它主要就是将多种群拓扑引入，本身保留一个CL群然后生成一个新的带全局项的CL群，其实和众多该类改进一样，破坏了CLPSO本身的拓扑，所以实验证明在处理多峰问题时HCLPSO劣于CLPSO。说说我理解的为什么去掉全局最优项：首先，综合学习因子本身会选取随机两个粒子里面较好的一个，也就是说，全局最优在每次迭代中有不小的概率会被种群中的一个或多个粒子选择为学习目标。其次，全局最优项会大幅抵消综合学习因子的勘探能力（下文所述的振荡问题），因为本身综合学习因子是粒子自身最优与随机学习目标依概率的组合。
为什么综合学习因子会在多模态问题上起作用
原文中其实是有解释的，即粒子群算法本身进化中存在的振荡问题！从经典粒子群算法速度的进化公式来描述一下，我们可以看出，除了惯性项W*V，后面两项实际上控制了粒子整个进化过程的方向，也决定了粒子在搜索中对勘探与开采的侧重。那么当(Pbest-x）与（Gbest-x)这两项在多个维度中出去相互对立或者整体一致的方向时，其中的某一项必然失去作用甚至起到反作用，即力学中两个力同向，或完全反向。陷入多代这种进化的粒子必然会失去其搜索能力，不仅浪费计算次数，而且极易陷入早熟收敛。这就是为什么CLPSO在自身历史最优中混合入随机选取的目标，之后去掉全局最优，实际上就是避免了这一现象，事实证明效果显著！
最后将源代码贴上供大家学习，具体实验代码上文以附。

[1] J.J. Liang, A.K. Qin, P.N. Suganthan, S. Baskar, Comprehensive learning particle swarm optimizer for global optimization of multimodal functions, IEEE Trans. Evol. Comput. 10 (3) (2006) 281–295.

function [gbest,gbestval,fitcount]= CLPSO_new_func(fhd,Max_Gen,Max_FES,Particle_Number,Dimension,VRmin,VRmax,varargin)
%[gbest,gbestval,fitcount]= CLPSO_new_func('f8',3500,200000,30,30,-5.12,5.12)
rand('state',sum(100*clock));
me=Max_Gen;
ps=Particle_Number;
D=Dimension;
cc=[1 1];   %acceleration constants
t=0:1/(ps-1):1;t=5.*t;
Pc=0.0+(0.5-0.0).*(exp(t)-exp(t(1)))./(exp(t(ps))-exp(t(1)));
% Pc=0.5.*ones(1,ps);
m=0.*ones(ps,1);
iwt=0.9-(1:me)*(0.7/me);
% iwt=0.729-(1:me)*(0.0/me);
cc=[1.49445 1.49445];
if length(VRmin)==1
    VRmin=repmat(VRmin,1,D);
    VRmax=repmat(VRmax,1,D);
end
mv=0.2*(VRmax-VRmin);
VRmin=repmat(VRmin,ps,1);
VRmax=repmat(VRmax,ps,1);
Vmin=repmat(-mv,ps,1);
Vmax=-Vmin;
pos=VRmin+(VRmax-VRmin).*rand(ps,D);

for i=1:ps;
    e(i,1)=feval(fhd,pos(i,:),varargin{:});
end

fitcount=ps;
vel=Vmin+2.*Vmax.*rand(ps,D);%initialize the velocity of the particles
pbest=pos;
pbestval=e; %initialize the pbest and the pbest's fitness value
[gbestval,gbestid]=min(pbestval);
gbest=pbest(gbestid,:);%initialize the gbest and the gbest's fitness value
gbestrep=repmat(gbest,ps,1);

stay_num=zeros(ps,1);

ai=zeros(ps,D);
f_pbest=1:ps;f_pbest=repmat(f_pbest',1,D);
for k=1:ps
    ar=randperm(D);
    ai(k,ar(1:m(k)))=1;      %%%大家仔细看这里，看似作者希望加上全局最优项，实际上m并未更新，全局最优也一直没有使用
    fi1=ceil(ps*rand(1,D));
    fi2=ceil(ps*rand(1,D));
    fi=(pbestval(fi1)<pbestval(fi2))'.*fi1+(pbestval(fi1)>=pbestval(fi2))'.*fi2;
    bi=ceil(rand(1,D)-1+Pc(k));
    if bi==zeros(1,D),rc=randperm(D);bi(rc(1))=1;end
    f_pbest(k,:)=bi.*fi+(1-bi).*f_pbest(k,:);
end

stop_num=0;
i=1;


while i<=me&fitcount<=Max_FES
    i=i+1;
    for k=1:ps
        
        if stay_num(k)>=5
            %     if round(i/10)==i/10%|stay_num(k)>=5
            stay_num(k)=0;
            ai(k,:)=zeros(1,D);
            f_pbest(k,:)=k.*ones(1,D);
            ar=randperm(D);
            ai(k,ar(1:m(k)))=1;
            fi1=ceil(ps*rand(1,D));
            fi2=ceil(ps*rand(1,D));
            fi=(pbestval(fi1)<pbestval(fi2))'.*fi1+(pbestval(fi1)>=pbestval(fi2))'.*fi2;
            bi=ceil(rand(1,D)-1+Pc(k));
            if bi==zeros(1,D),rc=randperm(D);bi(rc(1))=1;end
            f_pbest(k,:)=bi.*fi+(1-bi).*f_pbest(k,:);
        end
        
        for dimcnt=1:D
            pbest_f(k,dimcnt)=pbest(f_pbest(k,dimcnt),dimcnt);
        end
        aa(k,:)=cc(1).*(1-ai(k,:)).*rand(1,D).*(pbest_f(k,:)-pos(k,:))+cc(2).*ai(k,:).*rand(1,D).*(gbestrep(k,:)-pos(k,:));%~~~~~~~~~~~~~~~~~~~~~~
        vel(k,:)=iwt(i).*vel(k,:)+aa(k,:);
        vel(k,:)=(vel(k,:)>mv).*mv+(vel(k,:)<=mv).*vel(k,:);
        vel(k,:)=(vel(k,:)<(-mv)).*(-mv)+(vel(k,:)>=(-mv)).*vel(k,:);
        pos(k,:)=pos(k,:)+vel(k,:);
        
        if (sum(pos(k,:)>VRmax(k,:))+sum(pos(k,:)<VRmin(k,:)))==0;
            e(k,1)=feval(fhd,pos(k,:),varargin{:});
            fitcount=fitcount+1;
            tmp=(pbestval(k)<=e(k));
            if tmp==1
                stay_num(k)=stay_num(k)+1;
            end
            temp=repmat(tmp,1,D);
            pbest(k,:)=temp.*pbest(k,:)+(1-temp).*pos(k,:);
            pbestval(k)=tmp.*pbestval(k)+(1-tmp).*e(k);%update the pbest
            if pbestval(k)<gbestval
                gbest=pbest(k,:);
                gbestval=pbestval(k);
                gbestrep=repmat(gbest,ps,1);%update the gbest
            end
        end
        
    end
    
    % if round(i/100)==i/100
    %     plot(pos(:,D-1),pos(:,D),'b*');hold on;
    %     for k=1:floor(D/2)
    %         plot(gbest(:,2*k-1),gbest(:,2*k),'r*');
    %     end
    %     hold off
    %     title(['PSO: ',num2str(i),' generations, Gbestval=',num2str(gbestval)]);
    %     axis([VRmin(1,D-1),VRmax(1,D-1),VRmin(1,D),VRmax(1,D)])
    %     drawnow
    % end
    
    if fitcount>=Max_FES
        break;
    end
    if (i==me)&(fitcount<Max_FES)
        i=i-1;
    end
end
gbestval