[PyTorch笔记]线性神经网络

1 学习路线

本篇文章将介绍神经网络的整个训练过程：

定义简单的神经网络架构
数据处理
如何训练模型。

2 线性神经网络

2.1 线性回归

回归是能为一个或多个自变量与因变量之间关系建模的一类方法。回归经常用来表示输入和输出之间的关系。在机器学习领域中的大多数任务都与预测有关，大多数会涉及到回归问题，但并不全是。

2.1.1 线性回归的基本元素

线性回归基于两个简单假设：

1.假设⾃变量$x$和因变量$y$之间的关系是线性的，即$y$可以表⽰为$x$中元素的加权和，这⾥通常允许包含观测值的⼀些噪声；
2.假设任何噪声都⽐较正常，如噪声遵循正态分布。

当我们的输⼊包含$d$个特征时，我们将预测结果$\hat{y}$ （通常使⽤“尖⻆”符号表⽰y的估计值）表⽰为：
$$\hat{y}=w_1{x}_1+...+w_d{x}_d+b.$$对于特征集合X，预测值$\hat{y}\in R^n$可以通过矩阵-向量乘法表⽰为：
$$\hat{y}=Xw+b.$$其中，X的每⼀⾏是⼀个样本，每⼀列是⼀种特征。$b$称为偏置（bias）、偏移量（offset）或截距（intercept）。偏置是指当所有特征都取值为0时，预测值应该为多少。这个过程中的求和将使⽤⼴播机制。给定训练数据特征X和对应的已知标签y，

线性回归的⽬标是找到⼀组权重向量$w$和偏置$b$：当给定从X的同分布中取样的新样本特征时，这组权重向量和偏置能够使得新样本预测标签的误差尽可能⼩。

在开始寻找最好的模型参数（model parameters）w和b之前，我们还需要两个东西：

（1）⼀种模型质量的度量⽅式；
（2）⼀种能够更新模型以提⾼模型预测质量的⽅法。

损失函数

损失函数（loss function）能够量化⽬标的实际值与预测值之间的差距。通常选择⾮负数作为损失，且数值越⼩表⽰损失越⼩，完美预测时的损失为0。最常用的损失函数为平方误差函数。当样本$i$的预测值为${\hat{y}}^{(i)}$，其相应的真实标签为$y^{(i)}$时，平⽅误差为：
$$l^{(i)}(w,b)=\frac{1}{2}({\hat{y}}^{(i)}-y^{(i)}{)}^2,$$在整个训练集$n$个样本上的损失均值为：
$$L(w,b)=\frac{1}{n}\sum _{i=1}^n{l}^{(i)}(w,b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}(w^T{x}^{(i)}+b-y^{(i)}{)}^2$$在训练模型时，我们希望寻找⼀组参数$（w^{\ast },b^{\ast }）$，这组参数能最⼩化在所有训练样本上的总损失$$w^{\ast },b^{\ast }=\underset{w,b}{\mathrm{argmin}}L(w,b).$$

解析解

解析解即可以用一个公式简单表达的线性回归的解。在线性回归问题中，我们的预测问题是最⼩化$\Vert y-Xw{\Vert }^2$。这在损失平⾯上只有⼀个临界点，这个临界点对应于整个区域的损失极⼩点。将损失关于$w$的导数设为0，得到解析解：$w^{\ast }=(X^{T}X{)}^{-1}{X}^{T}y.$

解析解可以进行很好的数学分析，但是它对问题的限制很严格，导致无法广泛应用在深度学习里。

随机梯度下降

梯度下降最简单的⽤法是计算损失函数（数据集中所有样本的损失均值）关于模型参数的导数（在这⾥也可以称为梯度）。但在每⼀次更新参数之前，我们必须遍历整个数据集，这样可能会导致实际执行过程非常耗时。因此，通常在每次计算更新时随机抽取一小批样本，这种变体叫做小批量随机梯度下降。

在每次迭代中，⾸先随机抽样⼀个⼩批量$B$，它是由固定数量的训练样本组成的。然后，计算⼩批量的平均损失关于模型参数的导数（也可以称为梯度）。最后，将梯度乘以⼀个预先确定的正数$\eta$，并从当前参数的值中减掉。

更新过程如下：

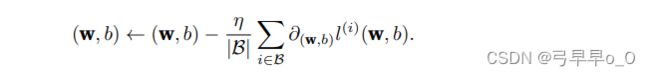
算法步骤：
（1）初始化模型参数的值，如随机初始化；
（2）从数据集中随机抽取⼩批量样本且在负梯度的⽅向上更新参数，并不断迭代这⼀步骤。
平方损失和放射变化的参数迭代如下:

用模型进行预测

给定特征估计目标的过程称为预测或推断。给定“已学习”的线性回归模型之后，就可以对实际问题中的某些变量进行预测。

2.1.2 正态分布与平方损失

正态分布和线性回归之间的关系很密切。首先，定义一个Python函数，计算正态分布。

import math
import numpy as np
def normal(x, mu, sigma):
	p = 1 / math.sqrt(2 * math.pi * sigma ** 2)
	return p * np.exp(-0.5 / sigma ** 2 * (x - mu) ** 2 )

可视化正态分布：

# 再次使⽤numpy进⾏可视化
x = np.arange(-7, 7, 0.01)
# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',
ylabel='p(x)', figsize=(4.5, 2.5),
legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])

均⽅误差损失函数（简称均⽅损失）可以⽤于线性回归的⼀个原因是：我们假设了观测中包含噪声，其中噪声服从正态分布。

2.1.3 线性回归的从0开始实现

import random
import torch
from d2l import torch as d2l


def synthetic_data(w,b,num_examples):
    """生成y=Xw+b+噪声"""
    X = torch.normal(0,1,(num_examples,len(w)))
    y = torch.matmul(X,w)+b
    y += torch.normal(0,0.01,y.shape)
    return X,y.reshape((-1,1))


# true_w = torch.tensor([2,-3,4]).float()
true_w = torch.tensor([2,-3,4],dtype=torch.float32)
true_b = 4.2
features, labels = synthetic_data(true_w,true_b,1000)
print('features:',features[0],'\nlabel:',labels[0])
# print(features.shape,labels.shape)
# torch.Size([1000, 3]) torch.Size([1000, 1]) 3个特征 1个标签 1000个样本
# 生成第二个特征
d2l.set_figsize()
d2l.plt.scatter(features[:,1].detach().numpy(),labels.detach().numpy(),1)
d2l.plt.show()

# 接受批量大小、特征矩阵、标签向量作为输入，生成大小为batch_size的小批量。
# 每个小批量包含一组特征和标签。
def date_iter(batch_size,features,labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定顺序
    random.shuffle(indices)
    for i in range(0,num_examples,batch_size):
        batch_indices = torch.tensor(
            indices[i:min(i+batch_size,num_examples)]
        )
        yield features[batch_indices],labels[batch_indices]

batch_size = 10
for X,y in date_iter(batch_size,features,labels):
    print(X,'\n',y)
    break

### 这个迭代器执行效率很低，在深度学习框架中实现的内置迭代器效率更高。
### 它可以处理存储在⽂件中的数据和数据流提供的数据。

# 初始化模型参数
'''
通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重，并将偏置初始化为0。
'''

w = torch.normal(0,0.01,size=(3,1),requires_grad=True)
b = torch.zeros(1,requires_grad=True)
# 自动微分计算梯度。


# 定义模型
def linreg(X,w,b):
    """线性回归模型"""
    return torch.matmul(X,w)+b

# 定义损失函数
def squared_loss(y_hat,y):
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

# 定义优化算法
# 朝着梯度下降的方向更新参数
# ⽤批量⼤⼩（batch_size）来规范化步⻓,
# 每一步更新的大小由学习率lr决定。
def sgd(params,lr,batch_size):
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()


# 训练
lr = 0.03
num_empochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_empochs):
    for X,y in date_iter(batch_size,features,labels):
        l = loss(net(X, w, b),y)  # X和y的小批量损失
        # 因为l形状是（batch_size,1），而不是一个标量。l中所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w,b],lr,batch_size) # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features,w,b),labels)
        print(f'epoch {epoch+1},loss {float(train_l.mean()):f}')


print(f"w的估计误差：{true_w-w.reshape(true_w.shape)}")
print(f"b的估计误差：{true_b-b}")

2.1.4 线性回归的简单实现

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2,-3],dtype=torch.float32)
true_b = 4.2
features,labels= d2l.synthetic_data(true_w,true_b,1000)

#读取数据集
def load_array(data_arrays,batch_size,is_train=True):
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset,batch_size,shuffle=is_train)

batch_size = 10
data_iter = load_array((features,labels),batch_size)

# 使用iter构造Python迭代器，并使用next从迭代器中获取第一项。
print(next(iter(data_iter)))


# 定义模型
'''
在PyTorch中，全连接层在Linear类中定义。
这里将两个参数传入nn.Linear中。
'''
# nn是神经网络的缩写
from torch import nn
net = nn.Sequential(nn.Linear(2,1))

# 初始化模型参数
# net[0]选择网络中的第一个图层，使用weight.data和bias.data两个方法访问参数
# 还可以用替换方法normal_和fill_来重写参数值
net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)

# 定义损失函数
loss = nn.MSELoss()

# 定义优化算法
# 指定优化参数：可通过net.parameters()从我们的模型中获得
trainer = torch.optim.SGD(net.parameters(),lr=0.03)

#训练
'''
在每个迭代周期⾥，我们将完整遍历⼀次数据集（train_data），不停地从中获取⼀个⼩批量的输
⼊和相应的标签。对于每⼀个⼩批量，我们会进⾏以下步骤:
• 通过调⽤net(X)⽣成预测并计算损失l（前向传播）。
• 通过进⾏反向传播来计算梯度。
• 通过调⽤优化器来更新模型参数。
为了更好的衡量训练效果，我们计算每个迭代周期后的损失，并打印它来监控训练过程。
'''
num_epochs = 3
for epoch in range(num_epochs):
    for X,y in data_iter:
        l = loss(net(X),y)
        trainer.zero_grad()
        l.backward()
        trainer.step()
    l = loss(net(features),labels)
    print(f'epoch {epoch+1},loss {l:f}')

# 计算误差
w = net[0].weight.data
print('w的估计误差：',true_w - w.reshape(true_w.shape))

b = net[0].bias.data
print('b的估计误差：',true_b - b)

2.2 Softmax回归

机器学习实践者⽤分类这个词来描述两个有微妙差别的问题：1. 我们只对样本的“硬性”类别感兴趣，即属于哪个类别；2. 我们希望得到“软性”类别，即得到属于每个类别的概率。这两者的界限往往很模糊。其中的⼀个原因是：即使我们只关⼼硬类别，我们仍然使⽤软类别的模型。

2.2.1 网络架构

对于任何具有d个输⼊和q个输出的全连接层，参数开销为O(dq)，这个数字在实践中可能⾼得令⼈望⽽却步。幸运的是，将d个输⼊转换为q个输出的成本可以减少到O(dq/n)，其中超参数n可以由我们灵活指定，以在实际应⽤中平衡参数节约和模型有效性 。

2.2.2 Softmax运算

Softmax回归的输出层是概率，要满足概率之和为1。可以将输出层$\widehat{y_j}$视为属于$j$类的概率。

2.2.3 损失函数

用对数似然函数。

2.2.4 信息论基础

信息论（information theory）涉及编码、解码、发送以及尽可能简洁地处理信息或数据。

信息量
表示信息不确定的程度。

2.2.5 Softmax回归的从0开始实现

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

# 初始化模型参数

num_inputs = 784
num_outputs = 10

w = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True, dtype=torch.float32)
b = torch.zeros(num_outputs, requires_grad=True)

# 定义Softmax操作
X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)


def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制


X = torch.normal(0, 1, (2, 5), dtype=torch.float32)
X_prob = softmax(X)
print(X_prob),
print(X_prob.sum(1))


# 定义模型
def net(X):
    return softmax(torch.matmul(X.reshape((-1, w.shape[0])), w) + b)


# 定义损失函数
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
print(y_hat[[0, 1], y])


def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])


print(cross_entropy(y_hat, y))


# 分类精度
def accuracy(y_hat, y):
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())


print(accuracy(y_hat, y) / len(y))


def evaluate_accuracy(net, data_iter): #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module):
        net.eval() # 将模型设置为评估模式
    metric = Accumulator(2) # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]
#分类正确的样本数/总样本数


class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]



# print(train_iter,test_iter)
# print(net)

# 训练

def train_epoch_ch3(net,train_iter,loss,updater):
    """训练模型一个迭代周期"""
    # 将模型设置为训练模式：
    if isinstance(net,torch.nn.Module):
        net.train()
    # 训练损失综总和，训练准确度综合、样本数
    metric = Accumulator(3)
    for X,y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat,y)
        if isinstance(updater,torch.optim.Optimizer):
            # 使用Pytorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()),accuracy(y_hat,y),y.numel())

    # 返回训练损失和训练精度
    return metric[0]/metric[2],metric[1]/metric[2]

class Animator:
    """在动画中绘制数据"""
    def __init__(self,xlabel=None,ylabel=None,legend=None,xlim=None,
                 ylim=None,xscale="linear",yscale="linear",
                 fmts=('-','m--','g-.','r:'),nrows=1,ncols=1,
                 figsize=(3.5,2.5)):
        # 增量地绘制多条线
        if legend is None:
            legend = []
        d2l.use_svg_display()
        self.fig,self.axes = d2l.plt.subplots(nrows,ncols,figsize=figsize)
        if nrows * ncols == 1:
            self.axes = [self.axes,]
        # 使用lambda函数捕获参数
        self.config_axes = lambda: d2l.set_axes(
            self.axes[0],xlabel,ylabel,xlim,ylim,xscale,yscale,legend)
        self.X,self.Y,self.fmts = None,None,fmts

    def add(self,x,y):
        """向图表中添加多个数据点"""
        if not hasattr(y,"__len__"):
            y = [y]

        n = len(y)
        if not hasattr(x,"__len__"):
            x= [x]*n
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]

        for i,(a,b) in enumerate(zip(x,y)):
            if a is not None and b is not  None:
                self.X[i].append(a)
                self.Y[i].append(b)
        self.axes[0].cla()
        for x,y, fmt in zip(self.X,self.Y,self.fmts):
            self.axes[0].plot(x,y,fmt)
        self.config_axes()
        display.display(self.fig)
        display.clear_output(wait=True)


def train_ch3(net,train_iter,test_iter,loss,num_epochs,updater):
    """训练模型"""
    animator = Animator(xlabel="epoch",xlim=[1,num_epochs],ylim=[0.3,0.9],
                        legend=['train loss','train acc','test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net,train_iter,loss,updater)
        test_acc = evaluate_accuracy(net,test_iter)
        animator.add(epoch+1,train_metrics+(test_acc,))
    train_loss,train_acc = train_metrics
    assert train_loss<0.5,train_loss
    assert train_acc <= 1 and train_acc>0.7,train_acc
    assert test_acc <= 1 and test_acc > 0.7,test_acc


lr = 0.1

def updater(batch_size):
    return d2l.sgd([w,b],lr,batch_size)


# 预测
def predict_ch3(net,test_iter,n=6):
    """预测标签"""
    for X,y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true + "\n" + pred for true,pred in zip(trues,preds)]
    d2l.show_images(
        X[0:n].reshape((n,28,28)),1,n,titles=titles[0:n]
    )
    d2l.plt.show()


if __name__ == '__main__':
    evaluate_accuracy(net, test_iter)
    predict_ch3(net,test_iter)
    num_epochs = 10
    train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

2.2.6 Softmax回归的简单实现

import torch
from torch import nn
from d2l import torch as d2l

batch_size = 256
train_iter,test_iter = d2l.load_data_fashion_mnist(batch_size)

"""PyTorch不会隐式调整输入的形状。
因此，在线性层前定义展平层（flatten），
来调整网络输入的形状"""
net = nn.Sequential(nn.Flatten(),nn.Linear(784,10))

def init_weight(m):
    if type(m) == nn.Linear:
        nn.init.normal(m.weight,std=0.01)

net.apply(init_weight)

# Softmax实现
loss = nn.CrossEntropyLoss(reduction="none")

# 优化算法
trainer = torch.optim.SGD(net.parameters(),lr=0.1)

# 训练

num_epochs = 10
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)
d2l.plt.show()