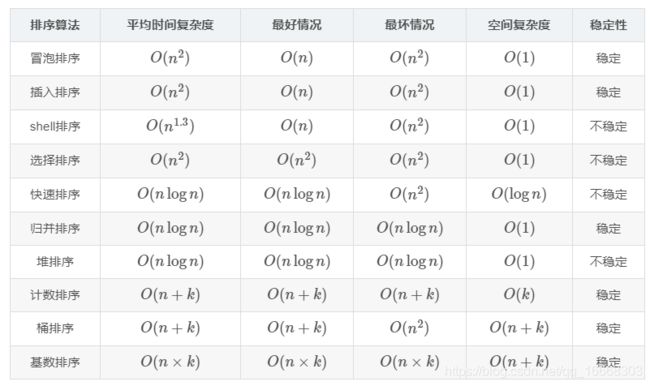
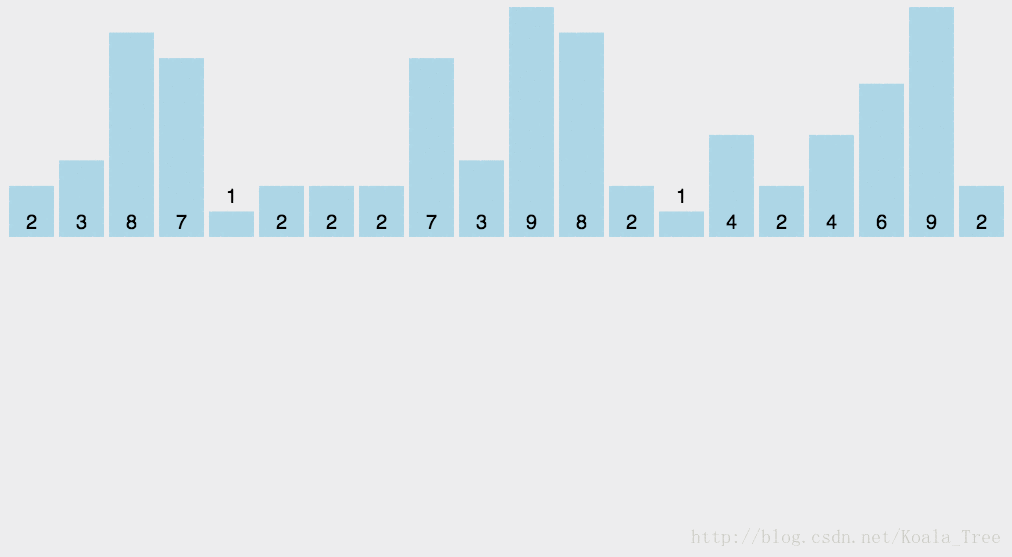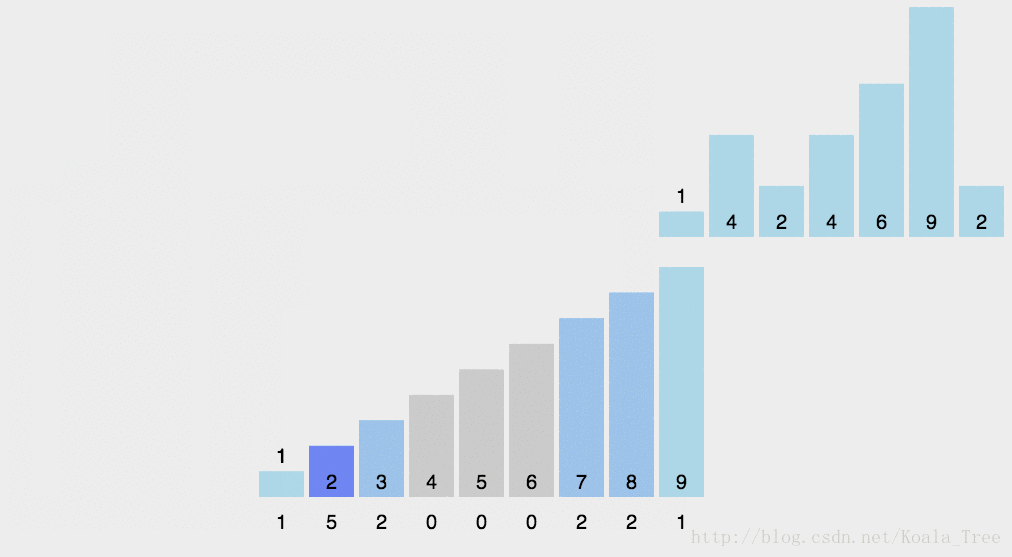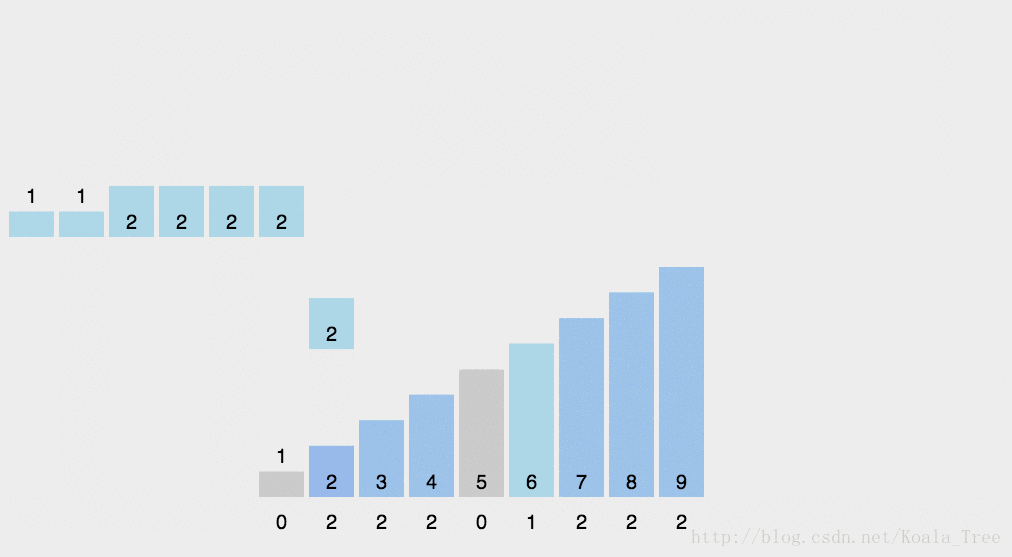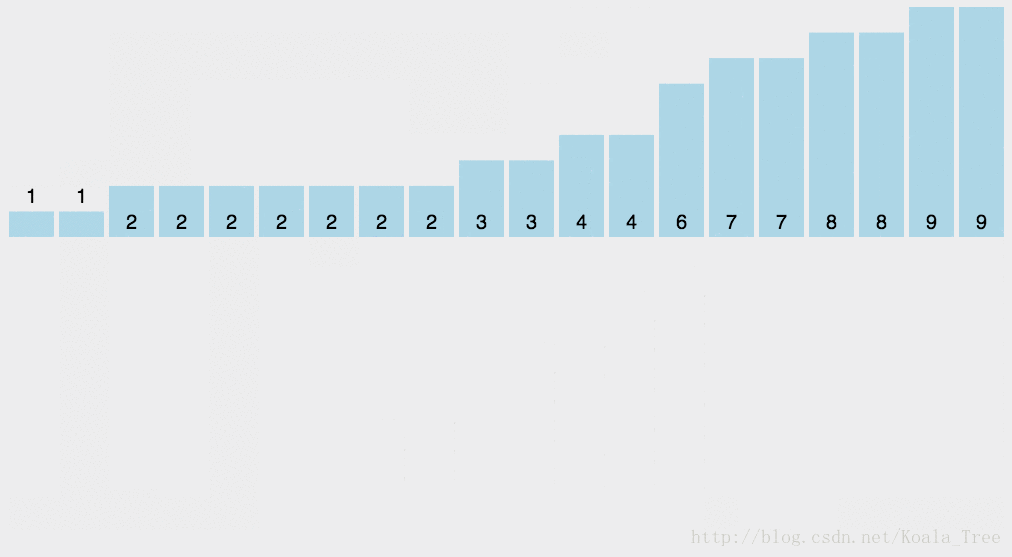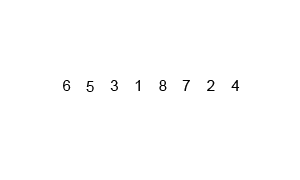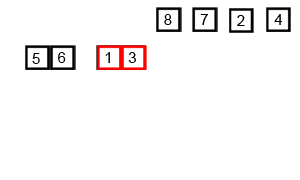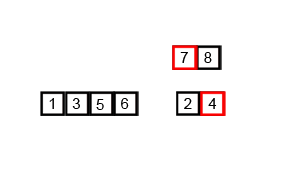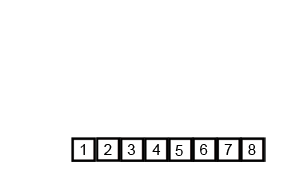C++实现经典排序算法
经典的排序算法是面试必备,数量掌握尤其重要。下面笔者将从算法思想、算法时间空间复杂度、算法实现、动图进行逐个展开,最后以表格总结
一、冒泡排序
1.1 基本思想
(1) 比较相邻的元素。如果第一个比第二个大,就交换;(冒泡策略)
(2) 对每一对相邻元素作(1)的步骤,从开始第一对到结尾的最后一对,这样在最右端元素就会是最大的数;
(3) 针对所有的元素重复以上的步骤,除了最后一个;
(4) 重复步骤1~3,直到排序完成。
1.2时空复杂度
平均时间复杂度:O(n2) ,设计到双重循环
空间复杂度:O(1)
1.3C++实现(常规实现)
//一次冒泡过程
template<class T>
//把a[0:n-1]中最大元素移到右边
void bubble(T a[],int n)
{
for(int i=0;i<n-1;i++)
{
if(a[i]>a[i+1])
{
swap(a[i],a[i+1]);
}
}
}
//冒泡排序
template<class T>
//对数组a[0:n-1]使用冒泡排序
void bubbleSort(T a[],int n)
{
for(int i=n;i>1;--i)
{
bubble(a,i);
}
}
1.3C++实现(优化+)
用空间换时间的方法就是存储isSwap标志,如果某次比较没有发生交换,即说明了已经有序,则无须进行遍历。
void BubbleSort(T a[], int n)
{
for (int i = 0; i < n - 1; i++)
{
bool isSwap = false; //先初始为不需交换
for (int j = 0; j < n - i - 1; j++)
{
if (a[j] > a[j + 1])
{
swap(a[j],a[j+1]);
isSwap = true;
}
}
//如果不需交换直接返回即可
if(!isSwap)
{
return;
}
}
}
1.3C++实现(优化++版)
(1)在优化版本的基础上再增添情况:已经遍历出部分有序的序列后,那部分也不用进行遍历,也就是说:发生交换的地方之后的地方不用遍历。
(2)使用current 和 last 来分别记录当前交换位置和最后一次交换位置,同样是空间换时间。
void bubbleSort(T a[], int n)
{ //记录位置,当前所在位置current和最后发生交换的地方last
int current;
int last = n - 1;
while(last > 0)
{
current = 0;
for(int i = 0;i<last;++i)
{
if(a[i] > a[i+1])
{
swap(a[i],a[i+1]);
//记录当前的位置,如果没有发生交换current值即for循环初始化的0
current = i;
}
}
//若current = 0即已经没有可以交换的元素了,即已经有序
last = current;
}
}
1.4 python实现
def bubbleSort(lists):
count = len(lists)
for i in range(0, count):
for j in range(i + 1, count):
if lists[i] > lists[j]:
lists[i], lists[j] = lists[j], lists[i]
return lists
1.5冒泡排序动图
二、选择排序
2.1 基本思想
(1) 初始状态:无序数组a[0:n-1]
(2) 首先找出最大(小)的元素,把它移动到a[n-1],然后在余下的n-1个元素中找到最大(小)的元素移到a[n-2],
(3) n-1趟结束,数组有序化。
2.2时空复杂度
平均时间复杂度:O(n2)
空间复杂度:O(1)
2.3C++实现(常规版)
template <class T>
//给数组a[0:n-1]的n个元素排序
void selectionSort(T a[],int n)
{
for(int size=n;size>1;size--)
{
int j=indexOfMax(a,size);
swap(a[j],a[size-1]);
}
}
//在a数组中,长度为n的情况下找到最大元素对应的索引号
int indexOfMax(T a[],int n)
{
int maxIndex=0;
for (int i=1;i<n;++i)
{
if(a[maxIndex]<a[i])
{
a[maxIndex]=a[i];
}
}
return maxIndex;
}
2.3C++实现(优化版+)
当我们引入一个变量来存储是否排序就可以及时终止,缩短时间
//及时终止的选择排序
template<class T>
void selectionSort(T a[],int n)
{
bool sorted=false;
for (int size=n;!sorted && (size>1);size--)
{
int maxIndex=0;
sorted=true;
//查找最大元素
for(int i=1;i<size;i++)
{
if(a[maxIndex]<=a[i])
{
maxIndex=i;
}
else
{//无序
sorted=false;
}
swap(a[maxIndex],a[size-1]);
}
}
}
## 2.4Python实现
```python
def selectionSort(list):
n=len(list)
for i in range (0,n):
min = i
for j in range(i+1,n):
if list[j]<list[min]:
min=j
if min != i:
list[min], list[i] = list[i], list[min]
return list
2.5 动态图
三、插入排序
3.1算法思想(抓扑克牌齐牌思想)
(1) 从第一个元素开始,该元素可以认为已经被排序;
(2) 取出下一个要排序的元素,在已经排序的元素序列中从后向前扫描;
(3) 如果该元素(已排序)大于新元素,将该元素移到下一位置;
(4) 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
(5) 将新元素插入到该位置后;
(6) 重复步骤2~5
3.2时空复杂度
平均时间复杂度:O(n2)
空间复杂度:O(1)
3.3C++实现
template<class T>
//在一个长度为n的有序数组a中插入一个x元素
void insert(T a[],int &n,const T& x)
{
int i;
for(i=n-1;i>=0&&x<a[i];--i)
{
a[i+1]=a[i];//往右边移动
}
a[i+1]=x;
n++;//多了个元素
}
//插入排序
template<class T>
//对长度为n的a数组进行排序
void insertionSort(T a[],int n)
{
for(int i=1;i<n;++i)
{
T t=a[i];
insert(a,i,t);
}
}
3.3C++实现另外一种插入排序
template <class T>
void insertionSort(T a[],int n)
{
for (int i=1;i<n;i++)
{//把a[i]插入到a[0,i-1]中
T t=a[i];
int j;
for( j=i-1;j>=0 && t<a[j];--j)
{
a[j+1]=a[j];//右移动
}
a[j+1]=t;
}
}
3.4 Python实现
def insertSort(lists):
for i in range(1, len(lists)):
key = lists[i]
j = i - 1
while j>=0 and lists[j]>key:
lists[j+1] = lists[j]
j = j - 1
lists[j+1] = key
return lists
3.5 动态图
四、堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
堆是具有以下性质的完全二叉树:
(1)每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;
(2)或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆,如图: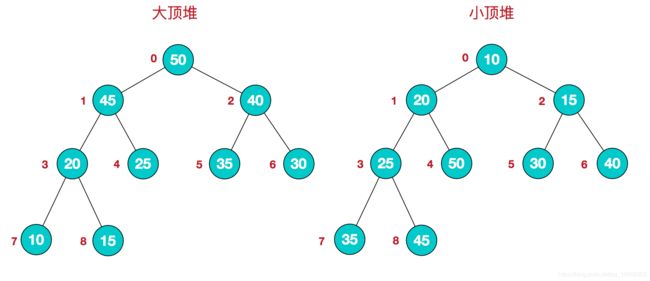
总结归纳公式:
(1)大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] (根节点>=左右子节点)
(2)小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] (根节点<=左右子节点)
4.1算法思想
(1) 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
(2) 将堆顶元素R1与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
(3) 由于交换后新的堆顶R1可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R1与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
4.2时空复杂度
平均时间复杂度:O(nlogn)
空间复杂度:O(nlogn)
4.3C++实现
void Heapify(int a[], int first, int end)
{
int father = first;
int son = father * 2 + 1;
while(son < end)
{
if(son + 1 < end && a[son] < a[son+1])
{
++son;
}
//如果父节点大于子节点则表示调整完毕
if(a[father] > a[son])
{
break;
}
else
{
//不然就交换父节点和子节点的元素
swap(a[father],a[son]);
//父和子节点变成下一个要比较的位置
father = son;
son = 2 * father + 1;
}
}
}
//堆排序
void HeapSort(int a[],int len)
{
int i;
//初始化堆,从最后一个父节点开始
for(i = len/2 - 1; i >= 0; --i)
{
Heapify(a,i,len);
}
//从堆中的取出最大的元素再调整堆
for(i = len - 1;i > 0;--i)
{
swap(a[i],a[0]);
//调整成堆
Heapify(a,0,i);
}
}
4.4动态图
五、计数排序
5.1算法思想
(1) 找出待排序的数组中最大和最小的元素;
(2) 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
(3) 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
(4) 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
5.2时空复杂度
平均时间复杂度:O(n+k)
空间复杂度:O(k)
5.3C++实现
template<class T>
//利用附加数组的计数排序a表示数组,n个数,r表示名次数组
void rearrange(T a[],int n,int r[])
{//使用附加数组u,将元素重排
T *u= new T [n];
//把a中元素移到u中正确位置
for(int i=0;i<n;i++)
{
u[r[i]]=a[i];
}
//把u中元素移回a
for(int i=0;i<n;i++)
{
a[i]=u[i];
}
delete [] u;
}
//名次计算,给a[0:n-1]的n个元素排名次
void rank(T a[],int n,int r[])
{ //初始化
for(int i=0;i<n;i++)
{
r[i]=0;
}
//比较所有元素对
for(int i=1;i<n;i++)
{
for(int j=0;j<i;j++)
{
if(a[j]<=a[i])
{
r[i]++;
}
else
{
r[j]++;
}
}
}
}
5.4 动态图
六、归并排序(分而治之算法的扩展)
6.1算法思想
分割:递归地把当前序列平均分割成两半。
集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
递归法(Top-down)
1.申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
2.设定两个指针,最初位置分别为两个已经排序序列的起始位置
3.比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到
4.重复步骤3直到某一指针到达序列尾
5.将另一序列剩下的所有元素直接复制到合并序列尾
迭代版
假设序列共有 {\displaystyle n} n个元素
1.将序列每相邻两个数字进行归并操作,则分成ceil(n/2)序列,则每序列有1or2个元素
2.若此时序列数不是1个则将上述序列再次归并,形成 ceil(n/4)}个序列,每个序列包含4/3个元素
3.重复步骤2,直到所有元素排序完毕,即序列数为1
6.2时空复杂度
平均时间复杂度:O(nlogn)
空间复杂度:O(n)
6.3C++实现(递归版本)
void merge(vector<int> &Array, int front, int mid, int end)
{
// 前提条件有四个:
// Array[front:mid]已经排序好
// Array[mid+1:end]已经排序好
// 拷贝Array[front:mid] to 左子数组
// 拷贝Array[mid+1:end] to 右子数组
vector<int> LeftSubArray(Array.begin() + front, Array.begin() + mid + 1);
vector<int> RightSubArray(Array.begin() + mid + 1, Array.begin() + end + 1);
int idxLeft = 0;
int idxRight = 0;
LeftSubArray.insert(LeftSubArray.end(), numeric_limits<int>::max());
RightSubArray.insert(RightSubArray.end(), numeric_limits<int>::max());
//选出LeftSubArray[idxLeft] 和 RightSubArray[idxRight]的最小值,然后将最小值放入Array[i]
for (int i = front; i <= end; i++)
{
if (LeftSubArray[idxLeft] < RightSubArray[idxRight])
{
Array[i] = LeftSubArray[idxLeft];
idxLeft++;
}
else
{
Array[i] = RightSubArray[idxRight];
idxRight++;
}
}
}
void mergeSort(vector<int> &Array, int front, int end)
{
if (front >= end)
return;
int mid = front + (end - front) / 2;
//分割
mergeSort(Array, front, mid);
mergeSort(Array, mid + 1, end);
//合并
merge(Array, front, mid, end);
}
6.3C++实现(迭代版本)
template<typename T>
void mergeSort(T arr[], int len)
{
T *a = arr;
T *b = new T[len];
for (int seg = 1; seg < len; seg += seg)
{
for (int start = 0; start < len; start += seg + seg)
{
int low = start, mid = min(start + seg, len), high = min(start + seg + seg, len);
int k = low;
int start1 = low, end1 = mid;
int start2 = mid, end2 = high;
while (start1 < end1 && start2 < end2)
b[k++] = a[start1] < a[start2] ? a[start1++] : a[start2++];
while (start1 < end1)
b[k++] = a[start1++];
while (start2 < end2)
b[k++] = a[start2++];
}
T *temp = a;
a = b;
b = temp;
}
if (a != arr)
{
for (int i = 0; i < len; i++)
{
b[i] = a[i];
}
b = a;
}
delete[] b;
}
6.4 动态图
七、快速排序(最难的排序)
快速排序使用分治法策略来把一个序列(list)分为较小和较大的2个子序列,然后递归地排序两个子序列。
7.1算法思想
1.挑选基准值:从数列中挑出一个元素,称为“基准”(pivot),
2.分割:重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(与基准值相等的数可以到任何一边)。在这个分割结束之后,对基准值的排序就已经完成,
3.递归排序子序列:递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。
7.2时空复杂度
平均时间复杂度:O(nlogn)
空间复杂度:O(logn)
7.3C++实现(递归版)
template <typename T>
void quickSortRecursive(T arr[], int start, int end)
{
if (start >= end)
return;
T mid = arr[end];//选划分元素为最后一个
int left = start;
int right = end - 1;
while (left < right)
{ //在整个范围内搜寻比枢纽元值小或大的元素,然后将左侧元素与右侧元素交换
//试图在左侧找到一个比枢纽元更大的元素
while (arr[left] < mid && left < right)
left++;
//试图在右侧找到一个比枢纽元更小的元素
while (arr[right] >= mid && left < right)
right--;
//交换元素
std::swap(arr[left], arr[right]);
}
if (arr[left] >= arr[end])
{
std::swap(arr[left], arr[end]);
}
else
{
left++;
}
quickSortRecursive(arr, start, left - 1);
quickSortRecursive(arr, left + 1, end);
}
template <typename T>
void quick_sort(T arr[], int len) {
quickSortRecursive(arr, 0, len - 1);
}