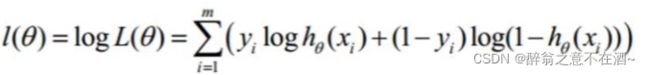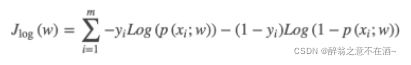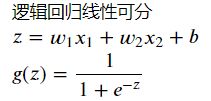机器学习-逻辑回归
一、什么是逻辑回归
二、Sigmoid函数
解释:将任意的输入映射到[0,1]区间我们在线性回归中得到一个预测值,再将该值映射到sigmoid函数中就完成了一个值到概率的转化,也就是分类任务。
其中z=![]() 。
。
实际上g(z)并不是预测结果,而是预测结果为正例的概率,一般来说阈值为0.5,也就是当g(z)>0.5,我们就说他是正例,g(z)<0.5就是负例,但在实际应用中也可能不同。比如我们预测一个人是否患有新型冠状病毒,我们这时如果只设置阈值为0.5,那么一个人患有新冠的概率为0.45,我们的模型也会认为他没有新冠,所以这时我们不妨把阈值设置的小一些如0.1,如果概率大于0.1你就要去做检查隔离,这样可以减少误差防止漏放病人。
上述可知:
P(y=0|w,x) = 1 – g(z) #预测为负例
P(y=1|w,x) = g(z) #预测为正例
那么我们可以得到函数表达式:
P(正确) =![]() *
* ![]()
![]() 为某一条样本的预测值,取值为0或者1.
为某一条样本的预测值,取值为0或者1.
三、极大似然估计
公式:g(z) = ![]()
因此我们要去寻找一个w的值使得g(z)正确的概率最大,而我们在上面的推理过程中已经得到每个单条样本预测正确概率的公式:
P(正确) =![]() *
* ![]()
若想让预测出的结果全部正确的概率最大,根据最大似然估计,也就是所有样本预测正确的概率相乘得到的P(总体正确)最大,似然函数如下:
我么对其取对数可得:
得到的这个函数越大,证明我们得到的W就越好.此时为梯度上升求最大值,引入j(θ)=(-1/m)L(θ)转化为梯度下降任务,得到公式如下:
这就是其代价函数,也称交叉熵函数。
四、求解W
我们对代价函数求导可得:
然后采用梯度下降来更新w:
五、代码解释
1、创建数据并进行切割
# data数据 4,3 x1, x2, y
data = np.array([
[1, 1, 0],
[1, 2, 0],
[0, 0, 1],
[-1, 0, 1]
])
#数据集切分, 前两列特征,最后一列作为标签
x = data[:, :-1]
y = data[:, -1:]
print(x)
print(y)2、调用模型LogisticRegression()训练预测
model = LogisticRegression()
model.fit(x, y.ravel())
y_ = model.predict(x)
print(y_)3、打印输出的可能性, 第一列为0样本,第二列为1样本
print(model.predict_proba(x))w = model.coef_
b = model.intercept_
print(w)
print(b)