阅读笔记Neural Ordinary Differential Equations
在残差网络中有下面的形式:
h t + 1 = h t + f ( h t , θ t ) (1) \mathbf h_{t+1} = \mathbf h_{t} + f(\mathbf h_{t}, \theta_t) \tag{1} ht+1=ht+f(ht,θt)(1)
连续的动态系统通常可以用常微分方程(ordinary differential equation, ODE)表示为:
d h ( t ) d t = f ( h ( t ) , t , θ ) (2) \frac{d\mathbf h(t)}{dt} = f(\mathbf h(t), t, \theta) \tag{2} dtdh(t)=f(h(t),t,θ)(2)如果动态系统中的 f f f用神经网络的模块表示,就得到了神经常微分方程,公式(1)可以看做是公式(2)的欧拉离散化(Euler discretization)。
输入是 h ( 0 ) \mathbf h(0) h(0),输出是 h ( T ) \mathbf h(T) h(T),也就是常微分方程初值问题在T时刻的解。
下图所示是残差网络和神经常微分方程的区别。纵轴代表 t t t,残差网络的状态变化是离散的,在整数位置计算状态的值,而神经常微分方程的状态是连续变化的,计算状态值的位置由求解常微分方程的算法决定。
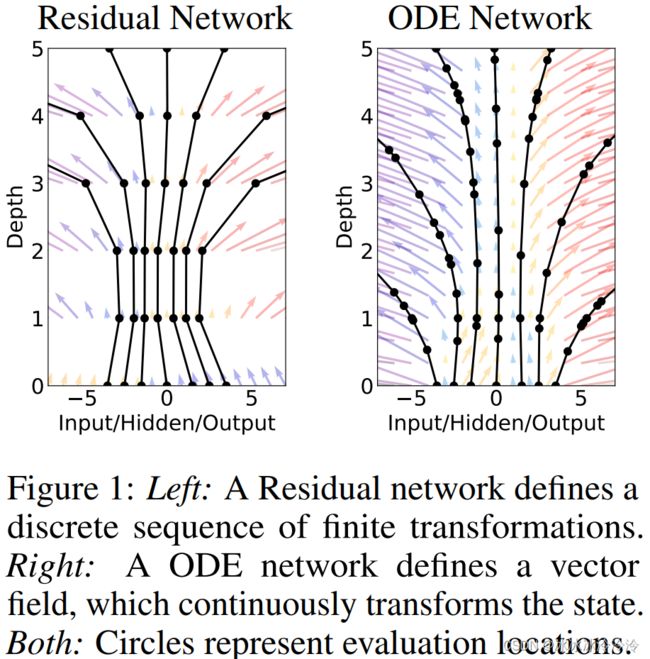
神经常微分方程就是用神经网络模块来表示常微分方程里的 f f f,同时神经常微分方程又可以作为一个模块嵌入大的神经网络中。
参数的优化
普通的常微分方程中的参数 θ \theta θ是固定的,但是神经常微分方程是神经网络的参数,所以需要优化。神经网络的参数用反向传播进行优化,神经常微分方程作为神经网络的一个模块,也需要支持反向传播,需要求损失函数关于 z ( t 0 ) , t 0 , t 1 , θ \mathbf z(t_0), t_0, t_1, \theta z(t0),t0,t1,θ的梯度。因为不只需要优化神经常微分方程中的参数,要需要优化神经常微分方程之前的模块的参数。
直接对积分的前向过程做反向传播理论上是可行的,但是需要大量的内存并导致额外的数值误差。
为了解决这些问题,论文提出使用adjoint法来求梯度。adjoint法可以通过求解另一个ODE来计算反传时需要的梯度。
考虑优化一个标量损失函数,这个损失函数的输入是ODE的输出。

定义adjoint为 a ( t ) = − ∂ L ∂ z ( t ) a(t)=-\frac{\partial L}{\partial \mathbf z(t)} a(t)=−∂z(t)∂L。
adjoint满足ODE:
d a ( t ) d t = − a ( t ) ⊤ ∂ f ( z ( t ) , t , θ ) ∂ z \frac{da(t)}{dt} = -a(t)^\top \frac{\partial f(\mathbf z(t), t, \theta)}{\partial \mathbf z} dtda(t)=−a(t)⊤∂z∂f(z(t),t,θ)论文在附录中给出了证明。
损失函数关于 z ( t 0 ) , t 0 , t 1 , θ \mathbf z(t_0), t_0, t_1, \theta z(t0),t0,t1,θ的梯度都可以通过求解ODE得到。