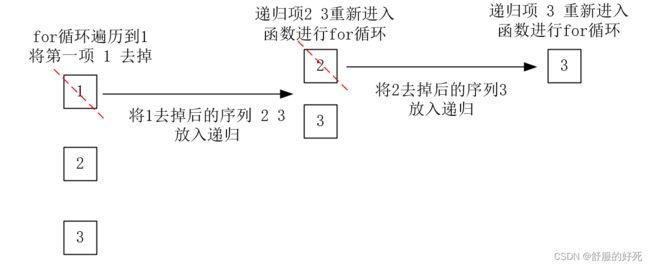
行列式求值

粘贴个行列式求值方法

求行列式的值时，所需项的序列号，但是会有零。

function [t,m,p,g] = hls1(t,m,p,g)   
% 举例使用 [a,b,c,r] = hls1([1:3],[],0,[]);
% 后加的注释，具体给忘了，注释可能有错
%生成行列式计算中每一项对应不同重复行号的序列值。
% 但是只保留交换位置部分，导致出现较多空值。
% 其中 t 应该为 行列式的行/列号n(方阵一样) ，但是为了编程找序列号方便，改成输入为1：n的矩阵
gz=g;%用来保存上次迭代后的序列值
    for i = 1:numel(t) %遍历矩阵t的每一项
            m=[m t(i)];%将t中的每一项进行叠加
            tt=t;%将矩阵t 赋给 tt。 因为在对每一项对所应序列值每次叠加一个项时
            t(find(t==t(i))) = []; %都会通过本步骤将该项进行清除，
            [t,m,p,g] = hls1(t,m,p,g);%这里的矩阵t是清除第一项后的，将剩下的项继续递归。
            % 即矩阵1 2 3 4 ，在1 的for循环中清楚1，并对剩下的2 3 4 继续for循环单个清除，余下递归  
            t =tt;%将矩阵tt重新赋给t,因为上述递归后，t就为空了
            if numel(m)>=1 %只将每一项中的序列中有值个数大为1的进行保留 
                 %不然由于每次for循环是1：t,如果t=4 就是4*4*4，如果筛选一波就是4*3*2
                p=p+1;% 序列值个数累计值 即t!个项  一项对应一个序列值
                g= zeros(p,p); %不初始化g值会赋值失败
                g =gz;%将上述所保留的g矩阵 重新 赋给g矩阵
                g(p,1:numel(m)) = m; %将当前的序列值 给存储在序列矩阵中的第p项
                gz = g; %将当前序列值存储在矩阵序列矩阵中
%                 m
            end
            m=[];%初始化每一项所对应的序列。
    end
end

粘个上步的逻辑图

对项的序列号中的零值去除

function [T] = gs(n)
% 举例使用 [T] = gs(3)
% 对序列矩阵中的零值进行清除
[a,b,c,r] = hls1([1:n],[],0,[]);%获取带有0值的序列矩阵
[g,s] = size(r); % 获取序列矩阵大小（行列值）
T = r;% 给r换个名
    for i =2:g %第一个不存在0 所以从2开始
        z = numel(find(T(i,:)==0)); % 选择序列矩阵中，当前行所存在的零值个数
        if z~=0 % 如果零值个数不为0
        T(i,:) =[  T(i,((n-z)+1):end) T(i,1:(n-z)) ]; %则将有值部分和无值部分进行颠倒
        end
        temp1 = T(i-1,:);%进而，为了将上述有值部分，用于下部分的补齐，则获取上一行序列值
        temp = T(i,:);% 获取当前行序列值
        temp(find(T(i,:)==0)) = temp1(find(T(i,:)==0));
        %将上一行中与当前行中为0值位置的值，赋予给当前行中属于零位置的值
        % 用temp 和temp1是因为 不赋值没办法用find进行索引
        T(i,:) = temp;%在换回去
    end
end

找到每一项的逆序数

function [temp,p] = nx(temp,p)
% 找到一行数据（一维数据）中的逆序数值
    if numel(temp)>=1% 当矩阵内值的个数大于等于1时，作为最终的截至条件
        for i=1:numel(temp) % 遍历一维数据
            if temp(1)>temp(i) % 如果一维度数据中的第一个数据 大于 之后的数据
                p=p+1;    % 则逆序数加1
            end  
        end
        temp(1)=[];  % 去掉一维数据中第一个数据，形成新的一维数据
        [temp,p] = nx(temp,p); %并将新的一维数据，和当前累加的逆序数值放入递归，对新一维数据求取逆序数
    end
end

计算所有项中的逆序数

function[ a,z] =nxs(a,z)
% 提取所有序列中的逆序数值
    if numel(a) > 0 % 当矩阵中不存在序列时，停止递归
        [x,y] = nx( a(1,:),0);  %获取矩阵中第一行序列的逆序数值 y
        a(1,:)=[]; % 去除矩阵中第一行序列，形成新的矩阵
        z=[z;y]; % 将矩阵中第一行序列的逆序数值保存在z中，进行记录
        [a,z] = nxs(a,z);%将对新矩阵不断递归，并将矩阵中第一行序列的z值进行不断的递归保存
    end
end

计算行列式的值

function [last] = xh(jz)
% 求行列式的值 jz为行列式
% a为行列式的序列矩阵
[pt1,pt2] = size(jz);%jz为方阵，获取其行/列值
a = gs(pt1);%生成序列矩阵a
[p,n] = size(a);
[x,y] = nxs(a,[]);%获取行列式的序列矩阵a 每一行对应的逆序数矩阵 y
mo = mod(y,2);%如果逆序数为1则判为奇序列，如果逆序数为0 则判为偶序列
last =0; %初始化行列式的值
    for i =1:p %遍历序列矩阵a中的每一行
        at = a(i,:); %获取序列矩阵的每一行用于求取该行对应项的值
        ma=1; % 初始化每一行中该行对应项的值
            for j=1:n  % 遍历 每一行中所有元素(下标)对应的值
                ma = jz(j,at(j))*ma; %将 每一行中所有元素(下标)对应的值相乘
            end
            if mo(i,1) ~=0
                ma = -ma; %如果每一行对应项的值为奇序列则做减法
            end
        last = ma+last; %累加每一行对应项的值
    end
end

示例

clear
clc
n=3;
magic(n)
xh(magic(n))
det(magic(n))

粘个结果