deepLearning-One hidden layer Neural Network一个隐藏层的神经网络

一直是跟着cousera上吴恩达的课学下来的，目前到一课程第四周，还没做第四周作业。

除了明显为个人手写并用手机拍摄，以下提供的图片都来自吴恩达老师课件的截图

献上关键理解图一张

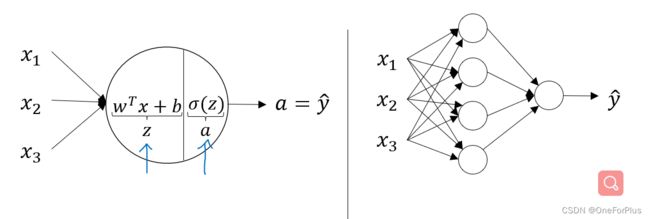
一个隐藏层的神经网络与逻辑回归单元的区别

向前传播公式：
$$Z^{[1]}=W^{[1]T}\ast X+b^{[1]}$$$$A^{[1]}=\sigma (Z^{[1]})$$$$Z^{[2]}=W^{[2]T}\ast A^{[1]}+b^{[2]}$$$$A^{[2]}=\sigma (Z^{[2]})$$

上标方括号对应相应层数，例如$Z^{[1]}$表示第一个隐藏层的Z。注意x那一层为第零层，也可以说x那一层不在层数计算范围内。

公式中的考虑：

1.此时$W^{[1]}$应是$(n,k)$维度，$X$为$(n,m)$维,则对应第一条等式计算过后$Z$和$A$应当是$(k,m)$维。相比于之前逻辑回归单元的$(1,m)$维，其相当于多了一个维度。$k$对应公式运算后的节点个数。

2.此时对应有两个$\sigma$不同层可以对应不同的激活函数。

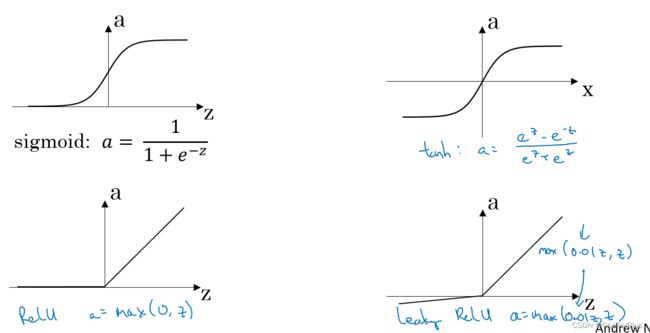
在隐藏层较常使用的有：
ReLU激活函数(用的较普遍):$A=max(0,Z)$
Leaky ReLU(带泄露的ReLU)激活函数:$A=max(0.01Z,Z)$
tanh激活函数:$A=\frac{e^Z-e^{-Z}}{e^Z+e^{-Z}}$ 范围为(-1,1)

在输出层常用的有：
sigmoid函数：$A=1/(1+e^{-Z})$ 范围为(0,1)

各函数图像如下

3.此时$W^{[2]}$应是$(1,k)$维度，$A^{[1]}$为$(k,m)$维,则对应第一条等式计算过后$Z$和$A$应当是$(1,m)$维。与之前逻辑回归单元的$(1,m)$维相等。$m$对应样本个数。

4.当层数更多时,$W^{[2]}$将跟之前的$W^{[1]}$一样有多一个维度，即可以是$(i,o)$之类的。而当输出结果不唯一时，$Z$和$A$维数也可以是多维，即类似$(i,m)$，则此时$i$对应输出结果数据数。当然这些应该都是后话了。

5.为什么要才有多层神经网络？我的理解是，单层节点能做到的有限，你可以理解为一个节点是对样本的一个侧面的逼近，多层节点则能从多个侧面多个维度逼近样本。
显然多层节点能更真实表现或者辨别数据。

向后传播公式：

$d{z}^{[2]}=a^{[2]}-y$

$d{W}^{[2]}=d{z}^{[2]}{a}^{[1]T}$

$d{b}^{[2]}=d{z}^{[2]}$

$d{z}^{[1]}=W^{[2]T}d{z}^{[2]}\ast g^{[1]}\prime z^{[1]}$

$d{W}^{[1]}=d{z}^{[1]}{x}^T$

$d{b}^{[1]}=d{z}^{[1]}$

“*”在等式中为点乘，区别点乘和叉乘

构建一个隐藏层的神经网络

1.初始化$W^{[1]}$,$b^{[1]}$,$W^{[2]}$,$b^{[2]}$

2.根据测试数据集(包含：$X$,$Y$,即有辨认数据，也有辨认结果数据)，算出$A^{[2]}$,$d{W}^{[1]}$,$d{b}^{[1]}$,$d{W}^{[2]}$,$d{b}^{[1]}$,$cost$.

3.循环num_iterations次数更新$W^{[1]}$,$b^{[1]}$,$W^{[2]}$,$b^{[2]}$,$A^{[2]}$,$d{W}^{[1]}$,$d{b}^{[1]}$,$d{W}^{[2]}$,$d{b}^{[1]}$。$cost$在这里是为了后期验证$W1$,$b1$,$W2$,$b2$的有效性，或者说可视化更新过程的一个东西。

4.得出最后的$W^{[1]}$,$b^{[1]}$,$W^{[2]}$,$b^{[2]}$,也就是获得一个训练后的有一个隐藏层的神经网络。

5.可以输入测试数据集测试回归单元的有效性了。

注意事项：
a.此时只有一个$W$,因为$W^{[1]}$和$W^{[2]}$被按列放在了矩阵$W$中了。通过正确的运算其就可以发挥$W^{[1]}$和$W^{[2]}$的作用了。
a.b的此时应当是$(k,1)$维,实际中通过python可以广播乘合适的矩阵。

以上为个人观点，如有不当之处请批评指正