论文总结:用基于注意力机制的卷积神经网络进行因果发现
Causal discovery with attention-based convolutional neural networks
文章目录
- Causal discovery with attention-based convolutional neural networks
-
- 问题描述
- 时序因果发现框架TCDF
-
- 时序预测
- 注意力解释
- 因果验证
- 时延发现
- 可改进点
- 参考文献
本文针对时序数据的因果推断,提出了一个 时序因果发现框架TCDF(Temporal Causal Discovery Framework),开创性地利用深度学习强大的表达能力发现时序数据中的因果关系,并构造因果关系图。TCDF使用了基于注意力机制的卷积神经网络和一个因果验证步骤。TCDF能学习出包含混杂因子和瞬时效应的因果关系图,也能通过解释CNN中的参数发现变量间的因果时延,还能发现特定情况下隐藏混杂因子的存在。通过对比可以发现,本文的工作为复杂系统的时序因果发现提供了一个全新的视角。
问题描述
时序因果发现的目标是给定时间序列 X = { x 1 , … , x n } X = \{x_1,\dots,x_n\} X={x1,…,xn},( x i = { x i 1 , x i 2 , … , x i t , … , x i T } x_i=\{x_i^{1},x_i^2,\dots,x_i^t,\dots,x_i^T\} xi={xi1,xi2,…,xit,…,xiT}),构造因果关系图,如下图所示,因果图中的有向边被标注为因果时延。时序因果推断则是根据因果关系图和其它变量在时刻 T T T以及 T T T之前的值预测变量在时刻 T T T的值。之所以会用到其它变量在时刻 T T T的值,是因为因果图中的变量间可能存在瞬时效应。
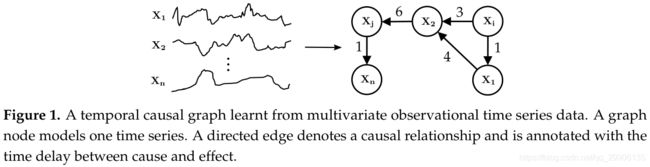
时序因果发现框架TCDF
时序数据的因果发现与非时序数据的因果发现最大的一点不同是,时序数据中包含时间属性,而原因一定不会晚于结果的发生,是判断因果方向的重要依据。TCDF包含四个部分:
- 时序预测:使用卷积神经网络对时序数据建模,针对每一个变量,用其它变量在时刻 T T T以及 T T T之前的值回归并预测该变量在时刻 T T T的值。
- 注意力解释:TCDF在卷积神经网络中采用了注意力机制,根据学习到的不同变量的注意力系数,可以将注意力系数解释为变量间的相关程度,低于一定阈值就可以认为两个变量没有因果关系。
- 因果验证:注意力机制只能发现可能的因果关系,需要进一步验证。
- 时延发现:除了因果发现,TCDF还能通过CNN中的参数发现变量间因果效应的时延。
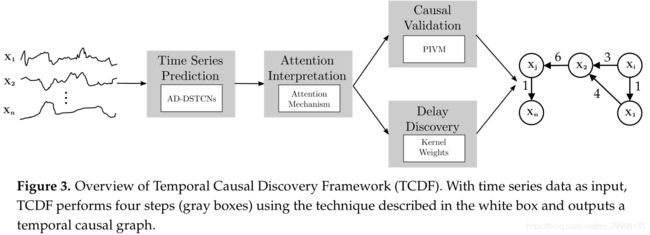
TCDF具体结构如下:
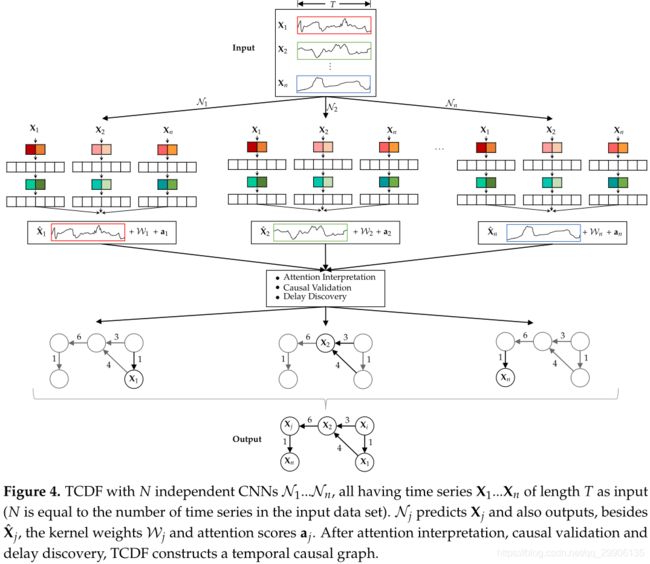
时序预测
本文的工作基于通用时序卷积网络(TCN)进行扩展。TCN为卷积神经网络架构,其中卷积核维度为1、长度为 K K K,有 L L L个隐藏层。对于单层网络,感受域(网络能感知到的时间步)为卷积核的长度 K K K,为了发现因果关系,感受域应该不小于因果时延。为扩大感受域,可以增加隐藏层的数量 L L L或卷积核的长度 K K K,CNN的感受域为 R C N N = 1 + ( L + 1 ) ( K − 1 ) = 1 + ∑ i = 0 L ( K − 1 ) (1) R_{CNN}=1+(L+1)(K-1)=1+\sum_{i=0}^{L}(K-1)\tag{1} RCNN=1+(L+1)(K−1)=1+i=0∑L(K−1)(1)而TCN则使用了扩张卷积(dilated convolutioon),卷积核以步长 f = c l f = c^l f=cl跳过部分输入,其中 f f f为扩张因子, c c c为扩张系数, l l l为卷积核所在的层。如Figure 5所示,扩张TCN(D-TCN)的感受域为 R D − T C N = 1 + ∑ l = 0 L ( K − 1 ) ⋅ c l (2) R_{D-TCN}=1+\sum_{l=0}^L(K-1)\cdot c^l\tag{2} RD−TCN=1+l=0∑L(K−1)⋅cl(2)
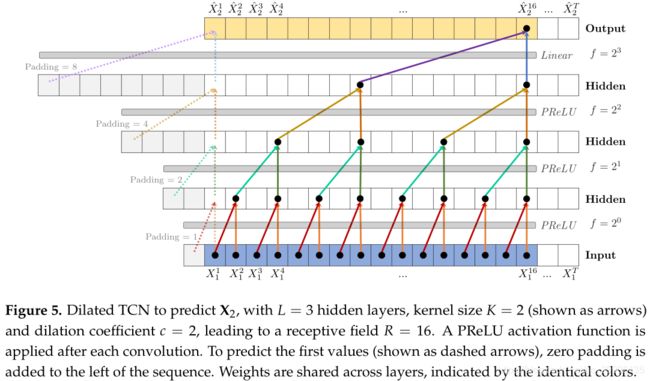
TCN只能对单变量时序建模,为利用多变量进行预测,TCDF将TCN的单通道输入扩展为多通道,每个通道对应于一个序列,如Figure 6所示。以预测变量 X 2 X_2 X2在时刻 T = 13 T=13 T=13时的值 X 2 13 X_2^{13} X213为例,需要输入其它变量 X j ≠ 2 t ∈ [ 1 , 13 ] X_{j\neq2}^{t\in{[1,13]}} Xj=2t∈[1,13]的值以及 X 2 t ∈ [ 1 , 12 ] X_2^{t\in[1,12]} X2t∈[1,12]的值,其中序列 X 2 X_2 X2采用左零填充使各通道输入序列长度一致,表示自因果关系。为了不丢失每个通道的信息,TCDF采用深度可分离卷积单独处理每个序列,只在网络最后一层进行融合。另外,为了确定每个变量与目标变量的相关程度,TCDF引入了注意力机制,为目标变量 X i X_i Xi设置注意力系数向量 a i = { a i 1 , a i 2 , ⋯ , a i n } a_i=\{a_i^1,a_i^2,\cdots,a_i^n\} ai={ai1,ai2,⋯,ain},将通道 j j j的输入与注意力系数 a i , j a_{i,j} ai,j相乘,表示变量 X j X_j Xj对 X i X_i Xi的影响程度。TCDF将该网络称为Attention-based Dilated Depthwise Separable Temporal Convolutional Network,AD-DSTCN,同时为了预测全体变量集,TCDF包含了 N N N个这样的AD-DSTCN。AD-DSTCN的网络层使用PReLU激活函数代替ReLU;为避免梯度消失问题,AD-DSRCN也对卷积层引入了残差连接 o = P R e L U ( x + F ( x ) ) (3) o = PReLU(x+F(x))\tag{3} o=PReLU(x+F(x))(3);AD-DSTCN用强监督的方法进行训练,最小化预测数据与真实数据的均方误差。
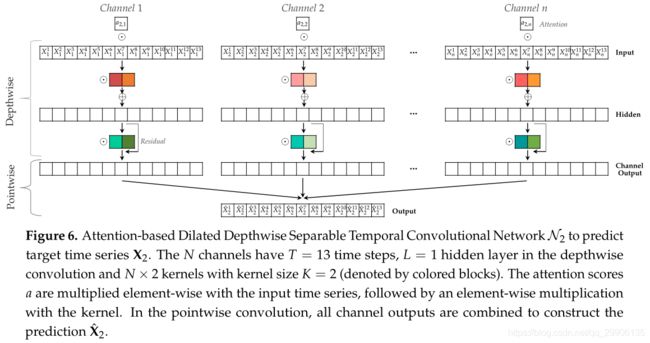
- Figure 6 中Channel 2的输入表示有问题,不应包含 X 2 13 X_2^{13} X213。
注意力解释
初始注意力向量 a i = [ 1 , 1 , ⋯ , 1 ] a_i=[1,1,\cdots,1] ai=[1,1,⋯,1],随着网络的训练, a i ∈ [ − ∞ , ∞ ] N a_i\in[-\infty,\infty]^N ai∈[−∞,∞]N。学术界通常将注意力分为软注意力 a i ∈ [ 0 , 1 ] N a_i\in[0,1]^N ai∈[0,1]N和硬注意力 a i ∈ { 0 , 1 } N a_i\in\{0,1\}^N ai∈{0,1}N。软注意力通常通过对注意力向量应用Softmax函数,使 ∑ i = 1 N a i , j = 1 \sum_{i=1}^Na_{i,j}=1 ∑i=1Nai,j=1。Softmax转换的一个局限是 σ ( a i , j ) ≠ 0 \sigma(a_{i,j})\neq 0 σ(ai,j)=0,但是一个变量与另一个变量之间只有有因果关系和无因果关系两种情况。而硬注意力通常因为离散表示而不可微分,无法用后向传播算法优化。因此本文用以下公式转换注意力系数:
h = H a r d S o f t m a x ( a ) = { σ ( a ) if a ≥ τ i 0 if a < τ i (4) h=HardSoftmax(a)=\begin{cases} \sigma(a) &\text{ if $a\ge\tau_i$ }\\ 0 &\text{ if $a\lt\tau_i$ } \end{cases}\tag{4} h=HardSoftmax(a)={σ(a)0 if a≥τi if a<τi (4)
转换后的注意力系数向量 a i a_i ai记作 h i h_i hi; τ j \tau_j τj的选择算法参考论文原文。
经过上述转换,可以得到变量 X i X_i Xi与 X j X_j Xj之间的注意力得分 h i , j h_{i,j} hi,j和 h j , i h_{j,i} hj,i,从而判断一个变量是不是另一个变量的可能原因,会出现四种情况(记变量 X u X_u Xu的可能原因集合为 P u P_u Pu):
- h i , j = 0 h_{i,j} = 0 hi,j=0, h j , i = 0 h_{j,i} = 0 hj,i=0: X i X_i Xi与 X j X_j Xj之间不存在因果关系。
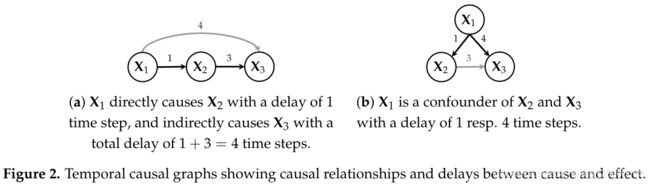
- h i , j = 0 h_{i,j} = 0 hi,j=0, h j , i > 0 h_{j,i} > 0 hj,i>0:将 X j X_j Xj加入 P i P_i Pi,因为以下两种情况(如Figure 2所示):
(a) X j X_j Xj是 X i X_i Xi的直接或间接原因。
(b) X j X_j Xj与 X i X_i Xi之间存在混杂因子,而且混杂因子对 X j X_j Xj的时延比对 X i X_i Xi的大。 - h i , j > 0 h_{i,j} > 0 hi,j>0, h j , i = 0 h_{j,i} = 0 hj,i=0:将 X i X_i Xi加入 P j P_j Pj,因为以下两种情况(如Figure 2所示):
(a) X i X_i Xi是 X j X_j Xj的直接或间接原因。
(b) X i X_i Xi与 X j X_j Xj之间存在混杂因子,而且混杂因子对 X i X_i Xi的时延比对 X j X_j Xj的大。 - h i , j > 0 h_{i,j} > 0 hi,j>0, h j , i > 0 h_{j,i} > 0 hj,i>0:将 X j X_j Xj加入 P i P_i Pi,将 X i X_i Xi加入 P j P_j Pj,因为以下两种情况:
(a) X i X_i Xi与 X j X_j Xj之间存在双向因果关系。
(b) 存在混杂因子对 X j X_j Xj与 X i X_i Xi的时延一样大。
通过对注意力的解释,AD-DSTCN可以发现可能的因果关系,但仍不能完全确定。
因果验证
TCDF使用排列重要性(Permutation Importance,PI)验证因果关系。排列重要性是指,打乱原因变量的时序(不会改变变量的分布,但能消除变量中的时间信息),用AD-DSTCN重新预测目标变量,预测误差的变化程度。如果两个变量之间没有因果关系,则改变其中一个变量的顺序几乎不会影响AD-DSTCN的预测误差;否则预测误差会大幅提高。预测误差的变化程度阈值计算方法参考论文原文。该方法被称为Permutaion Importance Validation Method,PIVM。
如果所有混杂因子都被观测到,PIVM能正确判断变量间的因果关系,因为只有混杂变量是预测目标变量所必需的。但当混杂因子未被观测时,PIVM可能无法正确判断。
基于case2-4,两个变量相互相关有三种原因:存在因果关系,存在已观测混杂因子,存在未观测混杂因子。如果是因为相互之间的因果关系,PIVM能发现两个变量都以一定的时延影响对方(case 4a);如果是因为已观测混杂因子,PIVM会发现两个变量相关而不具有因果效应;如果是因为未观测的混杂因子,PIVM会发现两个变量互为因果。
为什么如果是因为未观测的混杂因子,两个变量就互为因果?
如果隐藏混杂因子对两个变量的因果效应时延不相等(case 2b 和case 3b),PIVM会错误地认为一个变量是另一个变量的原因,如Figure 8a所示。当隐藏混杂因子对两个变量的因果效应时延相同时(case 4b),PIVM会发现两个变量间互有瞬时因果关系,从而推测出隐藏混杂因子的存在(现实中不会有两个变量互有瞬时因果效应),如Figure 8b所示。

时延发现
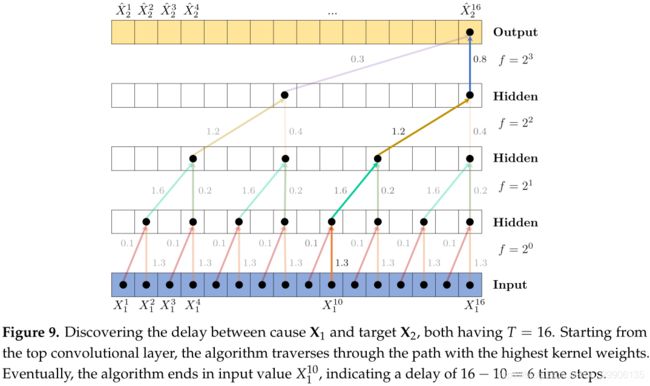
除了发现因果关系的存在性,TCDF还能发现原因到影响结果所用的时间步,即因果效应时延。卷积网络中每一层内的卷积核权重是共享的,不仅能减少网络参数,还能用于解释因果时延。如Figure 9所示,卷积操作是线性的,因此卷积核的 K K K个权重的大小表示了不同时间步对预测目标变量的重要性,通过找出各层卷积核权重最大值组成的路径,可以找到正确的因果时延。从Figure 9中也可以看出,要想找到正确的因果时延,整个网络的感受域不能小于变量间最大的因果时延。
可改进点
参考文献
[1] Nauta M, Bucur D, Seifert C. Causal discovery with attention-based convolutional neural networks. Machine Learning and Knowledge Extraction, 2019, 1(1): 312–340.