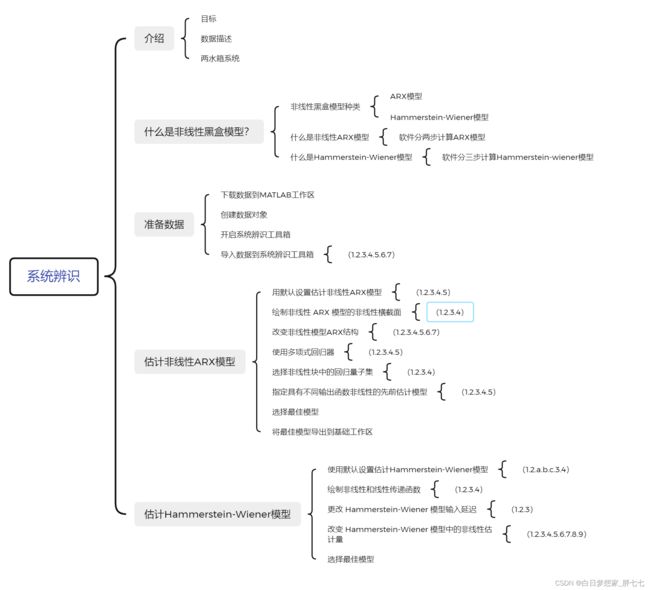
MATLAB-使用系统识别应用程序识别非线性黑盒模型
Identify Nonlinear Black-Box Models Using System Identification App - MATLAB & Simulink - MathWorks 中国
目录
编辑
介绍
目标
数据描述
什么是非线性黑盒模型?
非线性黑盒模型的类型
非线性 ARX 模型
什么是非线性 ARX 模型?
什么是 Hammerstein-Wiener 模型?
准备数据
将数据加载到 MATLAB 工作区
创建数据对象
启动系统识别应用程序
将数据对象导入系统识别应用程序
估计非线性 ARX 模型
使用默认设置估计非线性 ARX 模型
绘制非线性 ARX 模型的非线性横截面
更改非线性 ARX 模型结构
使用多项式回归器
选择非线性块中的回归量子集
指定具有不同输出函数非线性的先前估计模型
选择最佳模型
将最佳模型导出到基础工作区
估计 Hammerstein-Wiener 模型
使用默认设置估计 Hammerstein-Wiener 模型
绘制非线性和线性传递函数
更改 Hammerstein-Wiener 模型输入延迟
改变 Hammerstein-Wiener 模型中的非线性估计量
选择最佳模型
介绍
目标
从单输入/单输出 (SISO) 数据估计和验证非线性模型,以找到最能代表您的系统动态的模型。
完成本教程后,您将能够使用系统识别应用程序完成以下任务:
- 将数据对象从 MATLAB® 工作区导入应用程序。
- 从数据中估计和验证非线性模型。
- 绘制并分析非线性行为。
数据描述
本教程使用数据文件 twotankdata.mat,其中包含双罐系统的 SISO 时域数据,如下图所示。
在双水箱系统中,水通过管道流入水箱 1,排入水箱 2,然后通过水箱 2 底部的小孔离开系统。系统的测量输入 u(t) 是施加的电压 到将水送入水箱 1 的泵(以伏特为单位)。 测量输出 y(t) 是下水箱中水的高度(以米为单位)。
根据伯努利定律,该定律指出流过水箱底部小孔的水非线性地取决于水箱中的水位,您预计输入和输出数据之间的关系是非线性的。
twotankdata.mat 包含 3000 个样本,采样时间为 0.2 秒。
什么是非线性黑盒模型?
非线性黑盒模型的类型
您可以估计单输出和多输出时域数据的非线性离散时间黑盒模型。 您可以从两种类型的非线性黑盒模型结构中进行选择:
-
非线性 ARX 模型
- Hammerstein-Wiener 模型
您只能从输入/输出数据估计 Hammerstein-Wiener 黑盒模型。 这些模型不支持没有输入的时间序列数据。
有关估计非线性黑盒模型的更多信息,请参阅非线性模型识别。Nonlinear Model Identification.
什么是非线性 ARX 模型?
非线性 ARX 模型由模型回归量和输出函数组成。 输出函数包含一个或多个映射对象,每个模型输出一个。 每个映射对象都可以包括一个线性和非线性函数,它们作用于模型回归器以给出模型输出和该输出的固定偏移量。 此框图表示模拟场景中单输出非线性 ARX 模型的结构。
该软件分两个阶段计算非线性 ARX 模型输出 y:
1.它根据当前和过去的输入值以及过去的输出数据计算回归值。
在最简单的情况下,回归量是延迟的输入和输出,例如 u(t-1) 和 y(t-3)。这种回归量称为线性回归量。您可以使用 linearRegressor 对象指定线性回归量。您还可以使用线性 ARX 模型阶数作为输入参数来指定线性回归量。有关详细信息,请参阅非线性 ARX 模型阶数和延迟Nonlinear ARX Model Orders and Delay。但是,第二种方法将您的回归器集限制为具有连续延迟的线性回归器。要创建多项式回归器,请使用 polynomialRegressor 对象。要创建包含延迟输入和输出变量的正弦和余弦函数的周期性回归量,请使用periodicRegressor 对象。您还可以指定自定义回归器,它们是延迟输入和输出的非线性函数。例如,u(t–1)y(t–3) 是一个自定义回归器,它将输入和输出的实例相乘。使用 customRegressor 对象指定自定义回归量。
您可以将任何回归量作为输入分配给输出函数的线性功能块、非线性功能块或两者。
2.它使用输出功能块将回归量映射到模型输出。输出功能块可以包括并行的多个映射对象线性、非线性和偏移块。例如,考虑以下等式:
Q 是一个投影矩阵,可以使计算得到良好的条件。 d 是一个标量偏移,它被添加到线性和非线性块的组合输出中。 F(x) 的确切形式取决于您选择的输出函数。 您可以从可用的映射对象中进行选择,例如树分区网络、小波网络和多层神经网络。 您还可以从输出函数中排除线性或非线性功能块。
在估计非线性 ARX 模型时,软件会计算模型参数值,例如 L、r、d、Q 和其他指定 g 的参数。
生成的非线性 ARX 模型是存储所有模型数据的 idnlarx 对象,包括模型回归量和输出函数的参数。 有关这些对象的详细信息,请参阅非线性模型结构 Nonlinear Model Structures.
什么是 Hammerstein-Wiener 模型?
此框图表示 Hammerstein-Wiener 模型的结构:
在这里,
- f 是一个非线性函数,它将输入数据 u(t) 转换为 w(t) = f(u(t))。
w(t) 是一个内部变量,是 Input Nonlinearity 模块的输出,与 u(t) 具有相同的维度。
- B/F 是将 w(t) 转换为 x(t) = (B/F)w(t) 的线性传递函数。
x(t) 是一个内部变量,是线性模块的输出,与 y(t) 具有相同的维度。
B 和 F 类似于线性输出误差模型中的多项式。 有关输出误差模型的更多信息,请参阅什么是多项式模型?。
对于 ny 个输出和 nu 个输入,线性块是一个包含条目的传递函数矩阵:
其中 j = 1,2,...,ny 和 i = 1,2,...,nu。
- h 是一个非线性函数,它将线性块 x(t) 的输出映射到系统输出 y(t),因为 y(t) = h(x(t))。
因为 f 作用于线性模块的输入端口,所以这个函数称为输入非线性。 类似地,由于 h 作用于线性模块的输出端口,这个函数称为输出非线性。 如果您的系统包含多个输入和输出,则必须为每个输入和输出信号定义函数 f 和 h。 您不必在模型结构中同时包含输入和输出非线性。 当模型仅包含输入非线性 f 时,称为 Hammerstein 模型。 类似地,当模型只包含输出非线性 h 时,称为维纳模型。
该软件分三个阶段计算 Hammerstein-Wiener 模型输出 y:
1.根据输入数据计算 w(t) = f(u(t))。
w(t) 是线性传递函数 B/F 的输入。
输入非线性是一个静态(无记忆)函数,其中给定时间 t 的输出值仅取决于时间 t 的输入值。
您可以将输入非线性配置为 sigmoid 网络、小波网络、饱和度、死区、分段线性函数、一维多项式或自定义网络。您还可以消除输入非线性。
2.使用 w(t) 和初始条件计算线性块的输出:x(t) = (B/F)w(t)。
您可以通过指定分子 B 和分母 F 的顺序来配置线性块。
通过使用非线性函数 h 将线性块 x(t) 的输出转换为 y(t) = h(x(t)) 来计算模型输出。
3.与输入非线性相似,输出非线性是一个静态函数。您可以按照与输入非线性相同的方式配置输出非线性。您还可以消除输出非线性,例如 y(t) = x(t)。
生成的模型是存储所有模型数据的 idnlhw 对象,包括模型参数和非线性估计器。有关这些对象的更多信息,请参阅非线性模型结构。Nonlinear Model Structures.
准备数据
将数据加载到 MATLAB 工作区
通过在 MATLAB 命令行窗口中键入以下命令来加载 twotankdata.mat 中的示例数据:
load twotankdata此命令将以下两个变量加载到 MATLAB Workspace 浏览器中:
- u 是输入数据,它是施加到将水送入水箱 1 的泵的电压(以伏特为单位)。
- y 是输出数据,即 Tank 2 中的水位高度(以米为单位)。
创建数据对象
System Identification Toolbox™ 数据对象将数据值和数据属性封装到单个实体中。 您可以使用 System Identification Toolbox 命令方便地将这些数据对象作为单个实体进行操作。
您必须已将样本数据加载到 MATLAB 工作区,如将数据加载到 MATLAB 工作区中所述。
使用以下命令创建两个 iddata 数据对象 ze 和 zv,其中 ze 包含用于模型估计的数据,zv 包含用于模型验证的数据。 Ts 是采样时间。
Ts = 0.2; % Sample time is 0.2 sec
z = iddata(y,u,Ts);
% First 1000 samples used for estimation
ze = z(1:1000);
% Remaining samples used for validation
zv = z(1001:3000);要查看 iddata 对象的属性,请使用 get 命令。 例如:
get(ze)MATLAB 软件返回以下数据属性和值:
Domain: 'Time'
Name: ''
OutputData: [1000x1 double]
y: 'Same as OutputData'
OutputName: {'y1'}
OutputUnit: {''}
InputData: [1000x1 double]
u: 'Same as InputData'
InputName: {'u1'}
InputUnit: {''}
Period: Inf
InterSample: 'zoh'
Ts: 0.2000
Tstart: 0.2000
SamplingInstants: [1000x0 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []
要修改数据属性,请使用点表示法。 例如,要分配标记绘图轴的通道名称和单位,请在 MATLAB 命令行窗口中键入以下语法:
% Set time units to minutes
ze.TimeUnit = 'sec';
% Set names of input channels
ze.InputName = 'Voltage';
% Set units for input variables
ze.InputUnit = 'V';
% Set name of output channel
ze.OutputName = 'Height';
% Set unit of output channel
ze.OutputUnit = 'm';
% Set validation data properties
zv.TimeUnit = 'sec';
zv.InputName = 'Voltage';
zv.InputUnit = 'V';
zv.OutputName = 'Height';
zv.OutputUnit = 'm';要验证 ze 的 InputName 属性是否已更改,请键入以下命令:
ze.inputname属性名称(例如 InputName)不区分大小写。 您还可以缩写以 Input 或 Output 开头的属性名称,方法是在属性名称中用 u 代替 Input,用 y 代替 Output。 例如,OutputUnit 等价于 yunit。小费
启动系统识别应用程序
要打开 System Identification 应用程序,请在 MATLAB 命令行窗口中键入以下命令:
systemIdentification默认会话名称 Untitled 出现在标题栏中。
将数据对象导入系统识别应用程序
您可以将数据对象从 MATLAB 工作区导入应用程序。
您必须已创建数据对象,如创建 iddata 对象中所述,并打开应用程序,如启动系统标识应用程序中所述。
要导入数据对象:
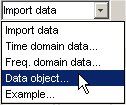
- 在系统标识应用程序中,选择导入数据 > 数据对象。
此操作将打开“导入数据”对话框。
2. 在 Object 字段中输入 ze 以导入估计数据。 按 Enter。
此操作将对象信息输入到导入数据字段中。
单击更多可查看有关此数据的其他信息,包括通道名称和单位。
3.单击导入以将名为 ze 的图标添加到系统标识应用程序。
4.在 Import Data 对话框中,在 Object 字段中键入 zv 以导入验证数据。 按 Enter。
5.单击导入以将名为 zv 的图标添加到系统标识应用程序。
6.在“导入数据”对话框中,单击“关闭”。
7在 System Identification 应用程序中,将验证数据 zv 图标拖动到验证数据矩形。 估计数据 ze 图标已在工作数据矩形中指定。
或者,右键单击 zv 图标以打开“数据/模型信息”对话框。 选中用作验证数据复选框。 单击应用,然后单击关闭以将 zv 添加到验证数据矩形。
系统标识应用程序现在类似于下图。
估计非线性 ARX 模型
使用默认设置估计非线性 ARX 模型
在本教程的这一部分中,您将使用默认模型结构和估计选项来估计非线性 ARX 模型。
您必须已经准备好数据,如准备数据中所述。 有关非线性 ARX 模型的更多信息,请参阅什么是非线性 ARX 模型?。 What Is a Nonlinear ARX Model?.
本教程中的插图代表一个典型的系统识别应用程序会话。 您的结果可能与图像中的结果不完全匹配。
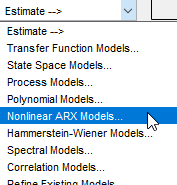
1.在系统识别应用程序中,选择估计 > 非线性模型。
此操作将打开“估计非线性 ARX 模型”对话框。
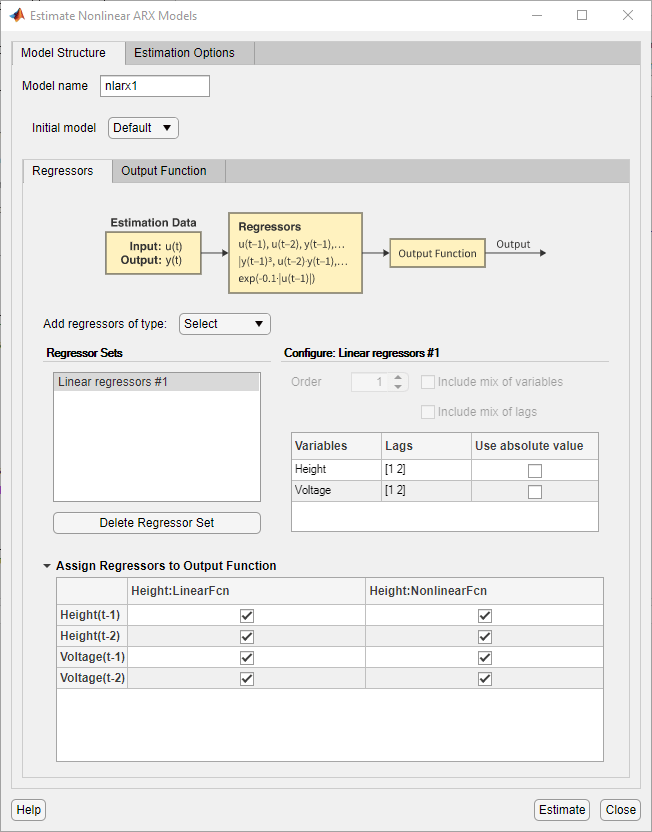
该对话框包含两个选项卡 - 模型结构和估计选项。
模型结构选项卡包含配置模型结构的参数,例如回归量的选择和输出函数的类型。 在模型名称中指定要估计的模型的名称。 默认模型名称为 nlarx1。
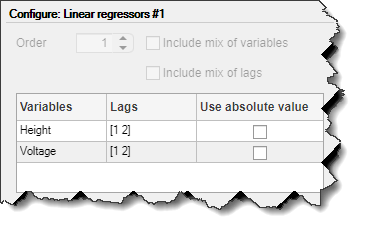
使用回归器选项卡创建要使用的回归器集。 默认情况下,应用程序会在每个变量中创建一个带有滞后 [1 2] 的线性回归器集,并将该回归器作为线性回归器 #1 存储在“回归器集”区域中。 此面板包含一个表格,允许您修改用于每个变量的滞后。
配置面板配置:线性回归器 #1 包含一个表格,显示回归器集使用的滞后值。 您可以修改这些滞后。
回归量分配表将回归量分配给输出函数列出了回归量名称和回归量分配给输出函数组件。
表中的回归变量分配为输出高度生成模型:
Height(t) = f(Height(t-1), Height(t-2),Voltage(t-1),Voltage(t-2))
高度(t) = f(高度(t-1)、高度(t-2)、电压(t-1)、电压(t-2))
这里,f(.) 是将回归量映射到输出的静态非线性函数。 要选择 f(.) 及其相关参数,请使用输出函数选项卡。
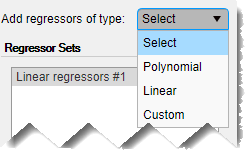
您可以通过在添加回归器类型中选择回归器类型来添加更多回归器集,例如多项式和自定义公式。
此示例仅使用线性回归量 #1。
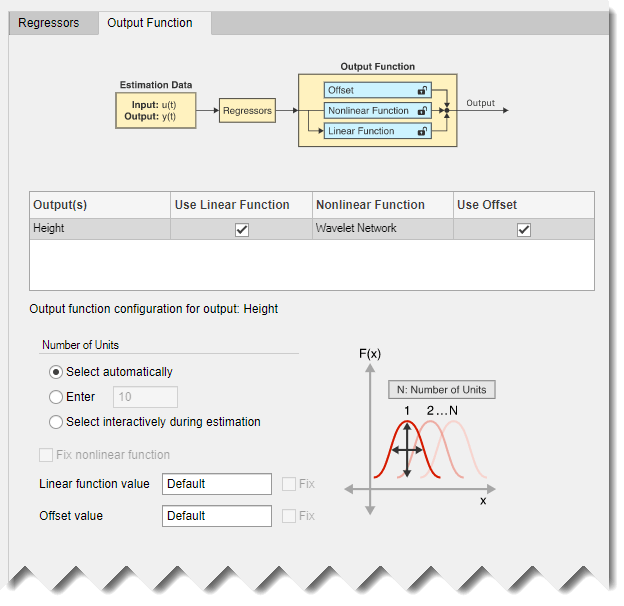
2.选择输出函数选项卡。
该选项卡显示应用程序选择小波网络作为输出函数 f(.) 的默认类型。 该函数使用线性函数、非线性函数(缩放小波的总和)和偏移项的总和来计算输出。 该选项卡还显示一组配置参数。 该函数使用的小波数量配置为在估计期间自动选择。 您可以修改此选择。 您还可以修改线性系数和偏移量的初始值。 对于第一个估计,保留默认选项。
3.单击估计。
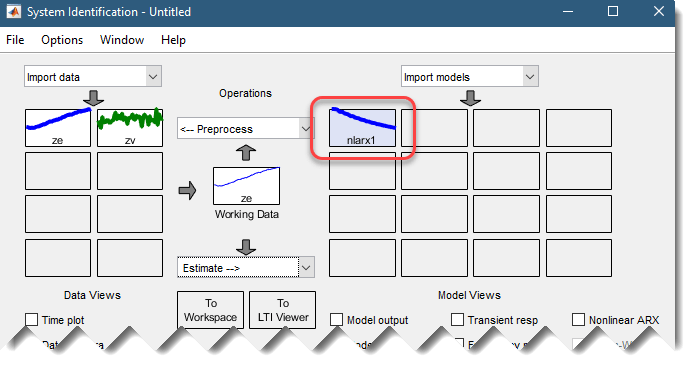
此操作将模型 nlarx1 添加到系统识别应用程序的模型板上,如下图所示。
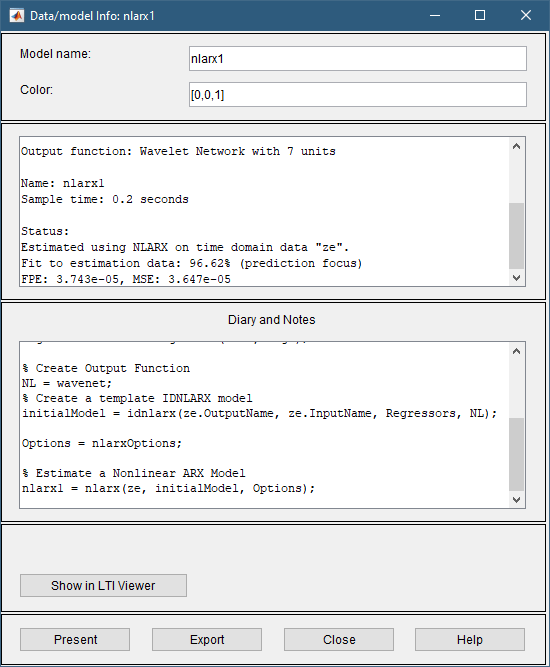
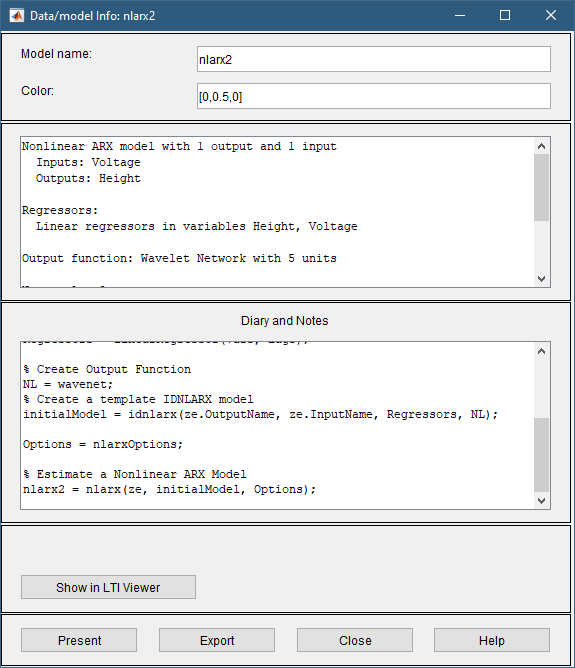
4.双击或右键单击模型图标 nlarx1 模型板显示有关估计模型的信息。 顶部区域描述了模型结构和估计结果(使用的数据、拟合百分比和其他质量指标)。 底部区域(日记和笔记)显示了 MATLAB 脚本,您可以使用该脚本在命令行中重现估计结果。
使用具有预测焦点的估计数据集计算拟合 (%)。 而不是验证数据集。 但是,下一步中的模型输出图会将拟合与验证数据集进行比较。 要查看模型如何模拟独立验证数据集的响应,请使用模型输出图,如以下步骤中所述。
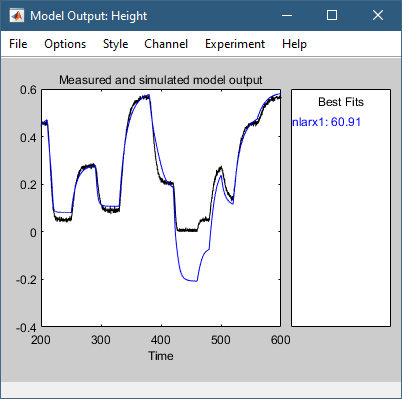
5 在 System Identification 应用程序的 Model Views 区域中,选择 Model output。 此操作使用输入验证数据作为模型的输入来模拟模型,并将模拟输出绘制在输出验证数据之上。
模型输出图的最佳拟合区域使用拟合优度的归一化均方根 (NRMSE) 度量显示模型输出和验证数据输出之间的一致性。 该协议在 400-500 时间跨度内较差。
绘制非线性 ARX 模型的非线性横截面
执行以下过程以在非线性 ARX 模型图上查看作为回归量函数的非线性形状。
1.在 System Identification 应用程序中,选中 Nonlinear ARX 复选框以查看非线性横截面。
默认情况下,该图显示输出回归量 Height(t-1) 和 Height(t-2) 之间的关系。 该图在下图中显示了一个规则平面。 因此,回归量和输出之间的关系近似为线性平面。
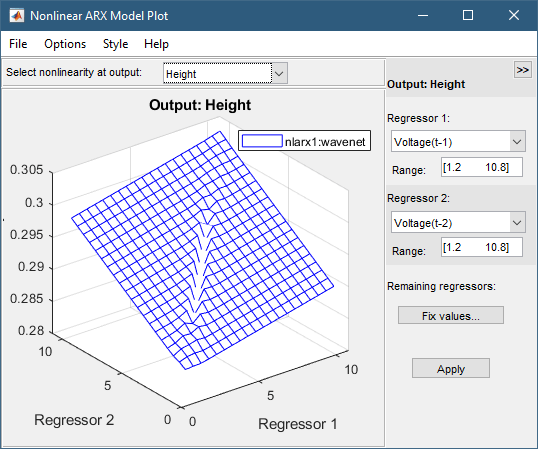
2.在非线性 ARX 模型图窗口中,将回归器 1 设置为电压 (t-1)。 将回归器 2 设置为电压 (t-2)。 单击应用。
这些回归量与输出之间的关系是非线性的,如下图所示。
3.要旋转非线性曲面,请选择样式 > 旋转 3D 并将绘图拖动到新方向。
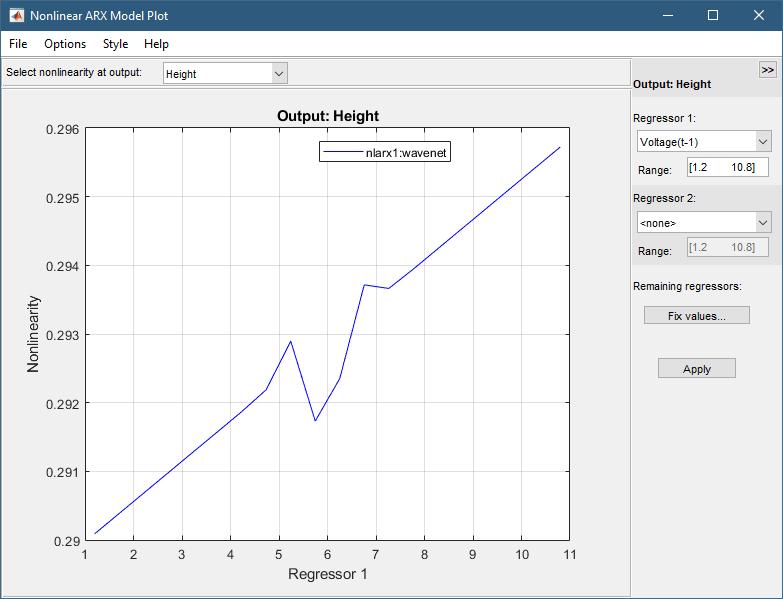
4.要显示回归量 1 的一维横截面,请将回归量 2 设置为无,然后单击应用。 下图显示了回归量 1 产生的非线性幅度,它表示时移电压信号 Voltage(t-1)。
更改非线性 ARX 模型结构
在本教程的这一部分,您将估计具有特定输入延迟和非线性设置的非线性 ARX 模型。 通常,您通过反复试验来选择模型顺序,直到您获得一个能够准确拟合数据的模型。
您必须已经使用默认设置估计了非线性 ARX 模型,如使用默认设置估计非线性 ARX 模型中所述。
1.在估计非线性 ARX 模型对话框中,选择模型结构选项卡,然后选择回归器选项卡。
2.在配置:线性回归器 #1 面板中,将电压变量滞后更改为 [3 4]。 这是因为数据表明输入和输出之间至少存在 3 个样本滞后。
此操作更新回归量列表以显示电压 (t-3) 和电压 (t-4) — 具有三个样本的最小延迟的项。
3. 单击估计。
此操作将模型 nlarx2 添加到系统识别应用程序并更新模型输出窗口以包含此模型。 双击主应用程序窗口模型板上的 nlarx2 图标显示估计结果。
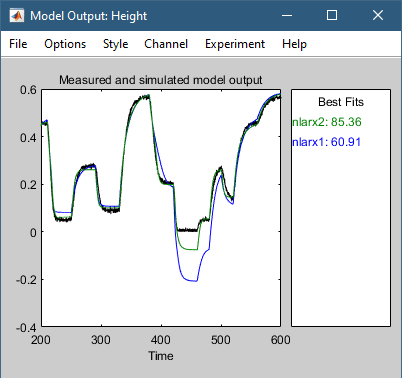
该应用程序还更新模型输出图以显示模型 nlarx2 与验证数据集 zv 的拟合。 该图显示,选择正确的输入变量滞后可以提高拟合度。
4.在估计非线性 ARX 模型对话框中,选择模型结构选项卡,然后选择回归器选项卡。
5.选择输出函数选项卡。
6.对于 Number of Units,选择 Enter 并输入 6。设置特定数字通过直接指定 Wavelet Network 使用的小波数量来控制非线性函数的灵活性。
7单击估计。
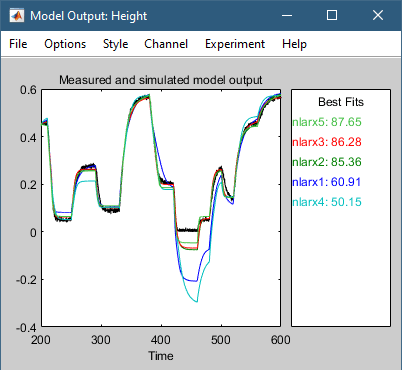
此操作将模型 nlarx3 添加到系统识别应用程序。 它还会更新模型输出窗口,如下图所示。
使用多项式回归器
您可以估计非线性 ARX 模型,该模型使用滞后变量的更高幂作为回归量。 在此示例中,您将添加滞后变量的二阶多项式,包括交叉项。
1.在 Estimate Nonlinear ARX Models 对话框中,选择 Model Structure 选项卡,然后选择 Regressors 选项卡。
2.展开添加类型的回归量并选择多项式。
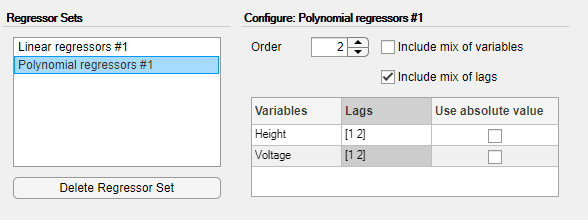
此操作将称为多项式回归量 #1 的多项式回归量集添加到回归量集列表中。 默认情况下,该集合配置为生成 2 阶回归量,如配置面板中所示。
3. 将电压滞后更改为 [3 4]。
4.选择包括变量组合以包括所有交叉项。 除了线性回归器 #1 贡献的四个之外,此操作向模型添加了十个二阶回归器。
5单击估计。 此操作将模型 nlarx4 添加到应用程序。 该应用程序更新模型输出图,如下图所示。
从图中可以看出,多项式回归量的加入并没有提高模型的泛化能力。 也就是说,该模型没有在模型输出和独立验证数据的测量输出之间提供更好的拟合。 此结果通常是过度拟合的情况,即模型包含的回归量比绝对需要的多。
选择非线性块中的回归量子集
您可以估计一个非线性 ARX 模型,该模型仅包含作为非线性模块输入的回归量子集。 默认情况下,非线性块中使用所有回归量。 在本教程的这一部分中,您仅将一部分回归量分配给非线性模块。
您必须已指定模型结构,如更改非线性 ARX 模型结构中所述。
1.在估计非线性 ARX 模型对话框中,选择模型结构选项卡,然后选择回归器选项卡。
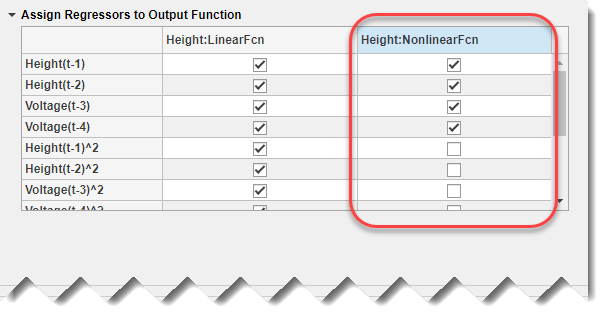
2.如果折叠,展开将回归器分配给输出函数面板。
3.从表的 Height:NonlinearFcn 列中清除所有二阶回归量的选择。 另外,从 Height:LinearFcn 中清除所有带有交叉项的回归变量(即由 2 个项的乘积组成的回归变量)的选择
4.单击估计。
此操作将模型 nlarx5 添加到系统识别应用程序。 它还会更新模型输出窗口。
该模型显示出改进的泛化能力。
指定具有不同输出函数非线性的先前估计模型
您可以通过对模型结构进行系统变化来估计一系列非线性 ARX 模型,并将每个新模型基于先前估计模型的配置。 在本教程的这一部分中,您将估计一个非线性 ARX 模型,它与现有模型 (nlarx3) 相似,但在输出函数中具有不同的非线性。
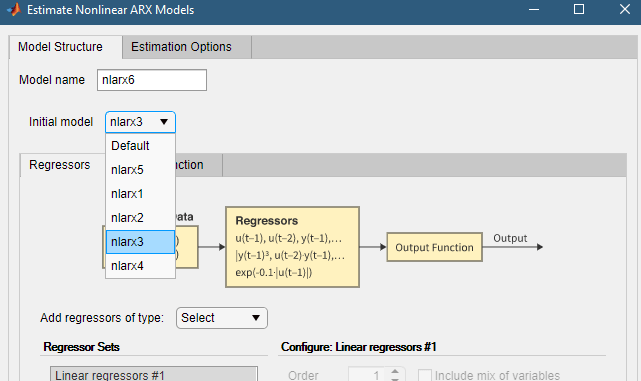
1.在估计非线性 ARX 模型对话框中,选择模型结构选项卡。
2.从初始模型中选择 nlarx3。 这会将“回归量”和“输出函数”选项卡中显示的属性设置为对应于 nlarx3 的值。
3.选择输出函数选项卡。
4.在表格中,将 Nonlinear Function 的选择更改为 Sigmoid Network。 这将输出函数设置为 sigmoid 网络。
5.
6.在输入单位数中,输入 6。
7.单击估计。
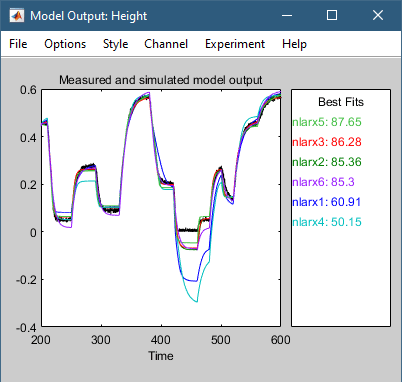
此操作将模型 nlarx6 添加到系统识别应用程序。 它还会更新模型输出图,如下图所示。
选择最佳模型
最好的模型是准确描述动力学的最简单的模型。 结果表明,基于此示例探索的各种模型结构选择,模型 nlarx3 是该数据的最佳 idnlarx 模型的候选者。
将最佳模型导出到基础工作区
将 nlarx3 图标拖到系统识别应用程序主窗口中的 To Workspace 框。 或者,双击 nlarx3 图标以打开其信息板。 从那里,单击导出以将模型导出到基础工作区。
估计 Hammerstein-Wiener 模型
使用默认设置估计 Hammerstein-Wiener 模型
在本教程的这一部分中,您将使用默认模型结构和估计选项来估计非线性 Hammerstein-Wiener 模型。
您必须已经准备好数据,如准备数据中所述。 有关非线性 ARX 模型的更多信息,请参阅什么是 Hammerstein-Wiener 模型?
本教程中的插图代表一个典型的系统识别应用程序会话。 您的结果可能与图像中的结果不完全匹配。
1.在 System Identification 应用程序中,选择 Estimate > Hammerstein-Wiener Models 以打开 Estimate Hammerstein-Wiener Models 对话框。 该对话框包含两个选项卡 - 模型结构和估计选项。
2.检查默认模型结构。 模型结构选项卡包含三个选项卡,模型的每个组件一个选项卡。 这些组件是输入非线性、线性动态模块和输出非线性。
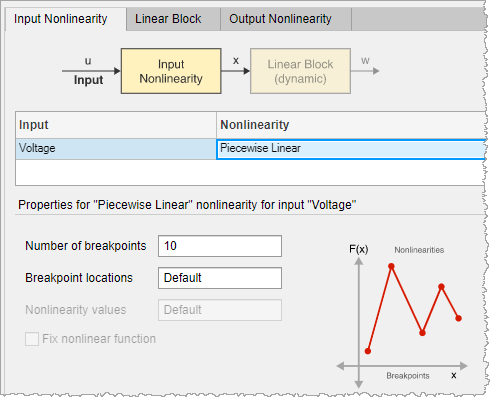
a.选择输入非线性选项卡。 默认非线性是具有 10 个断点的分段线性函数。
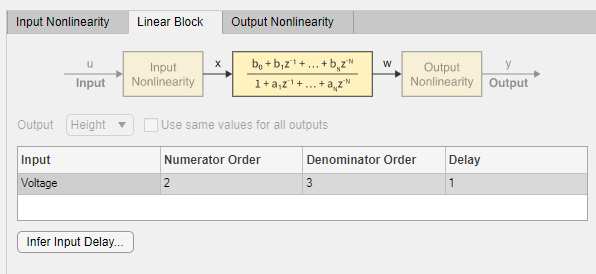
b.选择线性块选项卡。 线性传递函数的分子阶为 2,这意味着 z-1 中的二阶多项式,分母阶为 3,输入延迟为 1 个样本。
c.选择输出非线性选项卡。 与输入非线性选项卡一样,默认非线性是具有 10 个断点的分段线性函数。
3.单击估计。
此操作估计 Hammerstein-Wiener 模型的参数以最小化模型输出和测量输出 (ze.OutputData) 之间的差异。 估计的参数是:
a.输入和输出分段线性函数的断点位置(x 和 y 坐标)。
b.构成线性块传递函数的分子和分母多项式系数。
该软件将估计的模型 nlhw1 添加到系统识别应用程序的模型板上。
4.在 System Identification 应用程序中,选中 Model output 复选框。
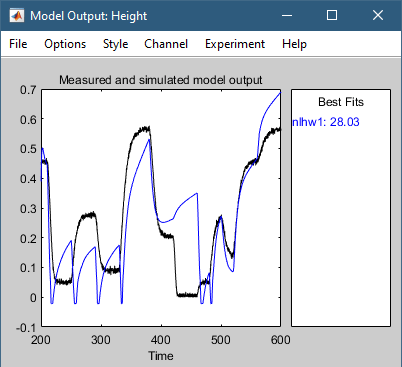
此操作使用输入验证数据作为模型的输入来模拟模型,并将模拟输出绘制在输出验证数据之上。 请注意,验证数据设置为 zv。
模型输出窗口的最佳拟合区域显示模型输出和验证数据输出之间的一致性。
模型 nlhw1 无法很好地验证。 对 zv.OutputData 的拟合很差。
绘制非线性和线性传递函数
您可以在 Hammerstein-Wiener 图上绘制模型的输入/输出非线性和线性传递函数。
在 System Identification 应用程序中,选择 Hamm-Wiener 以查看 Hammerstein-Wiener 模型图。
该图显示了输入非线性,如下图所示。
2.单击 Hammerstein-Wiener 模型图窗口顶部的 yNL 矩形。
绘图更新以显示输出非线性。
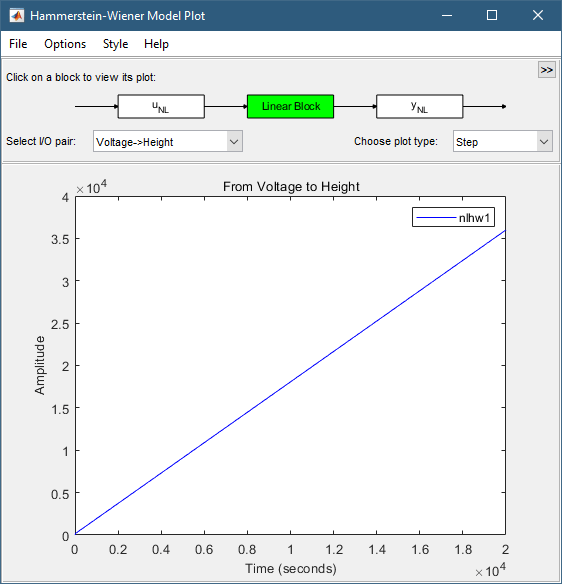
3.单击 Hammerstein-Wiener 模型图窗口顶部的线性块矩形。
绘图更新以显示线性传递函数的阶跃响应。
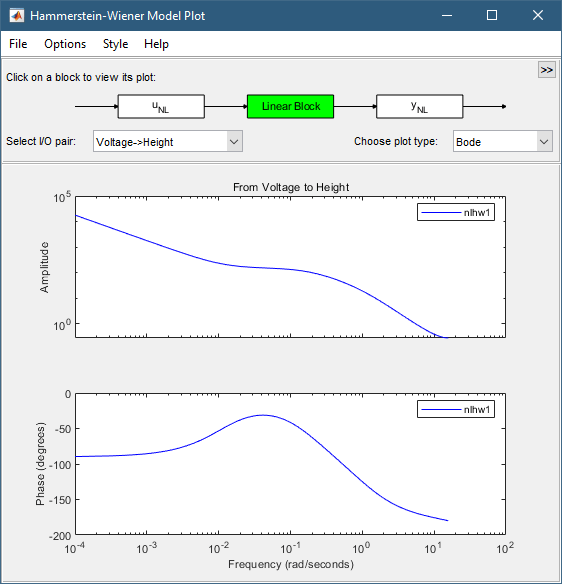
4.在选择绘图类型列表中,选择波德。 此操作显示线性传递函数的波特图。
更改 Hammerstein-Wiener 模型输入延迟
在本教程的这一部分中,您将估计具有特定模型阶数和非线性设置的 Hammerstein-Wiener 模型。 通常,您会通过反复试验来选择模型顺序和延迟,直到您获得对数据产生令人满意的拟合的模型。
您必须已经使用默认设置估计了 Hammerstein-Wiener 模型,如使用默认设置估计 Hammerstein-Wiener 模型中所述。
1.在估计 Hammerstein-Wiener 对话框中,选择模型结构选项卡,然后选择线性块选项卡。
2.对于电压输入通道,双击相应的输入延迟 (nk) 单元格并输入值 3。
3.单击估计。
此操作将模型 nlhw2 添加到系统识别应用程序并更新模型输出图,如下图所示。
模型输出窗口的最佳拟合面板显示 nlhw2 拟合的质量,这是对模型 nlhw1 的改进。
改变 Hammerstein-Wiener 模型中的非线性估计量
在示例的这一部分中,您通过更改其非线性估计器来修改默认的 Hammerstein-Wiener 模型结构。
如果您知道您的系统包含饱和或死区非线性,您可以在模型中指定这些专门的非线性估计器。 分段线性、小波网络和 Sigmoid 网络是用于一般非线性近似的非线性估计器。
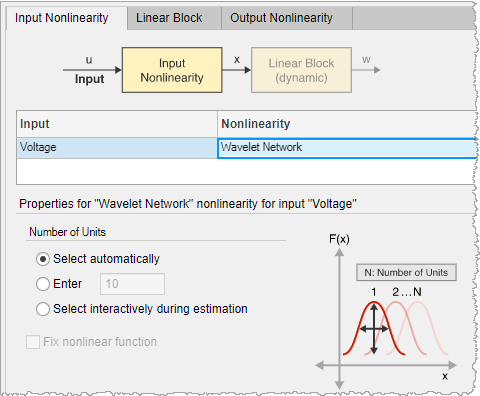
在估计 Hammerstein-Wiener 模型对话框中,选择模型结构选项卡,然后选择输入非线性选项卡。
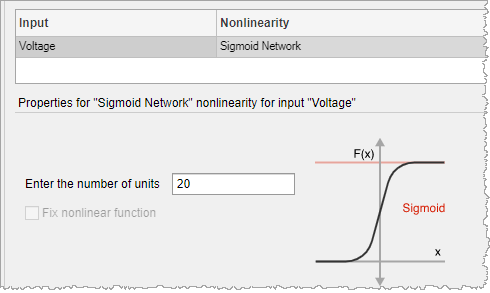
单击电压变量的非线性单元格,然后从列表中选择 Sigmoid 网络。
3.在输入单位数中,将值设置为 20。
4.单击估计。
此操作将模型 nlhw3 添加到系统标识应用程序。 它还会更新模型输出窗口,如下图所示。
5.在估计 Hammerstein-Wiener 模型对话框中,选择输入非线性选项卡。
6.对于电压输入,将非线性设置为小波网络。 单位数的默认值是自动选择。
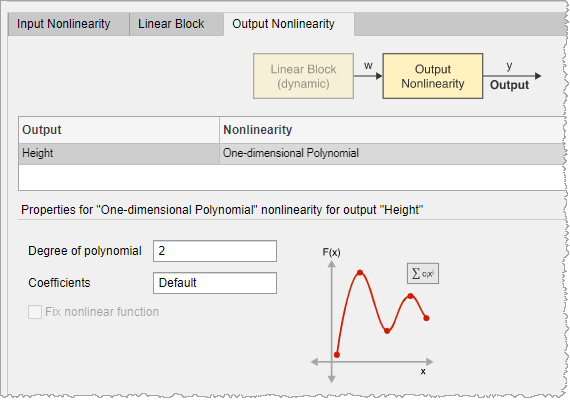
7.选择输出非线性选项卡。
8.将高度输出非线性设置为一维多项式。 将多项式的次数设置为 2。
9.单击估计。
此操作将模型 nlhw4 添加到系统标识应用程序。 它还会更新模型输出窗口,如下图所示。
选择最佳模型
最好的模型是准确描述动力学的最简单的模型。
在此示例中,模型 nlhw3 和 nlhw4 是很好的候选者。