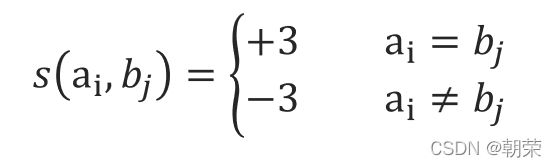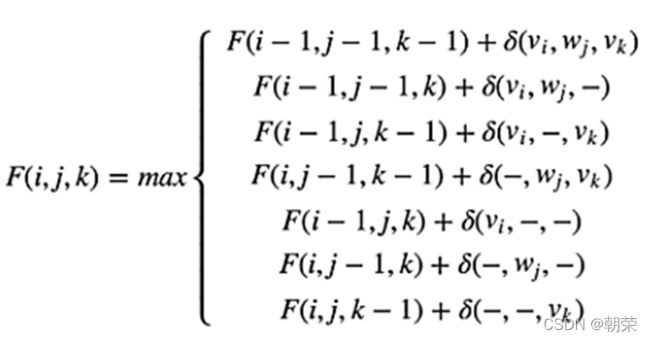【生信】生物序列比对

【生信】生物序列比对

文章的文字与图片全部/部分来源网络或学术论文，文章会持续修缮更新，仅供大家学习使用。

目录

【生信】生物序列比对

1、生物序列比对介绍

2、序列比对算法

基于全局匹配的算法

（1）打分矩阵

（2）动态规划算法

 （3）Needleman-Wunsch算法

基于局部匹配的算法

Needleman-Wunsch算法

Smith-Waterman算法

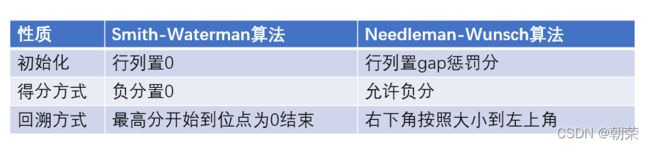
Smith-Waterman算法与Needleman-Wunsch算法的区别

启发式搜索算法

BWT（(Burrows–Wheeler_transform)）算法

3、多序列比对介绍

---

1、生物序列比对介绍

序列比对：是生物信息学的基本组成和重要基础。序列比对是基于生物学中序列决定结构，结构决定功能的普遍规律，将核酸序列和蛋白质一级结构上的序列都看成由基本字符组成的字符串，检测序列之间的相似性，发现生物序列中的功能、结构和进化的信息。

技术手段：两个或者多个序列按照碱基排列进行比较，从而反映片段之间的相似性和阐明序列的同源性。在比对中，错配与突变相应，而空位与插入或缺失对应。

序列比对分类：

1)双序列比对：在生物信息处理中，找出两条序列S和T之间具有的某种相似性关系，这种寻找生物序列相似性关系的算法就是双序列比对算法。通常利用两个序列之间的字符差异来测定序列之间的相似性，两条序列中相应位置的字符如果差异大，那么序列的相似性低，反之，序列的相似性就高。

2)多序列比对：多序列比对是双序列比对的扩展。把两个以上字符序列对齐，逐列比较其字符的异同，使得每一列字符尽可能一致，以发现其共同的结构特征的方法称为多序列比对。

多序列比对的目标是使得参与比对的序列中有尽可能多的列具有相同的字符（即使得相同残基的位点位于同一列）。发现不同的序列之间的相似部分，从而推断它们在结构和功能上的相似关系，主要用于分子进化关系，预测蛋白质的二级结构和三级结构、估计蛋白质折叠类型的总数，基因组序列分析等。

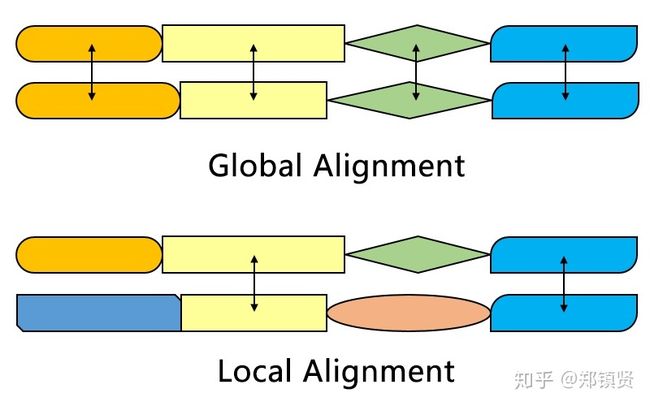
3)全局比对：是指将参与比对的两条序列里面的所有字符进行比对。全局比对主要被用来寻找关系密切的序列。

4)局部比对：通过较少的改动便可以用来识别匹配的子序列， 并且忽略匹配区域之前或之后的失配和空位;局部比对时，表中小于零的位置用零代替。主要用来考察两序列的某些特殊片段。

序列比对算法：

1. 基于全局匹配的算法：动态规划算法、Needleman-Wunsch算法
2. 基于局部匹配的算法： Smith-Waterman算法
3. 启发式搜索算法：BWT算法和BLAST算法

解决的问题：用于研究由共同祖先进化而来的序列，特别是如蛋白质序列或DNA序列等生物序列。序列比对还可用于语言进化或文本间相似性之类的研究。

序列相似性—>序列同源性：

序列相似性：序列之间的相似程度是可以量化的参数。

序列同源性：序列是否同源需要有进化事实的验证。

如果两个序列之间具有足够的相似性，就推测二者可能有共同的进化祖先，经过序列内残基的替换、残基或序列片段的缺失、以及序列重组等遗传变异过程分别演化而来。

如果两个序列有显著的保守性，要确定二者具有共同的进化历史，进而认为二者有近似的结构和功能还需要更多实验和信息的支持。

通过大量实验和序列比对的分析，一般认为蛋白质的结构和功能比序列具有更大的保守性，因此粗略的说，如果序列之间的相似性超过30%，它们就很可能是同源的。

序列相似性—>结构相似—>功能相似：

由中心法则可以知道DNA序列转录产生RNA序列，进而翻译成蛋白序列，序列之间的差异性将会导致传递信息的差异，导致下游生物学功能的差异性，如蛋白质结构的差异，酶活性的差异等。

2、序列比对算法

基于全局匹配的算法

（1）打分矩阵

对于两种相似的序列，DNA复制一共有三种情况可能导致两个序列不同：

1. SNP单核苷酸多态性，简单说就是碱基的替换，这是出现频率最高的，比如把AGCT复制成了AGCC
2. INSERT, 就是多复制了一个，比如吧AGCT复制成了AAGCT
3. DELETION，就是少复制了，比如吧AGCT复制成了AGC

那么两个序列对应的存在可能性一共有三种：

1. MATCH：上下匹配
2. MISMATCH：出现了SNP，上下不匹配
3. GAP：出现了Indel（insertion和deletion，导致两个序列有一个出现了空缺

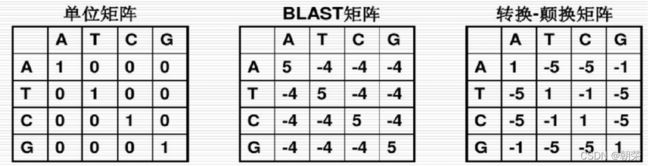
 打分矩阵(Scoring Matrix)：用于计算序列相似性(Similarity)，其数学本质是统计权重，可以处理序列不确定性的问题。

判断序列相似性，在统计上来说即为计算序列间的距离。最简单的距离是编辑距离。但这种距离不能反映与实际核酸序列和蛋白质序列进化的复杂性，因而需要考虑到权重的距离计算方法，即打分矩阵。给不同的序列匹配定义的一系列相似性分值，用来计算两条序列间的相似性。计算相似性时，DNA考虑了序列保守性突变，蛋白质考虑了氨基酸的相似性，这要比一致性这一个指标更具有生物学意义。

等价矩阵：相同为1，不相同为0。

转换-颠换矩阵：在进化过程中，转换的发生频率远比颠换高，此矩阵正好反映了此情况。转换为-1，颠换为-5。

BLAST矩阵：两个核苷酸相同，得分为+5，不同则为-4。

（2）动态规划算法

可以参考博主前面写的这篇博客，《3、基因组组装——动态规划算法》部分。

梦里是碗妹的博客_CSDN博客-数据结构与算法,生物信息学,操作系统领域博主

在这里再用一个例子进行阐述：

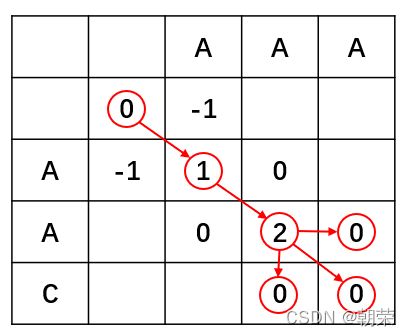
第一步，绘制比对矩阵，这里比对序列为“AAA”和“AAC”，需要声明的是第二行和第二列空着的位置表示gap。

第二步，填写矩阵，第一个网格位置的值无意义得分为零。每一个位置得到的打分的公式(需要注意的是这里表示列，j表示行)，网格中每个位置的得分都等于等号右边3个式子中的最大值。(Xi aligned to Yi)表示此位置的两个碱基正好对上。若为下面两个式子则表示碱基对上一个空位 (gap)。通过打分的公式我们一步一步往前推进，并保留最大值对应的前进路径，如果不同的路径对应相同的最大值，则保留多个路径。

 第三步，根据路径回溯结果。

 （3）Needleman-Wunsch算法

Needleman-Wunsch这个算法也是基于动态规划算法原理设计的，原理和动态规划相似。

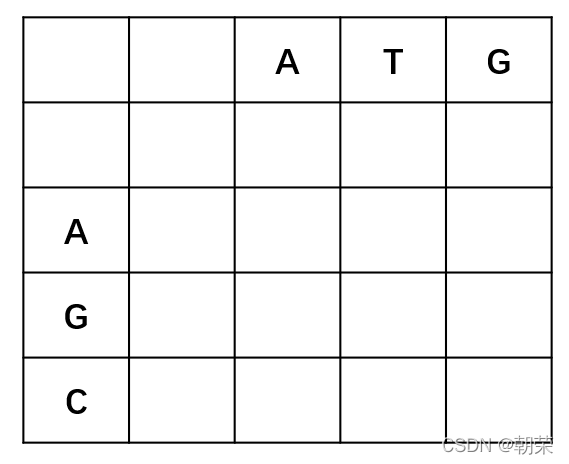
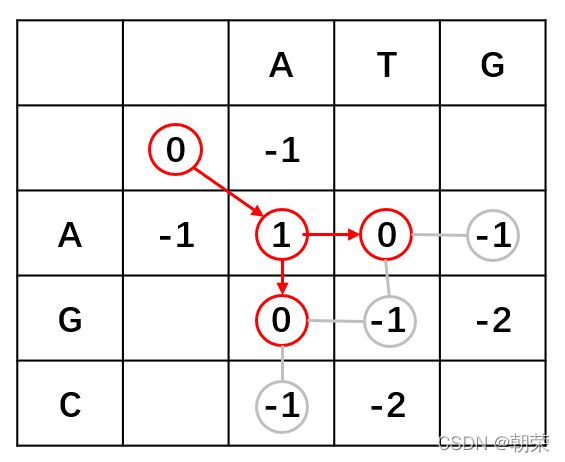
第一步，绘制比对矩阵，这里比对序列为“ATG”和“AGC”，需要声明的是第二行和第二列空着的位置表示gap。

 

第二步，补充矩阵，第一个网格位置的值无意义得分为零。每一个位置得到的打分的公式(需要注意的是这里表示列，表示行)，网格中每个位置的得分都等于等号右边3个式子中的最大值。(Xi aligned to Yi)表示此位置的两个碱基正好对上。若为下面两个式子则表示减基对上一个空位(gap)。通过打分的公式我们一步一步往前推进，并保留最大值对应的前进路径，如果不同的路径对应相同的最大值，则保留多个路径。

第三步，打分之后，从得分最高的元素开始根据得分的来源回溯至上一位置，如此反复直至遇到得分为O的元素

对于序列“GCATGCU”和“GATTACA”进行比对：

 第一步，构建得分矩阵，矩阵的行列分别是两个序列的碱基排列，第一行和第一列为惩罚得分，按照0，-1，-2依次排列，因为相邻两位之间的当成一次GAP.，得到的矩阵如下所示：

然后从左上到右下的顺序计算每个位点的得分，每个位点的得分是与它位置的上面，左边和左上角三个位置的得分相关。具体计算如下：

总体每个位点的得分为：

三个方向的得分=该方向上一位点得分+移动过程得分

最后选取三个方向最高得分作为该位点的得分，以此循环从上到下，从左到右得到整个矩阵的得分。最后的得分如下：

最右下角的得分肯定是最优得分，因为它是从每种子情况的最优得分得到的。但是我们还需要知道它是从哪一条路径得到的这个最优得分。因此需要回溯，回溯的方式就是看每个回溯位点的左上方，上方和左方最大值位置，最后就可以得到整个回溯路径：

 为了得到最后的比对序列，从右下方开始，如果最大值出现在上面，则横向这条序列引入一个GAP ("-")，纵向这条序列取该处碱基；如果最大值出现在左边，则纵向这条序列引入一个GAP ("-")，横向这条序列取该处碱基; 如果最大值出现在左上角，则不引入GAP，纵向和横向均取该处碱基。这样获取到两段序列，最后反转过来，即为最终结果。当然这个回溯的路径不一定唯一，当三个位置有两个相同的时候，两个路径都是可行的，比如按照上图中红蓝两种走法就会出现两种情况：如下所示：

U → CU → GCU → -GCU → T-GCU → AT-GCU → CAT-GCU → GCAT-GCU
A → CA → ACA → TACA → TTACA → ATTACA → -ATTACA → G-ATTACA
             ↓
    (branch) → TGCU → ...
             → TACA → ...

 最后按照上面，我们可以得到三个比对得分都为0的比对结果：

序列          最佳匹配
---------    ----------------------
GCATGCU      GCATG-CU      GCA-TGCU      GCAT-GCU
GATTACA      G-ATTACA      G-ATTACA      G-ATTACA

基于局部匹配的算法

Needleman-Wunsch算法

 

  

Smith-Waterman算法

（参考从零开始生物信息学(3):序列比对-Smith–Waterman算法 - 知乎 (zhihu.com)）

基于Needleman-Wunsch算法扩展得到的Smith-Waterman算法，这是一个基于局部匹配的动态规划算法，后来常用的序列比对算法例如fasta和blast也是基于这个算法改进的。

以序列“TGTTACGG”和“GGTTGACTA”进行比对为例：

定义得分公式如下：

如果两个位点的碱基匹配（MATCH），得3分，出现不匹配(MISMATCH)或者为-3分。并且如果出现空缺（GAP）惩罚分数做一个线性增长惩罚：Wk = 2k (k指的是出现GAP的次数，初始值为2，也就是每次出现一个GAP惩罚的分数依次为-2，-4，-6，递增)。

和Needleman-Wunsch算法相似，我们也需要构造一个得分矩阵用于Smith-Waterman算法的比对序列回溯，矩阵的行列同样是是两个序列的碱基排列，第一行和第一列为置0，这是和Needleman-Wunsch算法不同的地方。

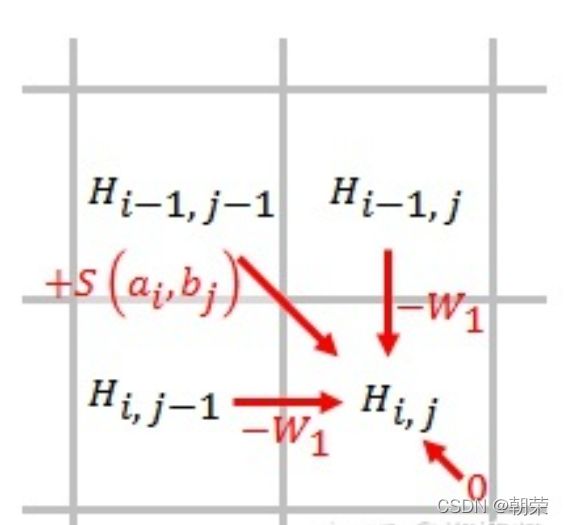
然后同样地从左上到右下的顺序计算每个位点的得分，每个位点的得分是与它位置的上面，左边和左上角三个位置的得分相关。最后取三者的最大值，具体计算如下：

 

其中s(ai, bj)函数就是我们上面定义的匹配或者不匹配两种情况，W是横方向或者纵方向的GAP惩罚。最后计算得分方式如下：

三个方向的得分=该方向上一位点得分+移动过程得分

总得分=max(三个方向的得分，0)

为啥要和0比较呢，可以认为就是这里的得分为负了，起到一个重置的作用，以此循环从上到下，从左到右得到整个矩阵的得分。

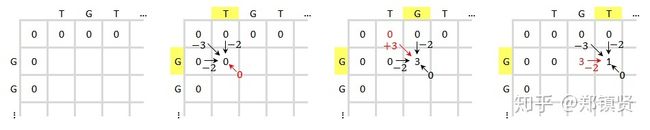
例如，第三个图的对应位置的左上角为0分，但是对应横方向和纵方向的G是匹配的，所以斜方向得分为0+3，横竖两个W都是0-2=-2，所以总的得分就是max(3，-2，-2, 0)=3.其他的依次类推，最后得到整个惩罚矩阵：

 红色箭头是每个位点最高值的来源，然后我们可以发现整个数组有个最大值（蓝色标记），我们需要从最大值处回溯得到整个比对序列。同样的，从矩阵的最大值开始，比较每个当前位点的左上，上方和左方三个方向，如果最大值出现在上面，则横向这条序列引入一个GAP ("-")，纵向这条序列取该处碱基；如果最大值出现在左边，则纵向这条序列引入一个GAP ("-")，横向这条序列取该处碱基; 如果最大值出现在左上角，则不引入GAP，纵向和横向均取该处碱基。值得注意的是，回溯的过程在回溯的值为0就停止，最后将整个序列翻转，就可以得到最终的序列比对结果。

 最终的局部序列比对结果如下：

G T T - A C
| | |   | |
G T T G A C

Smith-Waterman算法与Needleman-Wunsch算法的区别

Smith-Waterman算法针对的序列的局部匹配性。Needleman-Wunsch算法针对的序列的全局匹配性。

对于两段序列而言，即使他们的不相关，或者不具备相似性，他们依旧可以拥有相似的局部序列分布，并且这个局部序列矩阵得分会高于全局的矩阵得分（从矩阵的最大值不是最右下角的值就可以看出），如果我们能在他们之间比对出一些局部片段，具有高度的相似性，一定程度上，我们可以得到两个序列具备同源性，也就是可能拥有相同的祖先，对于一些外显子序列，有可能这些片段会转录出一些相似的RNA及蛋白质。还有就是这种比对方法可会揭示一些匹配的序列段，而本来这些序列段是被一些完全不相关的残基所淹没。

因此，局部比对的相似性往往比全局比对相似性更具有价值。

启发式搜索算法

BWT（(Burrows–Wheeler_transform)）算法

BWT算法可以分为编码和解码两部分。编码后，原始字符串中的相似字符会处在比较相邻的位置；解码就是将编码后的字符串重新恢复成原始字符串的过程。BWT的一个特点就是经过编码后的字符串可以完全恢复成原始字符串。

Mapping ：侧重于把序列放到正确的位置，而不管这个序列的一致性。

Alignment ：是主要让序列和参考序列尽可能的配对，而不管位置。
目前来看，大多数工具都是想既能找到正确的位置，也保证有足够多的Alignment，不过明白这两者的区别对于不同项目的分析非常重要。比如说变异检测就要优先保证联配，而RNA-Seq则要尽可能保证把reads放到正确的位置

BWT编码压缩步骤如下：

1. 首先对要转换的字符串，添加一个不在字符串里的ASCII码表里最小的字符。
2. 对字符串进行依次循环移位，得到一系列的字符串，如果字符串长度为 n， 就可以得到n个字符串，如下面图里的第二列所示。
3. 对2中的位移后的一系列的字符串按照ASCII进行排序，如下图的第四列所示，第三列是排序后的字符串的原index位置。
4. 取位移后的一系列字符串的首字母出来作为 F 列， 最后一个字母作为 L 列。如下图 F 列 和L 列所示。
5. L 列就是最后的编码结果。

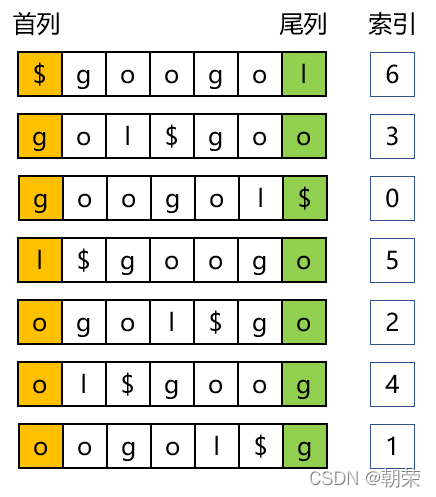
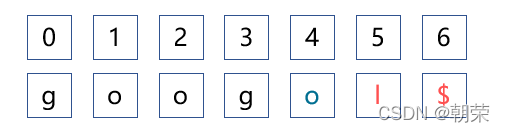
对已知序列“googol”字符串构建索引

第一步，转换成字符串数组

 第二步，按字典顺序（ASCII）进行排序，首字母相同则看第二列字母。

 第三步，还原原字符串

尾列=“lo$oogg"，首列=“$gglooo”，尾列字符串的第一个元素“l”是原字符串“googol”中最后一个元素，同一行中，最后一个元素都是第一个元素的上一个元素。 

还原字符串的方式：排序过程中$始终在第一行，且尾列I是$的上一个元素，所以我们可以填写出最后两个字符。l对应的索引是5，找到5所在的行，可以发现首列就是字符l，尾列o为l的上一个字符，填入o到I的前一个位置。

 第四步，判断“oog”是否是“googol”的子字符串，在什么位置。

BWT算法是从后往前查找，所以找“oog”这段序列，我们需要先找“g”字符串，由左侧的索引可以发现，“g”对应了两个索引3，0，所以我们分别构建两个初始的可能，分别在索引3和0处填入。索引3的首列是“g”，尾列是“o”，符合条件，按照查询算法继续查询，发现g -> O-> o符合字串规则，所以这个结果是符合条件的，它是字串，且最后一个o所在的对应的索引是1，所以是在原字符串第二个位置匹配上的。索引0的首列是“g”，尾列是“$”，不符合规则。

3、多序列比对介绍

理论上动态规划算法可以推广到多序列比对，在三条序列比对过程中，打分公式如下，会变得更加复杂，可走的路径也更加多变。