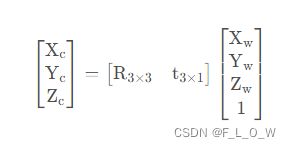三维重建基础： 坐标系 (更新中)

概述

世界坐标系与相机坐标系之间存在着互逆的转换。
具体有：


对某个三维点的坐标进行变换：

• 世界坐标系到相机坐标系： W2C （我们俗称的相机pose，colmap默认输出）
• 相机坐标系到世界坐标系： C2W

---

---

左右手坐标系的xyz通过拇指、食指、中指三者的组合来确定。

参考链接

---

目标是，三维坐标转换至屏幕上的像素坐标。

我们假定起初的三维坐标是在世界坐标系下，那么为了获得其在像片上的对应坐标，我们首先需要做的事情是将三维点的坐标先从世界坐标系转换至相机坐标系下。然后我们再根据摄像机空间中的点坐标，将其投影至像平面上就可以了。
声明：部分图片摘自李博博客：https://ethanli.blog.csdn.net/article/details/113248118，本文主要用于个人笔记，若侵则删。

---

计算机视觉：投影矩阵M： 世界坐标系 -> 像平面坐标系

简写为：

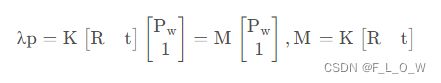
如上式所示，K[R t]可以简写为M矩阵，即投影矩阵，是一个 $3\ast 4$的矩阵，是内参矩阵和外参矩阵的乘积。
通常来说，投影矩阵 $M$也往往会被称之为 $P$。

相机坐标系 -> 像平面坐标系：

世界坐标系 -> 相机坐标系

计算机图形：MVP变换

本小结先主要关注view/camera变换，即相机坐标系和世界坐标系之间的变换。

view/camera 变换

首先定义$e$、$g$、$t$：

一个非常简单的观察就是，如果相机和物体都进行移动的话（保持相机中心和物体的相对关系持续一致），那么我们拍摄的图像理论上是不变的咯。
那么我们就可以考虑把相机先移动到世界坐标系的原点上，然后再旋转对应的轴，使得其能够世界坐标系重合上，然后我们把物体也做一样的变换，就可以保持其与相机的相对关系不变。【需要进一步地解释】
小结一下，变换过程总共可以分为两步：

1. 将相机平移到原点；
2. 将相机旋转到理想状态。
   

平移矩阵很简单，直接就是：

我们考虑旋转矩阵的逆矩阵（描述了世界坐标系到相机坐标系的旋转过程）：

现在我们考虑世界坐标系下$x$轴的基向量为$[1,0,0,0{]}^T$，其进行旋转后，理应变成 $[x_{\hat{g}\times \hat{t}},y_{\hat{g}\times \hat{t}},z_{\hat{g}\times \hat{t}}]$， 即，有：

带入后进行解算，有：

参考链接

在games101_lecture_04中的描述为：

参考slides

常见坐标系定义

参考：https://zhuanlan.zhihu.com/p/593204605?utm_source=zhihu

colmap中的坐标系

colmap坐标系默认输出的是W2C的矩阵，如果想要进行正确的可视化，那么就需要将其变换到世界坐标系下：

https://blog.csdn.net/weixin_44120025/article/details/124604229

线性代数相关基础

几何角度理解线性代数（1）：向量、线性组合、矩阵乘法、行列式
几何角度理解线性代数（2）: 逆矩阵、列空间与零空间

几何角度理解线性代数（3）：点积与叉积

Q & A

• 问：为什么有些旋转矩阵换轴的时候更换列向量，而有些是换行
  答： 以C2W为例，更换列向量是换的Camera坐标系，更换行向量是换的World坐标系。

待办

1. C++中的using是什么作用的？
2. 如何理解dll导出的宏定义？
3. 怎么理解 inline Camera() = default; ?
4. std::move()