定义问题以及用QUBO表示约束
定义问题以及用QUBO表示约束
D-Wave擅长解决的问题之一就是二值优化(optimization of binary variables)问题。二值变量只有变量 0(NO, or FALSE)和变量 1(YES, or TRUE)。
传统计算机可以被认为是由逻辑门(logic gates)组成的,逻辑门是一种简单的决策装置,其根据输入产生输出。虽然 D-Wave 系统并不是基于门的,但巧合的是一个特殊的门(异或门)形成了系统要解决的第一个优化问题。
异或门内容如下:
假设由两个二值的输入 a , b a,b a,b 。若 a = 0 且 b = 0 a=0 且b=0 a=0且b=0,则输出为 1 1 1, 若 a = 1 且 b = 1 a=1 且b=1 a=1且b=1,则输出为 1 1 1, 其他情况下输出为0.
定义目标函数
对于一个有两个qubit的问题,我们希望在退火之后的 qubits 得到一样的值。qubit 的状态有4种情况,如下表所示:
| q 0 q_0 q0 | q 1 q_1 q1 |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
我们需要定义一个目标函数,使其最终实现状态(0,0)和(1,1)。在目标函数中,qubit 是变量。bias(qubit 偏置) 和 strengths(couplers 的强度)是线性项和二次项上的系数。两个 qubit 问题的目标函数有三个项。目标函数的形式如下:
f ( s ) = a 1 q 1 + a 2 q 2 + b 1 , 2 q 1 q 2 (5.1) f(s) = a_1 q_1 + a_2 q_2 + b_{1,2} q_1 q_2 \tag{5.1} f(s)=a1q1+a2q2+b1,2q1q2(5.1)
其中 s s s 是变量 q = [ q 1 , q 2 ] q=[q_1,q_2] q=[q1,q2] 的向量, a 1 a_1 a1和$ a_2$ 是 qubit biases, b 1 , 2 b_{1,2} b1,2 是 coupler 的权重(strengths)。
设置满足最初目标的 a 1 , a 2 , b 1 , 2 a_1,a_2,b_{1,2} a1,a2,b1,2。首先可以看到,当 q 1 q_1 q1 和 q 2 q_2 q2 都等于0(记为(0,0))时,目标函数的值为0,也没有其他可调参数。这就是我们希望得到的状态,对应于基态的最小能量应该为0。同时不希望有状态(0,1)和(1,0)。一种办法就是给 a 1 , a 2 a_1,a_2 a1,a2 两个 biases 都设置为 0.1:
| q 0 q_0 q0 | q 1 q_1 q1 | Objective Value |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0.1 |
| 1 | 0 | 0.1 |
| 1 | 1 | 0.2 + b 1 , 2 b_{1,2} b1,2 |
又因为状态(1,1)也是我们希望得到的状态,一种方式就是给coupler权重设置 b 1 , 2 = − 0.2 b_{1,2}=-0.2 b1,2=−0.2 .最终的目标函数是:
f ( s ) = 0.1 q 1 + 0.1 q 2 − 0.2 q 1 q 2 (5.2) f(s)=0.1q_1 + 0.1q_2 - 0.2q_1q_2 \tag{5.2} f(s)=0.1q1+0.1q2−0.2q1q2(5.2)
上述表格的输出就变成如下所示:
| q 0 q_0 q0 | q 1 q_1 q1 | Objective Value |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0.1 |
| 1 | 0 | 0.1 |
| 1 | 1 | 0 |
当我们对这个问题在D-Wave系统上运行了很多次退火之后(也称为 采样(samples) or 读取(reads)),我们希望得到基态(0,0)和(1,1),而不是激发态(0,1)和(1,0)。
把这个问题在D-Wave2000Q系统上运行1000次之后,可以获得1000个采样结果。
| Energy | State | Occurrences |
|---|---|---|
| 0 | (0,0) | 555 |
| 0 | (1,1) | 443 |
| 0.1 | (0,1) | 1 |
| 0,1 | (1,0) | 1 |
如果再次运行这个问题,我们期望得到的 energy 0 可能会有不同,但是一定是在500的附近(样本的50%左右)。
需要注意的是,结果中大多数情况是(0,0)和(1,1),调用足够多次QPU时,会看到偶尔的(0,1)和(1,0)这样的解。对于更复杂的 QUBOs ,这种反复求解同一个问题以获得一系列答案的过程称为采样(sampling)。
问题缩放(Problem Scaling)
考虑另外一个 2-qubit 问题,这次给 qubit biases 和 coupler strength 分别赋值0.5和1,目标函数如下:
f ( s ) = 0.5 q 1 + 0.5 q 2 − q 1 q 2 (5.3) f(s) = 0.5q_1 + 0.5q_2 - q_1q_2 \tag{5.3} f(s)=0.5q1+0.5q2−q1q2(5.3)
同上,可以得到如下结果:
| q 0 q_0 q0 | q 1 q_1 q1 | Objective Value |
|---|---|---|
| 0 | 0 | 0.5 |
| 0 | 1 | 0.5 |
| 1 | 0 | 0.5 |
| 1 | 1 | 0 |
因为这个问题的激发态和前面那个问题中的值不同,导致基态和激发态之间的能量差更大(0.5 和 0.1),所以这次可能会看到不同的结果。话句话说,当基态和激发态之间存在较大的间隙(能量差)时,从基态更不容易达到激发态。
前面在第一个问题中,我们在返回的结果中可以看到了一小部分激发态。如果我们多次运行这两个问题,通常会观察到相同的结果,但实际是第二个问题(明显)存在较大差距,这与我们的预期的50%差别有点大。
这一结果是由D-Wave系统的一个称为**自动缩放(auto-scaling)**的功能引起的。每个QPU的偏差 a a a 和强度 b b b 都有一个允许的范围值。除非我们明确禁用自动缩放,否则D-Wave软件会调整问题的 a a a 和 b b b 的值,使得把问题发送到QPU之前采用整个可用的(a,b)范围。因此,在运行这两个问题时,它们向QPU呈现相同的(a,b)值,因此返回的解决方案实际上是相同的。当在运行结束返回能量值和目标值时,我们使用的是预缩放(pre-scaling)值。
下面来测试一下这个功能。首先运行第一个问题1000次(激发态的值是 0.1),禁用 auto-scaling。这次看到的结果如下所示:
| Energy | State | Occurrences |
|---|---|---|
| 0 | (0,0) | 272 |
| 0 | (1,1) | 526 |
| 0.1 | (0,1) | 124 |
| 0.1 | (1,0) | 68 |
然后运行第二个问题1000次(激发态的值是 0.5),禁用 auto-scaling。这次看到的结果如下所示:
| Energy | State | Occurrences |
|---|---|---|
| 0 | (0,0) | 436 |
| 0 | (1,1) | 563 |
| 0.5 | (0,1) | 1 |
| 0.5 | (1,0) | 0 |
这些结果表明,在没有自动缩放(auto-scaling)的情况下,第一个问题比第二个问题具有更小的间隙(基态和激发态的能量差),并且返回更多的激发态样本。间隙越小,从基态变到激发态越容易(激发态的次数越多)。
用 QUBO 来表示约束
先用 QUBOs 定义一个简单的约束(constraints),可以拓展到更大更复杂的问题中。
exactly-one-true 约束是一个布尔(Boolean)可满足性(satisfiability)问题,给定一组变量,我们想知道何时恰好有一个变量为1(真)。
例如,当优化一个旅行销售人员通过一系列城市的路线时(TSP),需要一个约束条件,必须强制销售人员在旅行的每个阶段只能在一个地方(exactly one city),同时在多个地方是无效的。
下面就来说明一下如何以D-Wave可以解决的方式来构建一个简单的 exactly-one-true。步骤如下:
- 从目标函数开始:在这个例子中,就是从有三个变量的 exactly-one-true 约束开始,然后建立一个满足这个目标的真值表。
- 建立一个能够得到所期望的状态且抑制其他状态的 QUBO。
- 把 QUBO 转换到一个graph中。
对目标函数建真值表
考虑一个简单的例子:给定三个变量 a , b , c a,b,c a,b,c ,我们想知道什么时候恰好只有一个变量是1。(也就是说, a , b , c a,b,c a,b,c 中只有一个变量是1,而其他两个变量是0),真值表表示如下:
| a a a | b b b | c c c | Exactly 1 |
|---|---|---|---|
| 0 | 0 | 0 | FALSE |
| 1 | 0 | 0 | TRUE |
| 0 | 1 | 0 | TRUE |
| 1 | 1 | 0 | FALSE |
| 0 | 0 | 1 | TRUE |
| 1 | 0 | 1 | FALSE |
| 0 | 1 | 1 | FALSE |
| 1 | 1 | 1 | FALSE |
建立一个只有一个为真的 QUBO
我们希望找到一个函数 E ( a , b , c ) E(a,b,c) E(a,b,c) ,当这个目标为真时,使得函数是最小的,可以用下式表示:
a + b + c = 1 a + b + c = 1 a+b+c=1
或
a + b + c − 1 = 0 a + b + c - 1 = 0 a+b+c−1=0
上述第二个式子表示的含义是,当 a , b , c a,b,c a,b,c 都为0时,结果时 -1, 这是一个比 TRUE 状态更低的能量状态。避免这个情况出现的方式是,给这个方程加平方:
( a + b + c − 1 ) 2 (a + b + c - 1 )^2 (a+b+c−1)2
于是就有平方表达式:
E ( a , b , c ) = ( a + b + c − 1 ) 2 E(a,b,c) = (a + b + c - 1)^2 E(a,b,c)=(a+b+c−1)2
因为这些变量都是二值的(0 和 1),有 a 2 = a a^2 = a a2=a于。是我们的目标函数就变成了
E ( a , b , c ) = 2 a b + 2 a c + 2 b c − a − b − c + 1 E(a,b,c) = 2ab + 2ac + 2bc - a - b - c + 1 E(a,b,c)=2ab+2ac+2bc−a−b−c+1
其中函数 E ( a , b , c ) E(a,b,c) E(a,b,c) 的能量(energy)就是目标函数的值。
加入 energy 这一列之后再看一下真值表。需要注意的是,最低能态和 exactly-one-true 约束是匹配的。解越好,能量越低。
| a a a | b b b | c c c | Exactly 1 | Energy |
|---|---|---|---|---|
| 0 | 0 | 0 | FALSE | 1 |
| 1 | 0 | 0 | TRUE | 0 |
| 0 | 1 | 0 | TRUE | 0 |
| 1 | 1 | 0 | FALSE | 1 |
| 0 | 0 | 1 | TRUE | 0 |
| 1 | 0 | 1 | FALSE | 1 |
| 0 | 1 | 1 | FALSE | 1 |
| 1 | 1 | 1 | FALSE | 4 |
表达为 QUBO 的形式则为:
E ( x 0 , x 1 , x 2 ) = 2 x 0 x 1 + 2 x 0 x 2 + 2 x 1 x 2 − x 0 − x 1 − x 2 + 1 E(x_0,x_1,x_2) = 2x_0x_1 + 2x_0x_2 + 2x_1x_2 - x_0 - x_1 -x_2 + 1 E(x0,x1,x2)=2x0x1+2x0x2+2x1x2−x0−x1−x2+1
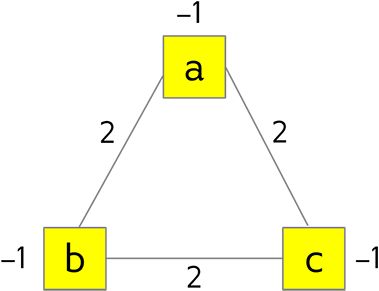
把 QUBO 转换到 Graph 中
QUBO 能量函数能用三角图表示如图6.2。每个二值变量都是一个带有线性系数的 bias 节点。每个二次项都变成节点之间的一条 edge。